Les seuls cycles possibles en géométrie elliptique sont les cercles puisqu’il n’y a qu’un seul type de pinceau, à centre.
Le cercle de centre \(O\) passant par \(A\) est le lieu des images (\(symA\) ci-dessous) de \(A\) par toutes les symétries axiales d’axe passant par \(O\). Ayant construit le symétrique d’un point, on peut déjà explorer sur le cercle.
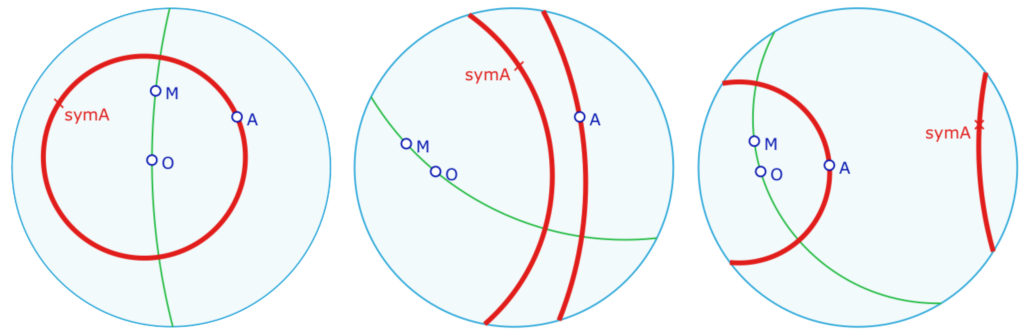
Dans un premier temps, on constate que, dans le modèle du disque de Klein, le cercle elliptique est représenté par un cercle euclidien, ce qui est logique car les cercles sur la sphère ont comme image par projection stéréographique – sauf s’ils passent par le pôle nord bien entendu – un cercle du plan. Résultat qu’il faut néanmoins adapter à l’antipodie elliptique. Cette antipodie ramène le cercle général dans le disque de Klein, et donc le cercle projeté peut se transformer en deux arcs de cercles, avec identification des points opposés sur le cercle unité.
Dans les figures suivantes, on remarquera qu’il y a deux macros : la macro de cercle elliptique bien entendu, mais aussi une donnant le « cercle euclidien support », c’est-à-dire le cercle projeté de la sphère dans le plan euclidien. C’est sur ce cercle que l’on prendra un point pour faire des animations sur les cercles elliptiques.
Intersection de deux cercles – Triangles équilatéraux
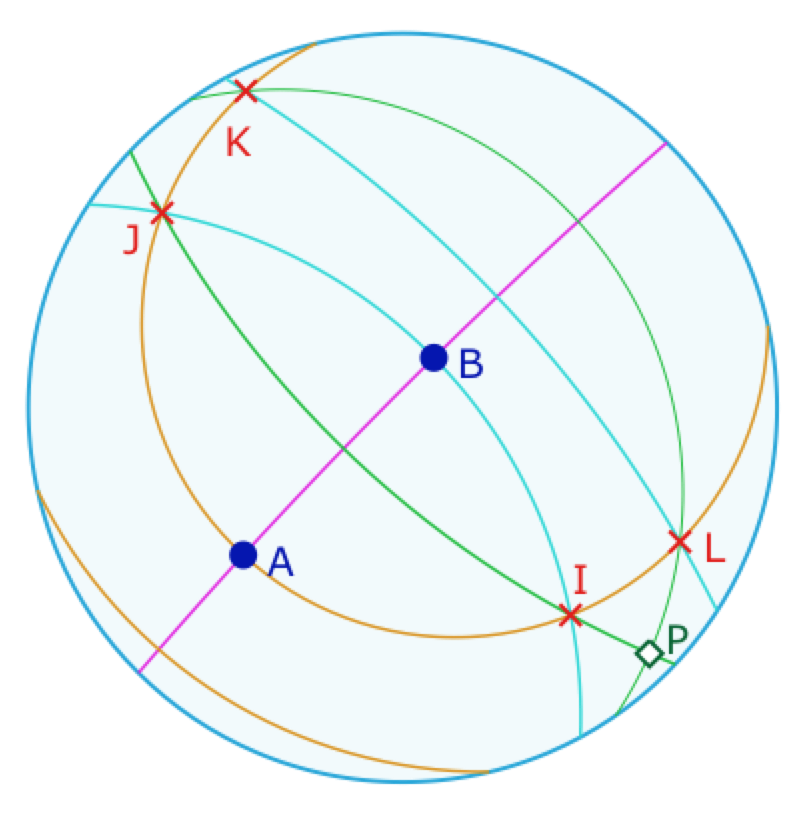
Les cercles de centre \(A\) passant par \(B\) et de centre \(B\) passant par \(A\) peuvent se couper en 4 points \(I, J, K,\) et \(L\).
Pour construire ces 4 intersections de manière optimale, on remarquera qu’elles sont sur les deux médiatrices de \(A\) et \(B\), en vert ci-contre.
Le quadrilatère \(IJKL\) est donc, par construction, un losange de centre \(P\), le pôle de la droite \((AB)\)) et intersection des deux médiatrices de \(A\) et \(B\).
Il y donc jusqu’à 4 triangles équilatéraux de côté AB.
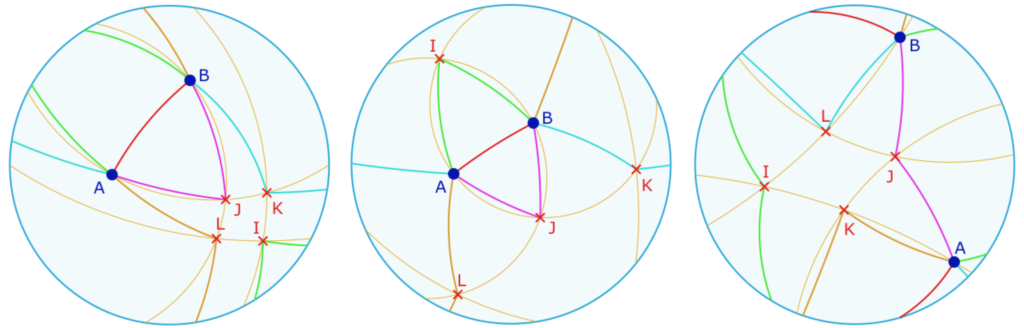
Commencer par manipuler le cercle seul, puis les deux cercles et leurs intersections avant d’afficher les triangles.
Préférer ouvrir cette figure dans un nouvel onglet
Triangle orthique d’un triangle et cercle associé
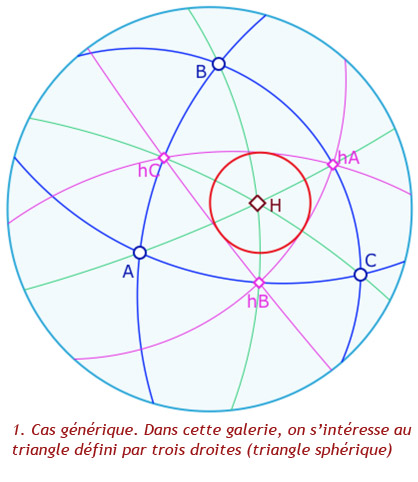
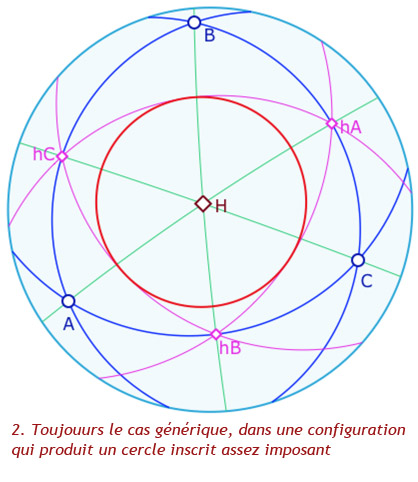
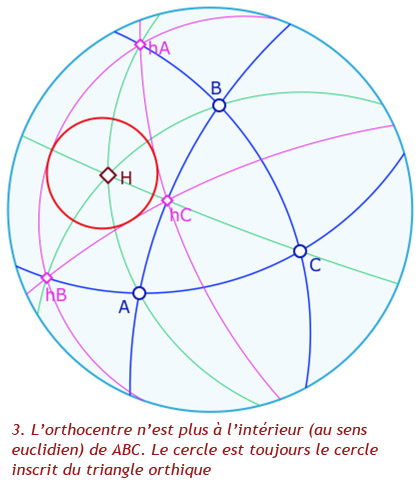
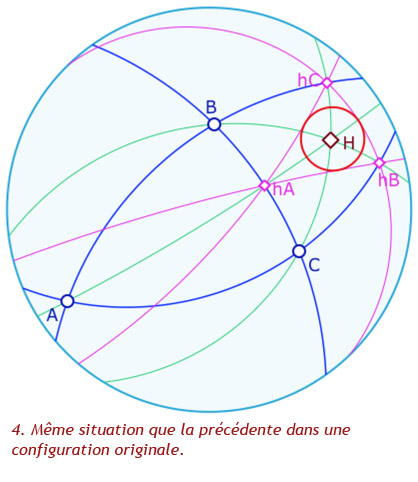
La propriété du triangle orthique est absolue, donc aussi elliptique : l’orthocentre \(H\) est l’intersection de bissectrices de l’orthique du triangle. Voyons déjà cela dans une galerie :
La figure associée
Agir sur les sommets du triangle
Préférer ouvrir cette figure dans un nouvel onglet
Le cas d’un triangle tripolaire
Pour un triangle tripolaire, tout point n’appartenant pas aux trois droites est orthocentre du triangle. Il y a donc une infinité de triangles orthique dont l’intersection des hauteurs est centre du cercle inscrit.
Déplacer \(A, B\) ou \(H\).
Préférer ouvrir cette figure dans un nouvel onglet
Bissectrices et cercles associés
Bissectrices et cercles exinscrits
La bissectrice intérieure d’un angle se construit facilement, comme on l’a fait pour le milieu, en utilisant le fait que le modèle est conforme.
On a déjà dit que, dans le cas absolu très général, les bissectrices d’un trilatère ne sont pas nécessairement en pinceau, sauf dans un cas particulier : celui où deux bissectrices ont un point commun, alors les trois sont en pinceau à centre. Or c’est le cas en géométrie elliptique, puisque deux droites sont toujours sécantes. Donc les bissectrices d’un triangle (trois points, ou trois droites) sont concourantes. Il y a donc bien un cercle inscrit et des cercles exinscrits.

Préférer ouvrir cette figure dans un nouvel onglet
Malfatti du triangle sphérique
Une figure elliptique complète remplirait les autre régions …
Les centres des 4 cercles circonscrits d’un triangle sont aussi les pôles des droites des milieux.
Préférer ouvrir cette figure dans un nouvel onglet