Comme signalé dans les pages précédentes, les divers pinceaux de droites remarquables ont été abordés dans les pages précédentes, sauf celui des médianes. Dans les menus précédents (DP – ELL – PS – PSH), nous avons largement vérifié expérimentalement que les médianes non seulement sont en pinceau, mais aussi sont concourantes(1). Pour montrer ce résultat, Bachmann utilise un autre théorème important (dû à Hessenberg – 1905), sur une notion que nous allons maintenant aborder, l’antiappariement. Mais avant cela commençons par un lemme technique sur les pinceaux.
(1) On a aussi vu, par exemple dans cette page (section « le plan affine d’ordre 3 »), qu’il y a un cas – et on verra ultérieurement que c’est le seul – où les médianes ne sont pas concourantes, c’est le cas euclidien sur un corps de caractéristique 3.
Le lemme des 9 droites
Proposition : on considère 6 isométries \(\alpha_1, \alpha_2, \alpha_3, \beta_1, \beta_2, \beta_3\) telles que
• \(\alpha_1 \neq \alpha_2\) et \(\beta_1 \neq \beta_2\)
• huit des produits deux à deux sont des droites (par exemple sauf \(\alpha_3 \beta_3\)) Alors le neuvième produit, \(\alpha_3 \beta_3\), est aussi une droite.
\hline
\text{ isométries} & \alpha_1 & \alpha_2 & \alpha_3 \\ \hline
\beta_1 & \Delta & \Delta & \Delta \\ \hline
\beta_2 & \Delta & \Delta & \Delta \\ \hline
\beta_3 & \Delta & \Delta \\ \hline
\end{array}\)
Bachmann résume la situation dans ce tableau en disant que si, pour deux groupes de trois isométries (avec les hypothèses de distinction), 8 des 9 cases du tableau sont des droites, la neuvième aussi.
Preuve du lemme : si \(\beta_3 = \beta_1\), le résultat est vrai puisque \(\alpha_3 \beta_1\) est déjà une droite par hypothèse. On se place désormais dans le cas où \(\beta_3 \neq \beta_1\). On peut alors écrire deux séries d’égalités :
\((E_1) \; \; (\alpha_1 \beta_1)^{-1} (\alpha_1 \beta_2) = (\alpha_2 \beta_1)^{-1} (\alpha_2 \beta_2) = (\alpha_3 \beta_1)^{-1} (\alpha_3 \beta_2) = \beta_1^{-1}\beta_2\)
\((E_2) \; \; (\alpha_1 \beta_1)^{-1} (\alpha_1 \beta_3) = (\alpha_2 \beta_1)^{-1} (\alpha_2 \beta_3) = \beta_1^{-1}\beta_3\)
Or par hypothèse, les 8 parenthèses différentes de ces égalités représentent des droites, donc sont égales à leurs inverses, et les produits des parenthèses deux à deux ne sont pas égaux à 1 car \(\alpha_1 \neq \alpha_2\) pour \((E_1)\) et \(\beta_1 \neq \beta_2\) pour \((E_2)\). On peut donc réécrire – avec des notations évidentes – ces égalités sous la forme : \((E_1) \; \; d_1d’_1=d_2d’_2=d_3d’_3\) et \((E_2) \; \; \delta_1 \delta’_1 = \delta_2 \delta’_2\).
Alors, les produits de \((E_1)\) sont ceux du pinceau \(\mathscr{P}_{d_1d’_2}=\mathscr{P}_{d_1d_2}\) puisque \(d_1 \neq d_2\) (par \(\alpha_1 \neq \alpha_2\)). Et comme \(d_1 = \delta_1\) et \(d_2 = \delta_2\), si on considère le pinceau précédent et \(\mathscr{P}_{\delta_1 \delta’_1}\), on a deux droites distinctes, \(d_1 \neq d_2\), dans deux pinceaux, ces pinceaux sont confondus (Th 18) : ainsi ces huit droites sont dans un seul pinceau.
Enfin, avec \(\alpha_3 \beta_3 = (\alpha_3 \beta_1)(\alpha_1 \beta_1)^{-1}(\alpha_1 \beta_3\), comme produit de trois droites en pinceau, \(\alpha_3 \beta_3\) est aussi une droite, qui plus est, du même pinceau.
Le théorème d’antiappariement
Les axiomes de tri-réflexions étant posés et les propriétés des pinceaux établies, il est naturel de s’intéresser à cette relation entre la droite \(c\) d’un pinceau \(\mathscr{P}_{ab}\) et le produit \(d=acb\) du même pinceau. Cette correspondance, Bachmann l’appelle l’antiappariement(2). Il note alors \(c^*\) la droite anti-appariée de \(c\) dans \(\mathscr{P}_{ab}\) ou plus généralement, puisque la relation est symétrique, le couple \((c, c^*)\) de droites antiappariées dans \(\mathscr{P}_{ab}\)).
(2) Gegenpaarung en allemand ou counterpairing en anglais.
Ce vocabulaire « dans \(\mathscr{P}_{ab}\) » (qui signifie qu’il s’agit d’une propriété de pinceau) est justifié par la remarque suivante : si deux droites \(u\) et \(u^*\) sont antiappariées dans \(\mathscr{P}_{ab}\), alors l’antiappariement de \((c, c^*)\) est aussi vrai dans \(\mathscr{P}_{uu^*}\) = \(\mathscr{P}_{ab}\).
En effet, supposons que \(u^*=aub\) et \(c^*=acb\). Alors \(ucu^*=ucaub\). Mais comme les droites \(a, c, u\) sont dans \(\mathscr{P}_{ab}\), \(uca\) est une droite égale à \(auc\) et donc \(ucu^*=acb=c^*\). Ainsi, pour deux couples de droites antiappariées \((u, u^*)\) et \((v, v^*)\) d’un même pinceau, on a toujours \(u^*=vuv^*\), soit en particulier \(uv^*=vu^*\).
On peut alors parler de couple antiapparié à un autre (dans un même pinceau). On dira aussi que \(u^*\) et \(v^*\) sont antiappariées à \(u\) et \(v\) pour un même antiappariement.
Un première conséquence – que l’on mettra en relation avec l’isogonalité – est que si un couple \((u, u^*)\) admet une bissectrice \(b \; (bu^*=ub)\), alors tout couple \((v, v^*)\) anti-apparié à \((u, u^*)\) admet la droite \(b\) comme bissectrice.
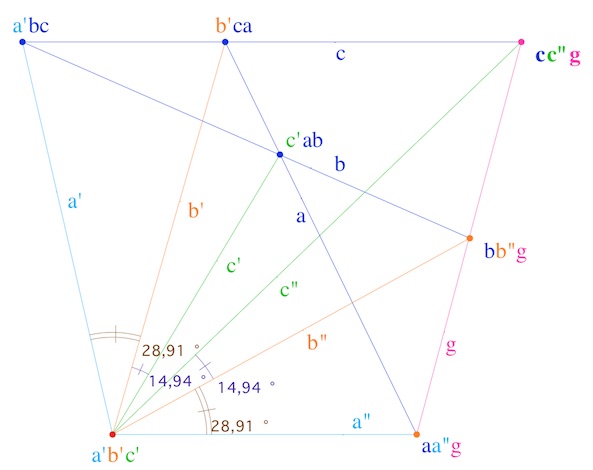
Théorème d’antiappariement
Soient \(a, b, c\) un trilatère, \(a’, b’, c’\) trois droites en pinceau telles que chaque triplet \((a’, b, c)\), \((b’, c, a)\) et \((c’, a, b)\) soient aussi en pinceau, et \(a^{ \prime \prime}\), \(b^{ \prime \prime}, c^{ \prime \prime}\) les antiappariées à \(a’, b’\) et \(c’\) pour un même antiappariement. On suppose de plus que \(a a^{ \prime \prime} \neq b b^{ \prime \prime}\).
Alors toute droite \(g\) en pinceau avec \((a, a^{ \prime \prime})\) et \((b, b^{ \prime \prime})\) le sera aussi avec \((c, c^{ \prime \prime})\).
L’illustration ci-contre, où les points représentent les hypothèses (et la conclusion en rose) sur les pinceaux est proposée par Bachmann comme représentation mnémotechnique du théorème : en particulier on distingue les droites initiales \(a, b, c\) « en trilatère » c’est-à-dire non en faisceau. En général, elles ne sont pas non plus « en triangle » comme ici.
La représentation de Bachmann est plus succincte, avec d’autres notations – et sans couleur – mais avec les égalités d’angles dues aux égalités ci-dessous (et le fait que l’on représente les pinceaux par des points, donc par des pinceaux à centre).
Preuve du théorème : les définitions des antiappariées de \(a’, b’, c’\) pour le pinceau \(\mathscr{P}_{a’b’}\) s’écrivent : \(a’b’= b^{ \prime \prime}c^{ \prime \prime}, \; b’c’ = c^{ \prime \prime}b^{ \prime \prime}\) et \(c’a’ = a^{ \prime \prime}c^{ \prime \prime}\). On peut alors compléter le tableau de produit d’isométries suivant :
\hline
\text{ligne / colonne} & c^{\prime \prime}a’b & c^{\prime \prime}b’a & g \\ \hline
a a^{\prime \prime} & ac’b & (c’a’b’)^a & a a^{\prime \prime}g\\ \hline
b b^{\prime \prime} & (c’b’a’)^b & bc’a & b b^{\prime \prime}g\\ \hline
c c^{\prime \prime} & ca’b & cb’a \\ \hline
\end{array}\)
D’après les hypothèses, les 8 produits d’isométries sont des droites. Vérifions que nous sommes dans les hypothèses du lemme des 9 droites (\(\alpha_1 \neq \alpha_2\) et \(\beta_1 \neq \beta_2\)) : \(a a^{ \prime \prime} \neq b b^{ \prime \prime}\) est une hypothèse du théorème. On ne peut avoir \(c^{\prime \prime}a’b = c^{\prime \prime}b’a\) car alors, on aurait \(a’bc = b’ac\) ce produit appartenant aux deux pinceaux distincts (\(a, b, c\) est un trilatère) \(\mathscr{P}_{bc}\), \(\mathscr{P}_{ac}\), il serait égal à \(c\), ce qui aboutit à \(a’ = a\) et \(b’ = b\), en contradiction avec l’hypothèse que \(ca’b\) soit une droite et \(a, b, c\) un trilatère. Ainsi, on a bien \(c^{\prime \prime}a’b \neq c^{\prime \prime}b’a\). Le lemme des 9 droites est donc applicable, le produit dans la dernière case (\(cc^{\prime \prime}g\)) est une droite et donc \(g\) est aussi en pinceau avec \(c\) et \(c^{\prime \prime}\).
Le pinceau des médianes
Théorème : soit \(ABC\) trois points non alignés, \(I\) et \(J\) des milieux de \((A, B)\) et de \((B,C )\) – soit \(C=B^J\) et \(A=B^I\) – et \(v\) la(3) droite incidente à \(B\) appartenant au pinceau de droites \(\mathscr{P}_{uv}\) en notant \(u=(AJ)\) et \(w=(CI)\).
Alors il existe un point \(K\), incident à \(v\), et tel que \(C^K=A\).
(3) A priori on devrait écrire ici une droite, car on ne sait pas que \(B\) ne peut pas être incidente à \(u\) et \(w\) simultanément. Ce sera montré au cours de la démonstration : résulte du fait que \(A, B, C\) ne sont pas alignés.
Ce théorème précise que s’il existe des milieux pour deux couples de points, le troisième couple admet aussi un milieu et les trois médianes sont en pinceau.
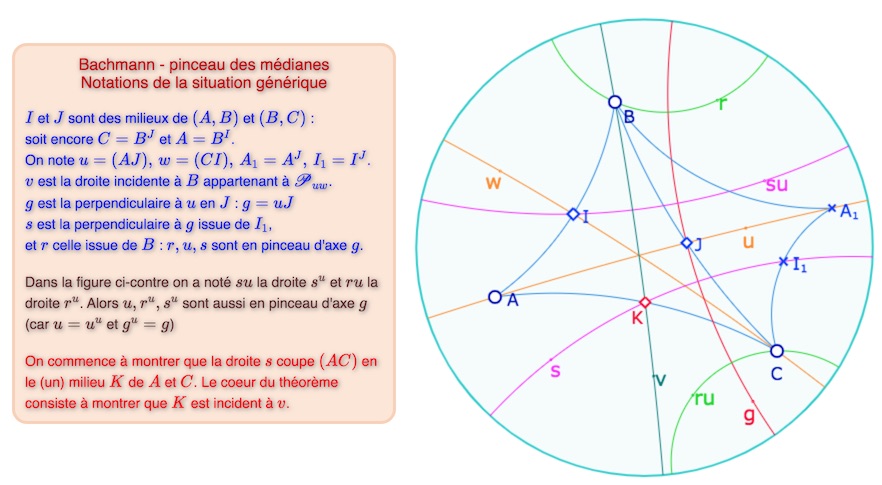
Lancer cette figure dans un nouvel onglet
Preuve du théorème : on construit les points \(A_1=A^J, I_1=I^J\) et \(g=uJ\) la perpendiculaire à \(u\) en \(J\). Soit \(s\) la perpendiculaire en \(g\) à \(I_1\). Cette droite \(s\) est définie (ie elle est bien unique) car \(I_1\) n’est pas le pôle de \(g\). En effet \(I^J=g\) donnerait \(I=g^J=g\). Mais alors on pourrait écrire \(C=B^J=B^{gu}=B^{Iu}=A^u=A\). Or c’est impossible car \(A, B, C\) sont distincts, puisque non alignés.
Alors on peut appliquer la réciproque du théorème des milieux (Th 23 de cette page) dans \(AA_1C\) : Tout d’abord \(I_1\) est milieu de \(C\) et \(A_1\). En effet, on a \(C^{I_1}=C^{JIJ}=JIJCJIJ=JI.JCJ.IJ=JIC^JIJ=JIBIJ=JB^IJ=JAJ=A_1\) . Par ailleurs \(g\), perpendiculaire à \((AA_1)\) en un milieu de \(A\) et \(A_1\) est une médiatrice, donc \(s\), perpendiculaire à \(g\) en \(I_1\) coupe \((AC)\) en un milieu de \(A\) et \(C\). D’où l’existence d’un point \(K\), de \(s\), milieu de \(A\) et \(C\) : \(K \mid s\), \(C^K=A\) et donc \(K \mid b=(AC)\).
Reste à montrer – l’essentiel du théorème – que \(K\) est incident à \(v\). Dans la suite, on note \(a=(BC), \; b=(CA)\) et \(c=(AB)\).
On considère maintenant \(r\) la perpendiculaire à \(g\) issue de \(B\). Là encore « la » car \(B\) n’est pas le pôle de \(g\). En effet \(B=g\) conduit à \(B=g=g^J=B^J=C\) ce qui n’est pas vrai.
Ainsi, les droites \(u, r\) et \(s\) sont en pinceau (à axe, elles sont orthogonales à \(g\)), alors les droites \(u, r^u, s^u\) sont aussi en pinceau (car \(u^u=u\)). Or \(r^u\) est la perpendiculaire à \(g\) issue de \(C\) et \(s^u\) celle issue de \(I\). Comme \(g\) est stable par \(u\), les droites \(u, r^u, s^u\) sont les antiappariées de \(u, r, s\) dans l’antiappariement du pinceau des droites orthogonales à \(g\).
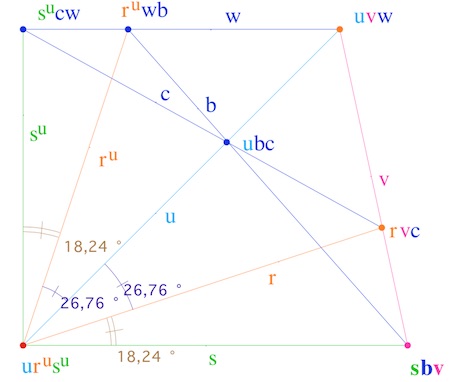
De plus \(v\) est en pinceau avec \(u\) et \(w\) d’une part (hypothèse sur \(v\)), et \(c\) et \(r\) d’autre part \(( \in \mathscr{P}_B)\). Si on peut appliquer le théorème de l’antiappariement, on aurait que \(s, b \), et \(v\) sont en pinceau.
On peut appliquer le théorème dans le cas particulier où \(c’\) et \(c^{\prime \prime}\) (du théorème général) sont confondues en la bissectrice des autres droites antiappariées du pinceau : ci-contre, dans l’illustration de l’application du théorème, il y a 5 droites au lieu de 6 issues du point symbolique \(a’b’c’=ur^us^u\).
Reste à vérifier la dernière hypothèse du théorème : \(wu \neq cr\). Or \(\mathscr{P}_{cr}\) est un pinceau centré sur \(B\), si les deux produits étaient égaux on aurait \(B \mid u,w\) ce qui aboutit à \(u=c\) et donc que \(A, B, J\) sont alignés. Il en résulterait que \(A, B, J\) et \(B^J\) seraient alignés, soit que \(A, B\) et \(C\) seraient alignés, ce qui n’est pas.
On a donc bien \(wu \neq cr\). Ainsi le théorème de l’antiappariement est applicable et le produit \(sbv\) est une droite. Mais cela ne suffit pas pour conclure. Car deux cas sont possibles :
Soit \(b \neq s\). Alors, de \(K \mid b,s\) il en résulte que le pinceau \(\mathscr{P}_{bs}\) est à centre \(K\) et donc que \(K\) est incident à \(v\) : la droite \(v\) est bien la médiane issue de \(B\), et les trois médianes sont en pinceau.
Soit \(b = s\), cela signifie que \(g\) est aussi orthogonale à \(b\) et donc qu’il existe de \(A\) deux perpendiculaires à \(g\), car \(b \neq u\) (sinon \(B=C\)). On sait que le seul cas où il n’y a pas unicité de la perpendiculaire en un point est que le point est le pôle de la droite : dans ce cas, on a alors \(A=g\).
D’une part, cela prouve que nous sommes en géométrie elliptique (revoir l’axiome de polarité de la page sur la séparation des géométries), et d’autre part que le théorème est montré dans toute géométrie où l’axiome de polarité n’est pas vérifié … ce qui en fait beaucoup.
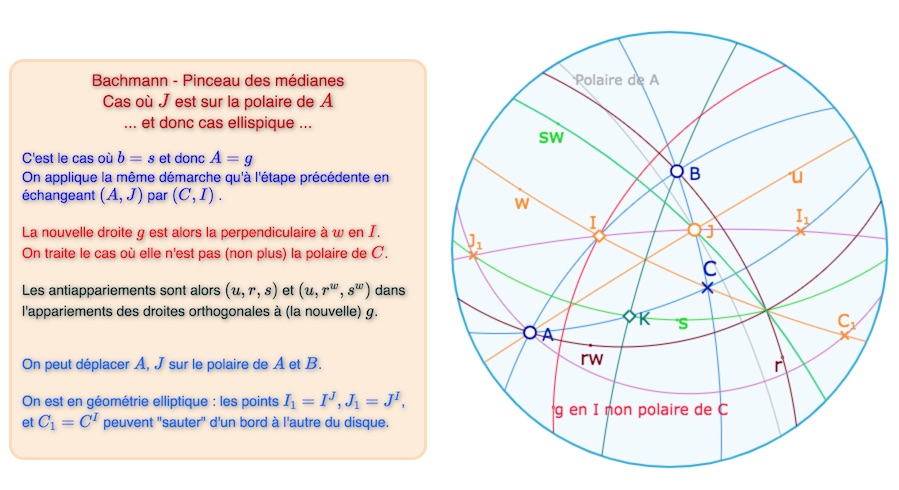
Premier cas particulier elliptique
Dans le cas où \(A=g\), illustration ci-dessus où \(J\) est à la fois sur la polaire de \(A\) et au milieu de \(B\) et \(C\), et on vérifie que \(I^J\) est bien sur \((BC)\). On peut appliquer la même démarche en \(I\) pourvu que la perpendiculaire (encore notée \(g\) ci-dessus) à \(w\) en \(I\) ne soit pas la polaire de \(C\). Alors la preuve se transpose sans problème en échangeant les rôles des points \((A, J)\) et de ceux de \((C, I)\).
Lancer la figure associée à cette illustration dans un nouvel onglet.
Reste à traiter le cas où l’on a simultanément \(A=g=uJ\) et \(C=wI=h\). Si on manipule la figure précédente pour se placer dans ce cas, on ne réalise en fait qu’un cas particulier où les droites \(a\) et \(c\) sont confondues avec les polaires de \(C\) et \(A\). Par contre on observe déjà que \(I_1\) et \(J_1\) coïncident.
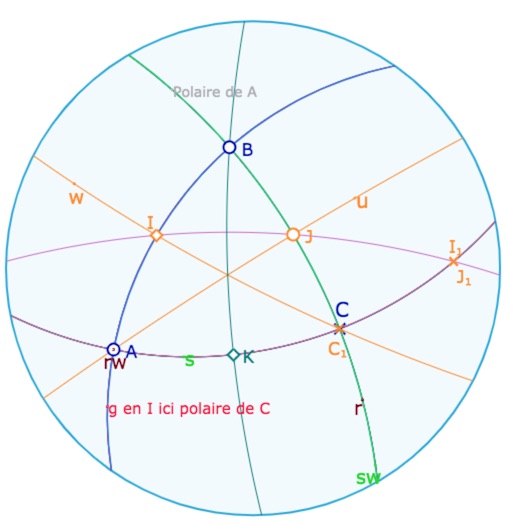
Le second cas particulier réalisé avec la figure précédente
Mais on peut réaliser une figure plus fine où \(I\) et \(J\) sont sur les polaires de \(C\) et \(A\) sans que les côtés du triangles soient eux mêmes ces polaires, dont voici une illustration.
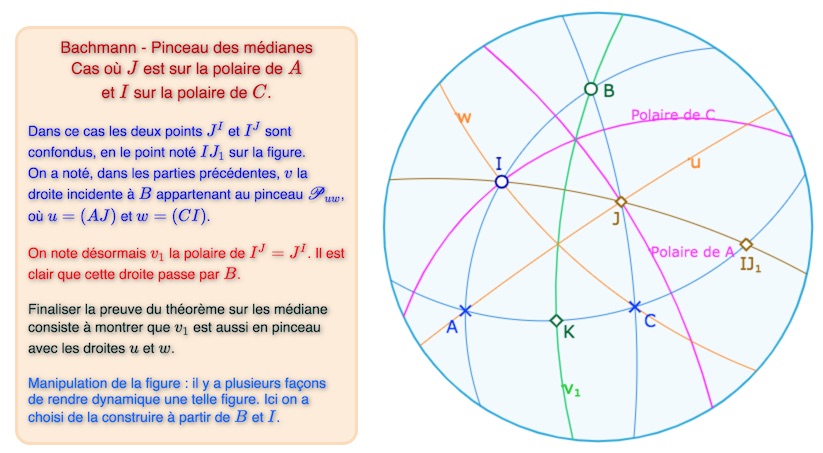
Le second cas particulier, dans son cas le plus générique. On agit sur \(B\) et \(I\) uniquement.
Bien entendu la figure ne se fait pas trivialement : \(B\) et \(I\) donnés, on construit \(A\). \(J\) doit être construit sur la polaire de \(J\) tout en ayant \(C=B^J\) sur la polaire de \(I\).
Ouvrir cette figure dans un nouvel onglet.
On se place donc dans ce cas \(A=g=uJ\) et \(C=wI=h\) (illustration ci-dessus). Alors non seulement \(I^J\) mais aussi \(J^I\) sont sur la droite \(b=(AC)\). De plus ces deux points sont à la fois sur \(b\) et sur \((IJ)\). Ces deux droites étant distinctes (sinon \(A, B, C\) seraient alignés), leur intersection est réduite à un point et donc \(I^J=J^I\), noté \(IJ_1\) dans la figure ci-dessus. En remarquant que \(B \neq J^I\) car sinon \(B\) serait aligné à \(A\) et \(C\), et de même \(B \neq I^J\) on peut alors écrire :
\(B^I=A=g \) donc \(B^I \mid J\) soit \(B \mid J^I\). De même\(B^J= C= h \) donc \(B^J \mid I\) soit \(B \mid I^J\)
Soit alors \(v_1\) la polaire de \(I^J = J^I\) (et donc \(v_1 = I^J = J^I\)). Alors \(v_1\) est orthogonale à \((IJ)\) et \(b\). De \(B \mid J^I\) ci-dessus, il vient \(B \mid v_1\), la droite \(v_1\) passe par \(B\).
On peut écrire \(J^{v_1}= v_1Jv_1 = (JIJ).J.(IJI)=I\) soit \(J^{v_1}=I\). De même, il vient \(B^{Jv_1}=B^{IJ}=JIBIJ\). Mais \(B^I \mid J\) s’écrit aussi \(IBIJ=JIBI\) et donc \(B^{Jv_1}=IBI=B^I\) soit \(C^{v_1}=A\).
En définitive \((AJ)^{v_1}=(A^{v_1}J^{v_1})=(CI)\) et donc \(u^{v_1}=w\). Il en résulte que les droites \(u, v_1\) et \(w\) sont en pinceau car de \(v_1u=wv_1\) il vient \(uwv_1=uv_1u=v_1^u\) est une droite.
Comme \(v\) et \(v_1\) sont en pinceau avec \(u\) et \(w\) et chacune étant incidente à \(B\), par unicité de la droite d’un pinceau incidente à un point n’appartenant aux deux droites, il en résulte que \(v\) et \(v_1\) sont confondues. Ainsi, dans ce cas particulier, \(v\) est aussi en pinceau avec \(u\) et \(w\).
Ainsi les médianes de trois points, comme définies dans le théorème, sont toujours en pinceau. D’une manière absolue nous ne pouvons pas aller plus loin (préciser le type de pinceau) car nous avons vu un exemple (qui plus est euclidien) où les médianes sont en pinceau à axe.
En fait, il est clair que les médianes sont concourantes dans le cas elliptique puisqu’il n’existe qu’un seul type de pinceau . Il faudrait alors montrer que les médianes sont concourantes dans le cas euclidien (sauf si la caractéristique du corps associé est égale à 3) et surtout – c’est le plus délicat – dans le cas hyperbolique. Les démonstrations sont plus simples quand on se place dans une géométrie donnée, avec ses axiomes et ses outils propres.
Bachmann lui-même ne montre le concours des médianes uniquement qu’en appendice de son ouvrage, en particulier après le plongement des plans métriques dans un plan idéal projectif, et en utilisant ce plan idéal : l’avantage est que le résultat est alors montré pour des géométries un peu plus générales (semi-euclidiennes, semi-hyperboliques) qu’en séparant les géométries elles-mêmes. Mais le prix a payer est assez conséquent.
Les théorèmes de Brianchon et Pappus
L’un des objectifs de Bachmann est de plonger toutes les géométries produites par son axiomatique dans un plan projectif métrique idéal, et retrouver ainsi, en les généralisant, les résultats de Dehn dans le cadre des géométries métriques (au sens de munis d’une distance de Cayley). On se propose ici, comme application de l’antiappariement, de voir deux des premiers théorèmes fondamentaux qui donneront à ce plongement les structures algébriques attendues.
Il s’agit d’explorer deux théorèmes essentiels pour l’algébrisation dans le vocabulaire des pinceaux. On doit à Hessenberg la démonstration suivante (1930) du théorème absolu de Brianchon (et de Pappus) sur la base de son théorème de l’antiappariement, preuve qu’il place en parallèle de celle, affine, de Hilbert pour le théorème de Pappus (que Hilbert appelle de Pappus-Pascal).
Le théorème de Brianchon sur les pinceaux
Soient deux pinceaux à centre \(A\) et \(B\) composés de six droites \(a_{i \, (1 \le i \le 3)}\) et \(b_{j \, (1 \le j \le 3)}\) incidentes respectivement à \(A\) et \(B\), aucune n’étant incidente aux deux points. Les pinceaux \(\mathscr{P_{\mathit{a_i \, b_j}}}\) (\(i \neq j\)) sont appelés les sommets de l’hexagramme. Par unicité de l’intersection de deux pinceaux, les six sommets sont distincts et distincts des pinceaux à centre \(\mathscr{P_\mathit{A}}\) et \(\mathscr{P_\mathit{B}}\) . Les pinceaux \(\mathscr{P_\mathit{{a_i b_j}}}\) et \(\mathscr{P_\mathit{{a_j b_i}}}\) sont dits opposés.
On suppose désormais que les trois paires de faisceaux opposés ont chacun une intersection non vide et donc qu’il existe trois droites appelées diagonales de l’hexagramme. On notera \(c_k\) la diagonale joignant les sommets \(\mathscr{P_{\mathit{a_i b_j}}}\) et \(\mathscr{P_{\mathit{a_j b_i}}}\) pour les permutations circulaires \((i, j, k)\) dans \(\{1, 2, 3\}\).
Théorème de Brianchon : Sous ces hypothèses, si deux diagonales ont un point commun \(C\), alors les trois diagonales sont concourantes en \(C\).
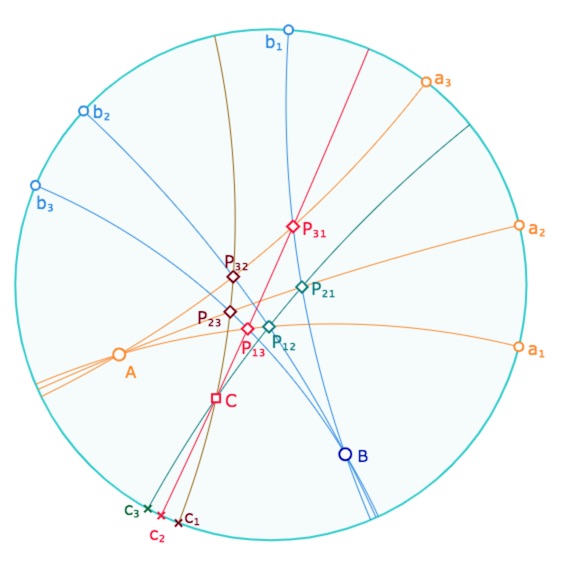
Illustration du théorème de Brianchon absolu (de pinceaux)
Preuve du théorème : tout d’abord on peut supposer les trois diagonales distinctes car si deux sont confondues le résultat est trivial. À une numérotation près, on peut supposer que \(C\) est l’ intersection des diagonales \(c_2\) et \(c_3\). Toujours par unicité de l’ intersection de deux pinceaux, \(\mathscr{P_\mathit{C}}\) est différent à la fois des six autres sommets \(\mathscr{P_{\mathit{a_i \, b_j}}}\) mais aussi de \(\mathscr{P_\mathit{A}}\) et \(\mathscr{P_\mathit{B}}\). En particulier \(C\) est un point différent de \(A\) et \(B\). Il en résulte aussi que pour chaque pinceau \(\mathscr{P_{\mathit{a_i b_j}}}\), il existe une unique droite \(c_{ij}\) incidente à \(C\) et appartenant à \(\mathscr{P_{\mathit{a_i b_j}}}\). Comme \(c_2\) est incidente à \(C\), \(c_{13}=c_{31}=c_2\). De même, \(c_3\) étant incidente à \(C\), on a aussi \(c_{12}=c_{21}=c_3\). Dans ce contexte, le théorème sera montré si on montre que \(c_{23}=c_{32}\). Car alors cette droite commune sera \(c_1\) et donc \(c_1\) sera incidente à \(C\).
Notons désormais \(a=(AC)\) et \(b=(BC)\). Alors dans \(\mathscr{P_\mathit{C}}\) les droites \(a\) et \(b\) déterminent un antiappariement(4). On note \(d_{uv}\) l’antiappariée de \(c_{uv}\) dans \(\mathscr{P_{\mathit{ab}}}\) : \(ac_{uv}=d_{uv}b\).
(4) Éventuellement une réflexion si \(a=b\), bissectrice des droites comme dans le théorème précédent sur les médianes.
Remarquons tout de suite que \(c_{12}=c_{21}\) implique qu’il en est de même des antiappariées : \(d_{12}=d_{21}\). Et pour les mêmes raisons on a aussi \(d_{13}=d_{31}\), on peut donc utiliser indifféremment \(d_{kj}\) ou \(d_{jk}\) dans les figures suivantes : ce sont les mêmes droites.
Nous allons appliquer trois fois le théorème de l’antiappariement à trois trilatères \((b_i, a_j, a_k)\) pour les trois permutations circulaires de \((i , j, k)\) dans \(\{1, 2, 3\}\). Dans un premier temps voyons que les deux pinceaux \(\mathscr{P_\mathit{B}}\) et \(\mathscr{P_{\mathit{a_j d_{ki}}}}\) sont distincts. Tout d’abord \(a_j \neq d_{ki}\) car \(d_{ki}\) est incidente à \(C\) alors que \(a_j\) ne l’est pas, on a donc bien d’un pinceau. Ensuite \(a_j \in \mathscr{P_{\mathit{a_j d_{ki}}}}\) alors que \(a_j \notin \mathscr{P_\mathit{B}}\) ainsi les deux pinceaux sont bien distincts.
On peut alors noter \(g_i\) la droite commune aux deux pinceaux. Elle existe toujours car un des deux pinceaux est à centre. Pour appliquer le théorème de l’antiappariement à la droite \(g_i\), il reste à vérifier la dernière hypothèse du théorème, à savoir que les produits \(b_ib\) et\(a_j d_{ki}\) sont différents, ce qui est vrai car \(B\) est incident à \(b_i\) et \(b\) mais pas à \(a_j\). On en déduit donc que \(g_i\), appartenant aux pinceaux \(\mathscr{P_\mathit{B}}\) et \(\mathscr{P_{\mathit{a_j d_{ki}}}}\) par définition, appartient aussi au pinceau \(\mathscr{P_{\mathit{a_k d_{ji}}}}\)
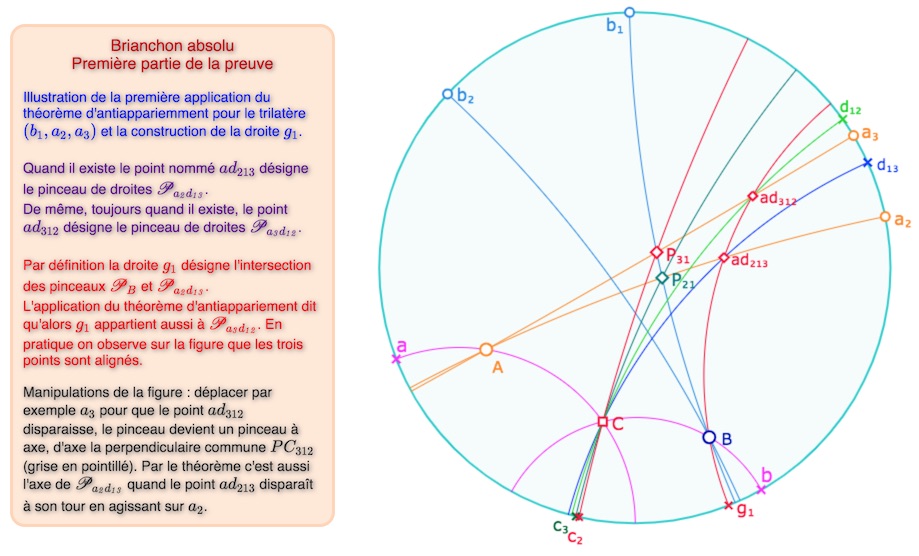
Première application du théorème d’antiappariement, ci dessus avec des pinceaux à centre, ci-dessous avec un ou deux pinceau à axe,
en déplaçant les points comme indiqué dans l’illustration.
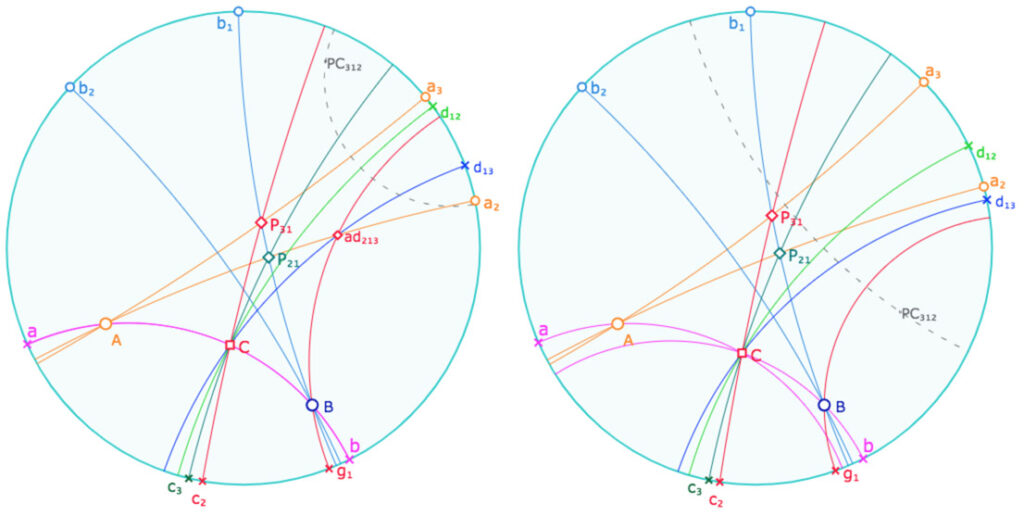
Lancer cette figure dans un nouvel onglet
En détaillant les trois applications du théorème d’antiappariement, on peut écrire :
• \(g_1\) appartient aux pinceaux \(\mathscr{P_\mathit{B}}\), \(\mathscr{P_{\mathit{a_2 d_{31}}}}\) et \(\mathscr{P_{\mathit{a_3 d_{21}}}}\)
• \(g_2\) appartient aux pinceaux \(\mathscr{P_\mathit{B}}\), \(\mathscr{P_{\mathit{a_1 d_{32}}}}\) et \(\mathscr{P_{\mathit{a_3 d_{12}}}}\)
• \(g_3\) appartient aux pinceaux \(\mathscr{P_\mathit{B}}\), \(\mathscr{P_{\mathit{a_2 d_{13}}}}\) et \(\mathscr{P_{\mathit{a_1 d_{23}}}}\).
Mais des égalités \(d_{13}=d_{31}\) et \(d_{12}=d_{21}\), on en déduit que \(g_1=g_2\) puis que \(g_1=g_3\) et donc que \(g_1\) appartient aux deux pinceaux \(\mathscr{P_{\mathit{a_1 d_{23}}}}\) et \(\mathscr{P_{\mathit{a_1 d_{32}}}}\). Ce qui permet d’écrire que les droites \(d_{23}\) et \(d_{32}\) appartiennent au pinceau \(\mathscr{P_{\mathit{a_1 g_1}}}\), et bien entendu à \(\mathscr{P_\mathit{C}}\) par définition des droites \(d_{uv}\). Là encore \(\mathscr{P_{\mathit{a_1 g_1}}}\) est bien un pinceau (\(a_1 \neq g_1\) car \(B\) est incident à \(g_1\) et pas à \(a_1\)) et les deux pinceaux sont distincts car \(a_1 \in \mathscr{P_{\mathit{a_1 g_1}}}\) et \(a_1 \notin \mathscr{P_\mathit{C}}\). Les deux droites, intersections des deux pinceaux, sont donc égales : \(d_{23}=d_{32}\), et il en est de même de leurs antiappariées \(c_{23}=c_{32}\).
On a donc \(c_1 = c_{23} =c_{32}\), et en particulier \(C \in c_1\) : le théorème de Brianchon est démontré.
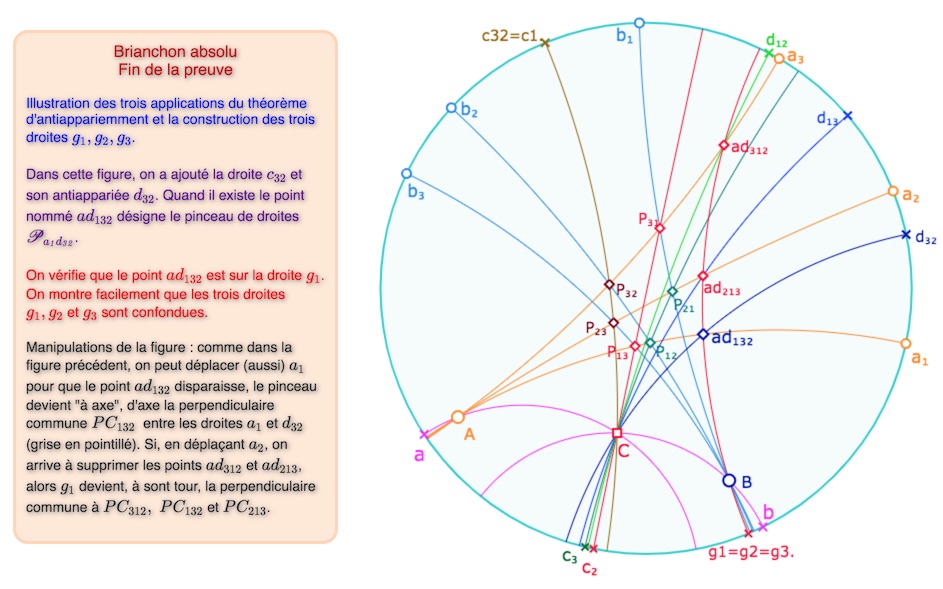
Version finale de la preuve. Ci dessus avec les trois pinceaux à centre : les points \(ad_{312}, ad_{213}\) et \(ad_{132},\) existent.
Ci-dessous avec un, deux ou même trois pinceaux à axe. Les droites \(g_i\) comme perpendiculaire commune aux axes de trois pinceaux.
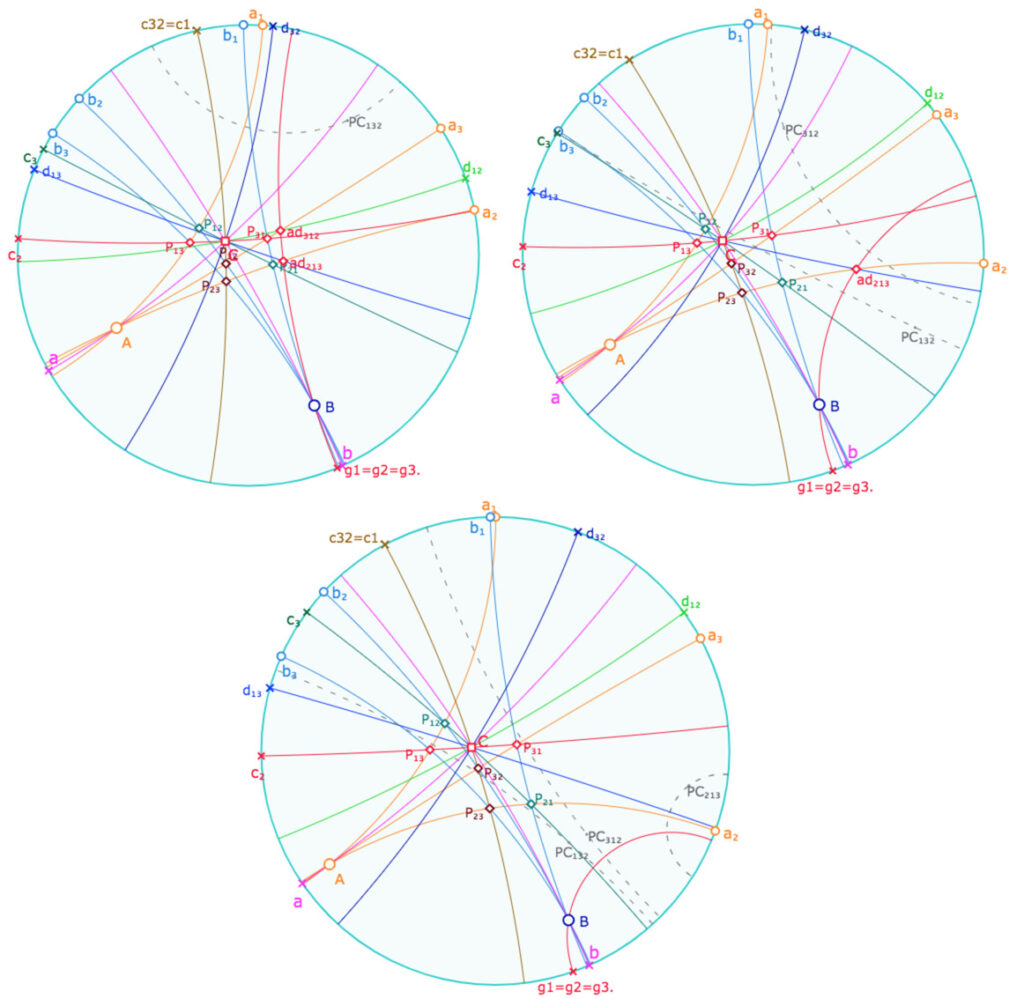
Lancer cette nouvelle figure dans un nouvel onglet.
Les représentations de Bachmann lui-même
Extension dans le cas où le point \(C\) n’existe pas
En fait, il n’est pas nécessaire que \(C\) existe pour aboutir au théorème Brianchon. On a une extension naturelle, qui utilise, en fait, les mêmes arguments, pourvu que les trois diagonales \(c_1, c_2, c_3\) existent. En voici un résumé en quelques illustrations.
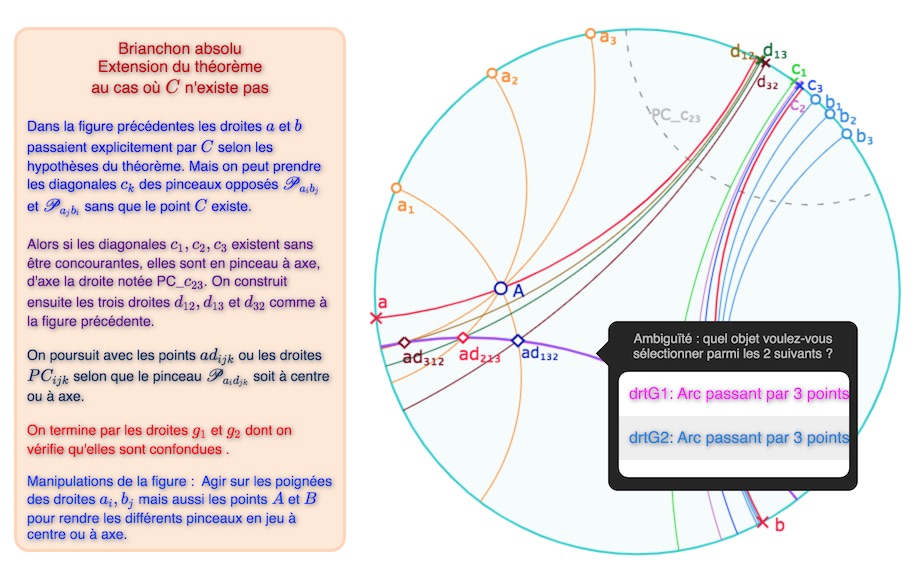
D
Dans l’illustration ci-dessus, \(C\) n’existe pas, les trois pinceaux de la forme \(\mathscr{P_{\mathit{a_j d_{ki}}}}\) sont à centre, de centre \(ad_{jki}\). On a construit \(g_1\) et \(g_2\) nommées \(drtG_1\) et \(drtG_2\).
Ci-dessous, cas ou deux ou trois des pinceaux \(\mathscr{P_{\mathit{a_j d_{ki}}}}\) sont à axe, d’axe \(PC_{jki}\).
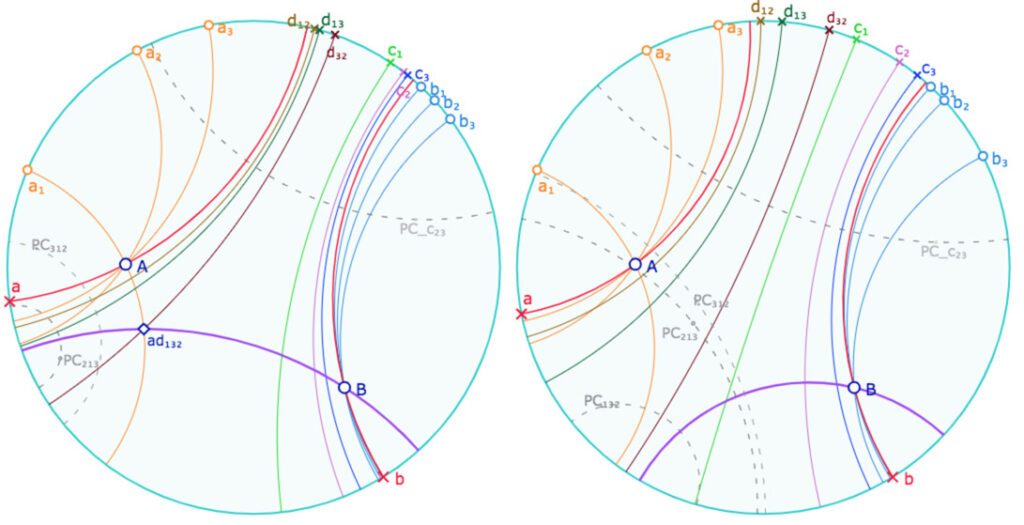
Lancer cette figure dans un nouvel onglet.
Bien entendu, il existe des situations où les trois diagonales n’existent pas simultanément.
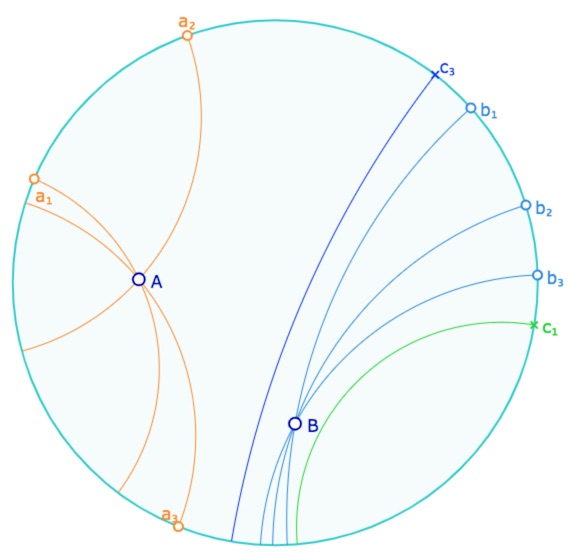
Exemple de configuration où une diagonale n’existe pas : ici \(c_2\) n’existe pas.
Théorème de Pappus
La principale conséquence de ce théorème est la lecture «projective» qu’en fait Bachmann : en inversant les rôles de droites et de points, il lit dans le théorème précédent, celui de Pappus.
Théorème de Pappus : Si les sommets \(A_{i \, (1 \le i \le 3)}\) et \(B_{j \, (1 \le j \le 3)}\) d’un hexagramme sont respectivement sur deux droites données \(a\) et \(b\), les trois intersections \(C_i\) des diagonales opposées \((A_jB_k)\) et \((A_kB_j)\) – pour \(i, j , k\) différents – sont alignés.
Les théorèmes de Pappus et Brianchon sont duaux l’un de l’autre en échangeant les notions de « points » et « droites » ainsi que les expressions « passer par deux points » et « intersection de deux droites ». Voici la relecture de la figure de Brianchon que propose Bachmann pour y voir le théorème de Pappus.

Dans cette figure, les diagonales ne sont pas construites par les points \(A_i\) et \(B_j\) mais comme intersections de deux pinceaux. Ainsi elles existent (ou peuvent exister) même si les pinceaux associés ne sont plus à centre. Voici deux illustrations, une où tous les points \(A_i\) et aucun \(B_j\) existent et l’autre où c’est l’inverse, et dans les deux cas les trois points \(C_k\) existent.
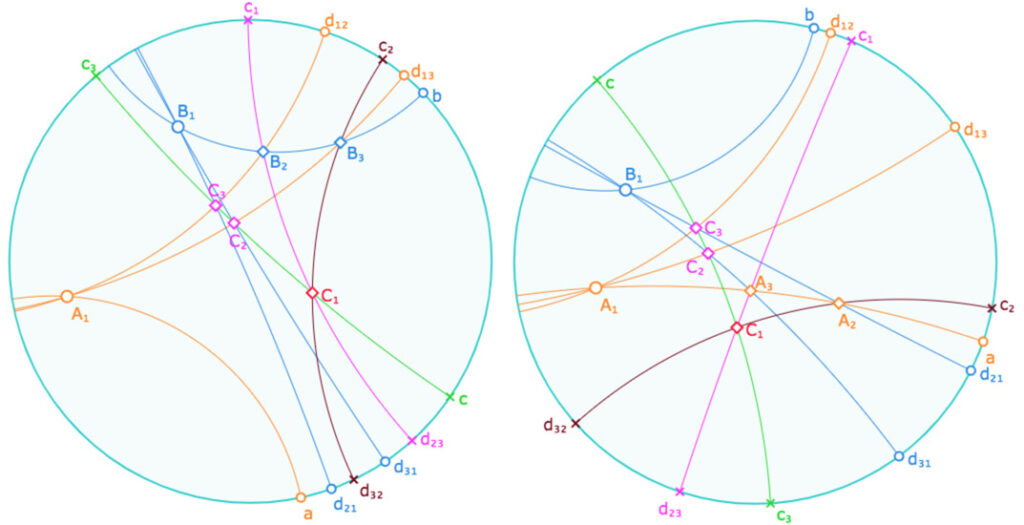
Voici deux autres illustrations, une avec un sommet \(B_j\) et un sommet \(A_k\), l’autre avec aucun point de Pappus, autres que les centres des pinceaux \(A_1\) et \(B_1\) existent, alors que les trois points \(C_k\) existent.
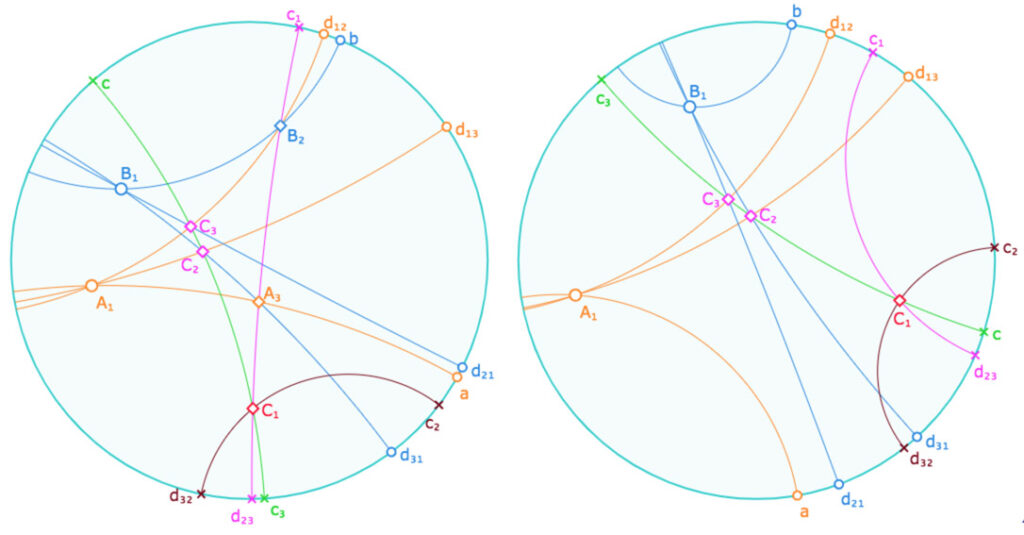
Le théorème de Pappus dans ses extensions possibles
Ouvrir la figure associée dans un nouvel onglet.
La démarche de l’axiomatique de Bachmann, prend ici une dimension mathématique plus classique, celle de la généralisation des propriétés essentielles à des objets plus abstraits : le théorème de Pappus, vrai sur ces nouveaux objets que sont les pinceaux, permet de les considérer comme objets élémentaires (points idéaux) d’une nouvelle structure pour laquelle, en y plongeant toute l’axiomatique déployée jusque-là, dont Bachmann va montrer qu’elle a bien les propriétés structurelles attendues : celle d’être un plan projectif « métrique », c’est-à-dire un plan projectif d’incidence muni d’une orthogonalité et d’isométries qui prolongent celles du plan métrique. C’est l’objet des trois prochaines pages de ce menu.