«Les périples du voyage me firent oublier mes travaux mathématiques; arrivés à Coutances, nous montâmes dans un omnibus pour je ne sais quelle promenade ; au moment où je mettais le pied sur le marchepied, l’idée me vint, sans que rien dans mes pensées antérieures parût m’y avoir préparé, que les transformations dont j’avais fait usage pour définir les fonctions fuschiennes étaient identiques à celles de la géométrie non euclidienne. »
Henri Poincaré – L’invention mathématique – 1908 (Ed. Jacques Gabay 2011 p 141)
» … je veux parler de la Géométrie non euclidienne. Cette Géométrie, fondée sur l’hypothèse que la somme des angles d’un triangle est plus petite que deux droits, ne semble d’abord qu’un simple jeu de l’esprit qui n’a d’intérêt que pour le philosophe, sans pouvoir être d’aucune utilié au mathématicien. Il n’en est rien ; les théorèmes de la géométrie de Lobatchevsky sont aussi vrais que ceux de la géométrie d’Euclide, à la condition qu’on les interprète comme ils doivent l’être. Ainsi, par exemple, ces théorèmes ne sont pas vrais de la ligne droite, telle que nous la concevons, mais ils le deviennent si, partout où Lobatchevsky dit une droite, nous disons un cercle qui coupe orthogonalement le cercle fondamental. Je me trouvais donc en présence de toute une théorie, imaginée, il est vrai, dans un but métaphysique, mais dont chaque proposition, convenablement interprétée, me fournissait un théorème applicable à la Géométrie ordinaire. Il se trouva qu’en combinant tous ces théorèmes, j’obtins aisément la solution de la difficulté dont j’ai parlé plus haut. »
Henri Poincaré – « Analyse des travaux scientifiques de Henri Poincaré faite par lui- même »
(écrit à la demande du mathématicien Mittag-Leffler en 1901) publié dans Acta 38 en 1921
Poincaré construit alors deux modèle conformes de la géométrie hyperbolique : le « disque de Poincaré » dont il est question ci-dessus avec lequel nous allons développer les pages suivantes, et le « demi-plan de Poincaré »
La « géométrie de Lobatchevsky » ne s’appelait pas encore « hyperbolique » en 1901. C’est une géométrie pour laquelle par un point il ne passe pas une, mais deux parallèles à une droite donnée, selon la définition de Lobatchevsky de 1826 (et non pas une infinité comme on peut le lire parfois).
Le menu DP (Disque de Poincaré)
Dans ce menu, on commence par un item d’exploration sur les droites, à la découverte « expérimentale », dans le modèle du disque de Poincaré, un peu comme les enfants explorent la géométrie euclidienne avec les outils qu’on leur donnent :
• un règle pour tracer les segments et les droites,
• une équerre pour tracer des perpendiculaires
• un compas pour tracer les cercles
Un item est ensuite consacré au cycles hyperbolique, extension du concept de cercle.
Le troisième item invite à jouer avec les pavages hyperboliques, activités proposées comme réflexion sur les polygones réguliers. On choisit ici une approche, là encore résolument exploratoire, sans entrer dans le détail des constructions effectives des cercles de pavage pour lesquels on a consacré d’autres développements plus techniques.
Les deux derniers items de ce menu sur le disque de Poincaré est l’occasion d’aller un peu plus loin dans une extension conceptuelle générale, particulièrement parlante en géométrie dynamique : il s’agit de passer des triangles aux trilatères pour voir, dans le cadre hyperbolique, une extension surprenante – pour qui les découvre bien entendu – de nombreux théorèmes usuels de la géométrie du triangle. On commence par un item sur les premières propriétés des pinceaux de droites. Un item spécifique est consacré aux bissectrices et à la question de la continuité des réalisations implémentées et la construction de Malfatti de trilatère.
Le modèle du disque de Poincaré
Un modèle est donc une représentation, dans notre plan usuel, de la géométrie que l’on veut étudier pour lequel on sait faire des correspondances entre les objets de la géométrie et ceux du modèle.
Ainsi dans le modèle du disque de Poincaré :
- Les points hyperboliques sont à l’intérieur d’un cercle que l’on appelle horizon. Le cercle fondamental de Poincaré est le cercle unité. Les calculs y sont simplifiés.
- Les points du cercle horizon sont les points à l’infini sur les droites hyperboliques. Ce ne sont pas des points du plan hyperboliques. On parlera de points idéaux.
- Les droites hyperboliques sont des arcs de cercle qui coupent l’horizon de manière perpendiculaire (les tangentes sont perpendiculaires), avec le cas particulier de la droite qui passe par le centre de l’horizon : c’est alors le diamètre associé du cercle.
- La symétrie axiale est simplement l’inversion par rapport à la droite (c’est en fait l’origine du modèle).
- Propriété 1 : les cercles hyperboliques sont des cercles euclidiens mais leur centre n’est pas le même bien entendu.
- Propriété 2 : le modèle est conforme : les droites se coupent, hyperboliquement, selon l’angle dont on les voit se couper dans le modèle.
A l’époque de Poincaré, en particulier pour ses contemporains géomètres, la question du plongement d’une géométrie – fût-elle « nouvelle » ou « hyperbolique » dans une géométrie projective plus globale, est un point important. Dans ce contexte, le cercle horizon correspondant à la « droite de l’infini ».
D’un point de vue technique, de réalisation des figures ou des macro-constructions, avoir accès aux points à l’infini des droites hyperbolique peut parfois simplifier les constructions.
Illustration introductive avec les hauteurs d’un triangle
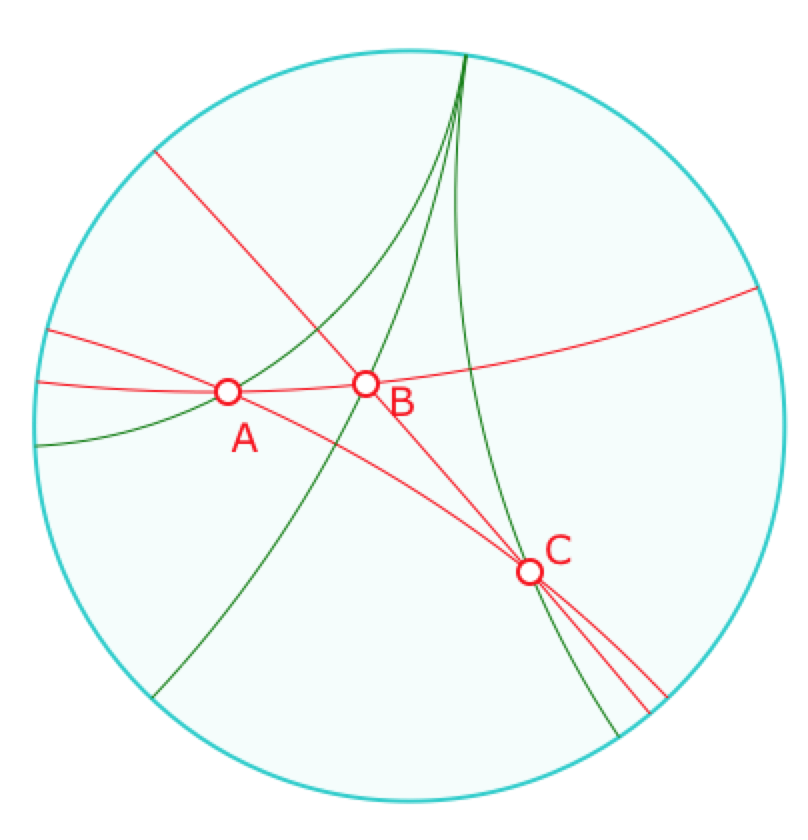
Ci-dessous, en rouge le triangle \(ABC\) avec les trois droites \((AB), (AC), (BC)\)), (BC). En vert les hauteurs du triangle.
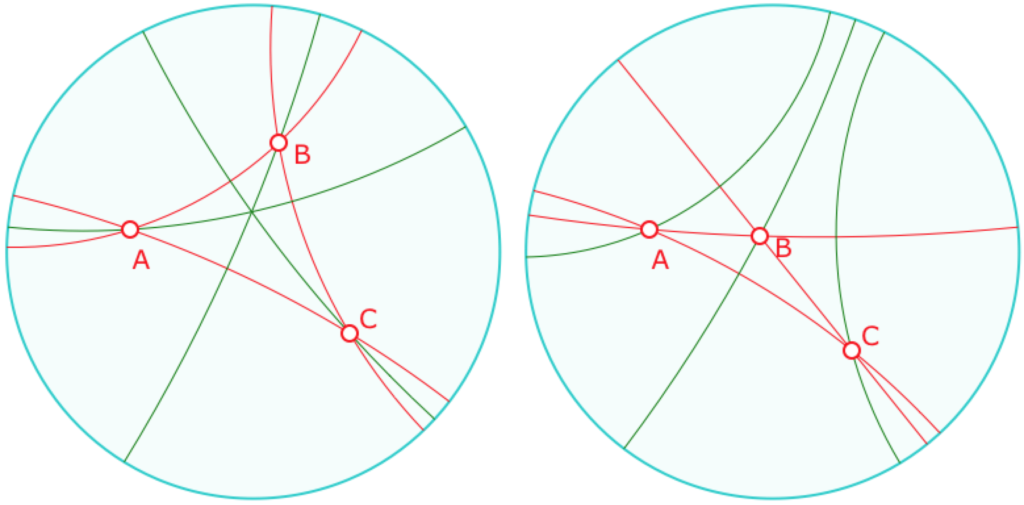
à gauche, les hauteurs sont concourantes, à droite, elles sont non sécantes.
Dans l’illustration suivante, les trois hauteurs semblent se «couper à l’infini» c’est-à-dire sur le cercle horizon.
Nous allons peu à peu découvrir les propriétés des droites particulières du triangle, et voir que ces trois configurations peuvent se décrire par un invariant commun.