Avec cette problématique d’envoyer la pseudosphère dans le disque limite de Beltrami, nous allons être plus concrètement concernés par la représentation des différentes feuilles de la pseudosphère dans le disque, et plus précisément par la place de la feuille principale. On a naturellement choisi de paramétrer cette feuille principale par une longitude allant de \(0\) à \(2\pi\). Or nous allons voir que ce n’est pas le plus pertinent. Nous serons donc être amené à modifier les calculs naturels pour retrouver une certaine symétrie dans les configurations.
Dans un premier temps, il s’agit d’adapter les calculs de Beltrami, qui utilisait ses « coordonnées curvilignes » – que l’on présentera dans l’item d’illustrations de son Essai d’interprétation – à notre système (latitude, longitude) qui s’apparente plutôt à des coordonnées « pseudo-cylindriques ». On trouve alors, pour un équateur de rayon 1 et un cercle limite aussi de rayon 1, la paramétrisation \((u, \theta) \rightarrow (x,y)\) suivante :
\(x=\displaystyle \frac{\theta^2+ch^2(u)-1}{\theta^2+ch^2(u)+1}\) et \(y=\displaystyle \frac{-2\theta}{\theta^2+ch^2(u)+1}\)
Remarques
• le signe « – » en \(y\) n’est pas produit par le calcul, il a été ajouté pour qu’un mouvement dans le sens trigonométrique sur un cercle parallèle à l’équateur (un horicycle pour la pseudosphère) correspond à un mouvement de même sens sur l’horicycle image dans le disque limite de Beltrami.
• les rayons égaux à 1 dans les calculs n’est pas une contrainte dans les représentation en géométrie dynamique puisque l’implémentation logicielle de la géométrie est affine et barycentrique : si on augmente le rayon du cercle, tout est modifié homothétiquement, c’est juste le rapport à l’unité qui change.
La paramétrisation de Beltrami associe l’origine de son repère curviligne (\(u=0, v=0\), nous y reviendrons en détail au prochain item) qui correspond pour nous à \(\theta=0, u=0\), à l’origine du cercle-limite (\(O_{dl}\) ci-dessous). Il est immédiat aussi que, dans cette correspondance \(0 \le x <1\), et donc que l’image de la pseudosphère est incluse dans un demi-disque. La représentation étant symétrique à l’axe des abscisses, on peut s’intéresser à \(y \ge 0\). L’ordonnée est maximale pour \(ch(u)\) minimal, c’est-à-dire égal à 1, soit \(u=0\) et donc quand les points de la pseudosphère sont sur le cercle équateur. Dans ce cas, les projections \(x\) et \(y\) vérifient alors : \(\displaystyle \frac{\left( x-\displaystyle \frac{1}{2}\right)^2}{\displaystyle \left( \frac{1}{2}\right)^2}+\displaystyle \frac{y^2}{\left( \frac{1}{\sqrt{2}}\right)^2}=1\).
L’image de la pseudosphère est donc à l’intérieur d’une ellipse, qui plus est tangente au disque limite, donc à l’intérieur d’un horicycle du modèle de Klein Beltrami. Une première conséquence est que la pseudosphère, comme modélisation du plan de Lobatchevsky, n’a qu’un point à l’infini accessible : le centre de cet horicycle pour le modèle KB, soit le point \(I_{dl} (1,0)\). On voit aussi que ce point idéal peut être atteint de deux façons :
• pour \(\theta\) donné (on est sur un méridien) quand \(u\) tend vers l’infini : c’est le point à l’infini physique de la pseudosphère comme surface plongée dans l’espace euclidien.
• pour \(u\) donné – on est alors sur un parallèle (à l’équateur) – quand \(\theta\) tend vers l’infini : ce point à l’infini du plan hyperbolique s’atteint aussi par un enroulement infini sur un parallèle de la pseudosphère, à altitude constante, dans un sens ou dans l’autre.
Ce contact unique de la pseudosphère avec l’infini justifie que, depuis la terminologie de Klein, la pseudosphère est dite aussi, en terme de modèle du plan de Lobatchevsky, un modèle parabolique.
Réglage de l’image de la feuille principale
par choix de paramétrisation de la longitude
La feuille principale (\(0 \le \theta < 2\pi\)) est limitée par les deux segments d’origine \(I_{dl}\) et d’extrémité \(O_{dl}\) pour le premier et le point – \(F_{+}\) ci-dessous – de coordonnées \(\displaystyle \left( \frac{4\pi^2}{4\pi^2+2}, \displaystyle \frac{-4\pi}{4\pi^2+2} \right)\) pour le second. Dans cette paramétrisation, la feuille principale est donc projetée dans la moitié inférieure de l’horicycle image de la pseudosphère, la partie supérieure correspondant à la feuille précédente.
Par contre, si on paramètre la feuille principale sur l’intervalle \(-\pi \le \theta < pi\) alors la feuille principale est limitée par les segments allant de \(I_{dl}\) vers les points – \(F_{+\pi}\) et \(F_{-\pi}\) ci-dessous – de coordonnées \(\displaystyle \left( \frac{\pi^2}{\pi^2+2}, \displaystyle \pm \frac{2\pi}{\pi^2+2} \right)\), ce qui d’une par produit un domaine symétrique par rapport à l’axe des abscisses, et d’autre part augmente la couverture de la feuille principale dans l’horicycle. D’une manière générale, la paramétrisation de Beltrami favorise fortement la représentation de la feuille principale.
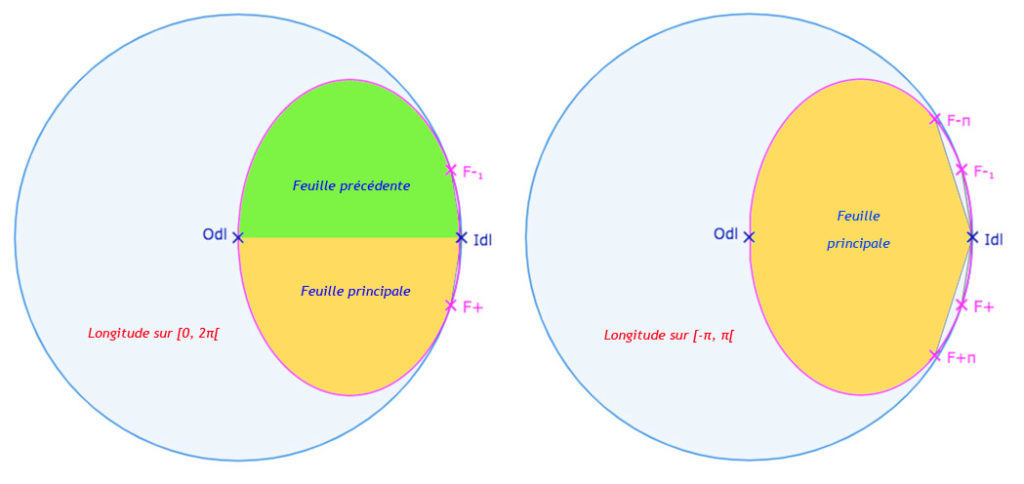
à gauche la paramétrisation utilisée dans les pages précédentes qui donne une part égale à la feuille principale et la feuille précédente.
à droite une paramétrisation décalée de \(\pi\) étend la représentation de la feuille principale sur une partie presque deux fois plus grandes et surtout symétrique.
Ce sera celle retenue dans les prochaines figures de conjugaison, pour. une meilleure lisibilité de la feuille principale.
Le retour de KB sur PS
Il est donné par les relations \(\displaystyle \theta=\frac{y}{x-1}\) et \(u=ch^{-1}\displaystyle \left(\frac{\sqrt{1-x^2-y^2}}{1-x}\right)\) (car \(x<1\)).
Longitude qu’il faut adapter, à \(\pi\) près selon la paramétrisation retenue pour la feuille principale, d’où des macros booléennes, vers KB et vers PS, mises en oeuvre dans la figure suivante.
Figure d’illustration (et d’appropriation) de la conjugaison
La figure que l’on propose sur ce thème est riche d’illustrations de nombreuses situations. Les trois droites de la pseudosphère sont construites par les macros intrinsèques des pages précédentes. Les points \(A, B, C\) sont ensuite envoyés sur le disque limite de Beltrami, en \(A_{kb}, B_{kb}, C_{kb}\), avec \(kb\) pour Klein Beltrami, mais aussi Booléen. Les droites sont construites dans KB. On voit déjà clairement que les droites sortent de l’horicyce rose, image de la pseudosphère, et donc que des points peuvent être sur ces droites sans pouvoir être sur la pseudosphère … à ne pas oublier pour la suite. Voici quelques manipulations à effectuer
• Tout d’abord, sans modifier les pop-up menus commencer par déplacer les points \(A, B, C\) par leurs longitudes. Remarquer que l’enroulement des droites plusieurs fois sur la pseudosphère correspond à la proximité de la KB-droite associée vers le point idéal \(I_{dl}\). En effet, si la feuille principale est bien représentée dans la correspondance de Beltrami, les suivantes s’enroulent sur quelques pixels dans le modèle KB.
• Ensuite placer un ou deux points sur la feuille précédente, pour voir que les points dans KB peuvent avoir une ordonnée positive, avec le changement des droites associées. Déplacer encore les points sur leurs cercles-parallèles respectifs. Observer le changement dans KB quand on franchit le méridien passant par X.
• Puis, avec les trois points sur la feuille principale, activer le changement de paramétrisation de la longitude, et explorer la figure pour voir que, selon les longitudes, le triangle \(A_{kb}B_{kb}C_{kb}\) ne se limite plus à la partie inférieure de l’horicycle rose.
Figure d’appropriation de la problématique du choix de la paramétrisation de la feuille principale
• Une fois ces premières explorations réalisées, on peut activer les points \(M, N, P\) qui sont des points sur les trois droites de KB. Ils sont renvoyés sur la pseudosphère en les points-retour \(M_r, N_r, P_r\). On a affiché aussi les coordonnées \((u, \theta)\) des ces trois points-retour.
• Comme signalé ci-dessus en préambule, ces points étant « sur objets » des droites, ils sont, en interne du logiciel, repérés barycentriquement à partir des points définissant les KB-droites. En particulier, si on change le choix de paramétrisation, un point-retour peut ne plus être sur la pseudosphère. Quand cela arrive, reprendre le point de KB concerné, et observer que son image sur la pseudosphère entre sur la surface au moment où le point de KB franchit l’horicycle rose.
• Faire parcourir ces points \(M, N, P\) sur leurs KB-droites et observer le parcours des points-retour \(M_r, N_r, P_r\) sur les droites de la pseudosphère, dans les deux cas de paramétrisation de la feuille principales.
• De nombreuses autres explorations sont possibles.
Complément sur les médiatrices
et le cycle circonscrit à un triangle
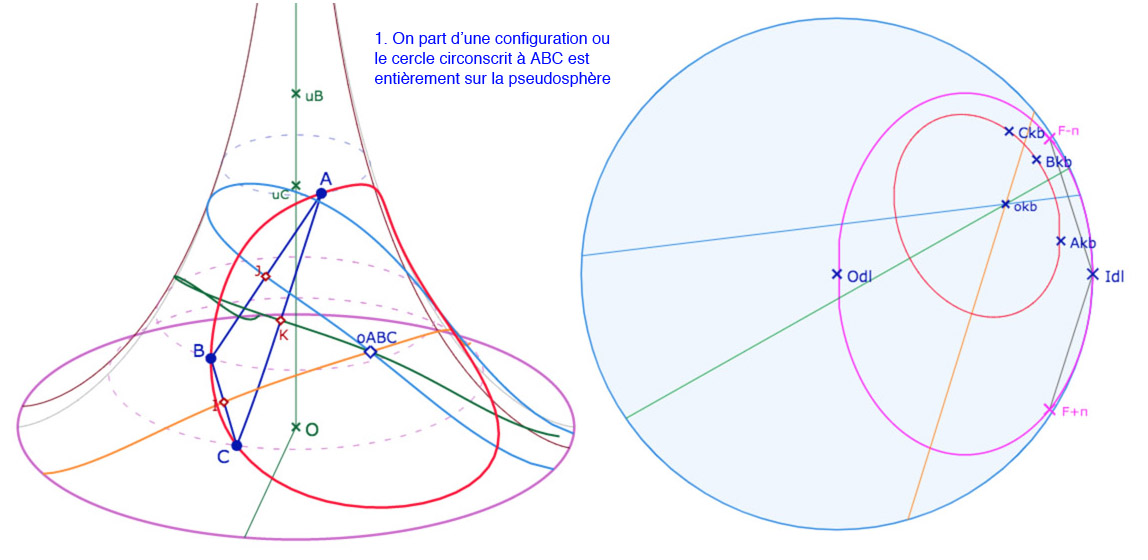
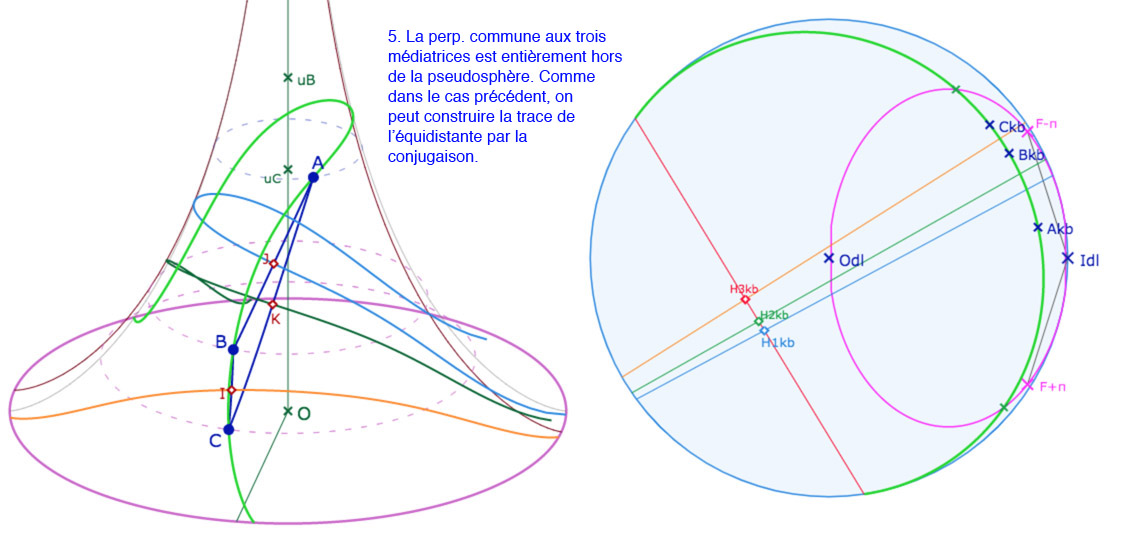
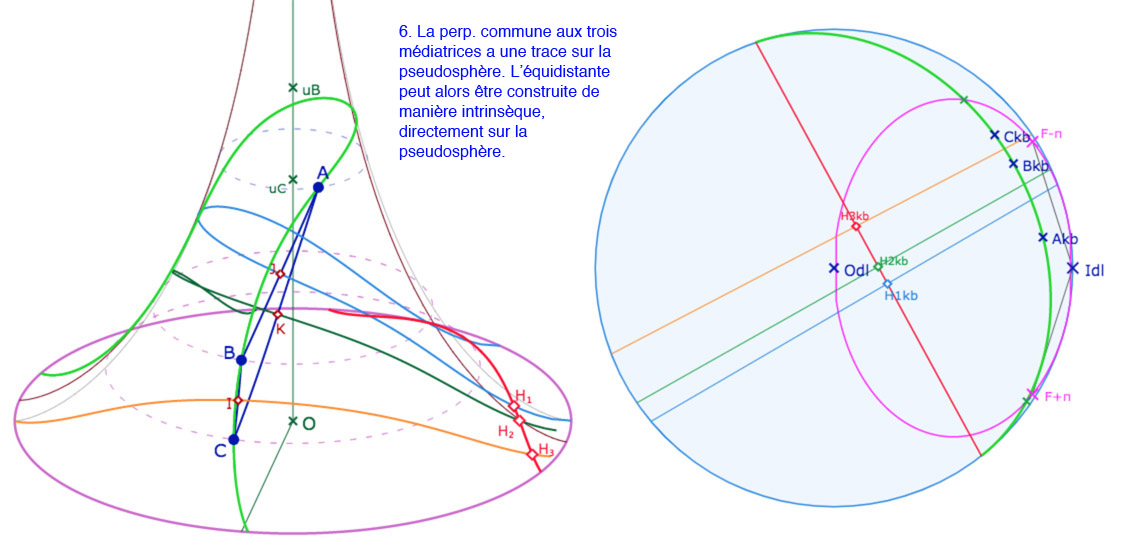
Nous avons déjà construit le cercle circonscrit à un triangle quand son centre appartient à la pseudosphère. Puis l’équidistante circonscrite à un triangle quand la perpendiculaire commune à ses médiatrices à une trace sur la pseudosphère. Mais les autres cas ne sont pas accessibles intrinsèquement sur la pseudosphère. La conjugaison avec KB permet de construire le cycle circonscrit dans toutes les configurations.
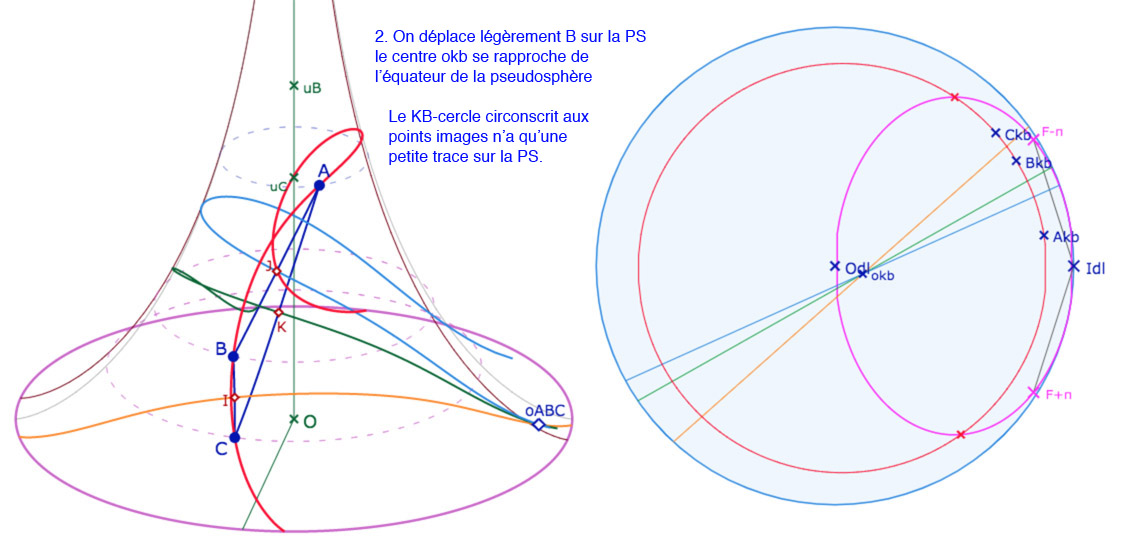
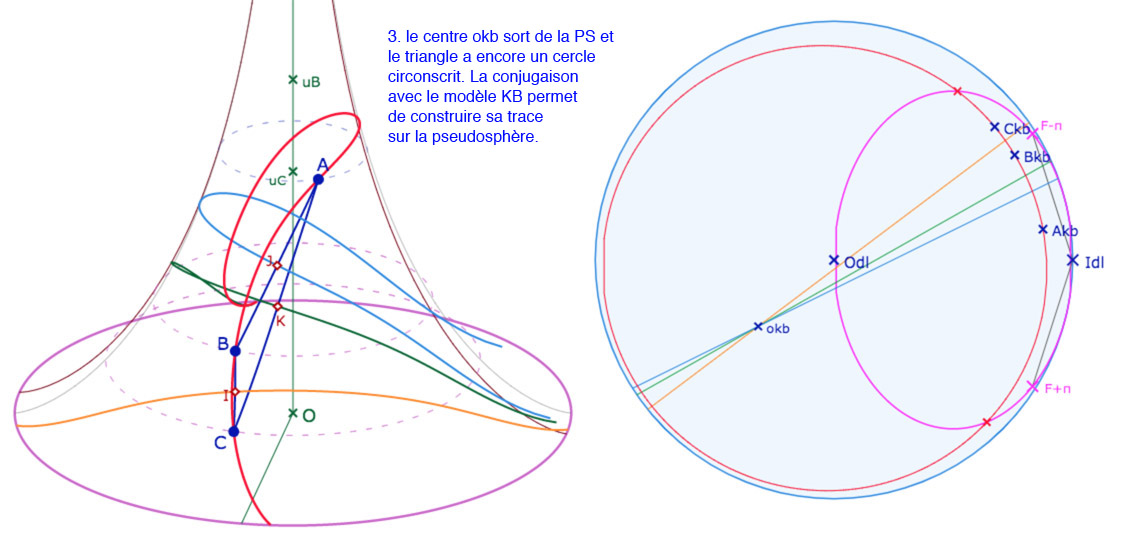
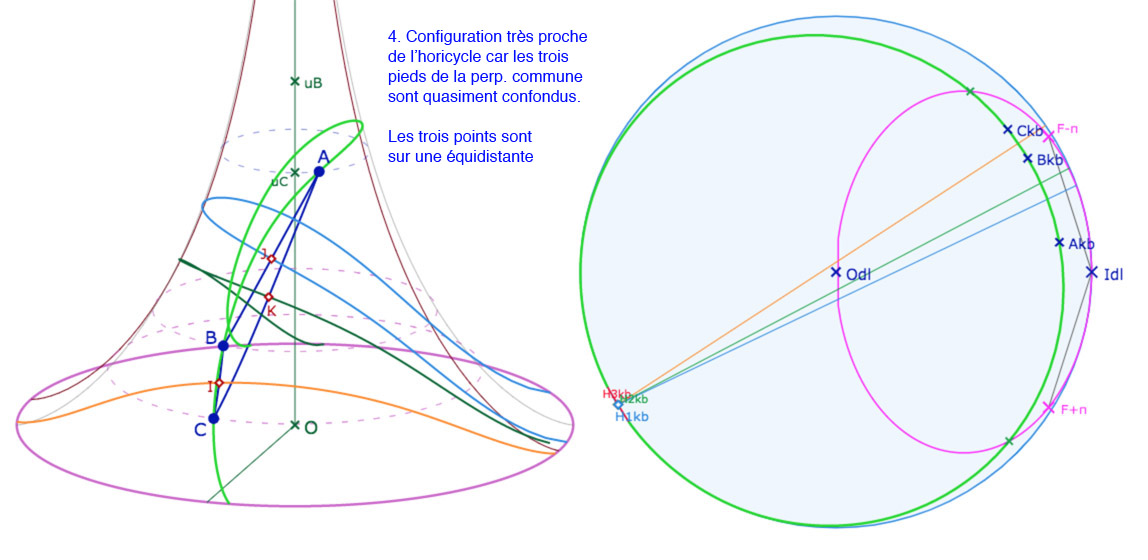
Ci-dessous on a choisi un triangle \(ABC\) de telle façon qu’un petit déplacement du point \(B\) permet de passer par toutes les situations que l’on souhaite illustrer. On continue de noter \(A_{kb}, B_{kb}, C_{kb}\) les images de \(A, B, C\) dans le disque-limite de Beltrami. Le point \(o_{kb}\) est l’intersection des KB-médiatrices du triangle dans KB. C’est l’image de l’intersection des médiatrices \(o_{ABC}\) si ce point existe sur la pseudosphère. De même on note \(H_{1kb}, H_{2kb}, H_{3kb}\) les intersections de la perpendiculaire commune aux médiatrices avec ces mêmes médiatrices, indépendamment de l’existence des points correspondants sur la pseudosphère. Le cycle circonscrit est tracé en rouge, dans KB et sur la pseudosphère quand c’est un cercle, et en vert, dans les deux modèles, quand c’est une équidistante. La différence est que, dans KB, les objets sont entiers et sur la pseudosphère, c’est souvent seulement la trace du cycle, sauf dans le cas où le cercle circonscrit est entièrement contenu dans la pseudosphère.
Galerie de 6 illustrations de la construction des traces sur la pseudsosphère des cycles circonscrits à un triangle.
La figure associée
Pour construire cette figure, il faut de nombreux outils, elle est donc assez longue à charger, et surtout à modifier. Toutes les configurations illustrées ci-dessus sont accessibles en déplaçant seulement \(B\) de quelques pixels. Pour alléger le chargement on a vidé la figure des nombreuses macros utilisées.
L’essentiel est donc dans le déplacement du point \(B\) d’à peine quelques pixels.
Préférer ouvrir la figure dans un nouvel onglet (un peu longue aussi à charger)