Quadrilatère à trois angles droits
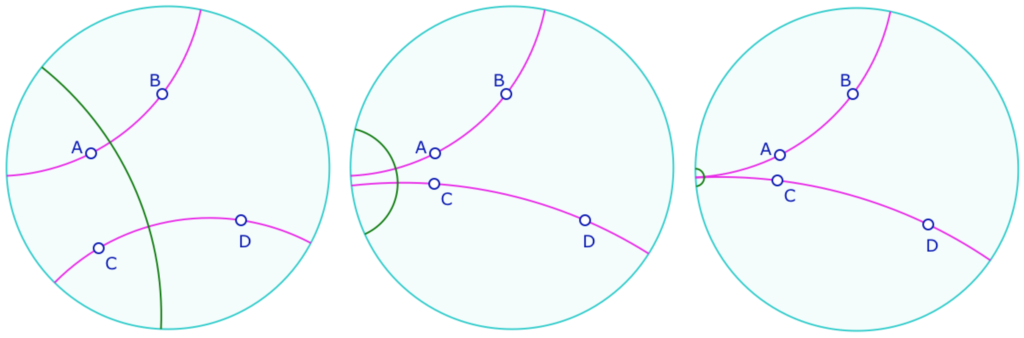
Soit une droite hyperbolique \((AB)\). Depuis un point \(N\), on construit :
• la perpendiculaire à \((AB)\) passant par \(N\).
• la perpendiculaire à cette droite issue de \(N\).
Puis on prend un point \(P\) sur cette dernière droite, et on construit une troisième perpendiculaire, à la dernière droite, passant par \(P\).
On a donc trois droites, avec trois angles droits, en \(N\), en \(P\) et en le point d’intersection non construit entre les deux premières droites. Dans le cas euclidien, cette configuration est celle du rectangle : il y a un quatrième angle droit, et les droites opposées sont parallèles.
Qu’en est-il ici ?
Quand on déplace \(N\), \(P\) va souvent «à l’infini» car la gestion de \(P\) comme « point sur objet » est euclidienne.
Il faut donc souvent reprendre le point \(P\) pour le ramener dans le disque.
Bilan : on observe donc que le quadrilatère peut ne pas fermer, selon les positions de \(P\) et \(N\), et que s’il se ferme, le quatrième angle n’est jamais droit : en géométrie hyperbolique, il n’existe pas de rectangle. Cela est dû au fait – ou selon le contexte, on observe – que dans un quadrilatère la somme des angles est inférieure à 360°. Il en résulte que dans un triangle, inférieure à 180°.
Perpendiculaire commune et parallélisme
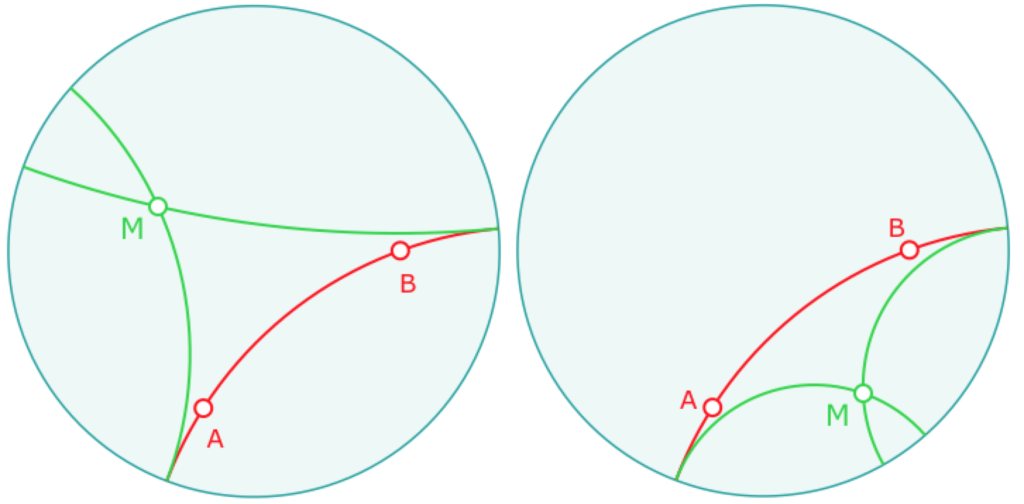
Dans la figure suivante, on se donne deux droites hyperboliques \((AB)\) et \((CD)\). On se place dans une situation où ces deux droites ne sont pas sécantes. On prend un point \(M\) sur \((AB)\). La perpendiculaire en \(M\) à \((AB)\) – droite bleue – coupe éventuellement \((CD)\) en \(N\). Puis on construit la perpendiculaire à \((CD)\)) en \(N\) – droite rouge.
Manipulation sur le figure : déplacer M sur la droite \((AB)\) et observer la situation.
Y a-t-il une position de \(M\) particulière. Que réalise- t-on alors dans ce cas ?
Dans le cas euclidien les deux droites non sécantes sont parallèles et ont une infinité de perpendiculaires communes,
d’où l’existence des rectangles. On a vu que ce n’est plus le cas ici, on cherche à préciser la situation.
On vient de voir que deux droites non sécantes ont, en général, une et une seule perpendiculaire commune. Il s’agit ici de préciser ce terme flou «en général».
Précisons que cela a été une question délicate car conceptuellement nouvelle. C’est celle sur laquelle Saccheri a buté en 1733. Après avoir découvert, avec une précision logique impressionnante, de nombreuses propriétés hyperboliques. Il a buté sur celle-ci en précisant que c’est impossible car «cela nuit à la nature de la droite». Il en conclu alors que Euclide est lavé de toute tâche, titre de son ouvrage sur le V° postulat d’Euclide, ouvrage redécouvert par Beltrami.
Dans cette figure on a construit la perpendiculaire commune aux deux droites \((AB)\) et \((CD)\).
1. Explorer finement, en déplaçant \(C\) ou \(D\) par exemple, cette phrase «en général deux droites non sécantes
ont une perpendiculaire commune» pour faire émerger la notion de droites parallèles.
2. Faire ensuite tourner \(D\) autour de \(C\). Combien y-a-t-il de parallèles à \((AB)\) passant par \(C\)?
(Très) bref aperçu historique
Saccheri a repris le quadrilatère de Al Kayan : un quadrilatère \(ABCD\) avec \([BC]\) et \([AD]\) à la fois égaux et orthogonaux à \([AB]\). Saccheri montre que les angles en \(C\) et \(D\) sont égaux. La question est de savoir s’ils peuvent être autre chose que droits. Il y a l’hypothèse de l’angle obtus (ce sera la géométrie elliptique) et celle de l’angle aigu (géométrie hyperbolique).
Il évacue très vite le cas elliptique car il montre que cela conduirait à ce que les longueurs des droites soient bornées. Un tel résultat n’était pas acceptable à cette époque, contraire à une demande de base de la géométrie d’Euclide, à savoir que l’on peut prolonger indéfiniment un segment. Il faudra attendre Riemann pour que cela soit considéré comme recevable. Nous sommes donc sur l’hypothèse de l’angle aigu. Saccheri montre que la somme des angles d’un triangle est inférieure à 2 droits, une propriété sur la projection orthogonale du milieu, et surtout il montre l’unicité de la perpendiculaire commune à deux droites non sécantes. Saccheri a alors, sans aucun modèle bien entendu, simplement par sa démarche logique, la vision claire de ce que vous avez pu observer sur la figure précédente : la perpendiculaire commune semble aller vers l’infini quand les droites (\((AB)\) et \((CD)\) se rapprochent de la situation «sécantes».
Et Saccheri conclut, de manière surprenante, après tant de précautions logiques, et de réussites, que cette situation «nuit à la nature de la droite». Et n’a donc pas vu (voulu voir ?) le parallélisme hyperbolique : le cas où deux droites ne sont pas sécantes mais n’ont pas non plus de perpendiculaires communes.
Le parallélisme hyperbolique comme situation non connectée
La grande difficulté conceptuelle – pour l’époque de Saccheri – est d’imaginer que deux droites puissent être «non connectables», c’est-à-dire qu’on ne puisse passer de l’une à l’autre par un point commun ou une perpendiculaire commune. On verra – dans la page sur la séparation des géométries du menu consacré à l’axiomatique de Bachmann – qu’un plan euclidien est un plan dans lequel il existe un rectangle (deux droites admettent deux perpendiculaires communes), et tel que toutes les droites sont connectables.
Au contraire, une situation est dite hyperbolique s’il existe des droites non connectables, et un plan hyperbolique est – dans l’axiomatique de Bachmann – un plan dans lequel par un point \(P\) n’appartenant pas à une droite \(d\), il existe deux – et deux seulement – droites passant par \(P\) et non connectables à \(d\), c’est-à-dire deux droites passant par \(P\) et parallèles à \(d\).
Dès ses premiers travaux sur la géométrie hyperbolique, Bolyaï appelait déjà bouts les points à l’infini communs à deux droites parallèles, terme repris par Hilbert. C’est une notion importante pour travailler la transitivité. En effet, en géométrie hyperbolique, il n’y a pas transitivité du parallélisme des droites sauf si elles ont le même bout.
Dans le vocabulaire de Bachmann, on dira que deux droites ont soit un point soit une perpendiculaire commune, soit qu’elles sont sans support.
Étendre ces notions à trois droites, avec des axiomes sur les deux cas connectables, et montrer la transitivité de ce concept dans tous les cas, y compris celui sans support, avec aucun axiome sur ce cas particulier est un des premiers enjeux de son axiomatique.
Dans le dernier item de ce menu, nous allons explorer ces questions, essentiellement de manière heuristique.
Droites en pinceaux
Deux options pour cette première approche des droites en pinceaux :
• soit faire soi-même la figure – c’est très simple – c’est ce qui est proposé ci-après.
• soit préférer manipuler la figure finalisée (s’ouvre dans un autre onglet).

Parce que c’est intéressant de faire soi-même la manipulation, nous proposons au lecteur, dans la figure suivante de faire une petite manipulation toute simple sur la figure, pour construire les perpendiculaires communes aux hauteurs de trois droites prises deux à deux. (Réviser la pratique des macros sur cette page.)
Pour cela activer le mode macro (icone marteau clé-à-molette) et choisir Perp commune. La macro attends 3 objets. On montre d’abord le cercle horizon, puis deux hauteurs. Pour que cela soit pertinent suivre la feuille de route proposée ci-dessous.
Les hauteurs (droites vertes) d’un triangle ABC (droites rouges) – Cas «non sécantes».
1. Activer le mode macro (marteau – clé) – Tracer la perpendiculaire commune des hauteurs issues de \(A\) et \(B\).
2. Quitter le mode macro en activant l’inspecteur d’objets (la roue). Sélectionner la perpendiculaire commune et la colorier en bleu
3. Reprendre le mode macro. Tracer maintenant la perpendiculaire commune des hauteurs issues de \(B\) et \(C\).
4. Déplacer \(B\) par exemple. Que remarque-t-on ? Que peut-on conjecturer ?
Dans la figure précédente on a vérifié, sur le modèle de Poincaré, que, quand elles ne sont pas sécantes, les hauteurs d’un triangle ont une perpendiculaire commune aux trois hauteurs.
On a déjà vu – là encore expérimentalement – que quand elles sont sécantes, les trois hauteurs sont concourantes, et donc par disjonction des cas, quand elles sont sans point commun, ni sans perpendiculaire commune, elles sont toutes les trois parallèles, ce que l’on peut dire aussi comme ayant un point idéal en commun (le bout de Bolyaï et Hilbert) : le point à l’infini que l’on peut observer sur une illustration précédente.
Autrement dit, les hauteurs d’un triangle ont quelque chose en commun : un point hyperbolique, une perpendiculaire, ou encore – le cas «sans support» des droites parallèles – un point idéal.
Droites en pinceau – approche heuristique, opérationnelle
Quand trois droites ont quelque chose en commun, on dira qu’elles sont en pinceau. Et on précisera la typologie «à centre», «à axe» ou «sans support» selon que les droites sont concourantes, ont une perpendiculaire commune, ou sont parallèles.
Avec ce simple vocabulaire, accepté comme consistant, et le fait que ces trois situations sont disjointes, on peut arriver à faire des démonstrations qui correspondent à des ilots de cohérence comme on peut en faire collège, sur quelques définitions précises, même si l’axiomatique générale n’est pas très précise.
Droites en pinceau – aspect théorique
Dans l’axiomatique de Bachmann, les objets premiers sont les symétries orthogonales (dans un groupe). Les droites ne sont que des représentations de ces isométries. On fait parfois «du Bachmann» à l’école primaire, quand, pour décrire ce qu’est une droite à partir d’un pliage, on fait plier une feuille à un élève et qu’on lui demande de «dessiner le trait» avec un crayon.
Dans ce contexte, trois droites sont «en pinceau» si le produit des trois est une droite. Autrement, d’un point de vue géométrique, si la composée des trois symétries orthogonales associées est encore une symétrie orthogonale.
Qu’en est-t-il des médiatrices ? des médianes ?
Là encore on propose à l’utilisateur de finaliser lui-même la figure. On peut ne pas colorier les perpendiculaires communes aux médiatrices et juste s’apercevoir qu’elles coïncident. Comme à la figure précédente, on peut aussi préférer ouvrir et manipuler, dans un nouvel onglet, la figure finalisée.
Dans tous les cas le premier objet à montrer pour une macro est le cercle horizon.
1. Activer le mode macro, et construire les 3 médiatrices du triangle. Puis placer le triangle pour qu’elles soient non sécantes.
2. Comme pour les hauteurs prendre la perpendiculaire commune à deux médiatrices, puis changer la couleur.
3. Construire ensuite la perpendiculaire commune à un autre couple de médiatrices. Conjecture ?
4. En utilisant la macro «intersection de deux droites», construire les milieux des côtés, puis les médianes du triangle. Conjecture ?
Donc, comme les hauteurs, les médiatrices sont aussi en pinceau. On l’admet désormais comme un résultat acquis, utilisable.
De même, dans la figure précédente, vous avez pu expérimenter que les médianes sont, elles, toujours en pinceau à centre – c’est-à-dire concourantes. Que les médianes soient dans un pinceau toujours «à centre» est un résultat théorique assez délicat à montrer dans le cas général de la géométrie hyperbolique . On peut bien entendu le montrer, géométriquement, avec l’inversion, dans le modèle du disque de Poincaré mais cela ne prouve rien du cas hyperbolique en général.
Un premier théorème absolu
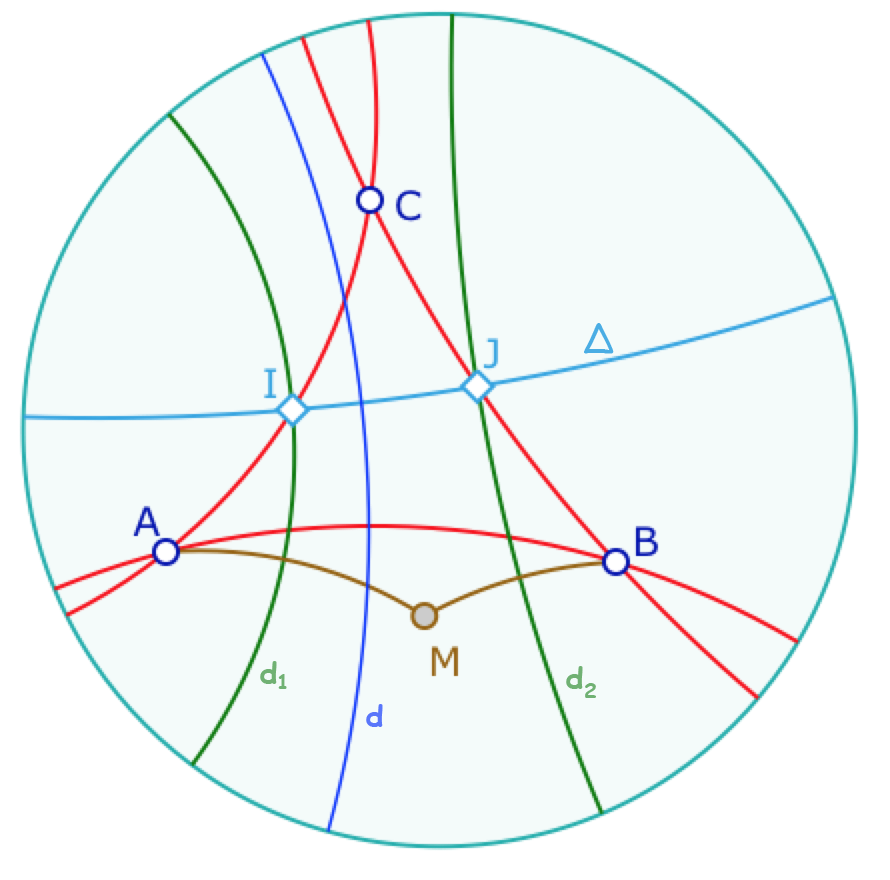
Avec ce résultat sur les médiatrices et de quelques données supplémentaires nous allons démontrer un premier résultat. Pour cela, on suppose acquis que toute symétrie centrale de centre \(I\) est la composée de deux symétries orthogonales d’axes orthogonaux en \(I\) et que cette écriture, comme dans le cas euclidien, est commutative.
(ci-contre \(s_{I} = s_{d_1} ∘ s_\Delta = s_\Delta ∘ s_{d_1}\)). Ce ne sont que des propriétés algébriques sur les éléments d’ordre 2 dans un groupe.
Soient \(ABC\) un triangle, \(I\) et \(J\) les milieux de \([AC]\) et \([BC]\). On note \(\Delta\) la droite \((IJ)\), \(d_1\) et \(d_2\) les perpendiculaires à \(\Delta\) en \(I\) et \(J\) respectivement. Soit \(M = s_{d_1}(A)\) le symétrique de \(M\) par rapport à \(d_1\). Par \(I\) milieu de \([AC]\) et \(J\) milieu de \([BC]\), on a \(A = s_I(C) = s_I ∘ s_J(B)\).
Or \(s_I ∘ s_J = (s_{d_1} ∘ s_\Delta) ∘ (s_\Delta ∘ s_{d_2}) = s_{d_1} ∘ s_{d_2}\) et donc on peut écrire \(A = s_{d_1} ∘ s_{d_2}(B)\), soit \(M = s_{d_1}(_{d_1} ∘ s_{d_2}(B)) = s_{d_2}(B)\). et donc \(M\) est aussi le symétrique de \(B\) par rapport à \(d_2\).
Ainsi, dans le triangle \(AMB\), \(d_1\) et \(d_2\) sont deux médiatrices du triangle, toutes les deux orthogonales à la droite \(\Delta\). Donc dans le triangle \(AMB\), les médiatrices sont en pinceau à axe. Et donc la troisième médiatrice du triangle, la droite \(d\) ci-dessus est, elle aussi, perpendiculaire à \((IJ)\), Il y a là clairement un résultat spécifique. Alors quel est le théorème que l’on vient de démontrer ?
Cette question a été posée, plusieurs années de suite, en formation initiale des enseignants, dans un contexte d’homologie didactique. L’idée est de transposer un théorème élémentaire pour les étudiants, mais dans un contexte non usuel, pour illustrer que, même sur des choses très simples, ils peuvent, comme leurs élèves, sentir que quelque chose a été démontré en ayant des difficultés pour exprimer clairement ce qui a été démontré : quelle est l’expression absolue du théorème des milieux ?
Théorème absolu de la droite des milieux
Les trois droites \(d_1, d_2\) et \(d\) sont en pinceau à axe. Le fait que la droite des milieux \((IJ)\) et le côté \((AB)\) ont une perpendiculaire commune n’est pas vraiment une information, cela signifie – ici dans le contexte hyperbolique – seulement qu’elle ne sont pas sécantes. Par contre le fait que ces deux droites admettent la médiatrice de \(A\) et \(B\)comme perpendiculaire commune est une information, et c’est cela le théorème absolu des milieux.
On peut remarquer que la preuve apportée ici est absolue, au sens où cela ne fait intervenir que des arguments géométriques abstraits et n’utilise aucune spécificité du modèle dans lequel on l’illustre.
Une fois ceci observé, on peut préciser que si on exprime le résultat avec «la perpendiculaire commune» le résultat ne va être que hyperbolique, car dans le cas euclidien il n’y a pas unicité de la perpendiculaire commune de deux droites. Pour contenir aussi le cas euclidien, on peut dire :
Théorème – Dans un triangle, la droite des milieux de deux côtés et le troisième côté admettent comme perpendiculaire commune la médiatrice du troisième côté.
Comme ce théorème est rédigé, il est absolu – au sens usuel, soit euclidien et hyperbolique – et donc, dans le cas euclidien, il se traduit par le fait que les droites \((IJ)\) et \((AB)\) sont parallèles.
Prospective ou superposition culturelle : on verra dans le menu sur la géométrie elliptique que cette preuve s’applique aussi dans cette géométrie car si trois droites sont «en pinceau à axe», elles sont aussi «en pinceau à centre». Et dans ce cas, le théorème se traduit aussi par l’alignement des milieux comme déjà mentionné dans la page de présentation sur les modèles pour parler de l’ambiguïté de l’interprétation des résultats dans les modèles.
Ainsi rédigé, il est absolu au sens de Bachmann, c’est-à-dire vrai dans les trois géométries classiques, elliptique, euclidienne et hyperbolique.