Avant d’aborder à l’item suivant un exemple de modèle hyperbolique fini, précisons quelques définitions sur l’aspect géométrique des configurations finies en vu de réaliser quelques illustrations dynamiques finies.
Dans cette introduction, on entend par géométrie, la donnée d’un triplet \((P, D, I)\) où \(P\) est l’ensemble des points, \(D\) celui des droites et \(I\) est une partie de \(P \times D\) qui décrit l’incidence : \(A I d\) se lit «\(A\) est un point de \(d\)» ou «\(d\) passe par \(A\)». Dans cette page \(D\) est tout simplement un sous ensemble des parties de \(P\) et l’incidence est alors l’appartenance d’un point à une droite.
Les configurations planes abstraites
On appelle configuration plane abstraite (CPA) de paramètre \((p_n,d_m)\) une géométrie qui vérifie les axiomes suivants :
CP1. La configuration contient \(p\) points et \(d\) droites. Par chaque point il passe \(n\) droites et chaque droite contient \(m\) points.
CP2. Deux points distincts sont, au plus, sur une même droite.
CP3. Des droites se rencontrent en au plus un point.
CP4. La géométrie est connectée.
Dans une telle configuration, il est facile de vérifier que\(pn=dm\) . L’axiome 2 signifie surtout qu’il n’existe pas nécessairement une droite passant deux points, l’axiome 3 qu’il peut y avoir des droites parallèles et l’axiome 4 qu’il y a toujours un trajet, par des droites, pour aller d’un point à un autre.
Vocabulaire associé
Quand un modèle d’une configuration est réalisable avec des segments du plan euclidien usuel pour représenter l’alignement des points, on parle de configuration plane. L’adjectif abstrait n’est ajouté que dans le cas où l’une des droites de la configuration ne peut en aucun cas être une droite.
Quand, dans une configuration, il y a le même nombre de points que de droites \((p=d)\), alors il y a le même nombre de points par droites et de droites passant par un point \((m=n)\), on parle alors de configuration \(p_n\).
Exemple du quadrilatère complet
C’est une configuration (62,43) : 6 points et 4 droites, 2 droites passent par chaque point, et chaque droite contient 3 points.
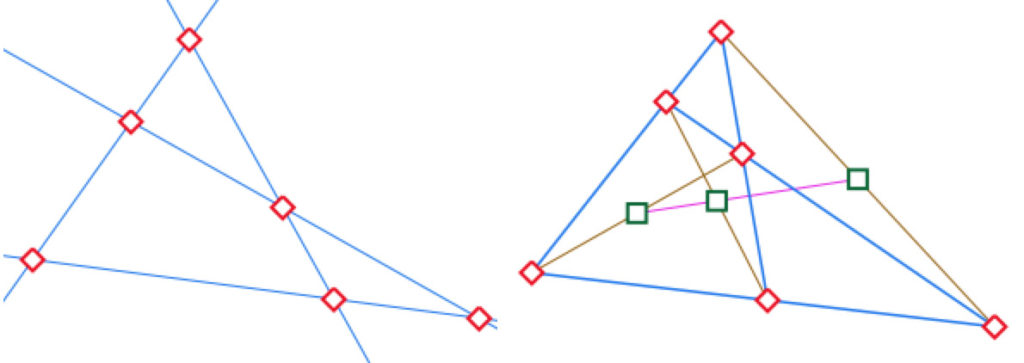
Si on construit la droite de Newton du quadrilatère complet, la droite des milieux des diagonales (les trois points sont alignés dans un contexte affine), on ajoute 4 droites et 3 points : les trois diagonales marrons et les trois milieux verts, alignés, ce qui donne une droite supplémentaire.
Ainsi sur l’illustration de droite, on a 9 points et 8 droites, cela n’est donc pas une configuration car
• d’une part, par certains points il passe 3 droites et par d’autres 2 droites.
• d’autre part, 9 et 8 étant premiers entre eux, pour avoir une configuration, il faudrait 8 droites par point et 9 points par droite.
Les configurations finies affines et projectives
Les axiomes affines
Aff1. Par deux points il passe une et une seule droite.
Aff2. Par un point n’appartenant pas à une droite, il passe une et une seule droite par ce point ne rencontrant pas la droite.
Aff3. Il existe trois points qui ne sont pas tous contenus dans une droite.
Les axiomes projectifs
P1. Par deux points il passe une et une seule droite.
P2. Deux droites distinctes sont sécantes en un unique point.
P3. Il existe 4 points tels que trois d’entre eux ne sont jamais incidents à une même droite.
Dans le cas affine, si une droite a \(n\) points, toutes les droites ont \(n\) points, il y a \(n^2\) points. Par chaque point il passe \(n+1\) droites, il y a \(n^2+n\) droites. Le plan affine d’ordre \(n\) est une configuration\(\left(n^2_{n+1},(n^2+n)_n \right)\).
Un plan projectif d’ordre \(n\) est une configuration\(\left((n^2+n+1)_{n+1} \right)\).
Le plan de Fano
C’est le plus petit plan projectif, le plan d’ordre 2, c’est-à- dire le plan à 7 droites de 3 points chacune. C’est aussi la seule configuration 73. Cette configuration est la plus célèbre, elle est abstraite car une droite est représentée par un cercle. Il n’existe pas de représentation du plan de Fano avec seulement des segments, mais on en verra une avec des triangles.
Utilisation : en déplaçant les deux points \(A\) et \(B\), la droite \((AB)\) est dessinée
en trait plein (segment ou cercle). Le troisième point de la droite est le point \(I\).
Techniquement, les points \(A\) et \(B\) sont aimanté par les points du plan projectif : on travaille ainsi de manière dynamique sur une géométrie finie.
Ci-contre le plan affine d’ordre 2 avec 4 points et 6 droites. Observer qu’il est bien affine, en particulier vérifie Aff2, l’axiome d’Euclide. On montre qu’en dehors de ce cas trivial, les plans finis, affines ou projectifs, n’ont pas de modèles de type «configuration plane», elles sont nécessairement abstraites comme ci-dessus.
Les configurations de Pappus et Desargues
Deux configurations fondamentales
Avant d’aborder le plan affine suivant, à 9 points et 12 droites, il existe deux «configurations planes», au sens ci-dessus importantes, intermédiaires – en nombre de droites – ce sont les célèbres configurations de Pappus et de Desargues.
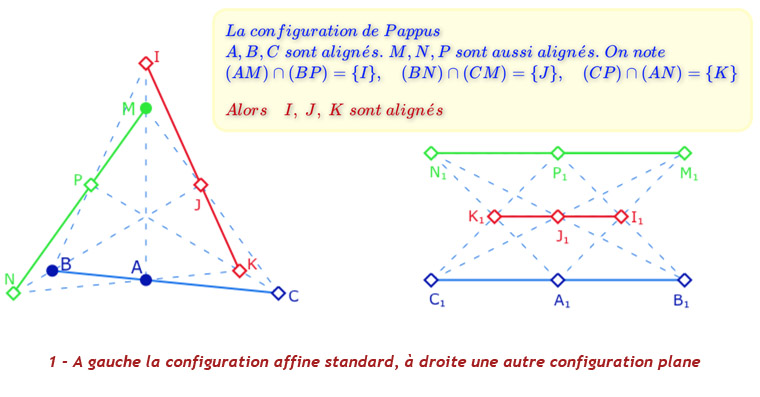
La configuration de Pappus
C’est l’une des trois configurations de type 93 soit 9 droites et 9 points, avec 3 points par droites et trois droites par point. Dans l’approche axiomatique, on sait que la présence de la configuration de Pappus induit que le corps de nombres construit est commutatif.
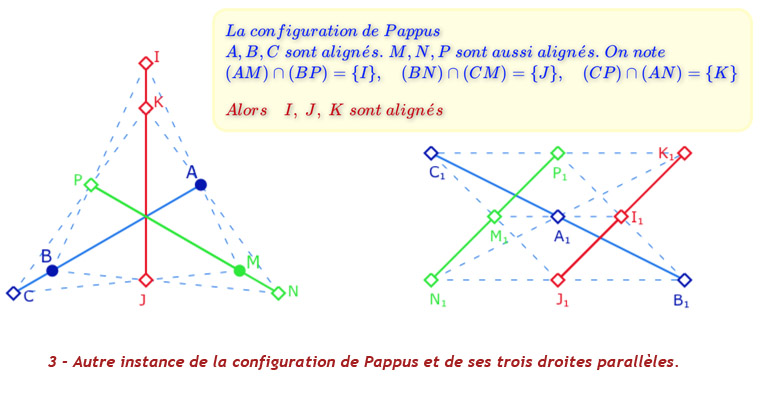
Avant de manipuler cette figure dans sa version de « géométrie dynamique finie » voici trois illustrations où l’on voit les trois ensembles de trois droites parallèles.
La figure dynamique
On remarquera que sur la configuration de gauche, il y a trois trois cercles implicitement utilisés pour la construction. Ce seront les trois droites parallèles qui manquent pour avoir un plan affine, car la configuration de Pappus n’est pas une configuration d’incidence.
On déplace les deux points \(A\) et \(B\) sur la configuration de gauche.
Le point \(A\) ne peut se déplacer que sur les 3 points les plus proche du centre de la figure
et \(B\) sur les 6 autres , les plus à l’extérieur, ce qui limite (avec \(M\)) l’exploration à 36 cas sur les 108 possibles.
Le point \(M\) peut toujours prendre deux positions une sur chacune des deux droites possibles pour la droite \((MN)\).
La configuration de Desargues
C’est l’une des dix configurations de type 103. Donc dix points dix droites, trois droites par point, trois points par droite. Sa symétrie signifie que tout point de la configuration peut être tout point des hypothèses, y compris le point I qui pourrait paraître spécifique.
C’est une configuration fondamentale car sans elle il n’y pas de coordonnées cohérentes possibles. Cette configuration est une conséquence de l’existence de l’espace et des plans dans l’espace. Donc la question de son existence n’est posée que dans le cas du plan. Le menu Non Arg propose d’explorer deux modèles euclidiens de géométrie plane non arguésienne, un modèle de Hilbert et le plan de Moulton.
Déplacer le point \(I\) sur l’un des 10 points possibles de la configuration
Le plan affine d’ordre 3 (9 points et 12 droites)
Si une des motivations de cette page est de préparer la présentation d’un plan hyperbolique fini (menu suivant), une autre raison est le thème de cette section : le plan affine d’ordre 3. En effet, on observera en géométrie hyperbolique que les médianes sont toujours concourantes, ce sera trivialement vrai dans le cas elliptique, et on sait que c’est vrai dans le cas euclidien. Et pourtant, dans l’axiomatique de Bachmann, pourtant si riche et si puissante, il n’est pas possible de démontrer ce résultat dans le cas général, avant la séparation des géométries. La raison en est très simple : L’axiomatique de Bachmann contient aussi, en puissance, les cas finis euclidiens. Or il y a un cas, un seul, où ce résultat n’est pas vrai : sur un corps de caractéristique 3 et donc, pour le cas le plus simple, dans ce plan à 9 points, car c’est la géométrie affine standard sur le corps \(\displaystyle \frac{\mathbb{Z}}{3\mathbb{Z}}\). Avant de construite les médianes d’un triangle, déjà observons comment passer de la configuration de Pappus à ce plan affine.
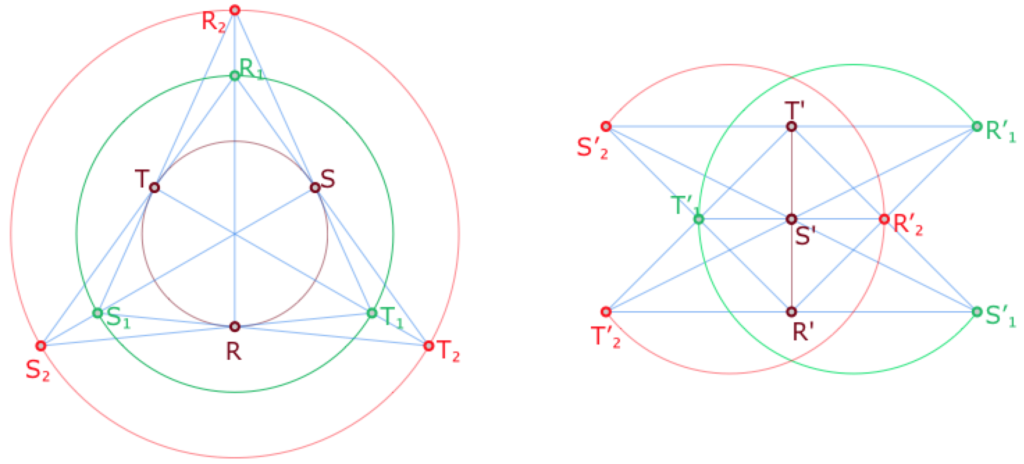
Nous avions 9 points et 9 droites, il manque trois droites, parallèles, ce sont celles qui passent respectivement par \(R, S, T\), puis \(R_1, S_1, T_1\), et \(R_2, S_2, T_2\), représentées par trois cercles à gauche, un segment et deux arcs de cercles à droite.
La configuration de droite est celle qui contient le plus grand nombre possible de segments. Celle de gauche est la suivante. Mais ce ne sont pas, non plus, les modèles les plus simples.
Comme nous ne sommes pas en caractéristique 2, la structure étant affine, les milieux existent. Ainsi, sur une droite, tout point est milieu des deux autres.
Les médianes d’un triangle
Ces configurations finies posent la question des représentations d’une notion aussi simple que celle de segments. Ainsi, le milieu d’un segment \([AB]\), dans une structure affine, par barycentre, doit être entre les deux points. Mais dans le cas fini, il n’y a pas d’ordre, comment le représenter ? Quelle collusion entre la représentation dans le modèle euclidien et la réalité de l’objet mathématique ? En fait une bonne représentation serait celle sur un tore, mais on ne serait plus dans une configuration plane.
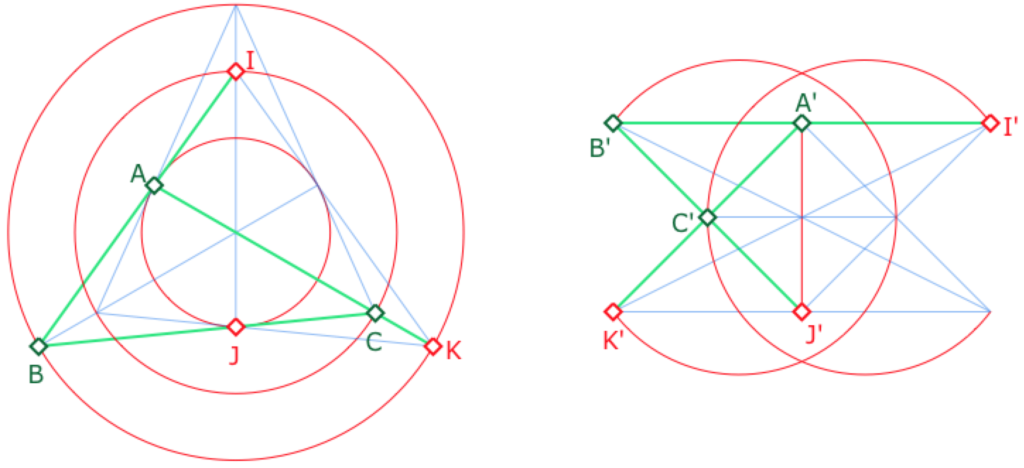
Voici quelques exemples de triangles \(ABC\) et de leurs médianes \((CI), (AJ)\) et \((BK)\). Dans l’illustration ci-contre, on a tracé les droites du triangle. Seul \(J\) est, dans le modèle, entre \(B\) et \(C\) (à gauche, mais pas à droite).
Les trois médianes, comme droites, sont alors les trois cercles ajoutés à la configuration de Pappus pour faire un plan affine. Ce sont trois droites parallèles : dans ce triangle, les médianes sont parallèles.
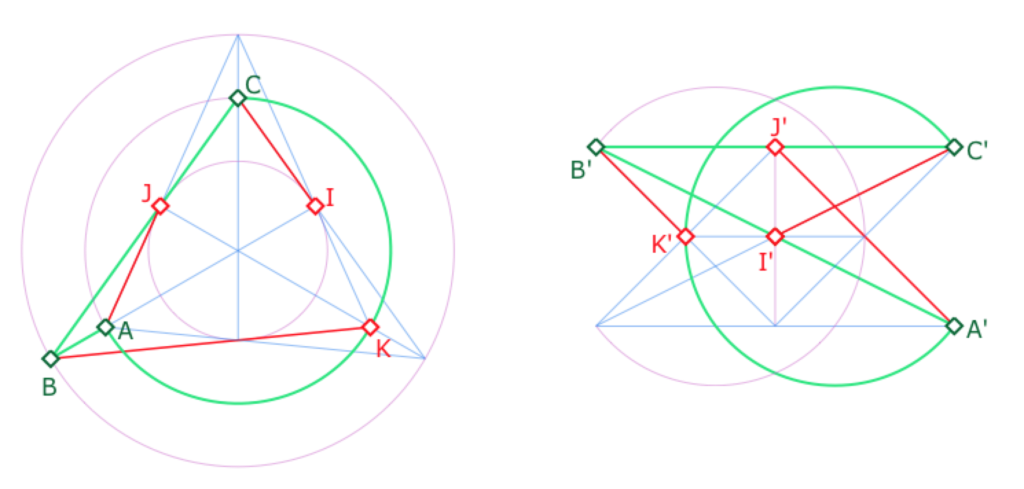
Dans cette autre illustration, on a tracé les trois segments \([AB]\), \([BC]\) et surtout \([CA]\), qui est un arc de cercle dans la configuration de gauche et la droite toute entière dans celle de droite.
Pour les médianes, on a aussi choisi de tracer les segments . Ils sont encore sur des droites parallèles. On peut déjà envisager de conjecturer que, pour ce plan, les médianes sont toujours parallèles.

Pour ce troisième exemple, dans le modèle de gauche, on a tracé les trois segments \([AB]\) (arc de cercle), \([BC]\) et \([CA]\), ces deux derniers étant les droites toutes entières. Les médianes sont deux droites et un segment. Elles forment un troisième faisceau de droites parallèles.
Le modèle de droite ne respecte les mêmes rapports aux droites et segments. Nous avons abordé brièvement cette question car elle sera à nouveau soulevée avec le cas elliptique, différemment, mais pour des raisons identiques : la géométrie elliptique est elle aussi non orientable.
Preuve du parallélisme des médianes
D’une manière générale on se pose la question dans une structure affine, considérée d’un point de vue algébrique comme issue d’une structure vectorielle. On cherche à savoir quand les vecteurs \(\overrightarrow{AI}\) et \(\overrightarrow{BJ}\) sont colinéaires ce qui revient à comparer les vecteurs \(\overrightarrow{AB}+\overrightarrow{AC}\) et \(\overrightarrow{BA}+\overrightarrow{BC}\). Or, par Chasles, on peut écrire \(\overrightarrow{BA}+\overrightarrow{BC}=-2\overrightarrow{AB}+\overrightarrow{AC}\).
Et donc ce vecteur n’est colinéaire avec \(\overrightarrow{AB}+\overrightarrow{AC}\) que si \(-2\overrightarrow{AB}=\overrightarrow{AB}\), soit que si \(-2=1\) et donc que si on est en caractéristique 3. Et réciproquement dans ce cas c’est toujours vrai, les médianes sont toujours parallèles.
Dans l’axiomatique de Bachmann, on montre que les médianes sont toujours en faisceau, ce qui signifie, pour le cas euclidien, qu’elle peuvent être parallèles ou concourantes. C’est ce point qu’il n’est pas possible de trancher dans le cas général : cette section est consacrée à ce cas particulier qui ne permet pas de conclure à un résultat plus général.
La structure euclidienne
Un plan affine sur un corps est naturellement muni d’une structure euclidienne. C’est donc le cas de cette configuration. C’est même la plus petite qui est possible par l’axiomatique de Bachmann, car, dans ses 5 axiomes, le 5° est un axiome de non dégénérescence, qui demande à ce que la structure ait au moins un triangle rectangle. Or dans ce plan à 9 points non seulement il existe un triangle rectangle, mais tous les triangles de ce plan sont rectangles : la structure n’est pas assez riche pour qu’il y ait autre chose.
Pour voir cela, commençons dans un premier temps, par un autre modèle de cette configuration. Elle est plus classique que les précédentes, en particulier, elle est « conforme » c’est-à-dire que les angles que l’on voit dans le modèle euclidien sont les angles de la géométrie. Les points sont les 9 points d’une grille 3×3. Les droites sont les lignes horizontales, verticales, les deux diagonales principale et les quatre diagonales secondaires : dans l’illustration de gauche ci-dessous, on a représenté la droite \((AB)\), avec son point \(I\), milieu de \(A\) et \(B\).
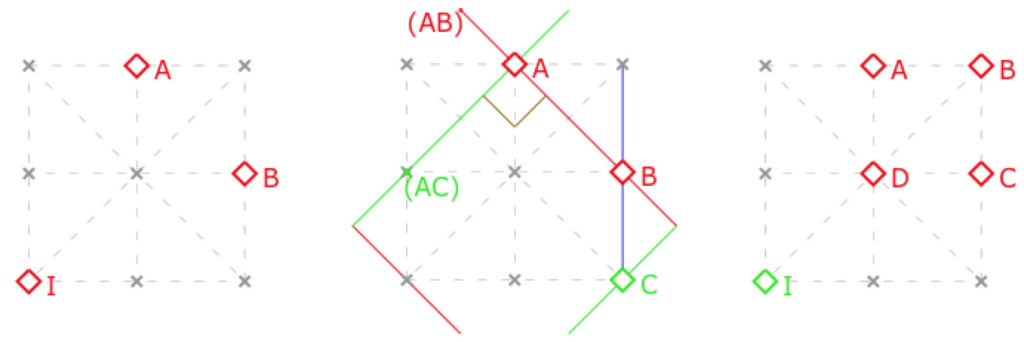
à gauche, \(I\) milieu de \([AB]\), au centre le triangle \(ABC\) rectangle en \(A\),
à droite le carré et le cercle \(ABCD\) tous les deux de centre \(I\).
Dans ce modèle, il est plus clair de voir qu’en chaque point, on peut regrouper les deux paires de droites en paires de droites orthogonales (par exemple en décomposant la symétrie centrale en un point en deux symétries orthogonales d’axes orthogonaux).
Sur l’illustration centrale, le triangle ABC est un triangle rectangle en A, car \((AB)\) et \((AC)\) sont orthogonales. Tous les triangles de cette géométrie sont de cette forme. De même un cercle est constitué de 4 points, et ces 4 points forment un carré. C’est le cas, dans l’illustration de droite, du cercle de centre \(I\) passant par \(A\), ABCD est à la fois les 4 points de ce cercle, et aussi un carré de centre I.
Le centre du cercle circonscrit au triangle \(ABC\) (au centre) est le milieu de l’hypoténuse \([BC]\) donc le troisième point de la droite \((BC)\), en bleu.
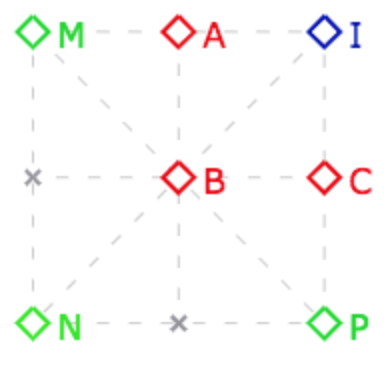
Caractéristique 3 : quand la symétrie centrale est aussi l’homothétie de rapport 2
Dans cette illustration, le triangle \(MNP\) est à la fois l’homothétique de \(ABC\) dans l’homothétie de centre \(I\) et de rapport 2. Mais c’est aussi le symétrique de \(ABC\) dans la symétrie centrale de centre \(I\) : c’est une autre illustration de l’égalité \(2=-1\).
Les droites parallèles ont des perpendiculaires communes. Dans les illustrations de la section précédente, on en déduit que les perpendiculaires communes aux droites représentées par les trois cercles sont les droites, comme \((BK)\), passant par le centre de la figure. De même les autres paires de perpendiculaires sont les droites comme \((BC)\) et (\((IJ)\) qui forment deux triplets de droites parallèles orthogonales deux à deux : les parallèles à \((BC)\) sont perpendiculaires aux parallèles à \((IJ)\).
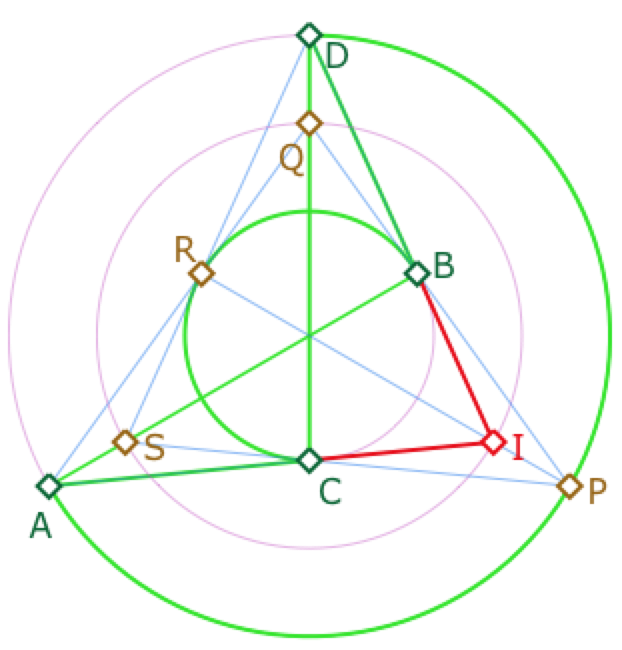
Dans ce modèle, ci-contre le carré ABCD de centre I, milieu des diagonales \([AC]\) et \([BD]\). On voit bien que les droites \((BC)\) et \((DA)\) – représentée par l’arc de cercle pour une meilleure lisibilité – sont perpendiculaires en \(B\). (BC) est bien entendu perpendiculaire aussi à \((CD)\), parallèle à \((AB)\). De même, on sait que \((AI)\) est parallèle à \((PQ)\) et on a dit que \((PQ)\) et \((DI)\) sont perpendiculaires en \(B\). Donc les diagonales \((BD)\) et \((AC)\) sont aussi orthogonales en \(I\).
De même, le quadrilatère des milieux PQRS est aussi un carré de centre I car \(I\) est milieu de \([RP]\) et de \([QS]\), représenté par un arc de cercle, non dessiné ci-contre. Ces deux diagonales sont à nouveau, orthogonales en \(I\). On a donc une illustration, un peu originale, du théorème de Varignon sur deux carrés.
Variantes de la représentation : on notera que, parfois, pour les droites représentées par des cercles, au prétexte de la lisibilité, on fait le choix de les représenter par des arcs de cercle définis par les trois points de la droite.
C’est assez naturel, il s’agit juste d’un choix cohérent de représentation. Par extension, pour une plus grande clarté visuelle , plus que par attachement à la notion orientée des segments (milieu à l’intérieur), parfois on étend ce choix aux segments comme ci-dessus.
Les deux modèles vus pour Pappus seront étendus, d’un point de vue dynamique, au cas euclidien, dans le prochain item de ce menu avec l’un des triples de Steiner.