Après avoir exploré rapidement quelques triangles orthocentriques, nous avons ensuite cherché à construire des triangles bi-orthocentriques, avec donc une double contrainte. Dans cette page, on se propose d’adapter la technique développée pour la recherche de la double orthocentricité à une autre double contrainte, peut-être encore plus originale, que permet ce modèle de Hilbert de la géométrie non arguésienne : l’obtention simultanée d’un orthocentre et de deux hauteurs parallèles !
Présentation des résultats
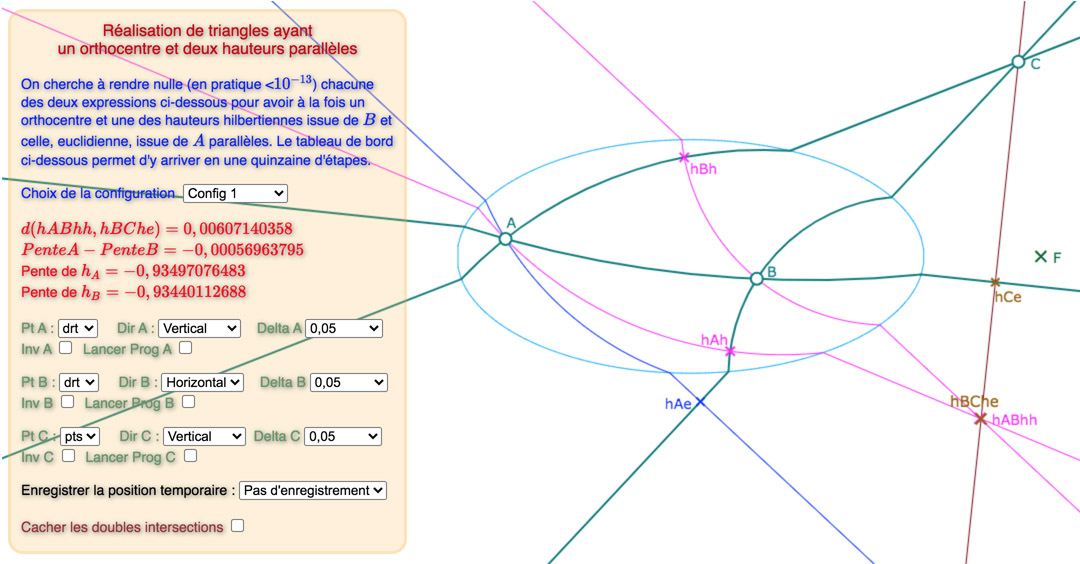
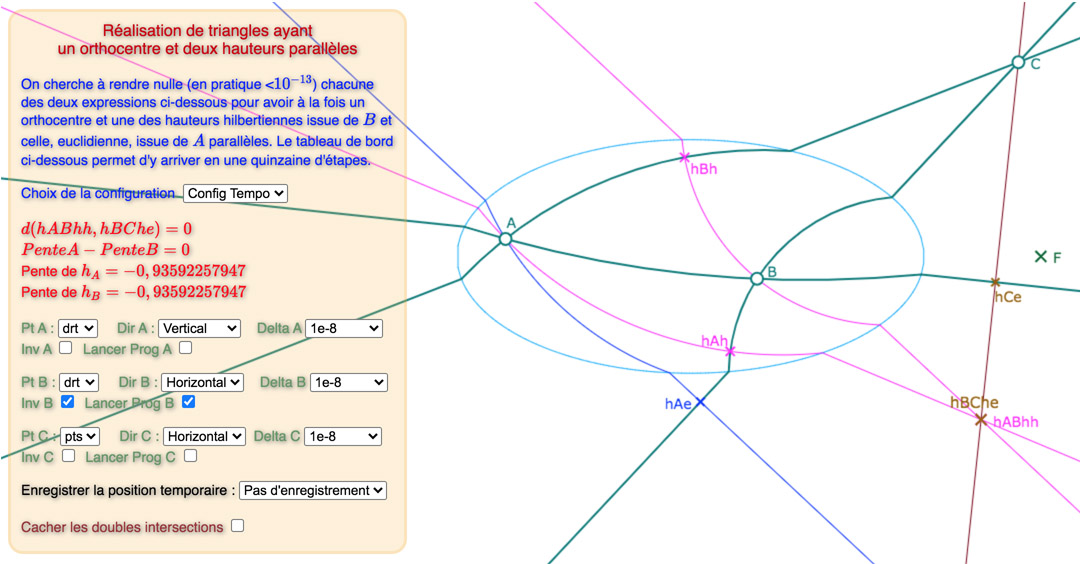
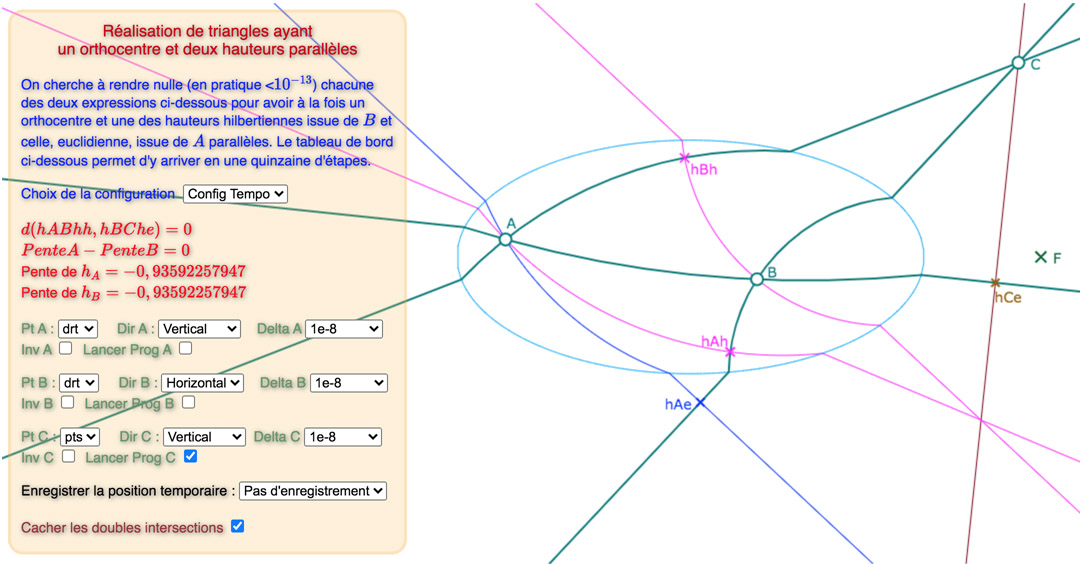
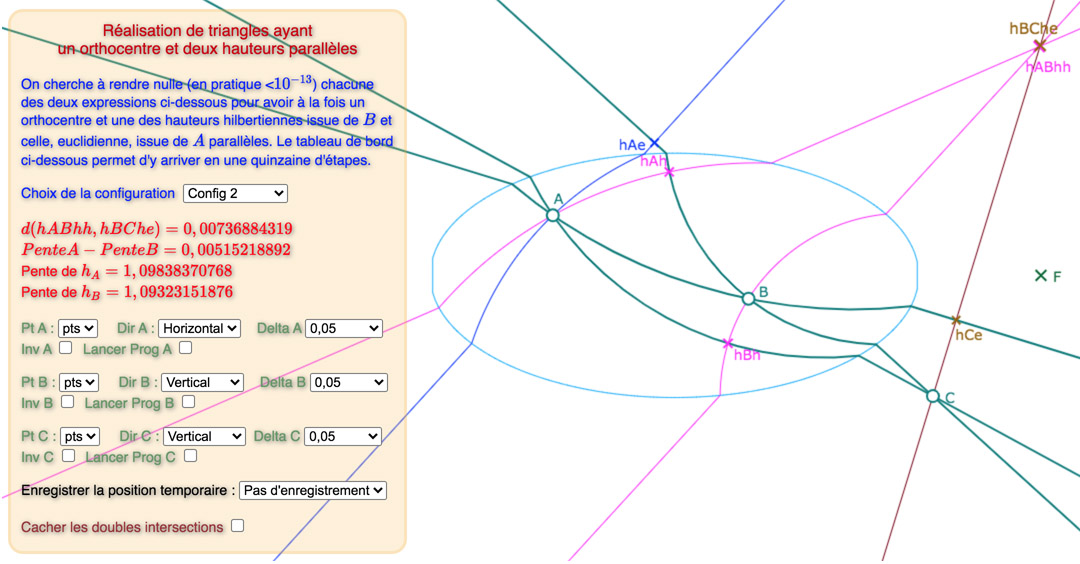
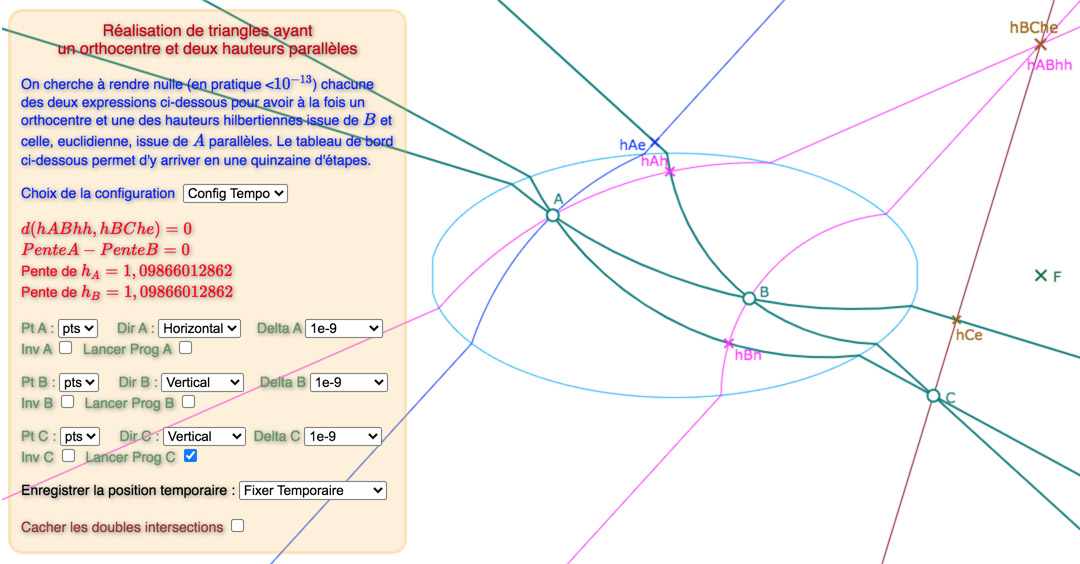
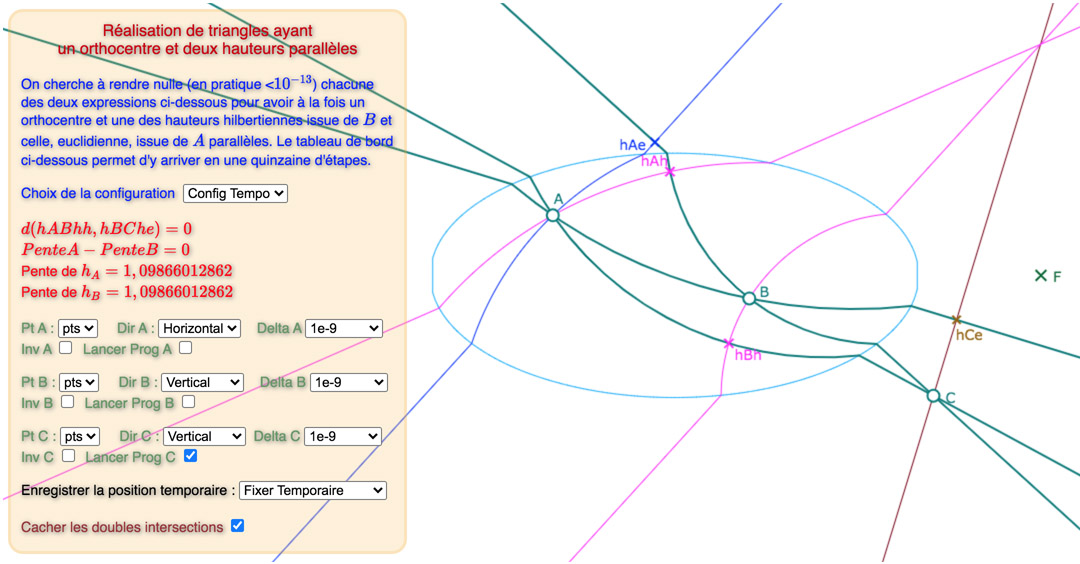
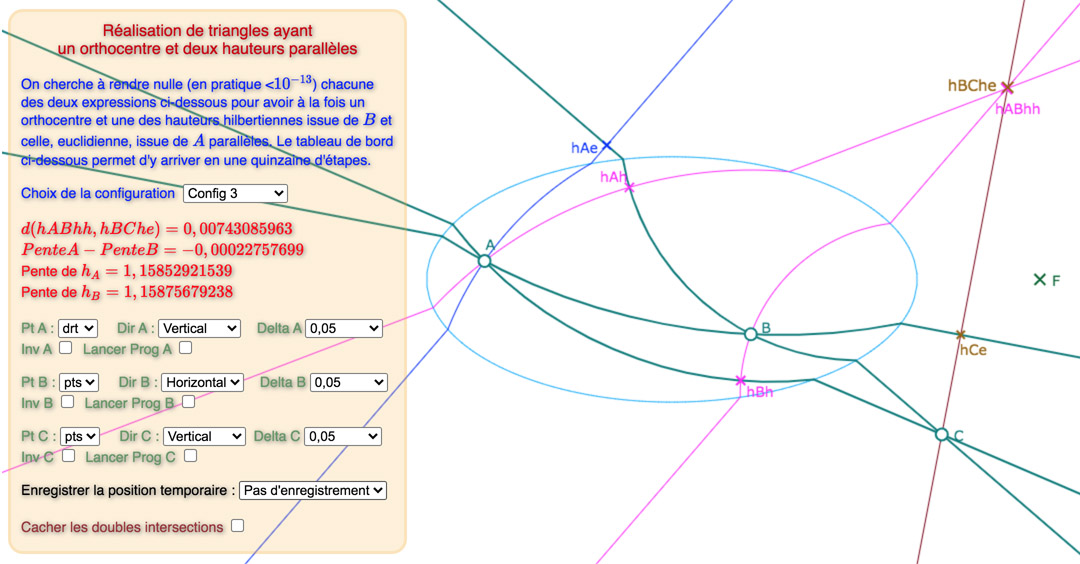
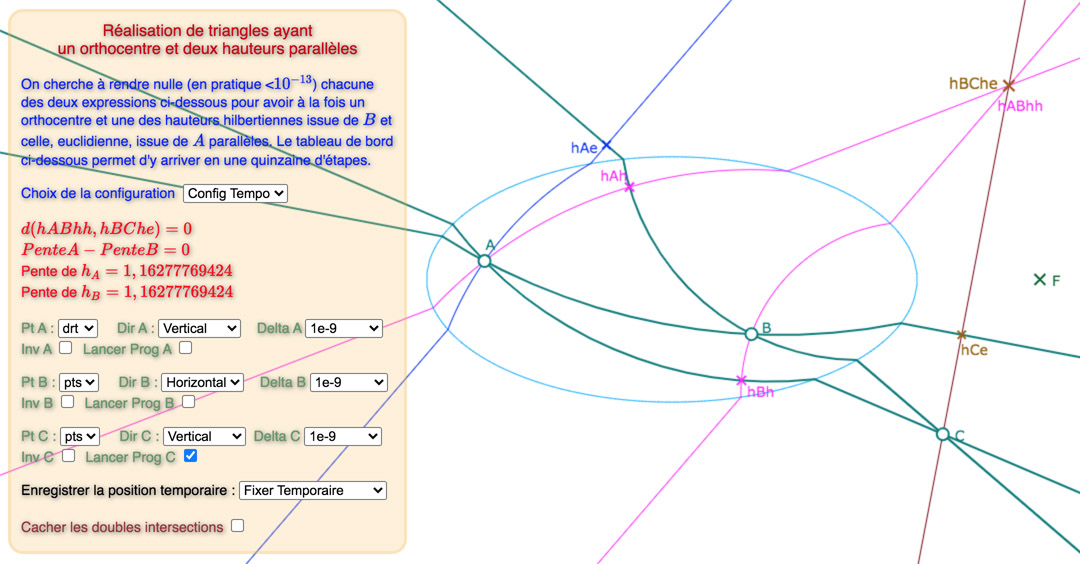
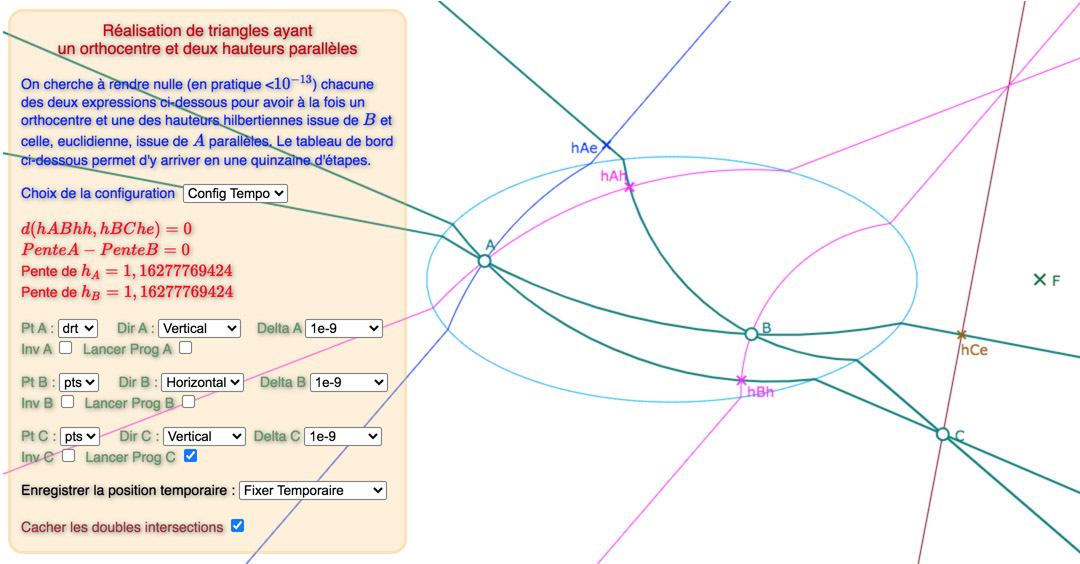
Voici, une galerie de 3 configurations, sur la base du « tableau de bord » déjà utilisée dans la page précédente : tout d’abord une situation de départ choisie proche d’une solution, puis une solution avec les points des intersections des hauteurs, puis une autre avec ces deux points cachés.
La première configuration est construite autour d’hauteurs parallèles de pente négative, les deux autres, de pente positive.
Prendre le temps de percevoir la différence entre les deux premières illustrations (on peut voir \(hBh\) bouger)
La différence, entre les deux premières illustrations, pour les deux autres configurations est plus claire.
Les configurations 2 et 3
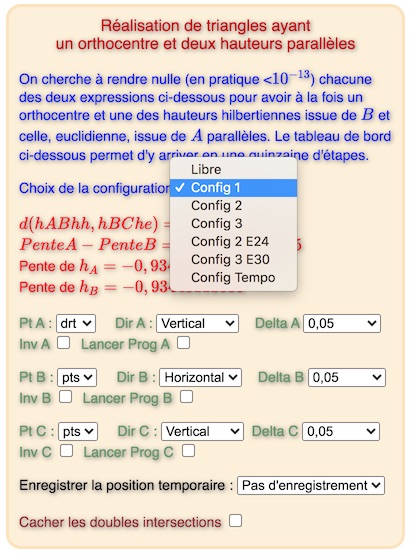
Le commentaire intégré à la figure est assez optimiste en annonçant « une quinzaine d’étapes ». Si pour c’est vrai pour la configuration 1, ce n’est – semble-t-il – plus le cas des deux autres configurations. C’est la raison pour laquelle on propose pour les configurations 2 et 3 la situation de départ et une situation bien plus avancée vers la solution, comme indiqué dans le pop-up des configurations :
Ces deux étapes avancées E24 et E30 ont les distances et pentes suivantes

On peut s’amuser à essayer d’aller au delà pour obtenir la distance et la différence des pentes toutes les deux nulles (environ 6 étapes dans les deux cas) comme dans la galerie précédente mais rien ne bougera à l’écran car modifier des points d’une amplitude maximale de l’ordre du milliardième de l’unité revient à les déplacer de moins d’un millionième de pixel … On peut aussi concevoir que, graphiquement, déjà dans ces étapes, on est sur les solutions.
Ouvrir la figure correspondante dans un nouvel onglet.
Sur la sensibilité de cette figure
La modification du programme, présentée plus loin, est peut-être à l’origine d’une certaine sensibilité de la figure : quand on clique « Fixer Temporaire » cela peut parfois, à la marge certes, mais justement à partir des étapes avancées proposées, modifier les affichages (typiquement \(10^{-11}\) peut devenir \(0\) ).
Rappel de l’utilisation (détaillé à la page précédente) : toujours utiliser « Fixer Temporaire » pour évoluer d’une étape à l’autre (et se mettre dès la première étape en « Config Temporaire ») et revenir à « Pas d’enregistrement » avant de faire de nouvelles modifications.
La configuration 1
Sa résolution – sur la même figure que ci-dessus – est plus simple. Voici une chemin possible
La configuration 1 en 13 étapes. On remarquera qu’il suffit d’aller à jusqu’à \(10^{-8}\) dans l’amplitude.
Remarque : pour la dernière étape, le réglage \(drt\) sur le même sommet convient aussi.

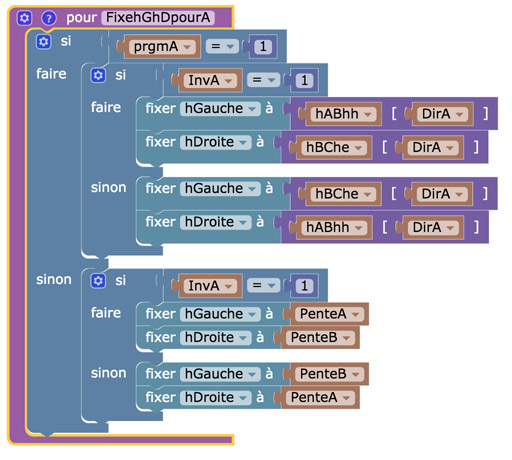
La modification du programme
Les pentes étant des nombres, et non pas des points comme dans la double contrainte pour les triangles bi-orthocentriques, il suffit de faire cette simple modification et adapter les autres procédures.
Complément
Depuis, on est allé plus loin, et plus simplement – en conservant l’aspect dynamique pour le cas traité ici.
Consulter cet article sur la bi-orthocentricité avec hauteurs parallèles.