Milieux de deux points
Pour construire le milieu de deux points dans un modèle quelconque de géométrie non euclidienne, du moins de manière géométrique, c’est-à-dire quand ce n’est pas avec le calcul dans le modèle (menu PS), ou par conjugaison (menu PSH), la procédure classique consiste à construire d’abord le symétrique par rapport à une droite, puis en déduire la construction d’un cercle, et enfin, quand le cercle est facile à construire, il en résulte la construction de la médiatrice par intersection de deux cercles et donc le milieu.
On pourrait faire cela aussi dans le cas de ce modèle. Mais ce serait assez long en terme d’objets intermédiaires. Compte tenu du contexte bien spécifique de la géométrie elliptique et du modèle conforme que l’on utilise, on peut faire ceci : étant donnés deux points \(A\) et \(B\), et \(P\) le pôle de \((AB)\). Alors \(APB\) étant isocèle, sa bissectrice en \(P\) est aussi médiatrice de \(A\) et \(B\). Or, le modèle étant conforme, la bissectrice se construit facilement à partir de la bissectrice intérieure des tangentes euclidiennes aux droites elliptiques \((AP)\) et \((BP)\). On a donc à la fois la médiatrice et le milieu des deux points.
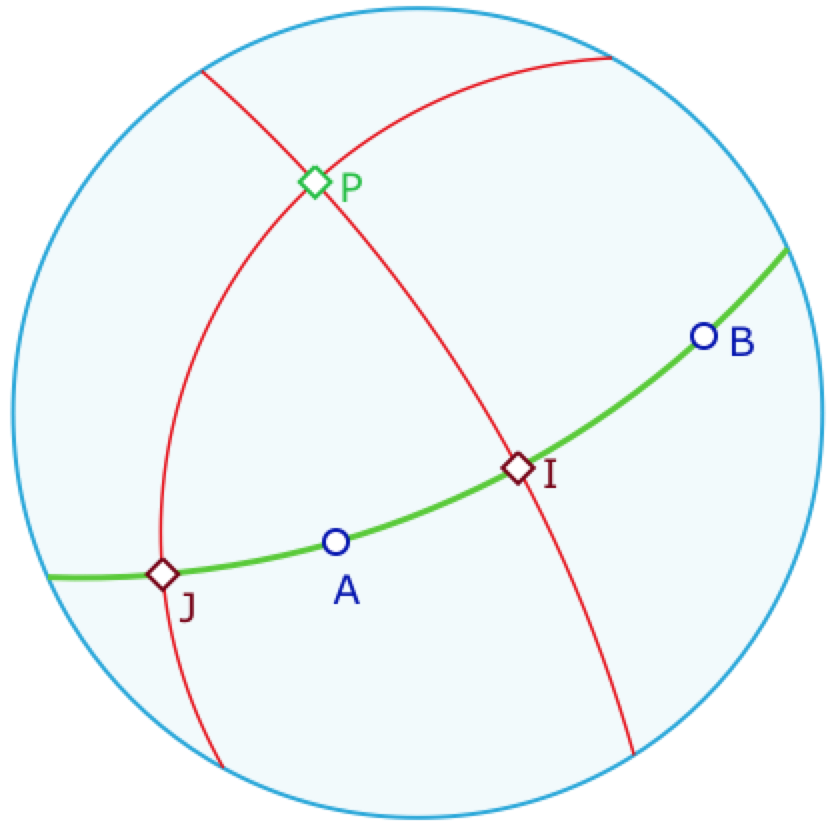
La médiatrice et le milieu ? Pas vraiment.
En effet, si on note \(d=(PI)\) la médiatrice obtenue, par construction, avec la bissectrice de l’angle en \(P\) du « triangle sphérique » \(APB\) (soit le triangle formé des « segments intérieurs »). Alors la droite \(d’\) perpendiculaire en \(P\) à \(d\) coupe elle aussi \((AB)\) en un point \(J\), et \(d’=(PJ)\) est aussi perpendiculaire à \((AB)\). Et par les propriétés algébriques des isométries, comme vues dans le cas hyperbolique, on peut écrire \(s_{d’} o s_d=s_P\) et que \(s_P(A)=A\). Il en résulte que \(s_{d’}(B)=A\), autrement dit \((PJ)\) est un autre axe de symétrie de \((A\) et \(B\).
On appelle médiateur de deux points \(A\) et \(B\) la réunion des deux médiatrices, axes de symétrie qui échangent \(A\) et \(B\), et milieux les deux points les intersections de \((AB)\) avec chacune de ces deux droites. Deux points ont donc deux milieux.
Par construction chaque médiatrice est la polaire du milieu qu’elle ne contient pas. Le triangle IPJ est tripolaire.
Figure d’exploration sur les milieux, médiatrices, médianes (droites) d’un triangle \(ABC\) (droites)
Comme les objets sont tous créés en même temps, la macro Méd et milieux crée à la fois le pôle, le médiateur et les deux milieux de deux points.
Déjà appliquée à \(A\) et \(B\), le faire sur \(B\) et \(C\), puis sur \(C\) et \(A\). On peut explorer les différents éventuels alignements ou points de concours.
La même figure, terminée, avec de nombreux paramétrages d’affichage, est disponible un peu plus loin, pour d’autres explorations.
Les centres des cercles circonscrits
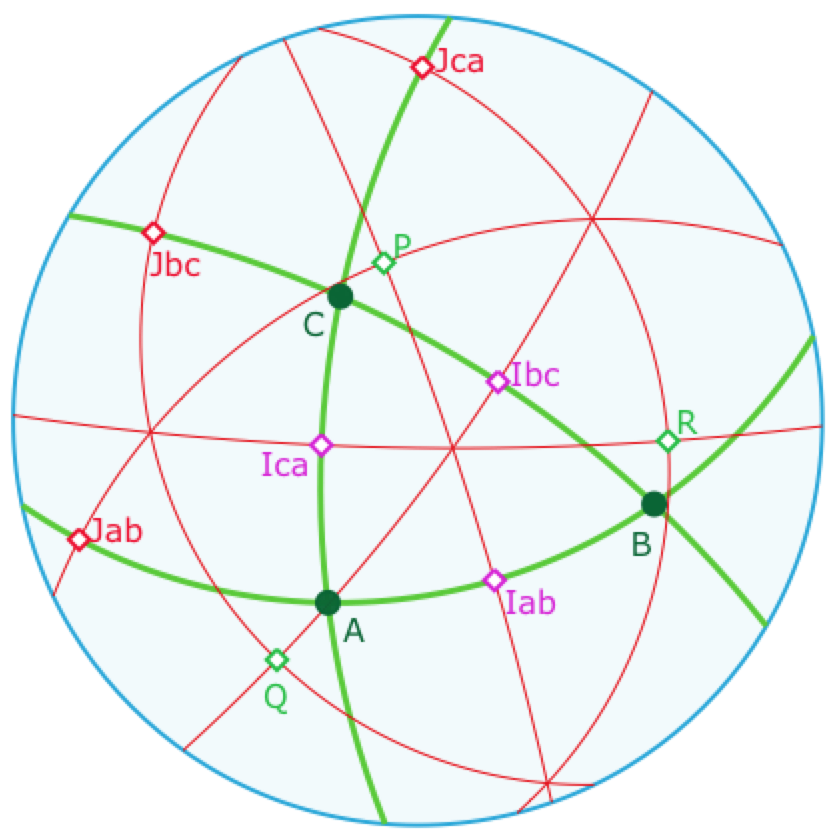
Tout d’abord les six médiatrices sont concourantes trois à trois. Dans le cadre de l’axiomatique de Bachmann, on sait que les médiatrices sont en pinceau, et donc, ici, concourantes. Cela signifie que le triangle \(ABC\) a quatre cercles circonscrits, un dans chacune des 4 composantes connexes construites par le triangle.
Les droites des milieux
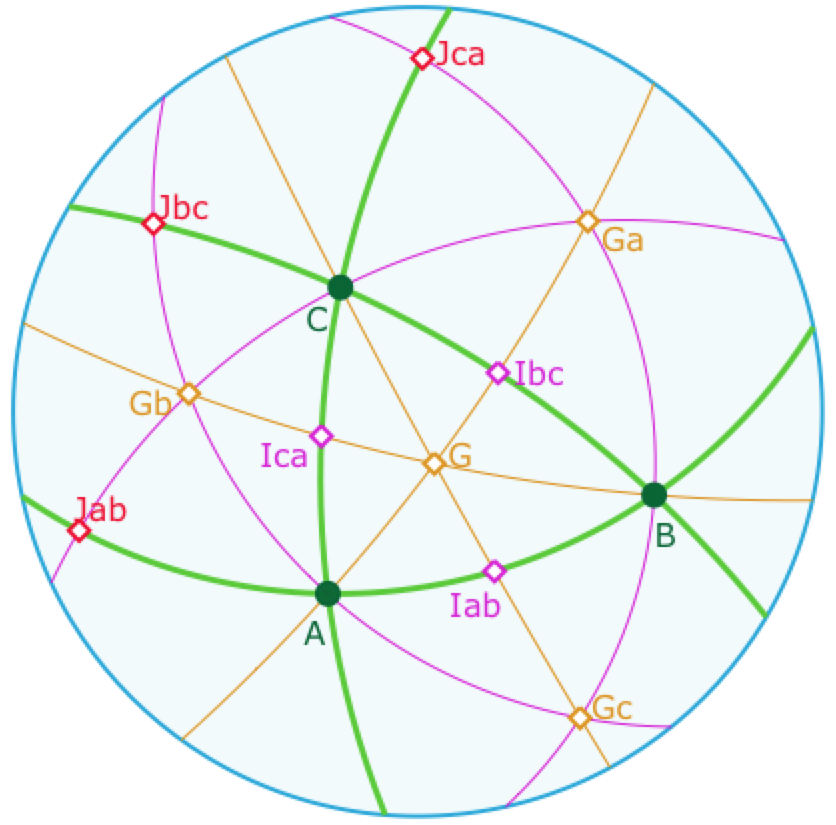
En notant \(I_{xy}\) les milieux des segments «sphériques», c’est-à-dire « intérieurs » pour le modèle – obtenus par les bissectrices intérieures issues du pôle de la droite, et \(J_{xy}\) les milieux des compléments , avec des notations propres au modèle, au sens où, si ils sont tous les deux les milieux de deux sommets, mais pas nécessairement les milieux des segments du triangle elliptique.
On obtient alors que la droite des milieux intérieurs coupe le troisième côté en son milieu extérieur.
Les trois points \(J_{xy}\) sont eux aussi alignés.
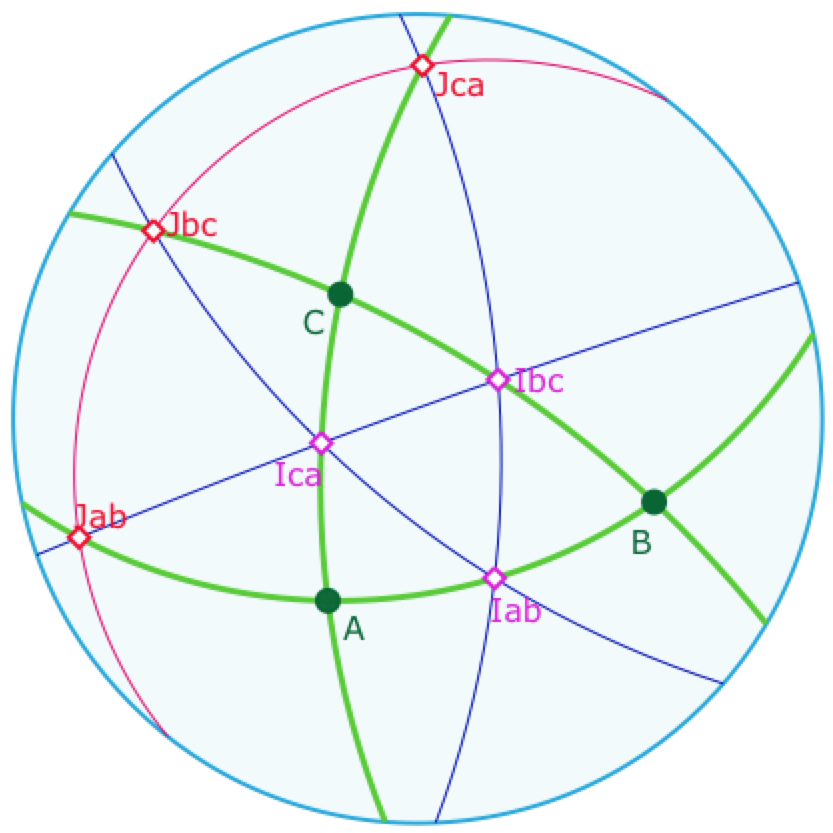
Le théorème absolu de la droite des milieux – montré dans le cas hyperbolique mais dont les arguments utilisés sont absolus, assure que la médiatrice du troisième « côté » est perpendiculaire commune aux deux droites.
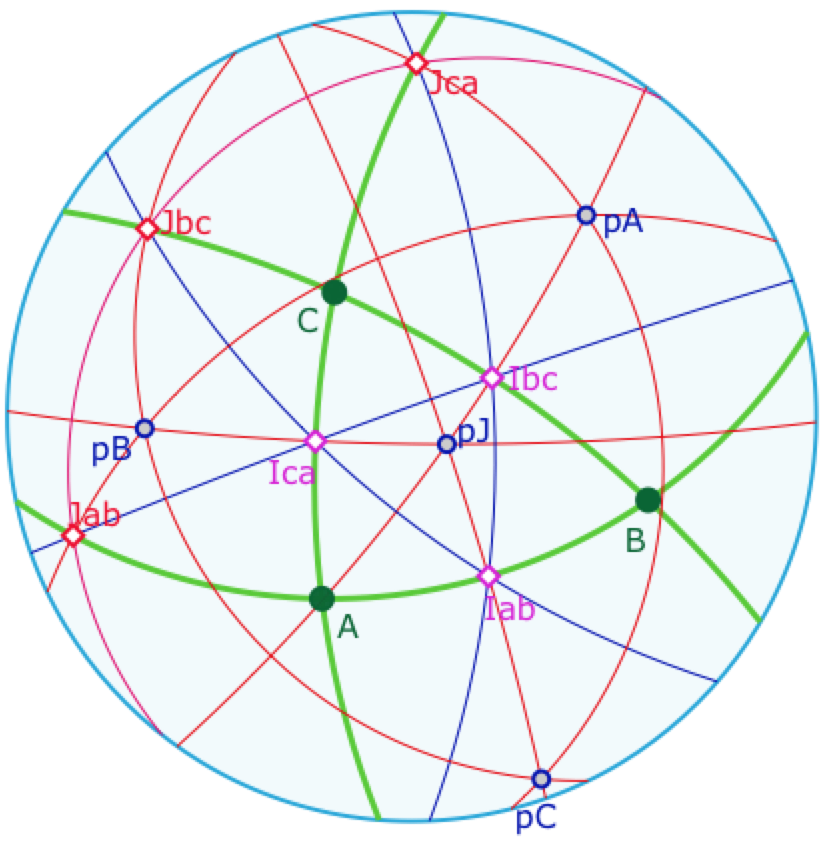
Il est facile d’en conclure que les intersections des médiatrices – les centres des cercles circonscrits – sont les pôles des droites des milieux. Par exemple l’intersection \(pJ\) est le pôle de la droite des milieux \(J_{xy}\).
Les médianes
Que les médianes soient en pinceau est un résultat général non trivial, même dans le cas elliptique. Il nécessite des outils techniques présentés ici. Bien entendu cela pourrait se montrer plus facilement «dans un modèle» avec les propriétés géométriques du modèle, mais cela ne prouve pas que la propriété est elliptique.
Comme pour les centres des cercles circonscrits, il y a quatre intersections des médianes. Le triangle \(G_aG_bG_c\) n’a pas de propriétés générales particulières par rapport au triangle \(ABC\).
ne pas hésiter à relancer son chargement
Vous pouvez faire apparaître les point souhaités avec les cases à cocher. Par ailleurs la macro « cercle elliptique » est disponible, vous pouvez tracer les 4 cercles circonscrits. Ils ont pour centres les pôles des droites des milieux (\(P_x\)). Vous pouvez aussi explorer la partie proposée ci-après sur les polaires des points \(G_x\). On peut prendre les pôles des droites \((G_xG_y)\), les constructions sont un peu plus courtes.
Exemple d’une autre exploration possible
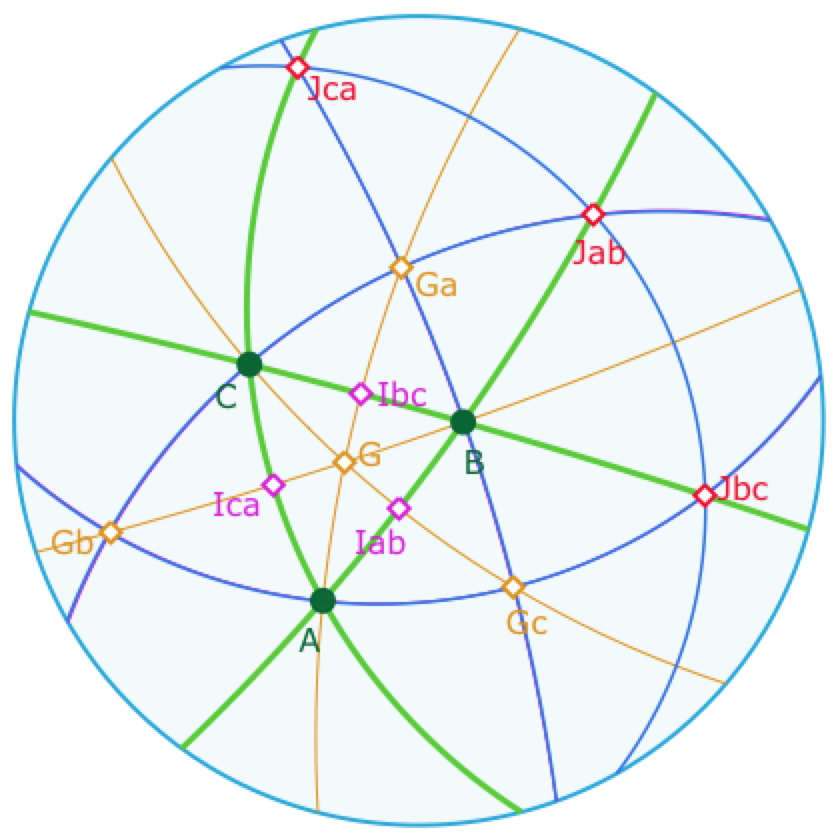
Ci-dessous on a construit, en bleu, les polaires ces 4 centres \(G, G_a, G_b, G_c\). La configuration est telle que le triangle \(G_aG_bG_c\) est tripolaire. Il est assez immédiat de voir que nécessairement, dans ce cas, le triangle initial \(ABC\) est équilatéral. Par exemple on peut voir que les médiatrices « intérieures » coïncident avec les médianes « intérieures. Il en résulte que les côtés du triangle sont les droites des milieux de \(G_aG_bG_c\). On a donc cette configuration particulière où les triangles \(ABC\) et \(G_aG_bG_c\) ont les même milieux « extérieurs » \(J_{xy}\). Et dans ce cas, la polaire de \(G\) est la droite de ces milieux extérieurs car \(G\) n’est autre que le point \(pJ\) des illustrations de la page précédente.
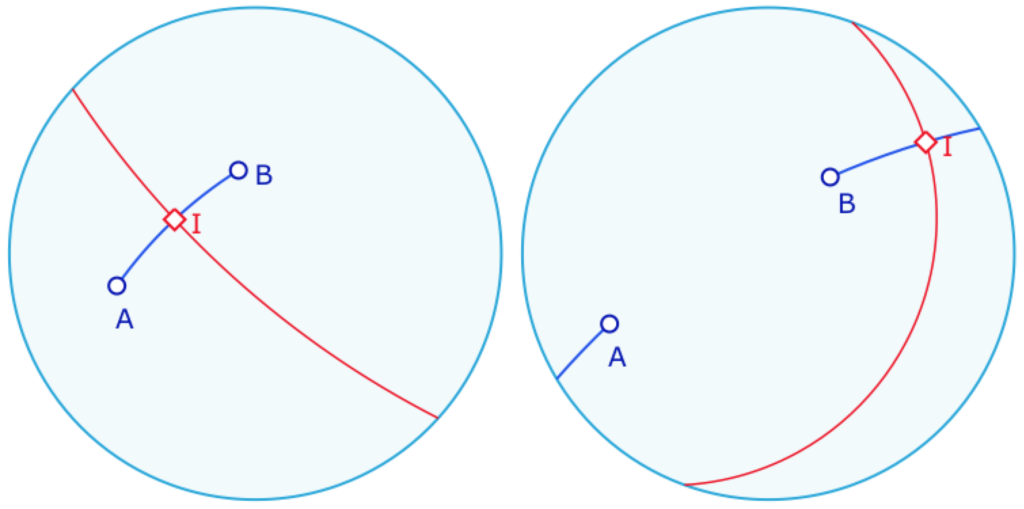
Milieu d’un segment – Droites remarquables intrinsèques
Si on ne s’intéresse plus aux couples de points, mais aux segments alors un segment elliptique, en tant que tel, n’a qu’un seul milieu, et une seule médiatrice.
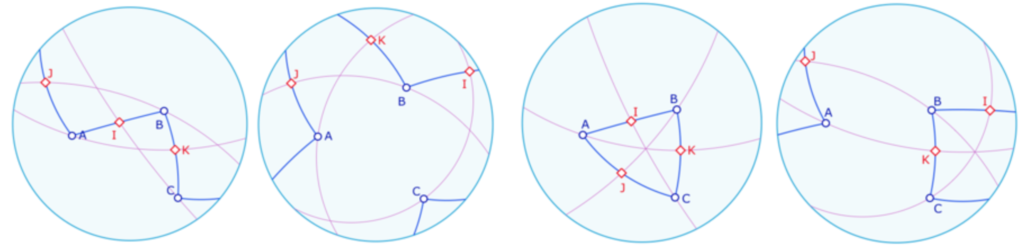
Cela éclaire d’un regard nouveau le « type elliptique » des triangles de cette géométrie : on voit ci-dessous que le triangle «de type elliptique » – les deux illustrations de gauche – a les médiatrices (uniques) de ses côtés elliptiques non concourantes, alors que le cas dit « de type euclidien » – les deux illustrations de droite – ont leurs médiatrices concourantes : il y a donc un cercle circonscrit dont le centre est l’intersection des médiatrices intrinsèques au triangle.
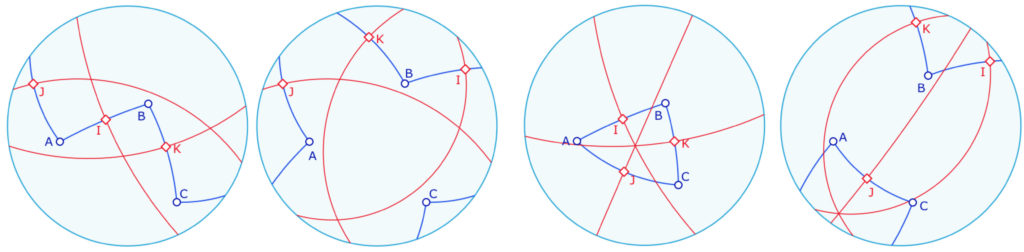
Bien entendu les trois intersections deux à deux de ces médiatrices sont aussi centres des autres cercles circonscrits des trois points \(A, B\), et \(C\).
Les médianes intrinsèques d’un triangle considéré comme réunion de trois segments
La situation est la même que pour les médiatrices : les médianes intrinsèques sont concourantes pour les triangles «de type euclidien» et ne le sont pas pour les triangle «de type elliptique».
En géométrie, le mot triangle signifie souvent un triplet de trois points (géométrie affine par exemple, avec les barycentres). en géométrie euclidienne on identifie souvent le triplet au triplet de trois segments car il n’y a aucune ambiguïté. Il n’y en n’a pas non plus dans le cas hyperbolique. Le problème ne se rencontre que dans le cas elliptique car, comme les droites sont bornées, le complément d’un chemin – sur une droite – allant de \(A\) à \(B\) est aussi borné, et donc a un milieu et une médiatrice.
Le terme trilatère, utilisé en géométrie hyperboliques pour parler de trois droites non en pinceaux mais non nécessairement sécantes est utilisable aussi pour parler des trois droites \((AB), (BC), (CA)\) d’un triangle \(ABC\), mais ne suffit pas pour le cas elliptique car on veut différencier la situation avec les segments. En fait, la différence importante est entre la géométrie elliptique et la géométrie sphérique dans laquelle, pour des raisons par exemple de trajets en mer, les triangles peuvent être tracés avec des côtés dont la longueur n’est pas nécessaire la distance entre les sommets..
La différence – et la nouveauté elliptique – est dans la spécificité de ce que l’on appellera désormais un triangle elliptique (ou intrinsèque), considéré comme la réunion des trois segments elliptiques \([AB], [BC], [CA]\), dont la longueur est la distance entre les sommets, avec ses milieux, médianes et médiatrices intrinsèques. On conservera le terme triangle sphérique quand la longueur des côtés peut ne pas être une distance.
Manipulations dynamiques sur les triangles, milieux, médiatrices et médianes intrinsèques
Relation entre type «elliptique» ou «euclidien» des triangles et les points de concours des droites intrinsèques
Cette figure peut être longue à charger, ne pas hésiter à relancer son chargement par la première icone.