Le thème de l’orthogonalité, comme dans le cas du modèle de Hilbert, va être très riche. Mais à la différence du précédent modèle, il va être beaucoup plus facile non seulement à étudier, mais surtout à mettre en œuvre. Nous pourrons donc aller beaucoup plus loin en terme de figures dynamiques.
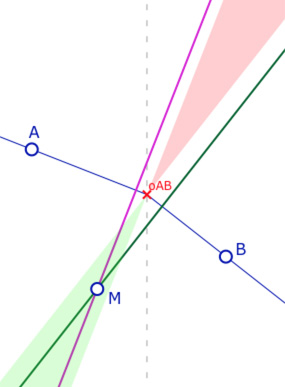
Commençons par les droites de Moulton dites à pente négative. Comme on l’a vu dans la page sur les angles, l’angle en \(o_{AB}\) est un angle plat. Alors, une bonne représentation mentale de la situation est de se dire que le demi-plan inférieur se comporte comme s’il était replié sur lui-même, invitant à des perspectives nouvelles dans cette partie de repli, alors que le demi-plan supérieur se comporte comme s’il était déchiré – dans la même proportion – laissant une partie sans perpendiculaire possible à la droite \((AB)\). Voyons une première illustration.
Les perpendiculaires euclidiennes aux deux demi-droites de la M-droite \((AB)\) en \(o_{AB}\) délimitent deux régions : en dessous, issue du point \(o_{AB}\), une partie verte dans laquelle on peut mener deux perpendiculaires à la droite \((AB)\) et, au-dessus de la droite, une partie rouge dans laquelle aucune perpendiculaire à \((AB)\) ne peut être menée. En dehors de ces deux parties, par un point il passe une et une seule perpendiculaire à \((AB)\) .
Voyons maintenant ce qu’il en est de l’orthogonalité pour les M-droites à pente positive, qui sont les droites euclidiennes usuelles.
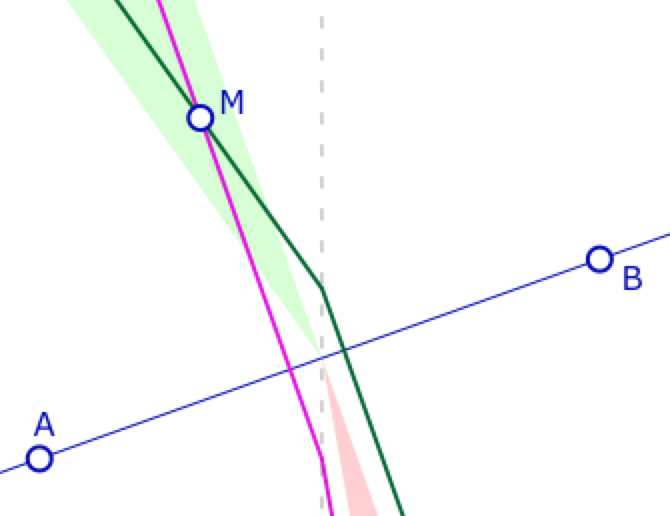
Il existe aussi une partie verte, toujours issue du point d’origine \(o_{AB}\), cette fois-ci au dessus de la droite, depuis laquelle on peut mener deux perpendiculaires à la droite \((AB)\), et une partie rouge, en dessous, de laquelle on ne peux pas mener de perpendiculaire à la droite \((AB)\).
Dans cette situation où pente de (AB) est positive, les régions vertes et rouges ne sont pas symétriques.
En effet, la perpendiculaire euclidienne à \((AB)\) en \(o_{AB}\) étant à pente négative, elle permet la construction de deux droites de Moulton différentes pour lesquelles chacune des demi-droite de cette perpendiculaire euclidienne est une partie de la droite de Moulton : comme la pente est double pour la partie à abscisse positive, cela donne cette dissymétrie que l’on peut voir ci-contre.
En dehors de ces deux parties, par un point du plan il passe une et une seule perpendiculaire à la droite \((AB)\) comme illustré ci-dessous.
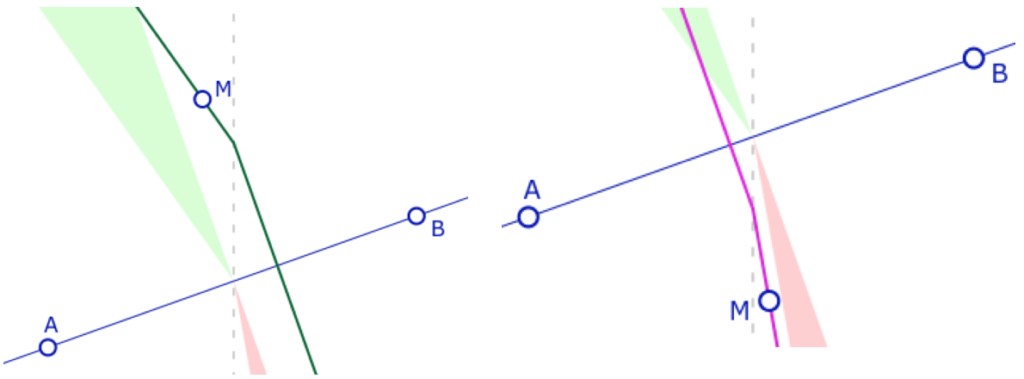
Dans la suite, on notera \(psp_{AB}\) la partie sans perpendiculaire autour de la droite \((AB)\), la partie rose dans les illustrations précédentes. \(psp_{AB}\) est au dessus de la droite quand elle est à pente négative et en dessous quand elle est à pente positive. Ses points sont à abscisse positive.
De même on notera \(pdp_{AB}\) la partie ayant deux perpendiculaires autour de la droite \((AB)\), la partie verte dans les illustrations précédentes. \(pdp_{AB}\) est en dessous de la droite quand elle est à pente négative et au dessus quand elle est à pente positive.Ses points sont à abscisse négative.
Premier contact dynamique avec la M-orthogonalité
On peut agir sur les trois points \(A\), \(B\) et \(M\). Penser à rendre la pente de \((AB)\) positive.
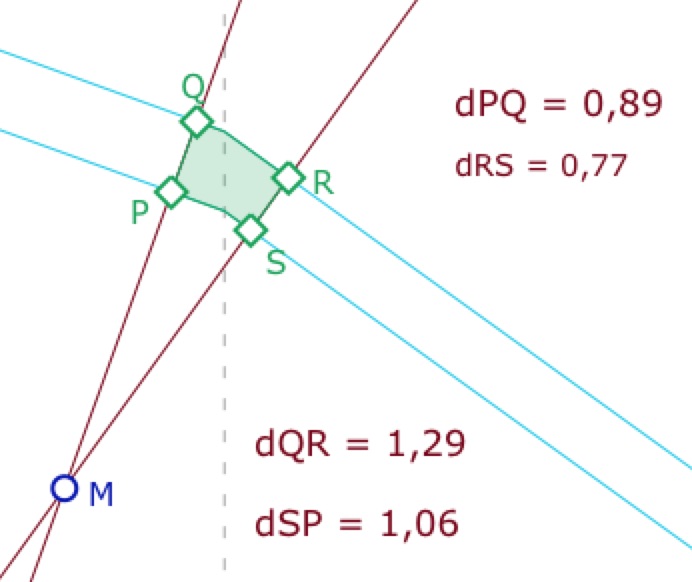
Première application : rectangle de Moulton
En prenant une parallèle à une droite donnée, on peut facilement construire un quadrilatère avec quatre angles droits. C’est donc un rectangle, avec deux côtés parallèles. On remarque que les côtés opposés ne sont de même longueur.
Hauteurs d’un triangle
Un triangle peut avoir de 1 à 5 hauteurs : il suffit, pour s’en rendre compte, de placer, sur la figure dynamique suivante,
a. Pour une seule hauteur : deux sommets dans les zones \(psp_{XY}\) de deux côtés, ci-dessous \(psp_{AB}\) et \(psp_{AC}\)
b. Pour cinq hauteurs : deux sommets dans les zones vertes de deux côtés, ci-dessous \(pdp_{AC}\) et \(pdp_{BC}\). Toutes les configurations intermédiaires sont possibles.
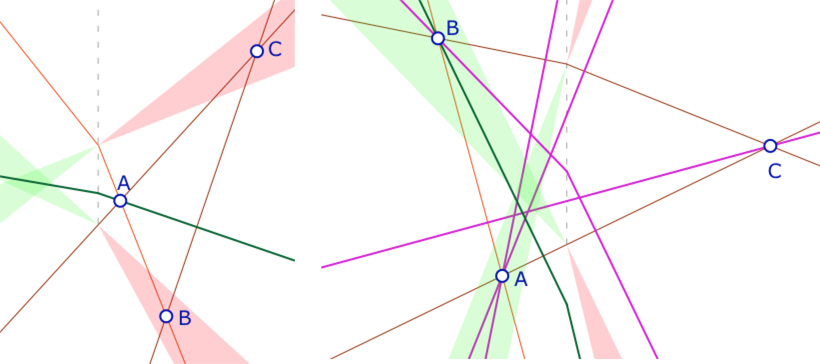
Hauteurs d’un triangle – Recherche d’une situation orthocentrique simple.
Exploration : il existe une configuration géométrique élémentaire, très simple, générique, qui assure qu’un type de triangle de Moulton – bien entendu non euclidien – est orthocentrique. Le lecteur est invité, par manipulation à chercher cette première situation générique. Puis ensuite chercher pourquoi et rédiger votre premier théorème non-arguésien.
Triangles orthocentriques géométriques
On nommera ainsi les M-triangles dont l’orthocentre existe par un argument géométrique élémentaire basé sur une dilatation de rapport 1/2 ou 2 :
Lemme : soient trois droites euclidiennes à pentes négatives. Alors ces droites sont concourantes si et seulement si les droites de Moulton associées le sont.
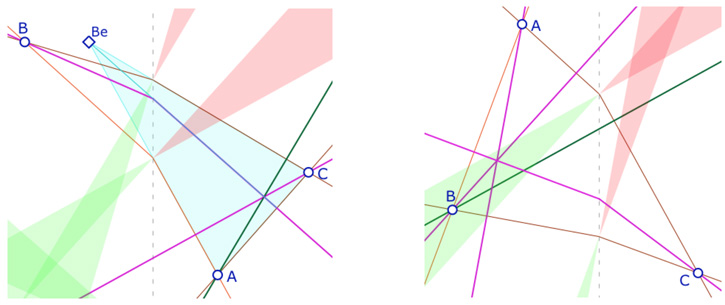
Ci-contrre, à gauche, l’orthocentre du M-triangle \(ABC\) existe car c’est aussi l’orthocentre du triangle euclidien \(AB_eC\), avec \(B_e \left( \frac{x(B)}{2}, y(B) \right)\). De même dans l’illustration de droite. Dans les deux cas, on a deux droites de Moulton passant par un sommet et la hauteur issue de ce sommet qui sont à pentes négatives, donc le lemme précédent peut s’appliquer, à condition que les pieds des trois hauteurs soient dans le même demi plan par rapport à l’axe des ordonnées.
Un autre contexte dans lequel on peut appliquer le lemme est le cas où ce sont les trois hauteurs qui sont à pentes négatives – et donc les côtés du triangle à pentes positives – comme dans les deux illustrations ci-dessous.
Remarque : le lemme n’est applicable que si les sommets du triangle et les trois pieds des hauteurs sont tous les six dans le même demi-plan par rapport à l’axe des ordonnées.
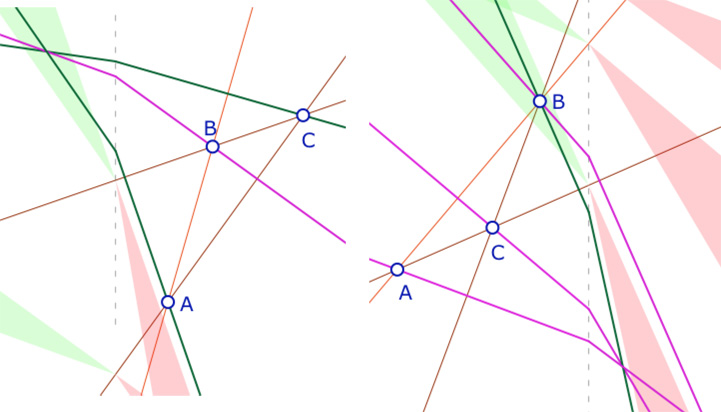
à gauche : le triangle est dans le demi plan à abscisses positives et l’orthocentre est à abscisse négative.
à droite : c’est l’inverse, les sommets du triangle sont à abscisses négatives et l’orthocentre est à abscisse positive.
Dans les deux cas, les six points, sommets et pieds des hauteurs sont dans le même demi-plan.
Chacun peut reproduire, dans la figure précédente, ces différents résultats, et explorer plus avant quelques variantes.
En manipulant la figure dynamique précédente, on peut observer, empiriquement, l’existence d’orthocentres en dehors de ces cas géométriques. On remarquera que ce sont, souvent, des cas bien particuliers. Nous allons ainsi consacrer deux pages de ce menu sur ces différents orthocentres que l’on nommera algébriques.
Avant cela, la section suivante se propose de prouver qu’un M-triangle a toujours au moins une hauteur et au plus cinq hauteurs.
Nombre de hauteurs d’un triangle
Un triangle a toujours au moins une hauteur
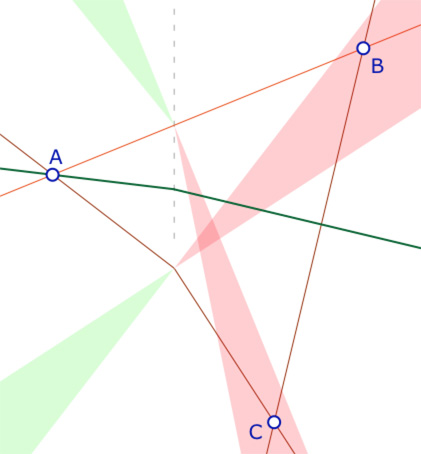
On se place dans le cas où il ne peut y avoir au plus qu’une seule perpendiculaire : deux sommets (disons \(B\) et \(C\)), sont dans les parties sans perpendiculaire des côtés opposés, \(psp_{AC}\) et \(psp_{AB}\) respectivement. D’après ce qui a été dit, ces deux sommets sont donc à abscisse positive. Il s’agit de montrer que le troisième sommet, \(A\), n’est jamais dans la partie \(psp_{BC}\).
L’illustration ci contre est un cas évident car \(A\) est à abscisse négative. Le problème ne se pose que si \(A\) est aussi à abscisse positive. C’est ce que l’on suppose désormais.
Nous allons alors montrer que nécessairement l’une des deux droites \((AB)\) ou \((AC)\) est à pente positive et l’autre à pente négative. L’existence de la hauteur issue de \(A\) en découlera.
Dans la suite on notera \(y_{MN}(0)\) l’ordonnée à l’origine de la droite \((MN)\).
a) Supposons que \((AC)\) soit à pente négative.

Comme \(B \in psp_{AC}\), on a \(y_B > y_{AC}(0)\) et donc \(y_B > y_C\) et \(y_B > y_A\). Ces deux inégalités entrainent que la droite \((AB)\) ne peux pas être à pente négative. En effet, comme \(C \in psp_{AB}\), on aurait \(y_C > y_{AB}(0) > y_B\). Donc \((AB)\) est à pente positive. De \(y_B > y_A\) on en déduit \(x_A < x_B\). Cette pente positive permet d’écrire \(y_C < y_{AB}(0) < y_A\). Deux possibilités :
• Si \((BC)\) est à pente positive (à gauche), les points \(M \in psp_{BC}\) vérifient \(y_M < y_{BC}(0) < y_C\). Or on a \(y_A > y_C\) donc \(A \notin psp_{BC}\), la hauteur existe.
• Si \((BC)\)] est à pente négative (à droite), on a \(y_{BC}(0) > y_B > y_A\) et donc, là encore \(A \notin psp_{BC}\), et la hauteur existe.
b) Supposons que \((AC)\) soit à pente positive. La preuve est symétrique de la précédente (on inverse quasiment \(B\) et \(C\)).
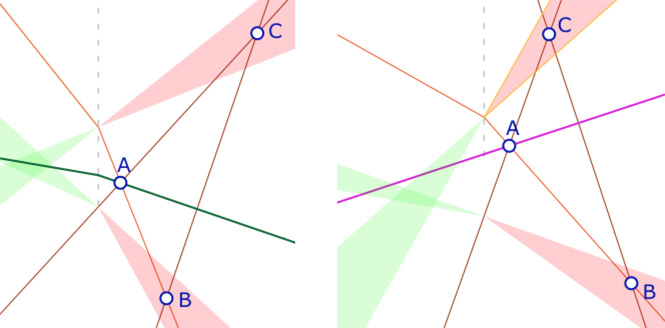
De \(B \in psp_{AC}\), \(y_B < y_{AC}(0)\) et donc \(y_B < y_C\) et \(y_B < y_A\). Ces deux inégalités entrainent que la droite \((AB)\) ne peux pas être à pente positive. En effet, comme \(C \in psp_{AB}\), on aurait \(y_C < y_{AB}(0) < y_B\). Donc \((AB)\) est à pente négative. De \(y_B < y_A\) on en déduit \(x_A < x_B\). A nouveau deux possibilités :
• Si \((BC)\) est à pente positive – à gauche – \(y_{BC}(0) < y_B < y_A\) et donc \(A \notin psp_{BC}\).
• Si \((BC)\) est à pente négative – à droite – \(y_{BC}(0) > y_C > y_A\) et donc \(A \notin psp_{BC}\).
Dans tous les cas, on ne peut avoir les trois sommets du triangle dans la partie sans perpendiculaire des sommets du côté opposé. Ainsi, un triangle de Moulton admettent moins une hauteur.
Un triangle admet au plus cinq perpendiculaires
Là encore, la preuve est très similaire à ce qui précède, un peu comme une preuve duale. On se place donc dans une situation où il y a cinq hauteurs, et nous allons montrer qu’il ne peut y avoir une sixième hauteur.
On se place dans la situation où \(A \in pdp_{BC}\) et \(B \in pdp_{AC}\). On détaille le cas où \(x_C <0\), l’autre cas se traiterait de la même façon.Il s’agit de montrer que \(C \notin pdp_{AB}\).
Compte tenu de la symétrie des situations et des raisonnements, comme vu lors de la preuve « au moins une hauteur », on se limite à étudier le cas où la pente de la droite \((BC)\) est positive.
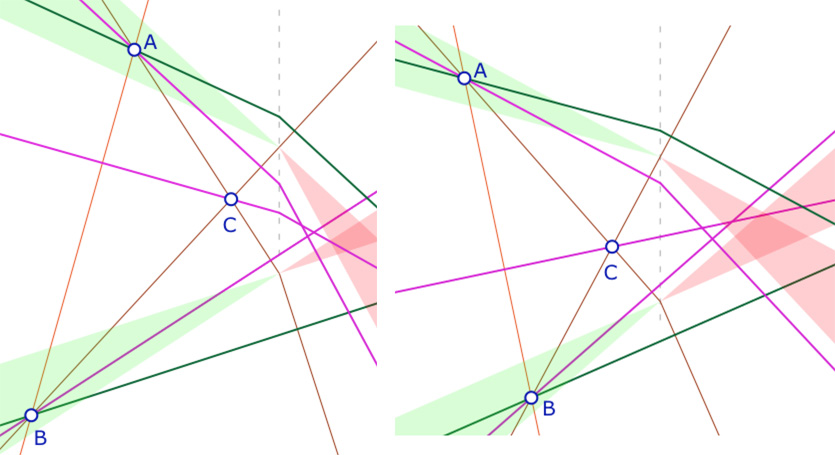
Avec ces hypothèses, on a \(y_A > y_{BC}(0) > y_B\) et \(y_A > y_{BC}(0) > y_C\). Ces inégalités induisent que la droite \((AC)\) est nécessairement à pente négative. En effet, si ce n’était pas le cas, de \(B \in pdp_{AC}\) on tirerait \(y_B > y_{AC}(0) > y_A\) ce qui est impossible. Donc \((AC)\) est à pente négative, et en particulier \(y_B < y_{AC}(0) < y_A\). Il y a alors deux cas :
• Si \((AB)\) est à pente positive – illustration de gauche – \(y_{AB}(0) > y_A > y_C\) et donc \(C \notin pdp_{AB}\).
• Si \((AB)\) est à pente négative – illustration de droite – \(y_{AB}(0) < y_B < y_C\) et donc \(C \notin pdp_{AB}\).
Ainsi, dans tous les cas, il ne peut y avoir de sixième hauteur issue de \(A\).
Complément : présentation (assez technique) de la construction des perpendiculaires.