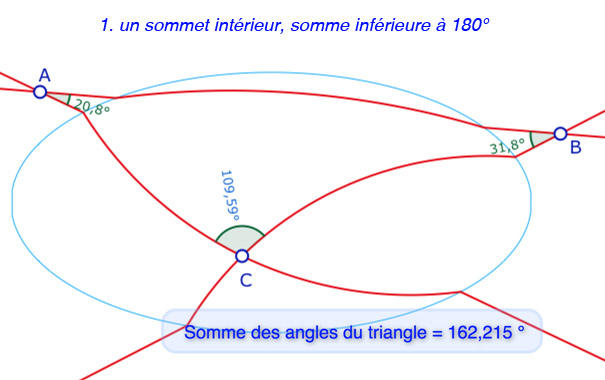
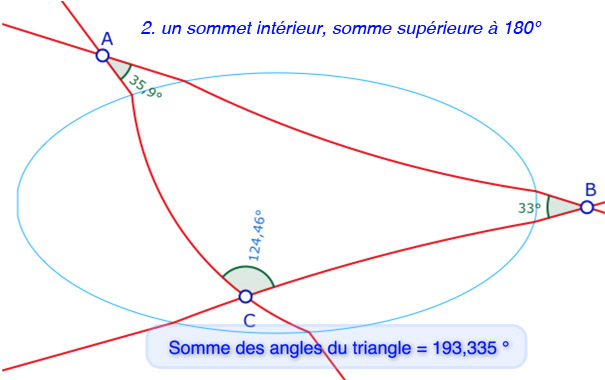
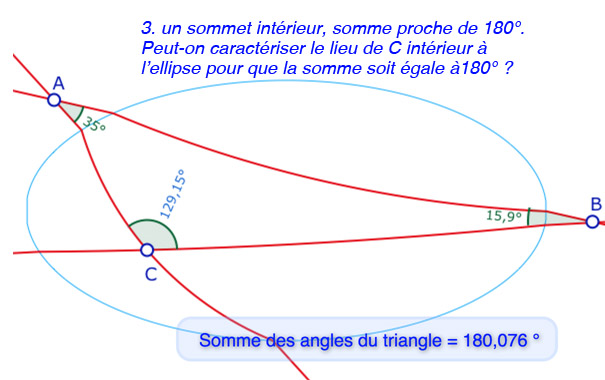
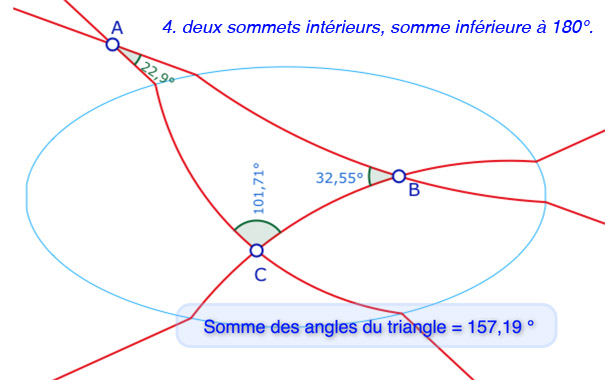
Pour les angles, cette géométrie a des propriétés spécifiques, différentes de la géométrie hyperbolique (la somme des angles d’un triangle est toujours inférieure à un plat) ou elliptique (cette somme est alors toujours supérieure à un plat). Ici on peut avoir les deux possibilités. La question des valeurs extrémales pour la somme des angles est encore à étudier. Bien entendu si les trois sommets sont intérieurs ou tous trois extérieurs à l’ellipse, la somme des angles est égale à un plat. On s’intéresse donc aux autres cas. Voici une galerie de six exemples de possibilités.
On remarquera que pour un sommet intérieur à l’ellipse, il y a une marque d’une couleur qui colle aux arcs du sommet, et une mesure d’une autre couleur, car la mesure n’est bien entendu pas celle de la marque visuelle (pour les angles intérieurs à l’ellipse). La construction des deux marques n’est pas toujours stable.
Figure générique d’exploration
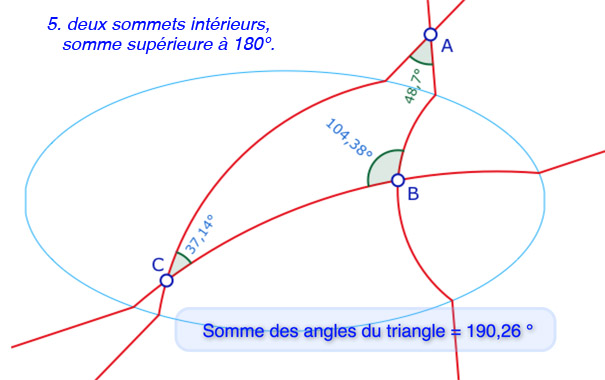
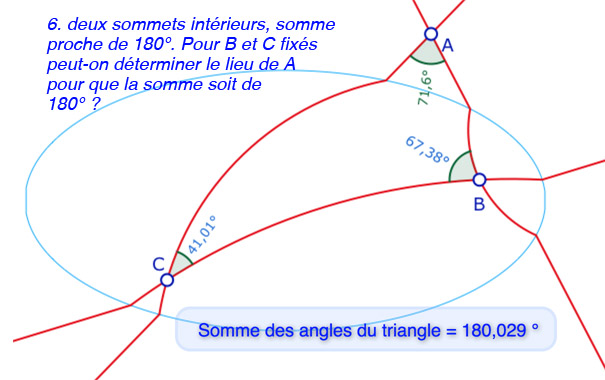
Cas d’un triangle ayant deux sommets à l’intérieur de l’ellipse
La géométrie dynamique permet de choisir une grande variété de paramètres, autres que les simples sommets sur lesquels on peut agir comme objets de base. C’est ce que l’on se propose de mettre en œuvre dans cette partie, qui est aussi l’occasion de montrer la richesse d’exploration, et une certaine simplicité de mise en oeuvre de la géométrie dynamique.
Plaçons nous dans le cas où les trois droites du triangle coupent l’ellipse. On choisit alors de les construire en se donnant comme point de base, les 6 points d’intersection des trois droites sur l’ellipse, en les nommant, comme dans les figures précédentes, \(Pg_{AB}, Qg_{AB}\), \(Pg_{AC}, Qg_{AC}\), \( Pg_{BC}, Qg_{BC}\). On s’intéresse au cas où un sommet seulement est extérieur à l’ellipse, disons le sommet \(A\). On construit ainsi les deux H-droites \((Pg_{AB} \; Qg_{AB})\) et\((Pg_{AC} \; Qg_{AC})\). Les points \(B\) et \(C\) sont construits comme intersection de ces deux droites avec la droite \((Pg_{BC} \; Qg_{BC})\)
Alors, sous réserve que les sommets \(B\) et \(C\) soient intérieurs à l’ellipse, on remarque que la somme des angles du triangle \(ABC\) ne dépend pas des positions de \(B\) et \(C\), c’est à dire de la droite \((BC)\) .
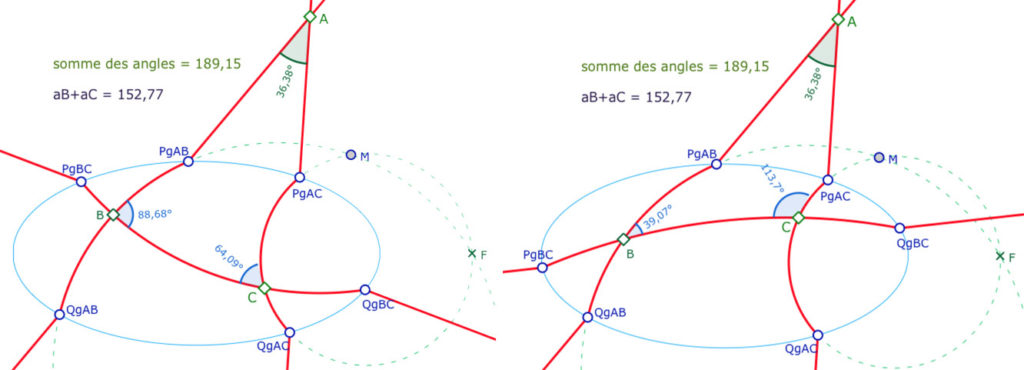
Manipulation d’une figure « de travail »
La figure proposée est seulement une « figure de travail » au sens où elle n’a pas été finalisée pour traiter tous les cas possibles. Elle est juste faite pour illustrer le propos. Ainsi les angles ne sont indiqués que par leurs mesures (pas la marque verte précise en \(B\) et \(C\)). Toutes les situations dynamiques ne sont pas traitées. En particulier, le point \(A\) doit rester au dessus de l’ellipse et donc les points \(Pg_{AB}\) et \(Pg_{AC}\) doivent rester d’ordonnées positives, soit au dessus de \(F\), et les points \(Qg_{AB}\) et \(Qg_{AC}\) d’ordonnées négatives (sous\(F\)) afin que \(A\) soit bien comme sur l’illustration, d’ordonnée positive.
Invariance de la somme \(aB+aC\) par rapport aux points \(Pg_{BC} , Qg_{BC}\).
Agir sur les 6 points sur l’ellipse en respectant les consignes de présentation de la figure.
Preuve de ce résultat
En fait, cette propriété est une simple conséquence d’une propriété déjà abordée.
Décontextualisons la figure, simplement en enlevant l’ellipse de référence. Désormais, on ne conserve que les points des droites qui définissaient le point \(A\) dans la figure précédente, que l’on a appelé ici \(p_{AB}, q_{AB}, p_{AC}, q_{AC}\). Les arcs des cercles passant par ces points et \(F\) représentent alors les parties des H-droites intérieures à l’ellipse. Sur ces deux arcs, on se donne les deux points \(B\) et \(C\). On a ainsi un autre type de manipulation directe.
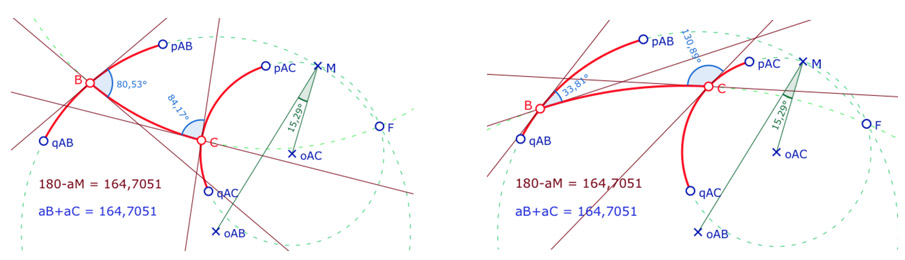
On se souvient alors que le triangle «intérieur», formé des arcs de cercles passant par \(F\), \(BCM\), a ses angles de somme un plat. Or, pour les 4 points \(p_{AB}, q_{AB}, p_{AC}, q_{AC}\) donnés, l’angle en \(M\) est constant, c’est aussi l’angle en \(M\) du triangle euclidien formé avec les deux centres de cercles, \(oAB\) et \(oAC\).
Et donc, la somme des angles en \(B\) et \(C\) est constante, ce qui explique cette propriété.
Manipulation de cette nouvelle figure, avec \(B\) et \(C\) en manipulation directe
On peut manipuler tous les points en gardant la «forme générique de la figure» propre à la situation étudiée,
en particulier les points définissant les arcs à gauche de \(F\).
C’est essentiellement une figure de travail. Agir en particulier sur \(B\) et \(C\).
Même contexte mais avec M comme point de base
Comme l’angle du triangle est lié au point \(M\), on peut choisir de rendre ce point manipulable dans une nouvelle figure que l’on replace dans le modèle de Hilbert. Voici les choix pour cette nouvelle figure (copie d’écran).
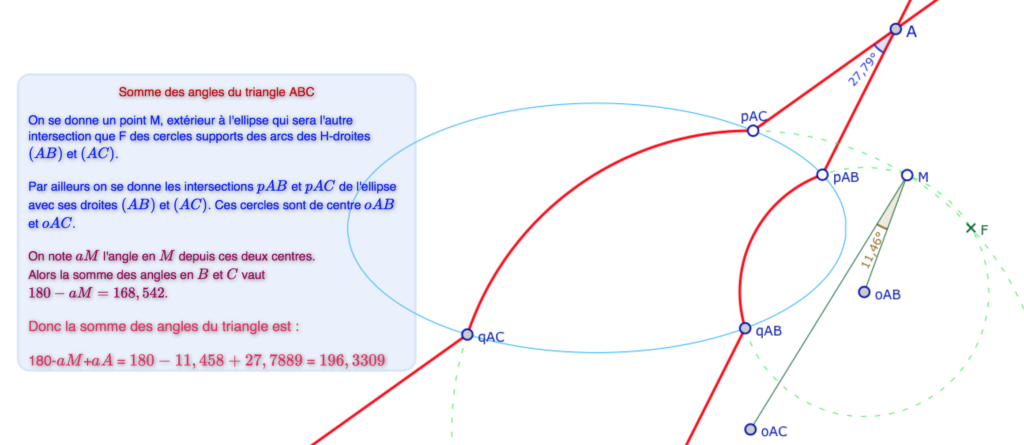
Dans les deux illustrations ci-dessous, on voit que cette possibilité d’agir sur le point \(M\) permet d’explorer autrement cette somme des angles. Sur l’illustration de droite, les points \(pAC\), \(qAC\) , \(M\) et \(F\) sont quasiment alignés … ce qui invite, à nouveau, à d’autres explorations.
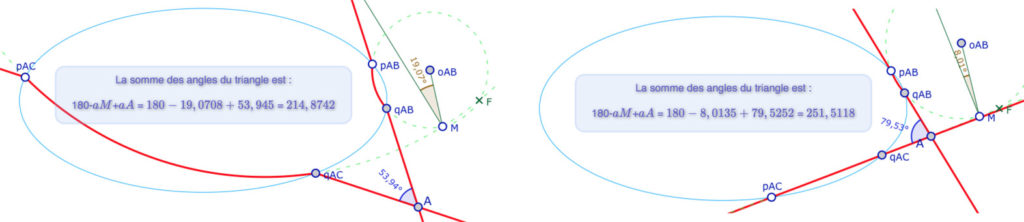
Manipulation de cette figure
Dans cette figure, on peut agir sur \(M, pAB, pAC\) et utiliser la case à cocher du widget pour afficher une droite \((BC)\) et agir sur les points \(B\) et \(C\).
Choisir d’ouvrir cette figure (sans restriction) dans un autre onglet
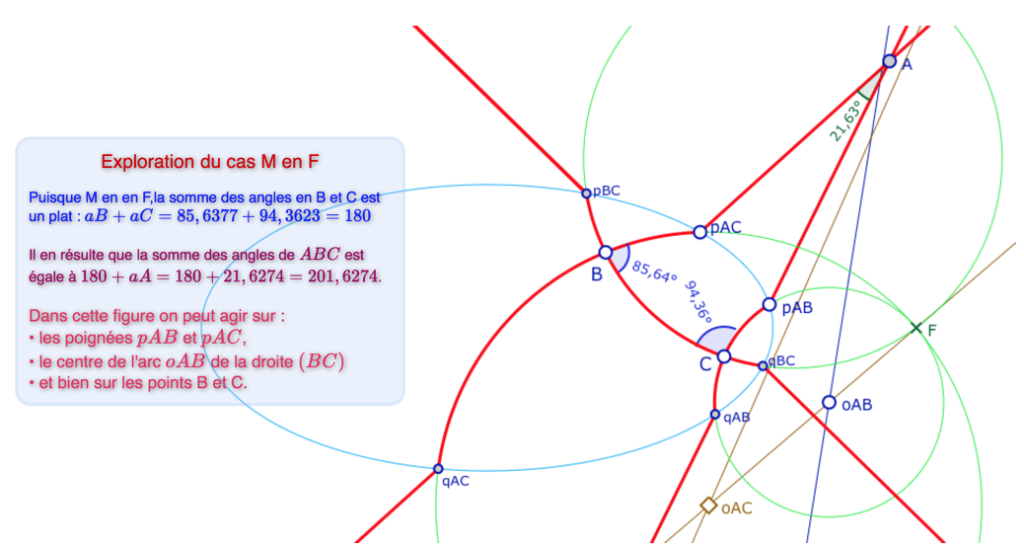
Cas particulier où \(M\) est en \(F\)
Plusieurs cas particuliers sont intéressants à étudier, comme \(M\) en \(F\), pour enlever l’angle \(aM\). En effet, si \(M\) est en\(F\), la somme des angles en \(B\) et\(C\) est un plat, donc la somme des angles est 180°+\(aA\).
La dynamique de la figure est à nouveau très différente de ce que l’on a fait jusque là. Soit un point de l’ellipse \(pAB\). On va pouvoir agir sur le centre du cercle support d’une des deux droites passant par \(A\) en prenant un point \(oAB\) sur la médiatrice de \(pAB\) et \(F\). En se donnant un point \(pAC\) sur l’ellipse, les droites \((AB)\) et \((AC)\) sont fixées car le centre \(oAC\) est à l’intersection de la droite \((oAB \; F)\) et de la médiatrice de \(pAB\) et \(F\). Cette nouvelle organisation dynamique de la figure permet d’obtenir autrement, par une action sur \(oAB\), des configurations proche des précédentes, quand l’angle \(aM\) était petit.
Cas \(M\) en \(F\) : les cercles supports des droites \((AB)\) et \((AC)\) sont tangents en \(F\).
Dans cette figure on peut agir sur les points \(pAB, oAB\) et \(pAC\).
Bref exploration pour minimiser la somme des angles avec deux points dans l’ellipse
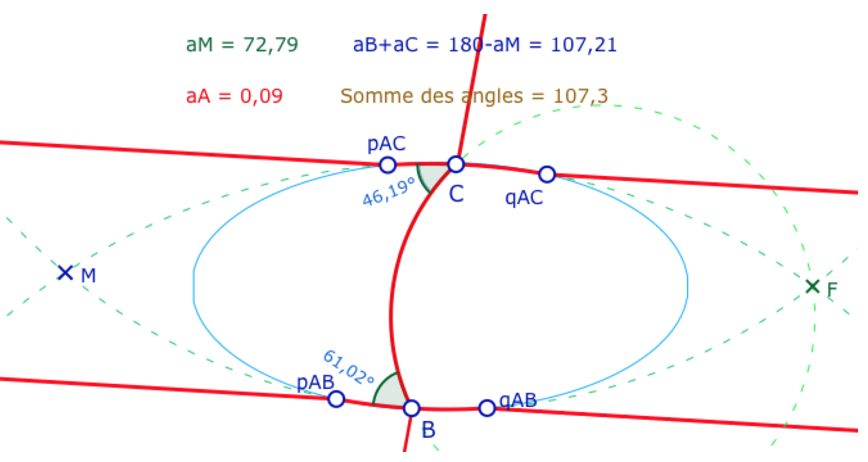
On reprend la figure générique précédente avec les droites passant par le sommet \(A\) pilotées par les quatre points de l’ellipse \(pAB, qAB, pAC, qAC\). Les sommets \(B\) et \(C\) sont encore pris sur les arcs de cercles des H-droites; ce sont les deux sommets intérieurs à l’ellipse, la figure suivante n’a de sens qu’en conservant le point \(M\) extérieur à l’ellipse.
Dans ce contexte, la somme du triangle est \(180°-aM+aA\). Pour chercher une somme minimale, il faut chercher à augmenter \(aM\) et diminuer \(aA\) même si les deux ne sont pas indépendants. L’idée est donc de rendre les droites \((AB)\) et \((AC)\) quasiment parallèles comme ci-contre où l’angle en \(A\) est proche de 0 tout en ayant une valeur de \(aM\) significative.
On peut manipuler les quatre poignées des droites sur l’ellipse ainsi que les sommets \(B\) et \(C\).
Si l’un de ces sommets se bloque sur une des poignées, l’arc peut «déraper» hors de l’ellipse.Il suffit juste de déplacer ce sommet pour que la figure reprenne une forme normale.