Hilbert considère le modèle de la géométrie euclidienne plane suivant. Il se donne l’ellipse centrée à l’origine du repère canonique, de grand axe 1 et de petit axe 1/2. Soit l’ellipse d’équation \(x^2+4y^2=1\). Puis il considère le point \(F \displaystyle \left( \frac{3}{2},0 \right)\) et montre que tout cercle passant par \(F\) et coupant l’ellipse, soit est tangent à l’ellipse, soit ne coupe l’ellipse qu’en deux points distincts. Plus précisément il montre que tout cercle coupant l’ellipse en 4 points ne passe pas par \(F\). Cela lui permet de définir une nouvelle géométrie de la façon suivante :
Droites et segments
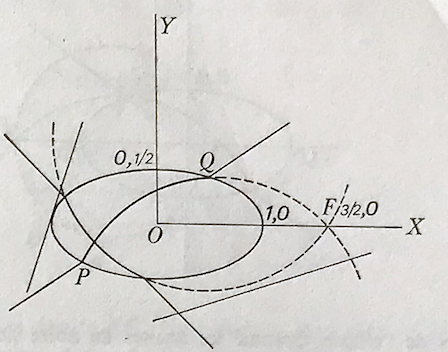
«Élaborons notre nouvelle géométrie comme suit. Comme points prenons les points du plan \(xy\). Comme droites, choisissons, sans modification, celles du plan qui ne coupent pas l’ellipse ou qui lui sont tangentes; par contre si une droite \(g\) coupe l’ellipse en deux points \(P\) et \(Q\), construisons le cercle passant par \(P\), \(Q\) et \(F\). Ce cercle ne coupe pas l’ellipse hors de ces points. Sur la droite \(g\) remplaçons le segment compris entre \(P\) et \(Q\) par l’arc du cercle précédent situé à l’intérieur de l’ellipse. Les deux demi-droites portées par \(g\) limitées à \(P\) et \(Q\) et l’arc de cercle ci-dessus constituent une droite de notre nouvelle géométrie(*). Supposons la construction effectuée pour toutes les droites du plan. Les droites de la nouvelle géométrie satisfont les axiomes (I.1 et I.2) et (IV). Les axiomes (II) sont aussi valables en considérant l’ordre naturel des points sur ces droites. Nous dirons que deux segments \(AB\) et \(A’B’\) sont congruents si les segments \(AB\) et \(A’B’\) mesurés éventuellement en tout ou partie sur un arc de cercle ont des longueurs habituelles égales. »
(*) Nous parlerons dans la suite de H-droite, pour droite de Hilbert, et de H-segment.
Les angles
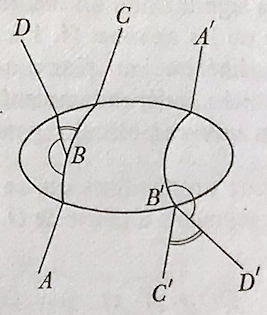
«Enfin il nous faut définir la congruence des angles. Si aucun des sommets des angles à comparer n’appartiennent à l’ellipse, nous dirons que les angles sont congruents s’ils le sont au sens ordinaire du terme. Dans le cas contraire, opérons comme suit :
Soient\(ABC\) et \(A’B’C’\) des points alignés ordonnés de notre géométrie, \(D\) un point extérieur à la droite \(ABC\) et \(D’\) hors de la droite \(A’B’C’\).
Nous dirons que les congruences suivantes d’angles sont satisfaites:
\(\angle ABD = \angle A’B’D’\) et \(\angle CBD = \angle C’B’D’\)
si les angles naturels correspondant sont liés par la proportion
\(\angle ABD : \angle CBD = \angle A’B’D’ : \angle C’B’D’\)
Grace à ces conventions les axiomes (III.1 à 4) sont valables.»
Entre les pages sur le modèle de Hilbert et celles sur le modèle de Moulton, nous proposons une « page interlude » analysant cette définition de la congruence des angles dont l’un a un sommet sur l’ellipse, en particulier car, comme l’a montré Moulton, elle ne vérifie pas vraiment l’axiome III.4 comme l’annonce un peu vite Hilbert.
Dans un premier temps, on retiendra que, pour les sommets hors de l’ellipse, les angles sont les angles euclidiens usuels.
La géométrie obtenue est non arguésienne
(exemple de Hilbert)
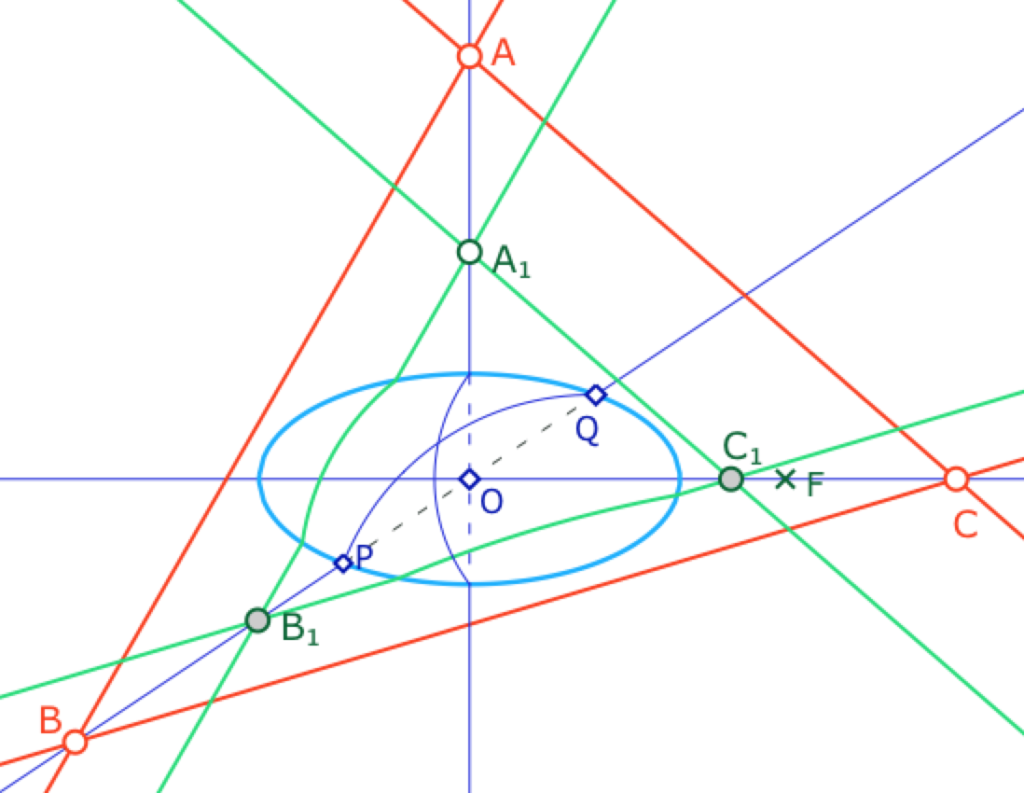
Pour illustrer que le théorème de Desargues n’est pas vérifié, Hilbert considère d’une part l’axe des abscisse – qui est une H-droite car cet axe est « le cercle » passant par F et les deux sommets de l’ellipse, puis la H-droite associée à l’axe des ordonnées et enfin celle passant par les points de l’ellipse \( \displaystyle \left( -\frac{3}{5},-\frac{2}{5} \right)\) et \(\displaystyle \left( \frac{3}{5},\frac{2}{5} \right)\). Or ces trois H-droites ne sont pas concourantes (se montre facilement). Il suffit alors de construire un triangle \(ABC\) avec un point sur chaque droite ainsi qu’un triangle\(A_1B_1C_1\) ayant ses côtés correspondants parallèles à ceux de \(ABC\) comme ci-contre pour illustrer que cette géométrie n’est pas arguésienne.
Dans les pages suivantes, nous allons nous intéresser tout d’abord à la construction dynamique de ces H-droites quand elles sont définies par deux points. Pour la construction des H-droites définies par deux points, on peut distinguer trois cas :
• Cas 1 : les deux points sont extérieurs à l’ellipse.
• Cas 2 : les deux points sont intérieurs à l’ellipse.
• Cas 3 : un des points est à l’intérieur, l’autre à l’extérieur.
Dans les deux premiers cas, on étudiera déjà quelques propriétés de la géométrie non arguésienne du modèle de Hilbert dans ces configurations spécifiques. Si les deux premiers cas relèvent d’une simple construction géométrique, le troisième cas qui pourtant n’est a priori qu’un problème du 4° degré, est nettement plus complexe à traiter et fera l’objet d’une approche particulière. L’objectif final étant bien entendu de proposer à l’utilisateur des figures dynamiques transparentes où les 3 cas sont regroupés.
Bien entendu, une H-droite ayant toujours deux points à l’extérieur de l’ellipse, on pourrait se dire qu’on peut tout réaliser de cette géométrie avec le simple premier cas. C’est assez implicite dans le texte de Hilbert. Mais d’un point de vue de la géométrie dynamique, puisqu’une droite est définie par deux points et que l’on veut pouvoir la manipuler par ces deux points, il est nécessaire de savoir construire les H-droites dans ces trois cas et que le passage d’un cas à l’autre soir totalement transparent.
Par ailleurs chacun de ces cas va permettre des explorations de la géométrie non arguésienne originales et même parfois surprenantes.
Droites cas 1 | Droites cas 2 | Droites cas 3
Complément
Page de présentation des macros permettant de réaliser des figures dans les cas 1 et 2.