Avant d’aborder d’autres géométries, que notre géométrie standard, dans des modèles euclidiens, voyons déjà notre géométrie euclidienne classique dans d’autres modèles que le plan usuel \(\mathbb{R} \times \mathbb{R}\) à travers un œilleton, dans un disque.
Définition du modèle DE (disque euclidien) – Aspect affine
On admet provisoirement – on le montrera un peu plus loin – que la définition suivante correspond bien à une géométrie euclidienne. Les points sont l’intérieur d’un disque. Le cercle frontière du disque correspond aux points à l’infini. Dans un éventuel prolongement projectif, le cercle serait la droite à l’infini. Cela signifie en particulier que deux droites parallèles vont se couper sur ce cercle horizon.
La droite \((AB)\) dans ce modèle (on dira DE-droite) est l’arc de cercle passant par \(A\) et \(B\) et coupant le cercle horizon en deux points diamétralement opposés. Bien entendu si \(A\) et \(B\) sont alignés avec le centre, l’arc devient un segment, c’est un diamètre du cercle. La construction de la DE-parallèle à \((AB)\) passant par \(M\) est alors immédiate, puisque l’on à trois points de sa représentation : les deux points de la DE-droite \((AB)\)) à l’infini – sur l’horizon – et le point \(M\).
Dans une situation affine, si on sait tracer la parallèle à une droite, on sait construire le milieu de deux points. Voyons cela.
Le DE-milieu \(I\) de \(A\) et \(B\) va s’obtenir comme intersection des DE-diagonales d’un DE-parallélogramme. On peut prendre un point \(C\) quelconque, mais pour transformer la figure en macro-construction, il est préférable de prendre un point construit. Ici \(C\) est le milieu (usuel) entre le centre de l’horizon et le milieu usuel de [AB]. Les DE-parallèles à \((AC)\) par \(B\) et à \((BC)\) par \(A\) se coupent en \(D\). \(I\) est l’intersection des deux DE-droites.
Applications immédiates : la droite des milieux et le théorème de Varignon
On transforme cette figure en macro, ce qui permet de réaliser les illustrations suivantes :
• à gauche, le théorème des milieux : la droite \((IJ)\) est parallèle à \((BC)\).
• à droite, le théorème de Varignon : le quadrilatère des milieux \(IJKL\) de \(ABCD\) est un parallélogramme. On voit que les droites sont bien deux à deux parallèles et parallèles à la diagonale.
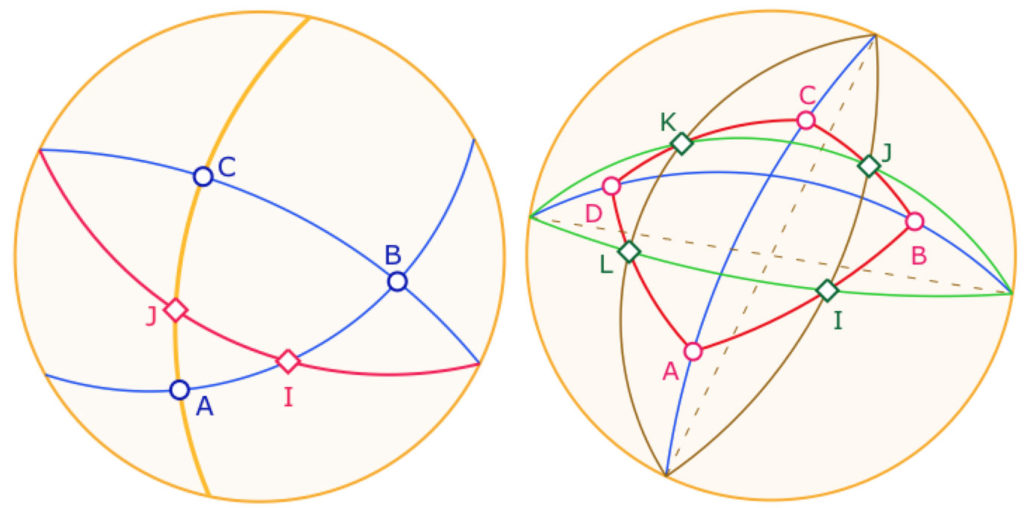
Sur la figure de droite, \((IJ)\) et \((AC)\) sont parallèles, et parallèle à la droite-diamètre (en pointillé) de mêmes extrémités à l’infini. Ainsi, deux droites perpendiculaires ont leurs droites-diamètres perpendiculaires, ce qui justifie la construction suivante.
Aspect euclidien
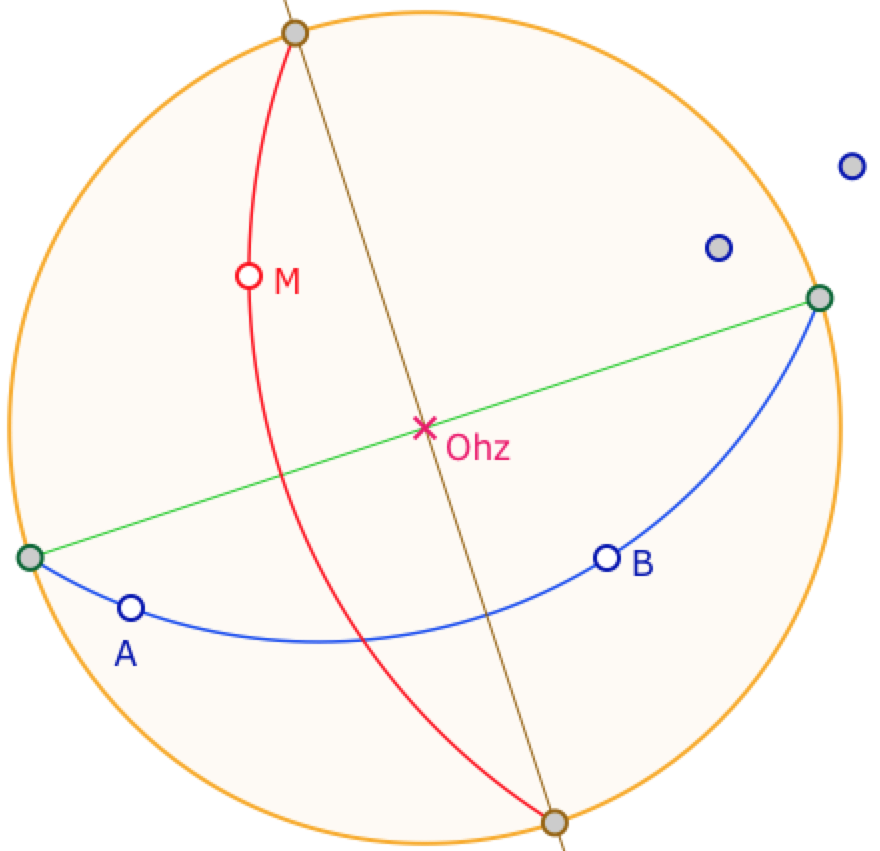
Le modèle n’est pas conforme – c’est-à-dire les angles dans le modèle ne sont pas égaux aux angles initiaux. En mathématiques, on préfère les modèles conformes car on peut continuer à faire fonctionner les représentations angulaires. Ici ce n’est pas le cas.
Le modèle n’est pas conforme sauf en l’origine du disque (commentaire de la figure précédente).
Cette conformité en l’origine du cercle permet de construire tout simplement la perpendiculaire à une droite passant par un point, comme ci-contre celle à \((AB)\) passant par \(M\).
On a laissé les points de construction de la DE-droite : le symétrique de \(A\) par rapport au centre \(kz\), puis l’inverse de ce point par rapport à l’horizon : le cercle support de la DE-droite passe par cet inverse, \(A\) et \(B\).
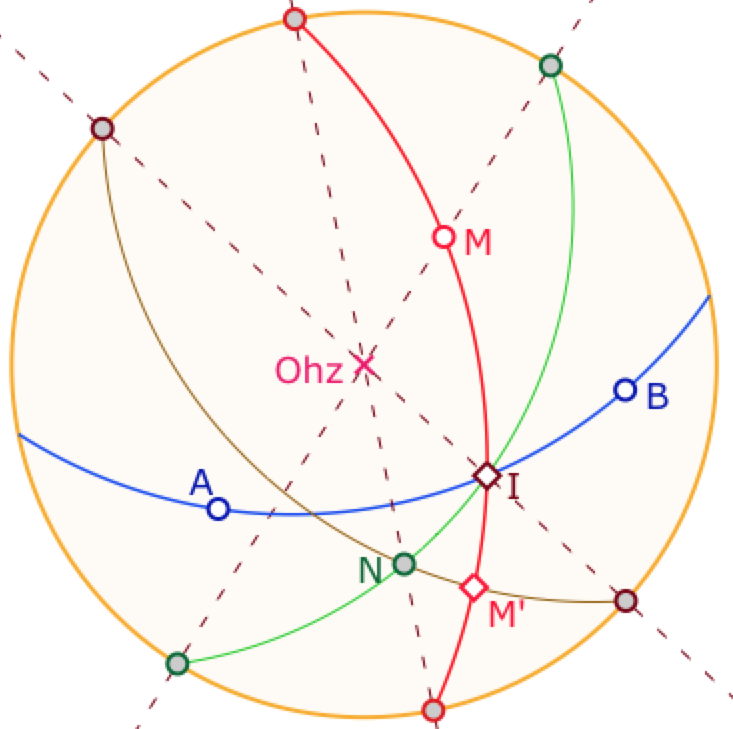
Du milieu au symétrique orthogonal d’un point par parallélogrammes
On se donne une droite \((AB)\) et un point \((M\). Il s’agit de construire le symétrique \((M’\) de \((M\) par rapport à \((AB)\). La perpendiculaire à \((AB)\) passant par \((M\) coupe (AB) en \(I\). Comme \(I\) doit être milieu de \((M\) et \((M’\) on peut construire, à partir d’un point \(C\), un premier parallélogramme \(CMIN\), avec \(CN=IM\), et plus précisément \(\overrightarrow{CN}=\overrightarrow{MI}\), puis un second parallélogramme NCIM’, avec \(\overrightarrow{IM’}=\overrightarrow{CN}\).
Pour simplifier la construction – et optimiser le nombre d’objets intermédiaires – on peut choisir pour C le centre Ohz du disque euclidien. Ici les DE-parallèles sont les segments supports passant par le centre \(Ohz\) : la DE-parallèle à \((MI)\) passant par \(Ohz\) est le diamètre support de la DE-droite, d’où l’économie d’objets.
Bel exemple de l’usage des parallélogrammes mais aussi des spécificités d’un modèle pour optimiser les macro-constructions.
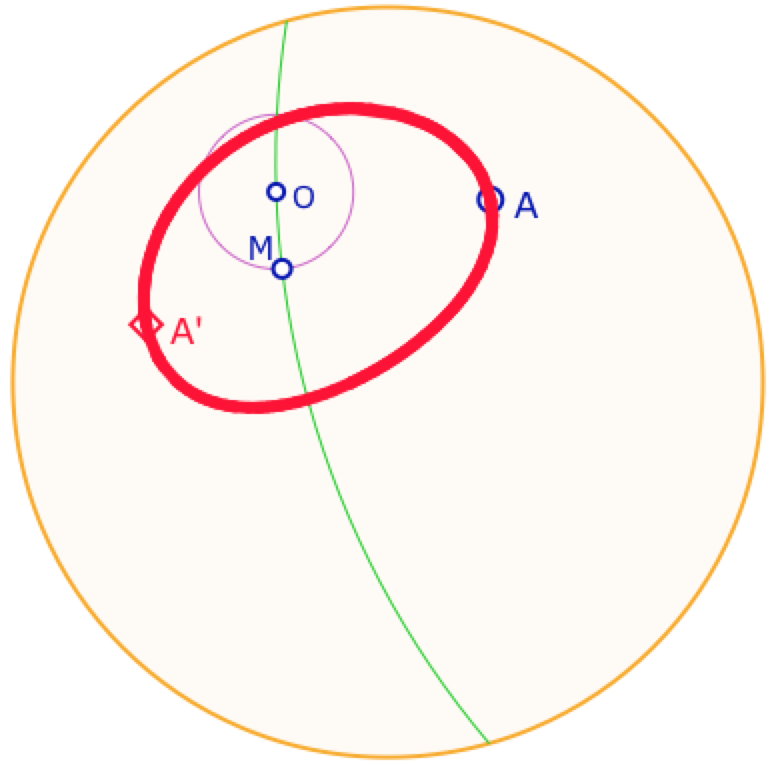
De la symétrie orthogonale au cercle
Dans l’approche axiomatique qui soutient cette présentation, le cercle de centre \(O\) passant par \(A\) est l’ensemble des points images de \(A\) par toutes les symétries orthogonales de droites passant par \(O\) (on parlera plus tard d’un faisceau à centre). Pour le construire on peut faire un lieu – ci-contre une trace – avec un point \(M\) qui tourne autour de \(O\).
Dans ce modèle, la représentation d’un DE-cercle n’est ni un cercle euclidien, ni une ellipse, mais un lieu plus complexe. Il en résulte en particulier que l’intersection de deux cercles – par exemple pour construire une tangente issue d’un point – ne va pas être facile à obtenir. On peut alors réfléchir à une autre approche.
Celle que l’on vient d’explorer a montré qu’avec peu de choses, on peut construire les premiers outils géométrique.
Allons désormais un peu plus loin.
Homéomorphisme du plan euclidien sur le disque unité
La conjugaison comme procédé de transfert
Une autre solution pour réaliser des figures complexes dans ce modèle est de les réaliser par conjugaison. C’est un procédé général déjà largement utilisé, par Steiner par exemple : pour construire l’ellipse de Steiner, on la réalise sur un triangle équilatéral – c’est le cercle inscrit – que l’on déforme par une application affine. Transposé dans une problématique de géométrie dynamique, on utilise une vraie conjugaison au sens où étant donnés des points de base dans le disque, que l’on pourra modifier en manipulation directe, on envoie ces points dans une géométrie plus connue. On fait la figure voulue dans cette géométrie, et on la renvoie dans la géométrie étudiée, ici le disque de géométrie euclidienne bornée.
Ce procédé est aussi celui utilisé par Beltrami pour étudier la géométrie intrinsèque de la pseudosphère : il utilisait un disque intermédiaire. C’est dans ce disque que Klein a vu le premier modèle borné de tout le plan hyperbolique. Tout, car la pseudosphère de Beltrami ne représentait qu’une partie du plan hyperbolique. Ce thème est abordé dans le menu PS.
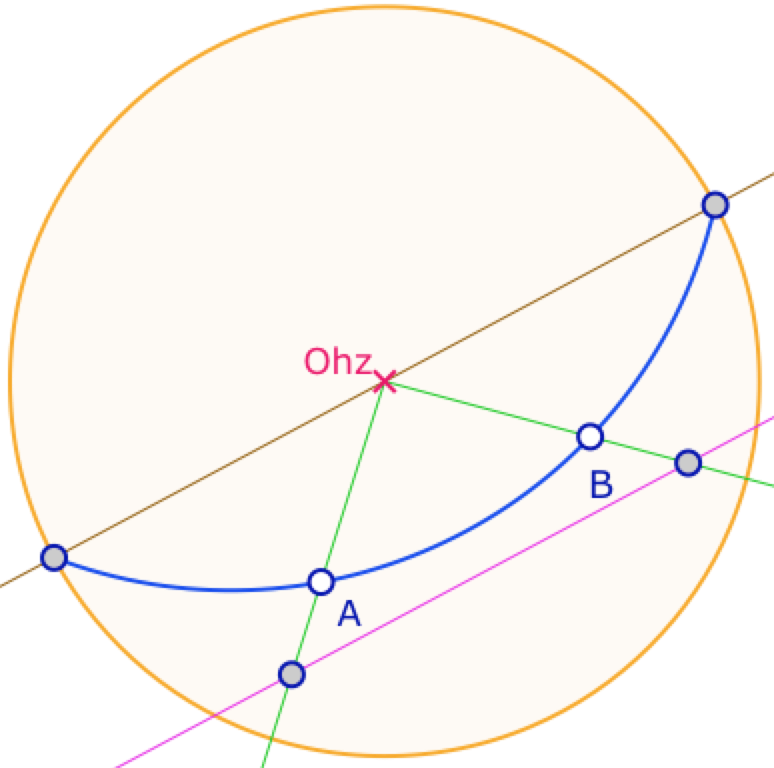
Du disque au plan
Parmi les homéomorphismes élémentaires qui permettent de passer du disque unité au plan euclidien, intéressons nous à celui-ci, \( \Phi(X,Y)=(x,y)=\left( \frac{X}{1-X^2-Y^2}, \frac{Y}{1-X^2-Y^2}\right)\) . Le cercle d’équation \(X^2+Y^2+uX+vY-1=0\) coupe le cercle unité selon la droite \(ux+vy=0\), donc en deux points diamétralement opposés, et ce cercle est envoyé par \(\Phi\) sur la droite d’équation \(ux+vy-1=0\). Alors toute droite parallèle \(ux+vy=w=0\) est l’image d’un cercle qui coupe le cercle unité en les deux mêmes points : c’est le parallélisme comme présenté précédemment.
Ce même calcul justifie également l’orthogonalité comme on l’a construit sur la base de l’orthogonalité des supports en l’origine.
Tout ceci suppose que le cercle est désormais le cercle unité.
Du plan au disque
Pour aller de \((x,y)\) dans le plan euclidien à \((X,Y)\) dans le disque unité tel que \((x,y)=\Phi(X,Y)\), on commence par exprimer \(R^2=x^2+Y^2\) à partir de \(r^2=x^2+y^2\) et ensuite, on a tout simplement \(X=x(1-R^2)\)et \(Y=y(1-R^2)\). Or la relation \(\Phi\) se traduit par \(R^2r+R-r=0\), ce qui donne \(R=\frac{-1+\sqrt{4r^2+1}}{2r}\). On a donc le retour de la conjugaison dans le disque. Ce qui permet de construire le milieu de 2 points en trois objets intermédiaires (\(A’, B’\) et son milieu \(I’\)), et le cercle de centre \(O\) passant par \(A\) en 4 objets intermédiaires au lieu de plusieurs dizaines dans la version précédente. Cela permet aussi de construite les cercles et leurs intersections. Voici trois premières applications.
Le théorème du pivot
Dans un triangle \(ABC, P, Q\) et \(R\) sur les côtés, alors les cercles circonscrits, comme ci-dessous sont concourants.
C’est une conséquence de la caractérisation de la cocyclicité par les angles de droites. Nous verrons plus loin un cas particulier.
Exemple des tangentes communes à deux cercles
La construction est un classique de géométrie affine dans un contexte euclidien. On sait tracer les tangentes à un cercle issues d’un point extérieur. On sait que cela nécessite l’intersection de deux cercles. Les tangentes communes à deux cercles (ici de rayons différents) sont les tangentes à l’un des cercles issues de l’un des centres d’homothétie des deux cercles, ci dessous les points \(I\) et \(J\).
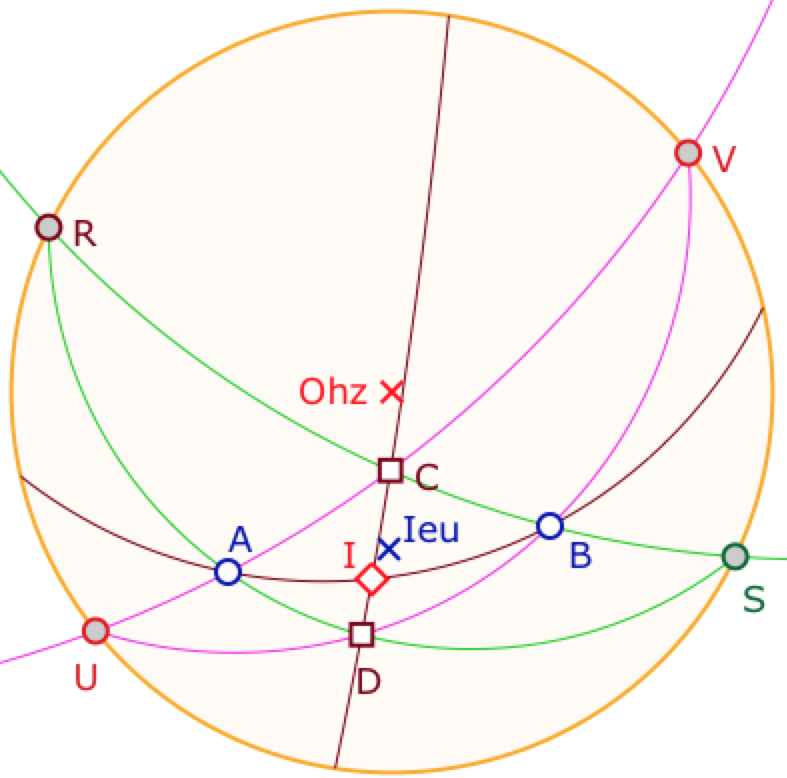
Le théorème de Feurerbach
Toujours sur les cercles, en introduisant les bissectrices, voici une figure plus consistante.
Le cercle d’Euler – le cercle des milieux (en bleu ci-dessous) est quadritangent au cercle inscrit (rouge) et aux trois cercles exinscrits (en marron foncé).
Les bissectrices intérieures sont roses, les extérieures vertes.
En pointillé les droites perpendiculaires pour le point de contact du cercle avec le côté du triangle.