Soit une H-droite \((AB)\) coupant l’ellipse du modèle, on cherche à partitionner le plan en régions en fonction du nombre de droites perpendiculaires à \((AB)\) et de leurs types (hilbertienne ou euclidienne) que l’on peut mener depuis les points de ces régions.
Notations associées au régionnement
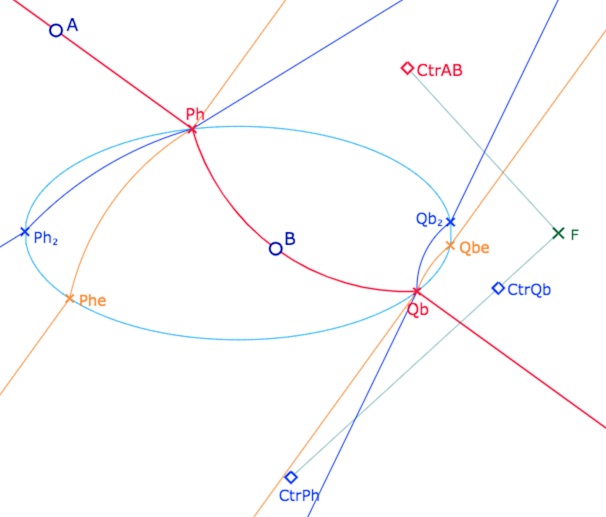
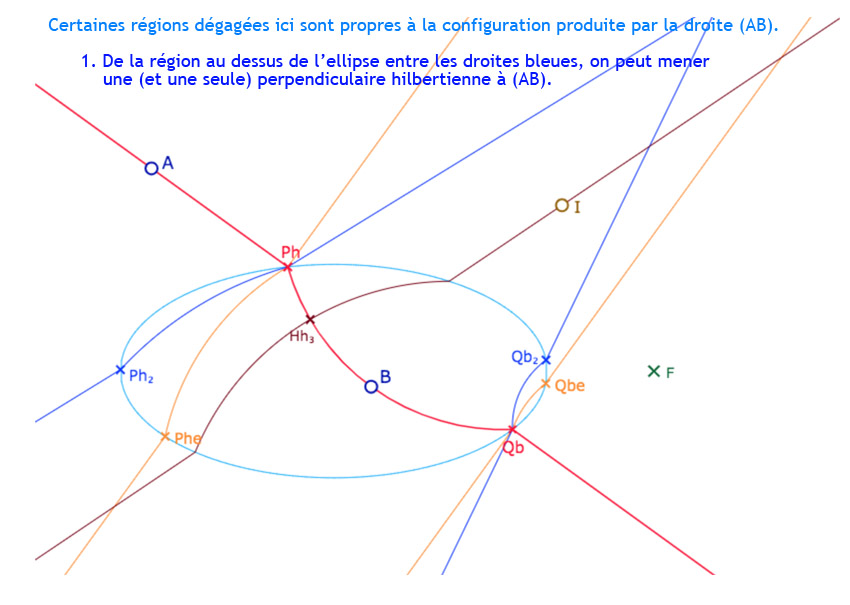
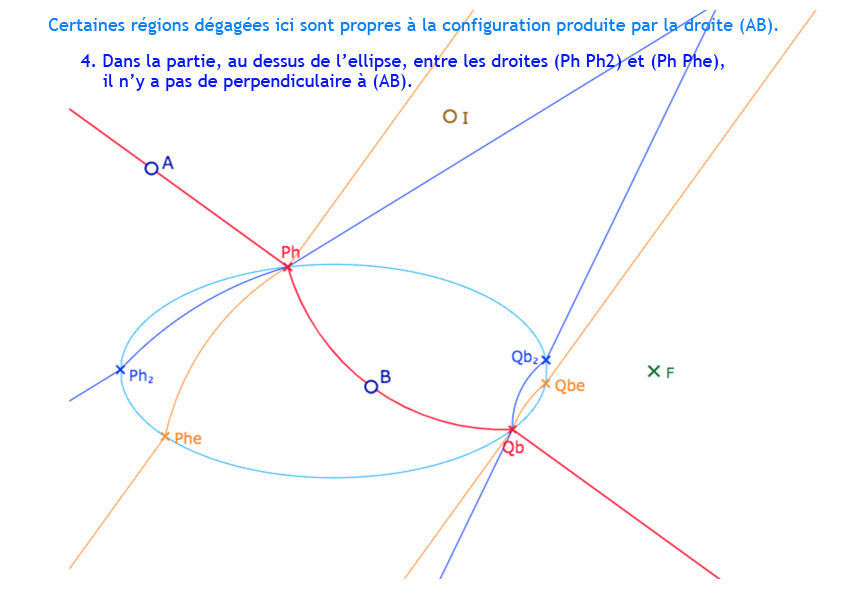
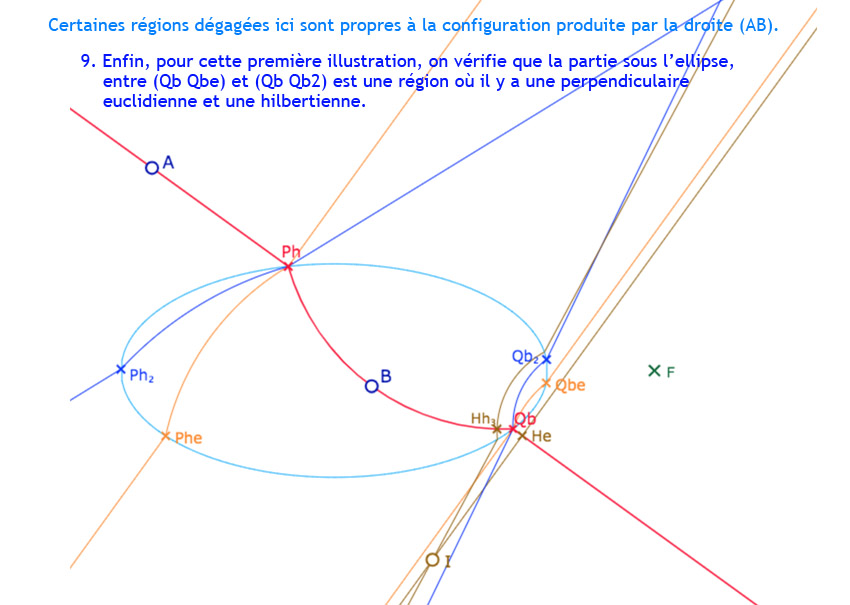
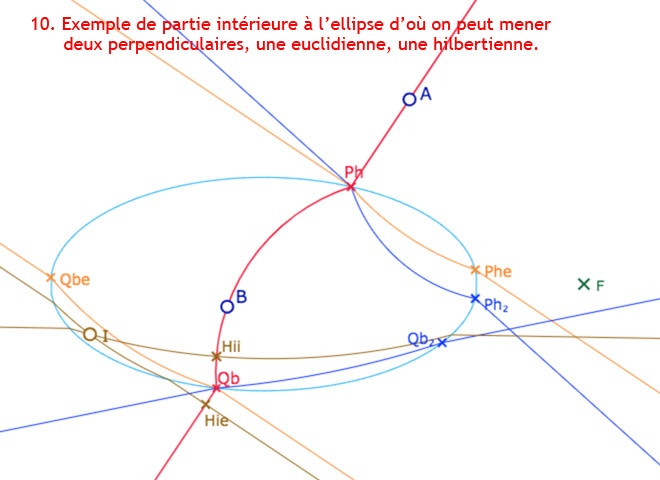
La droite \((AB)\) coupe l’ellipse en les points \(P_h\) et \(Q_b\). On note \(Ctr_{AB}\) le centre euclidien de la partie intérieure à l’ellipse de la droite, puis \(Ctr_{P_h}\) et \(Ctr_{Q_b}\) et les centres euclidiens des parties intérieures à l’ellipse des H-perpendiculaires à \((AB)\) en \(P_h\) et \(Q_b\). On construit ainsi les droites \((P_h \, P_{h_2})\) et \((Q_h \, Q_{h_2})\) les deux perpendiculaires hilbertiennes à \((AB)\) en \(P_h\) et \(Q_b\) (droites en bleu).
Il en résulte que toute perpendiculaire à \((AB)\) en un point de la droite entre \(P_h\) et \(Q_b\) a son centre euclidien entre \(Ctr_{P_h}\) et \(Ctr_{Q_b}\).
Puis on construit \((P_h \, P_{he})\) et \((Q_h \, Q_{he})\) les perpendiculaires euclidiennes à \((AB)\) en \(P_h\) et \(Q_b\), avec l’angle droit – extérieur à l’ellipse – en les points \(P_h\) et \(Q_b\) (droites en orange).
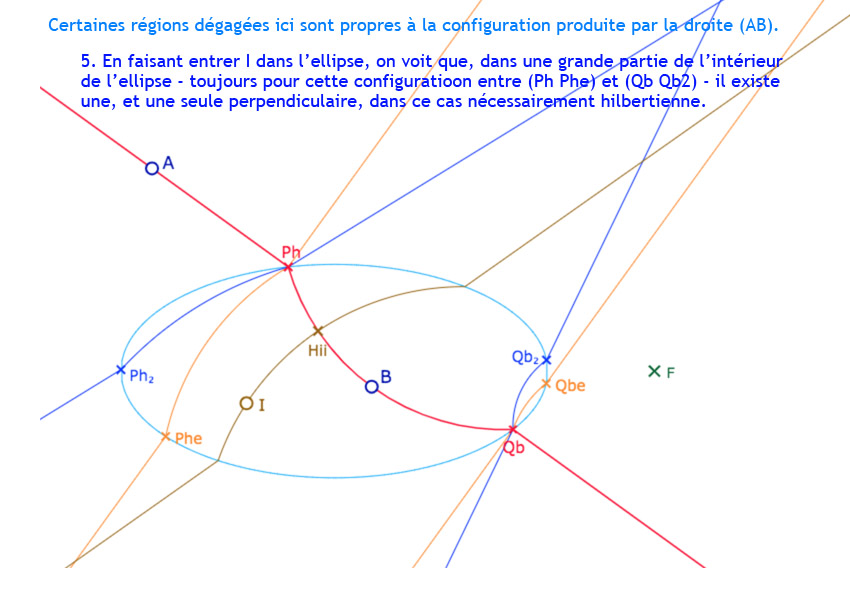
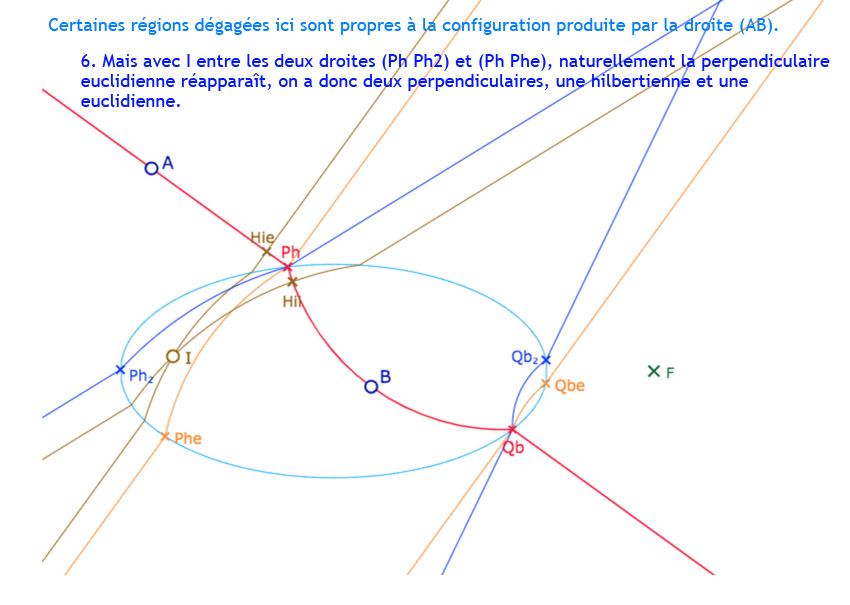
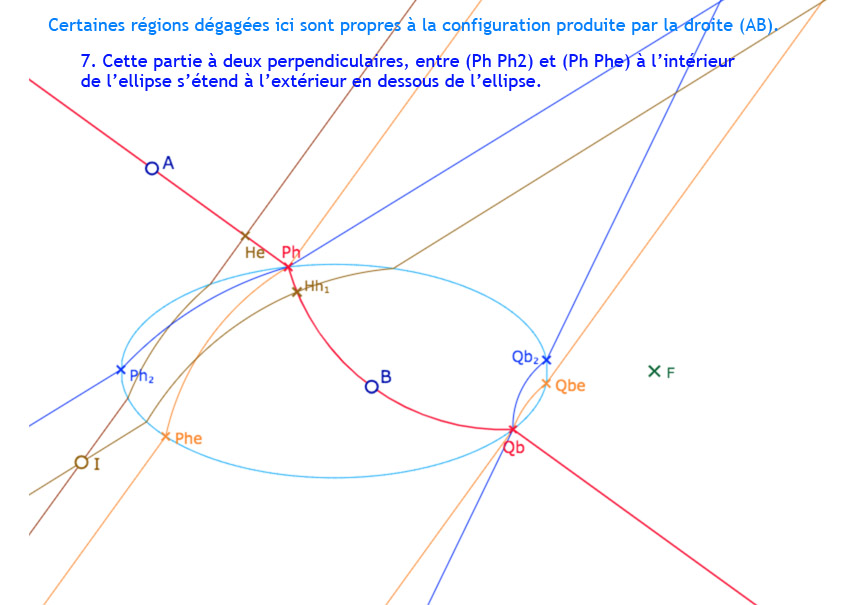
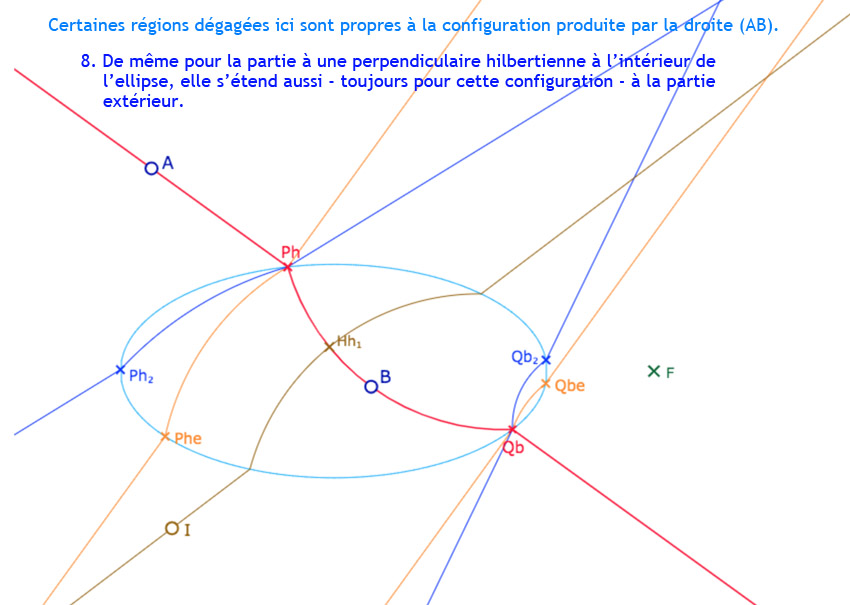
Ces cinq premières droites vont permettre de repérer les principales régions recherchées. Nous allons explorer cela en ajoutant un point \(I\) et les perpendiculaires à \((AB)\) issues de ce point. et voir aussi que … ce n’est pas aussi simple … bien entendu …
Dans une première galerie ci-dessous, quelques exemples de situations que l’on peut tester dans la figure suivante
Galerie 1 – 9 illustrations
Première figure dynamique d’exploration
Sur la figure précédente, on peut aussi tester des positions comme celles de cette nouvelle galerie
Galerie 2 – 5 illustrations
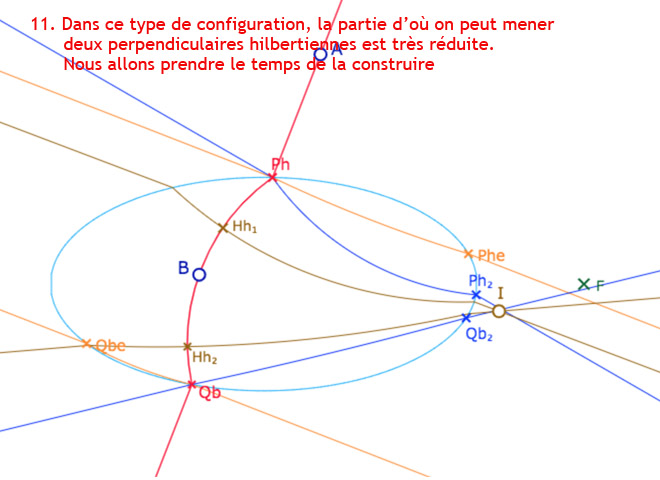
Frontière de la région des deux perpendiculaires hilbertiennes
Réalisation par lieu
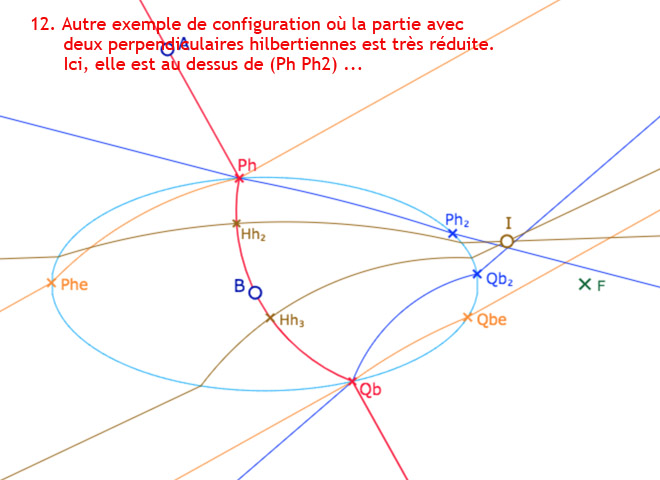
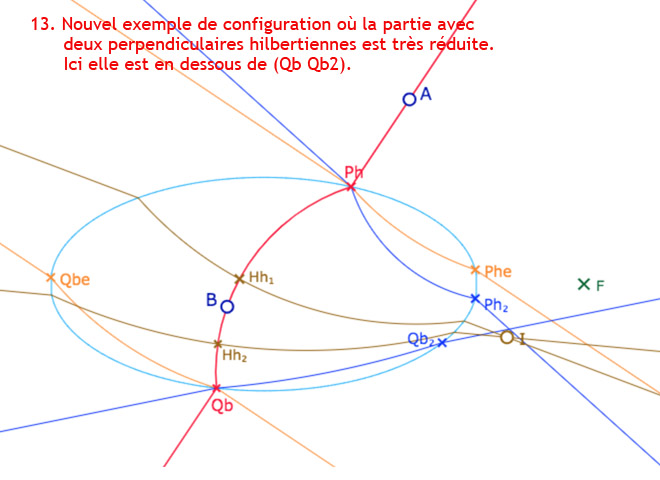
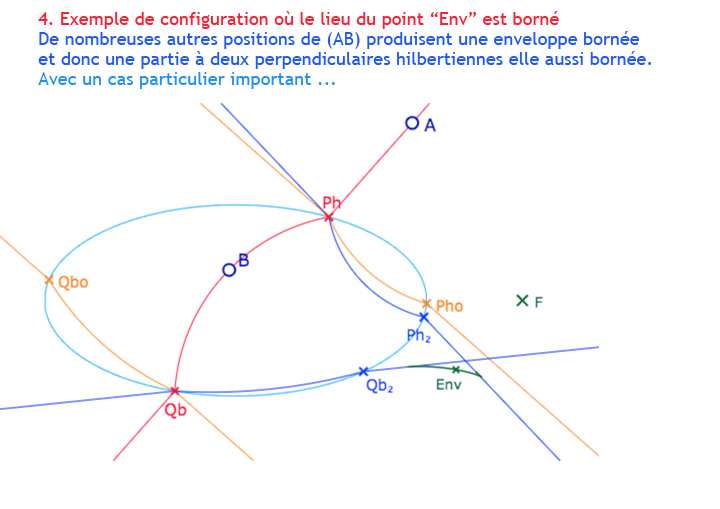
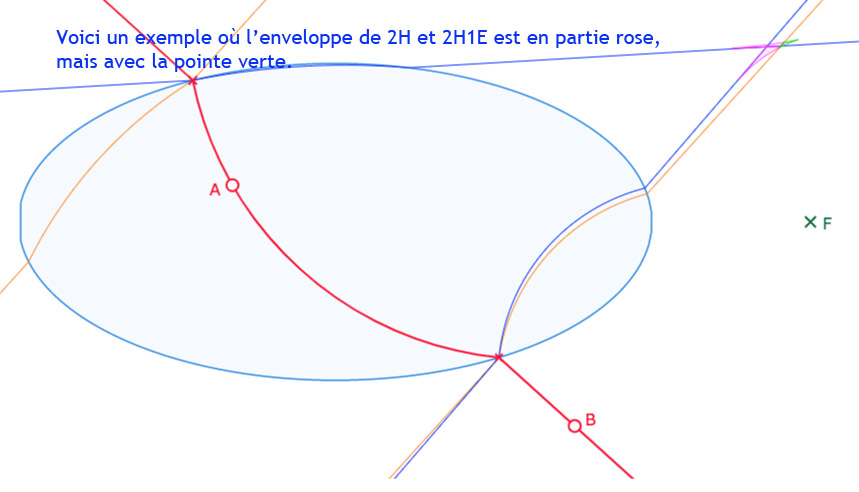
Comme observé avec la figure précédente, il y a une frontière non rectiligne entre une région à deux perpendiculaires hilbertiennes et une région sans perpendiculaire hilbertienne. Dans cette section, on propose une première exploration cette question.
Construction de la limite de la partie à deux perpendiculaires hilbertiennes
Les calculs algébriques relevant de ce sujet aboutissent à une fonction implicite particulièrement complexe, impossible à mettre en œuvre algébriquement dans le cadre de la géométrie dynamique. On va donc construire une approximation, qui sera précise au dixième de pixel, ce qui sera suffisant pour, ensuite, séparer les régions. L’exploration de cette frontière va permettre de mettre en évidence de nouvelles configurations autour de l’orthogonalité.
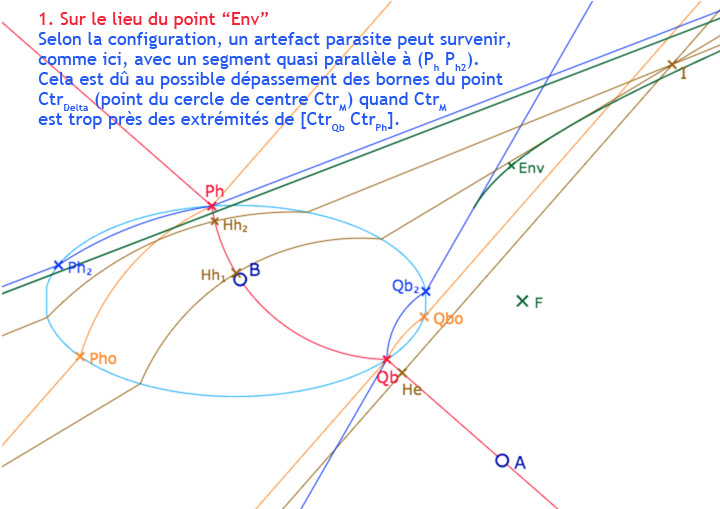
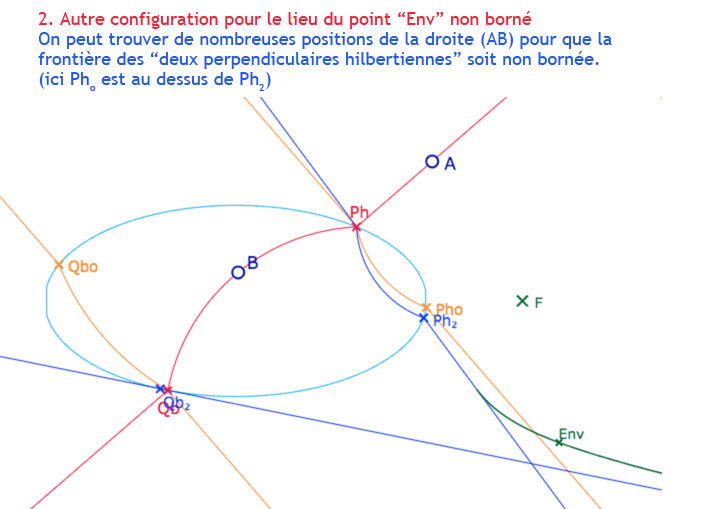
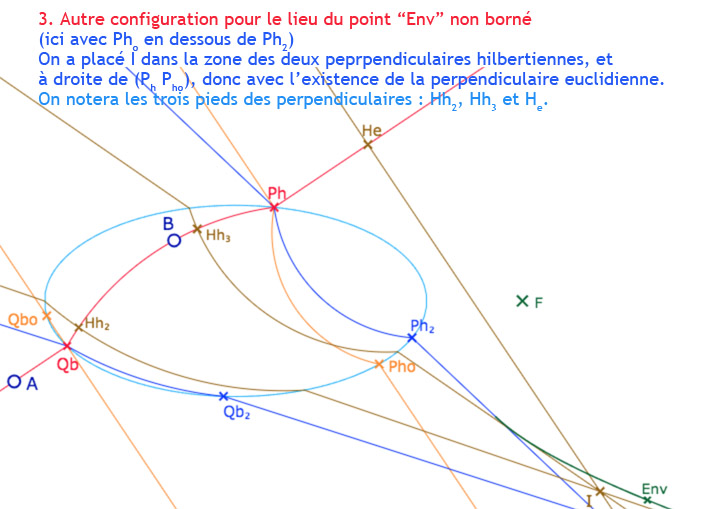
On se donne un point \(Ctr_M\) entre \(Ctr_{P_h}\) et \(Ctr_{Q_b}\) et on construit la perpendiculaire à \((AB)\) dont le centre euclidien de la partie à l’intérieur de l’ellipse est \(Ctr_M\). Puis, en prenant un point \(Ctr_{Delta}\), proche de \(Ctr_M\), on construit une seconde perpendiculaire à \((AB)\). Ces deux droites se coupent en un point nommé ci-dessous \(Env\) (pour « Enveloppe » du point) dont on va faire le lieu quand \(Ctr_M\) parcourt le segment \([Ctr_{P_h}Ctr_{Q_b}]\). Voici une illustration grossière avec un point \(Ctr_{Delta}\) volontairement éloigné de \(Ctr_M\) pour bien distinguer la première perpendiculaire (vert clair) issue de \(Ctr_M\) et la seconde (marron pointillé) issue de \(Ctr_{Delta}\). La frontière cherchée est alors le lieu du point \(Env\), en vert foncé.
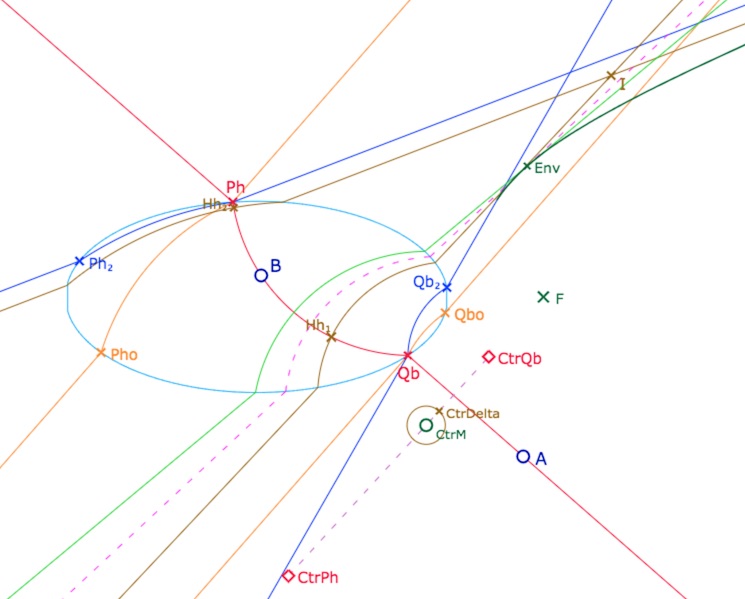
Principe de construction (avec un rayon de cercle en \(Ctr_M\) grand pour distinguer les deux perpendiculaires.
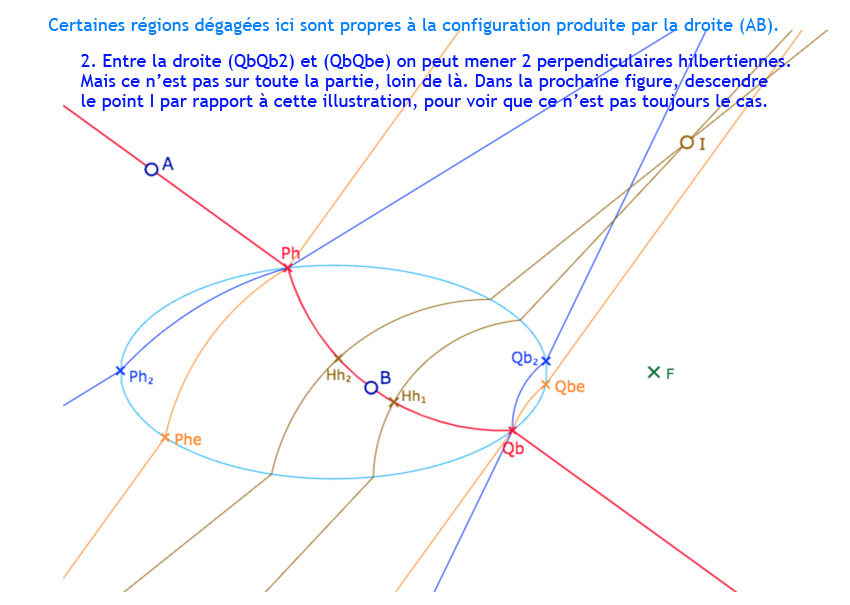
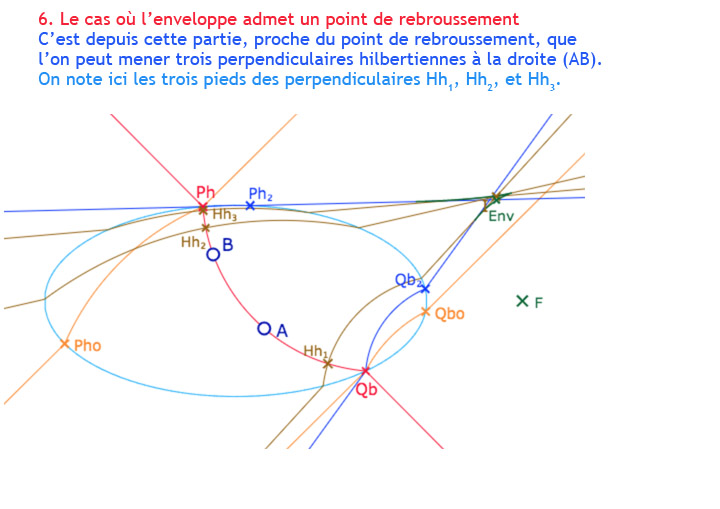
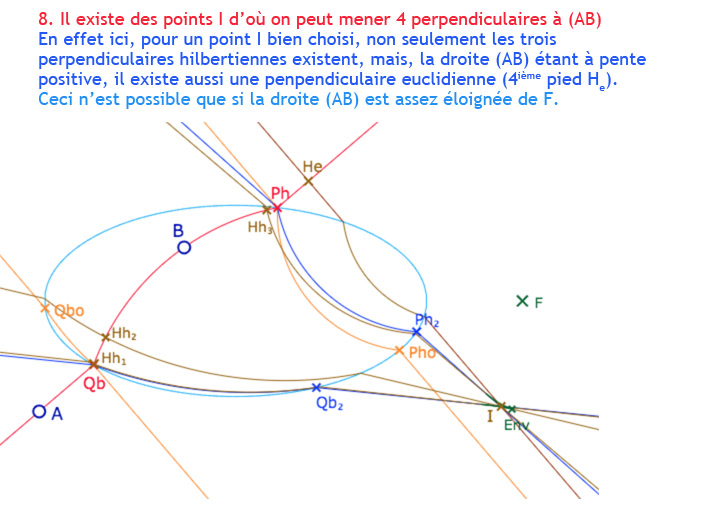
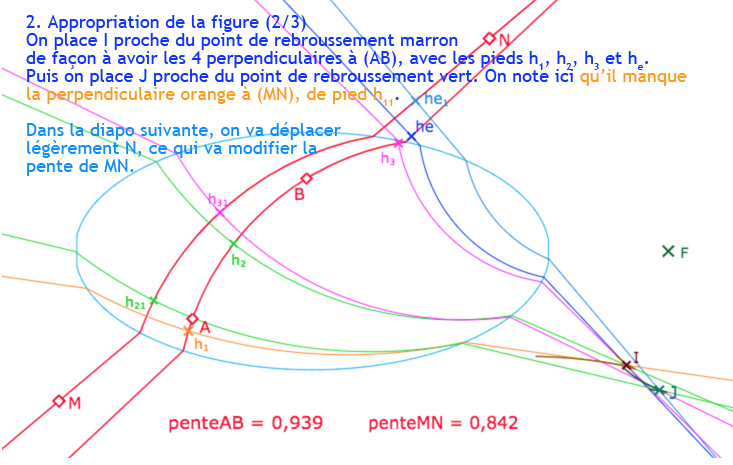
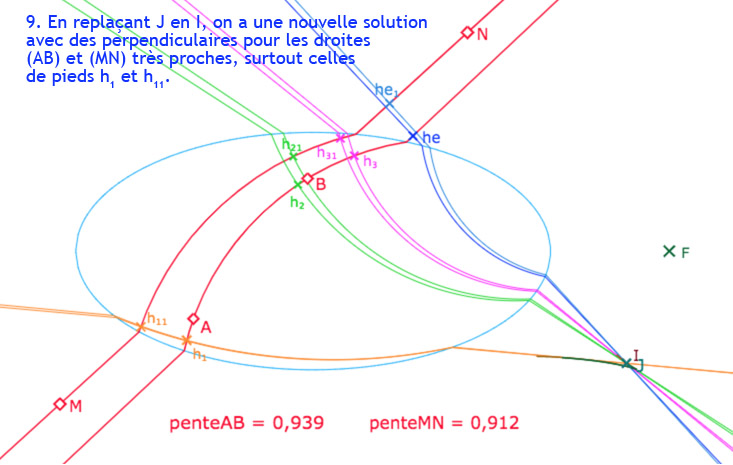
On a ajouté un point \(I\) et les perpendiculaires à \((AB)\) issues de ce point. Dans l’illustration, \(I\) est dans la partie à deux perpendiculaires hilbertiennes, de pieds \(H_{h_1}\) et \(H_{h_2}\).
Voici maintenant une illustration de la figure avec une distance entre les points \(Ctr_M\) et \(Ctr_{Delta}\) de \(10^{-4}\), soit en pratique, inférieure à 1/10 de pixel. Les deux perpendiculaires semblent être l’une sur l’autre (c’est pour cela que l’une est en pointillé), mais elles diffèrent légèrement, d’où l’existence du point \(Env\)
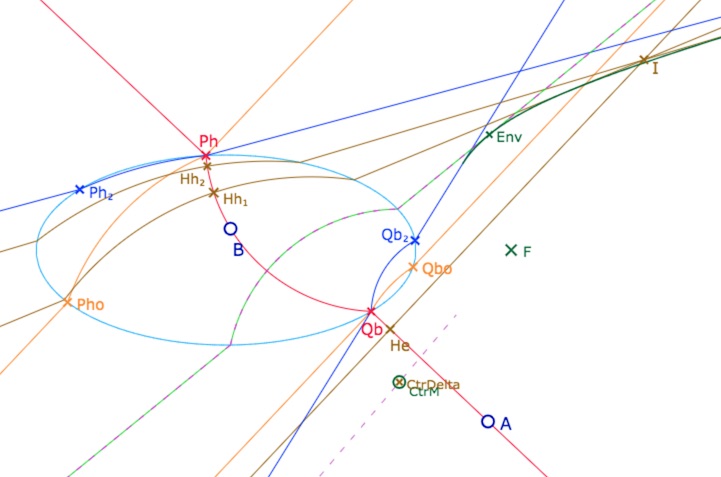
Frontière entre deux perpendiculaires hilbertiennes et aucune, avec une plus grande précision.
Cette fois, \(I\) étant (dans cette configuration s’entend) à droite de \((Q_bQ_{bo})\), il existe en plus une perpendiculaire euclidienne, de pied \(H_e\).
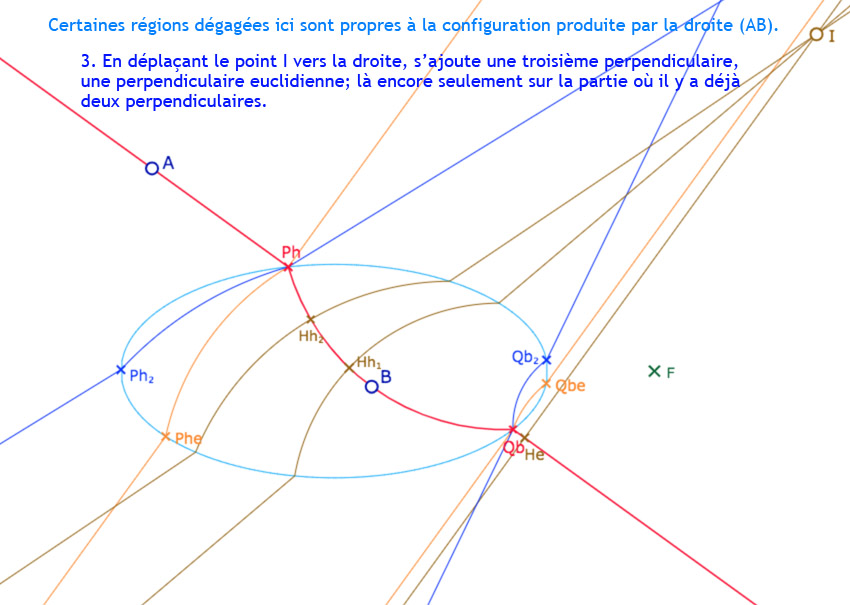
Cas de droites admettant 4 perpendiculaires issue d’un point
Avant de proposer la manipulation de cette figure, voici une galerie de quelques configurations que l’on peut explorer.
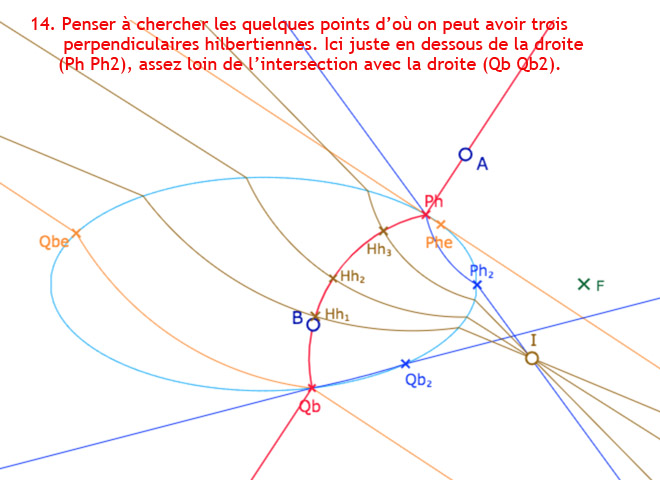
Configurations diverses sur la frontière des deux perpendiculaires hilbertiennes.
Avec comme conséquence, des points d’où on peut mener 4 perpendiculaires à une droite.
On a déjà présenté une animation automatique de droites ayant ainsi 4 perpendiculaires issues d’un même point. Elle est dans la page d’introduction à l’orthogonalité, mais a été mise en évidence lors de la rédaction de cette page.
Figure dynamique associée
Si la figure est longue à charger, ne pas hésiter à cliquer (souvent deux fois) sur l’icone de recharge de l’iframe.
A l’ouverture, le rayon du cercle est de 1/10. Commencer par le réduire à 1/10000 avec le pop up. On peut ensuite déplacer le commentaire vers le haut pour avoir plus de place pour la manipulation. On déplace la figure simplement à la souris dans la fenêtre.
Explorer les différentes options présentées dans la galerie précédente.
Et en particulier, chercher obtenir le cas de 4 perpendiculaires à \((AB)\) issues de \(I\)
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Première application de ce lieu
Dans cette section on propose de manipuler une figure pour arriver à ce résultat : placer un point \(I\) d’où on peut construire 4 perpendiculaires, respectivement, à deux droites non parallèles, comme ceci :
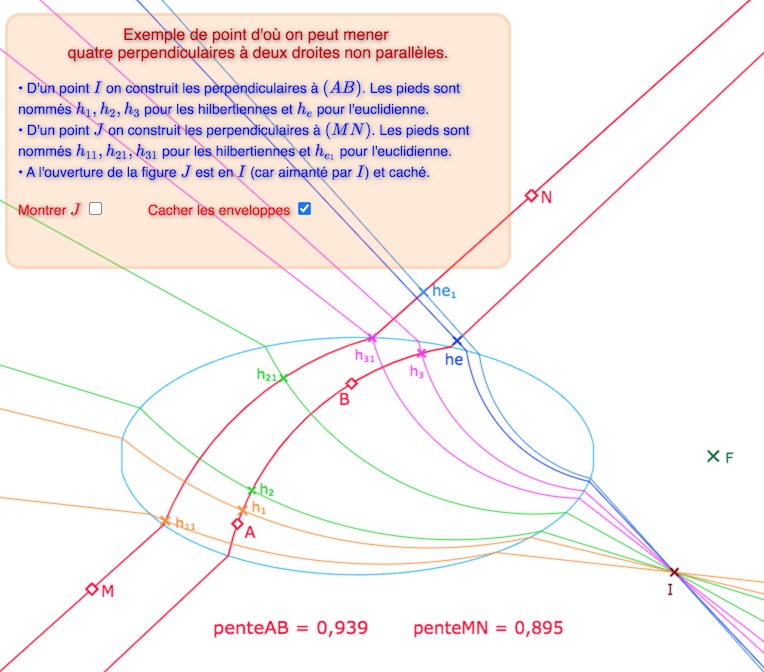
Objectif de cette section : manipuler une figure pour obtenir ce type de résultat
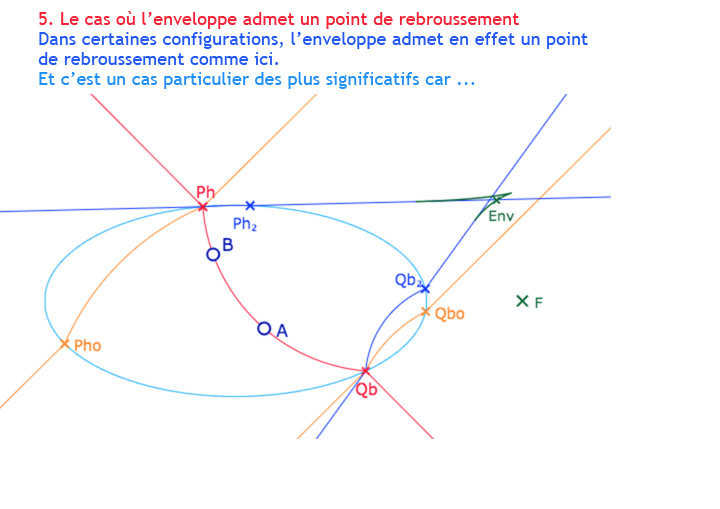
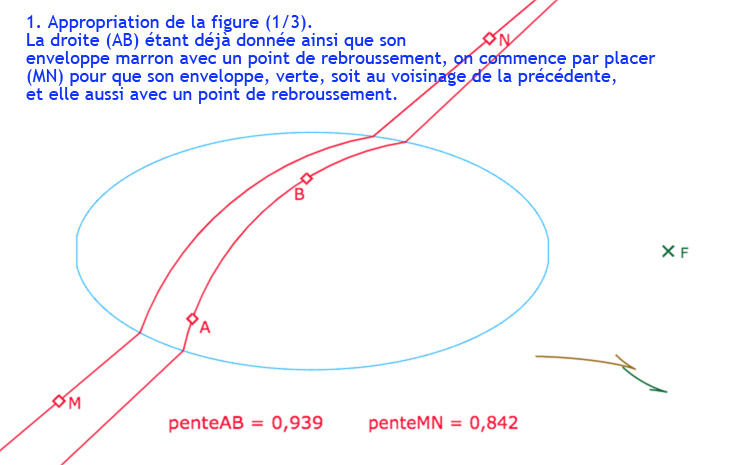
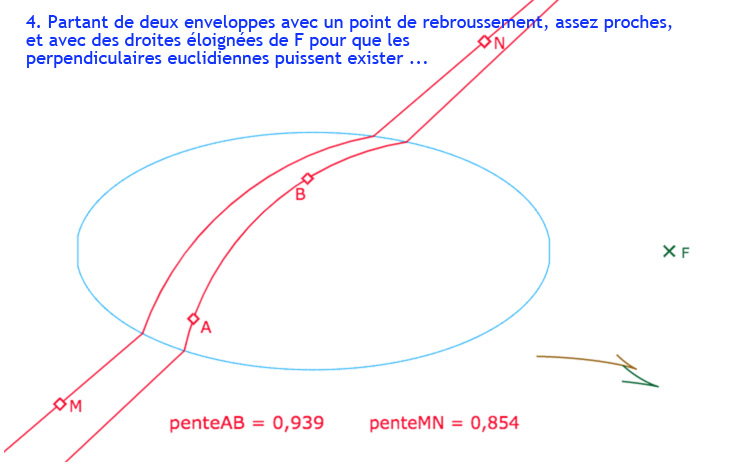
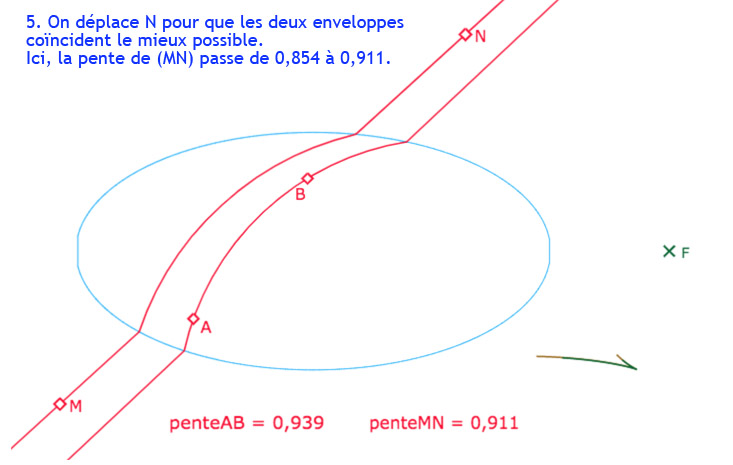
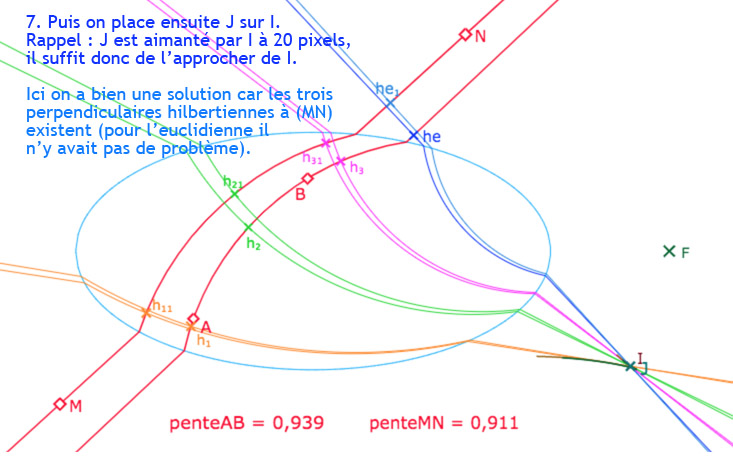
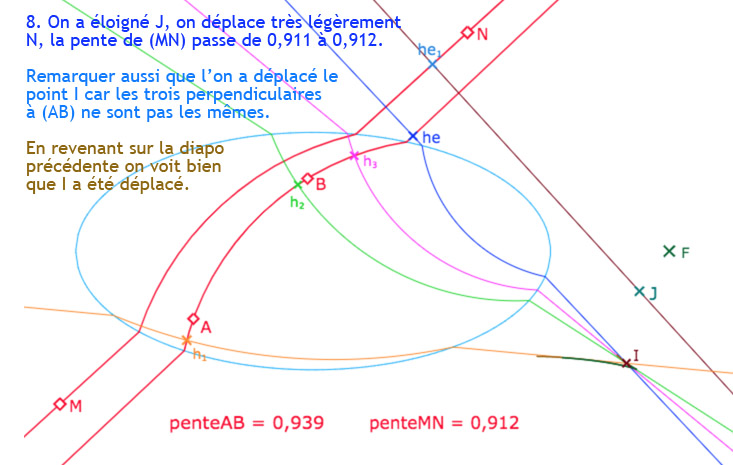
Ayant construit la frontière comme enveloppe d’un point, sous forme de lieu, il est facile, moyennant quelques aménagements pour éviter une construction trop lourde, de la transformer en macro-construction. On dispose donc d’une figure dans laquelle on peut construire les deux enveloppes pour deux droites, la droite \((AB)\) et une droite \((MN)\). On a vu que l’on peut construire trois perpendiculaires hilbertiennes au voisinage interne d’un point de rebroussement, donc on s’intéresse à placer les deux droites pour avoir ces deux points de rebroussements. Ensuite il s’agit de les faire plus ou moins coïncider pour que d’un point commun on puisse avoir deux fois trois perpendiculaires hilbertiennes et une euclidienne.
Principe de manipulation de la figure proposé
Cette galerie de 9 diapo comprend une première partie (de 3 diapos) d’appropriation de la figure, puis un détail de la procédure (4 diapos) et une autre solution (2 diapos)
Figure dynamique associée
Elle comporte un retour à une solution (configuration « initiale »). Il faut donc se placer en mode « Libre » pour pouvoir déplacer les points. C’est le mode à l’ouverture de la figure. Ne pas hésiter de changer la pente de la droite initiale \((AB)\) … ce qui n’a pas été fait dans la galerie précédente.
Attention : ici \(N\) étant dans le widget de commentaires et de commandes, on préfèrera déplacer le point \(M\).
Pour agir directement sur \(N\), il faut déplacer le widget vers le haut car il a priorité sur les points.
On peut aussi s’entrainer en mode « appropriation de la figure » comme au début de la galerie précédente.
Préférer ouvrir cette figure (plus accessibles, plus grande) dans un nouvel onglet.
Régionnement dynamique des parties 2H et 2H1E
L’enveloppe précédente, réalisée sous forme de lieu est désormais transformée en liste de segments. Ce qui permet de construire deux premières parties du régionnement autour de l’orthogonalité – a priori les seules réellement délicates à réaliser – la partie dite 2H, des points d’où il existe deux perpendiculaires hilbertiennes à la droite initiale \((AB)\) et la partie dite 2H1E d’où il existe aussi, en plus de ces deux perpendiculaires hilbertiennes, une perpendiculaire euclidienne.
Exemples de situations rencontrées
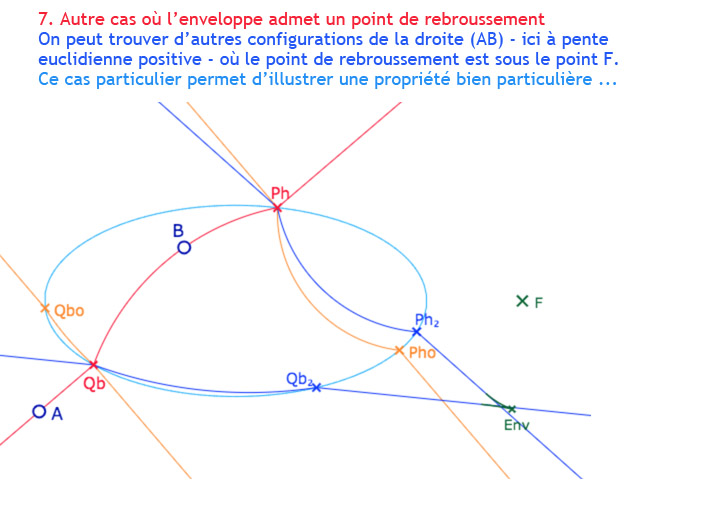
Voici une galerie de 10 illustrations présentant ce que l’on peut explorer avec la figure suivante. On remarquera que l’on a passé du temps à affiner les cas « enveloppe avec point de rebroussement », cette situation étant plus riche que les autres, plus génériques.
Galerie de présentation des situations qui peuvent être explorées avec la figure suivante
La figure dynamique associée
Dans la figure suivante, on peut déplacer les points \(A\) et \(B\) pour modifier la configuration. La droite \((AB)\) doit couper l’ellipse.
Puis déplacer le point \(I\) dans la zone 2H ou 2H1E pour construire les perpendiculaires issues de \(I\) dans ces deux zones.
Gestion dynamique des régions 2H et 2H1E. Agir sur \(A, B, I\). Penser à déplacer l’ellipse.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet
Mise à jour de cette figure en janvier 2025