Rappel de la problématique et des pages précédentes
Étant donnée une droite \((AB)\) qui coupe l’ellipse de Hilbert en deux points \(Ph\) et \(Qb\) et un point \(I\) du plan. Par \(I\) on mène les différente perpendiculaires, hilbertiennes (H) ou euclidienne (E). On sait (construction détaillée dans cette page) qu’il y a 7 cas possibles de construction, le 7° étant le cas où la droite \((AB)\) ne coupe pas l’ellipse n’est pas utilisé ici. On s’intéresse au régionnement du plan, pour le point \(I\), selon le nombre et le type de perpendiculaires à \((AB)\) .
Dans la première page sur le régionnement, on a mis en évidence la spécificité des régions 2H (deux perpendiculaires hilbertiennes) et 2H1E (et une euclidienne), puis on les a construites. La deuxième page a été consacrée à la région 1H1E (une seule hauteur hilbertienne et une euclidienne). Dans cette page, on se propose d’illustrer la réalisation dynamique du régionnement en ajoutant les trois situations manquantes, soit les régions 1E, 1H, et 0P (aucune perpendiculaire).
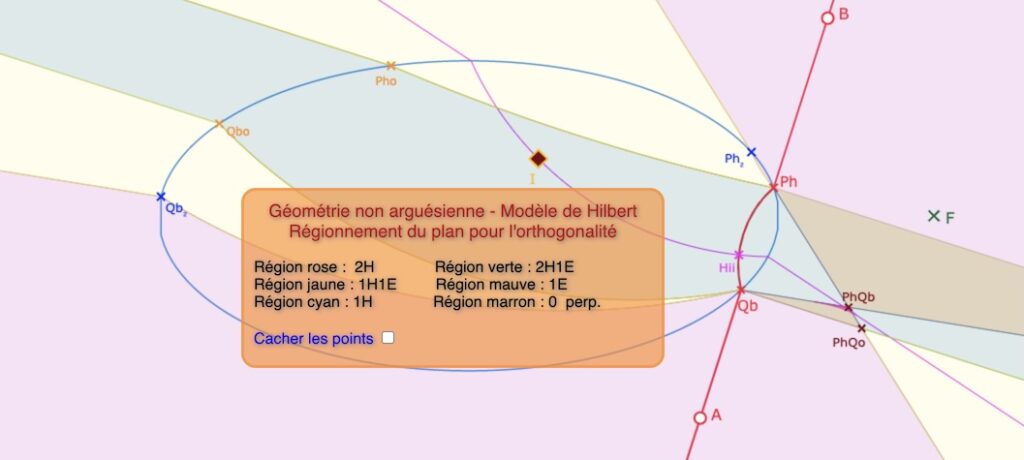
Première illustration du régionnement du plan selon la position de la droite \((AB)\)
On peut déjà remarquer que, quelque soit la position de la droite \((AB)\) par rapport à l’ellipse, il y aura toujours au moins deux parties en mauve (1E) autour des points \(Ph\) et \(Qb\), et que ces parties sont nécessairement non bornées car il suffit d’éloigner le point \(I\) de l’ellipse pour avoir une perpendiculaire euclidienne ordinaire, et rien d’autre.
Dans l’illustration ci-dessus, il y a deux parties 1H (en cyan), et elles sont, ici, elles aussi toutes les deux non bornées, en particulier, pour celle passant par les points \(Ph\) et \(Qb\), parce que les droites \((PhPho)\) et \((QbQbo)\) sont parallèles, comme orthogonales toutes les deux à \((AB)\). Enfin, les deux parties 0P (marron), sans perpendiculaire, sont bornées, l’une étant le triangle \(Qb \, PhQb \, PhQo\) et l’autre le triangle \(Ph \, PhQb \, QbPo\) , ce dernier point, intersection des droites affines \((Qb \, Qb_2)\) et \((Ph \, Pho)\) , étant hors écran. On rappelle à l’occasion, comme on le voit ci-dessus, que \(PhQo\) est l’intersection des droites affines \((Ph \, Ph_2)\) et \((Qb \, Qbo)\). Nous allons voir que la région 1H peut être réduite à une seule partie, bornée, alors que 0P peut avoir, elle aussi, ses parties non bornées.
Une figure dynamique est proposée à la fin de cette page de présentation.
Introduction générique
Dans la première illustration, les deux parties de 1E coupent l’ellipse, mais on peut avoir un contexte où la région 1E ne rencontre l’ellipse uniquement qu’en les deux points \(Ph\) et \(Qb\) comme ci-dessous.

Configuration où chaque région 1E, 1H, 0P est composée de deux parties, et 1H1E de 4 parties.
Voici une configuration « assez proche » de la symétrie par rapport à l’axe focal de l’ellipse, en choisissant la droite \((AB)\) proche de la verticale. La région 1H1E est alors composée de 4 parties, deux issues de \(Ph\) et \(Qb\) et deux de \(PhQo\) et \(QbPo\).
La région 1H est répartie en deux parties non bornées car portées, toutes les deux, par les droites \((Ph \, Pho)\) et \((Qb \, Qbo)\), parallèles comme perpendiculaires à \((AB)\) en \(Ph\) et \(Qb\). L’une de ces parties traverse l’ellipse. En effet, il y a toujours une partie de 1H passant par les points \(Ph\) et \(Qb\) car, entre ces deux points il y a toujours une partie d’où on peut mener une perpendiculaire hilbertienne à \((AB)\) par existence d’un cercle orthogonal à l’arc de la droite \((AB)\) passant par \(F\).
Entre ces différentes parties de 1E et 1H, la région 0P est elle aussi divisée en deux parties autour de \(PhQb\). On notera que les 4 régions 1E1H, 1E, 1H, 0P ont toutes pour sommet les points \(PhQo\) et \(QbPo\). Ce cas va être assez général – les points étant intersection de deux droites – avec la nuance que les points vont être transformés en leurs versions hilbertiennes quand ils seront à l’intérieur de l’ellipse, comme ici :
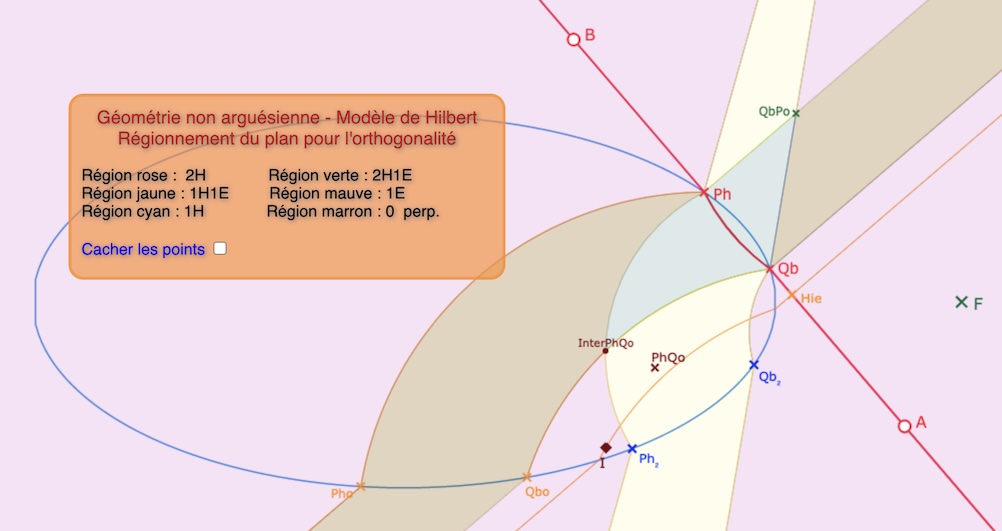
Exemple d’une configuration avec \(PhQo\) intérieur à l’ellipse
Dans cette configuration la région 1E est composée de 4 parties, passant par les 4 sommets précédents, le sommet \(PhQo\) étant transformé en le point \(Inter_{PhQo}\) intersection des droites, non plus affines, mais hilbertiennes \((Ph \, Ph_2)\) et \((Qb \, Qbo)\). La région 0P est composée de deux parties non bornées, car, comme dans le cas 1H de l’illustration précédente, portées à nouveau par les droites \((Ph \, Pho)\) et \((Qb \, Qbo)\). La région 1H semble être réduite à une seule partie, bornée, entre \(QbPo, Ph, Inter_{PhQo}, Qb\). Les droites \((Ph \, Ph_2)\) et \((Qb \, Qb_2)\) se coupent en \(PhQb\). On peut se demander si la partie, hors écran, au dessus de \(PhQb\) peut être une partie de 1H.
Tout d’abord, le franchissement d’une des quatre droites, \((Ph \, Ph_2), \; (Ph \, Pho), \; (Qb \, Qb_2), \; (Qb \, Qbo)\), dites plus loin « droites de base » du régionnement, produit un changement de région. Ainsi la partie au dessus de \(PhQb\) pourrait être de type 1H ou 1H1E. Mais la configuration est telle qu’en s’éloignant de l’ellipse dans les ordonnées, il sera facile d’obtenir une perpendiculaire euclidienne. Donc la partie au dessus de \(PhQb\) dans le prolongement de la partie jaune est encore une partie 1H1E, et donc encore jaune.
En voici une illustration, en dézoomant la figure dans la même configuration

Cette configuration est composée d’une seule partie bornée pour 1H et deux parties non bornées pour 1H1E.
Cas où 1E ne passe pas par un des points de référence
\(PhQb, PhQo, QbPo\)
C’est le cas quand il y a une partie 2H et/ou 2H1E adossée à une partie 1E. Ainsi, ci-dessous, Entre les droites \((Ph \, Ph_2)\) et \((Ph \, Pho)\) il y a une partie 2H1E, verte, précédée d’une partie 2H, rose. La partie 1E commence donc, non pas à partir de \(QbPo\), mais à partir du point de coupe \(eCoup_1\) de \((Ph \, Pho)\) entre les parties 2H et 2H1E.
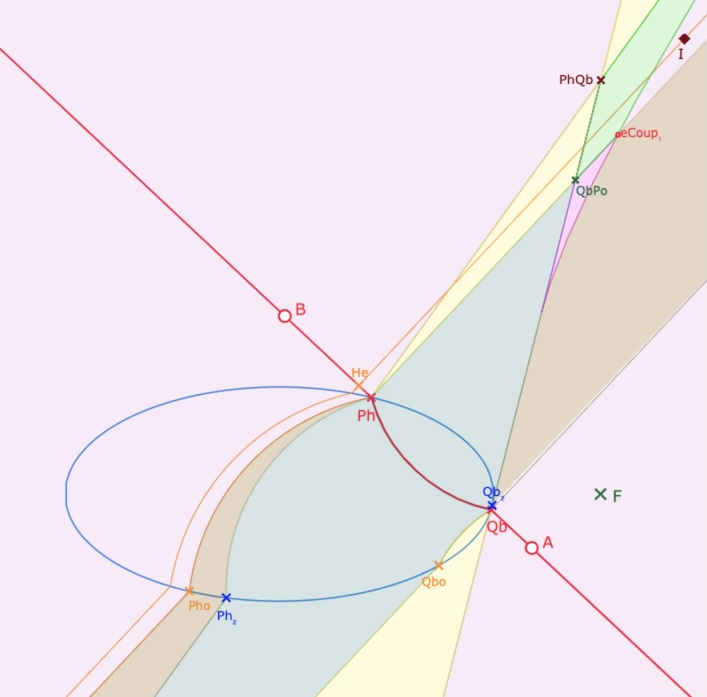
Exemple d’utilisation du point \(eCoup_1\) comme sommet d’une de partie de 1E.
On peut à nouveau se questionner sur le type de la partie, pour les ordonnées négatives, en dessous de l’intersection \(PhQo\) qui serait la pointe inférieure de la partie 1H à l’écran. Entourée des régions 1H1E et 0P elle ne peut être qu’une seconde partie de 1H ou une quatrième partie de 1E.
En dézoomant (très fort) la figure, on voit que c’est une partie 1E, ce qui pourra s’anticiper simplement quand on aura un peu argumenté sur cette question.

Cette configuration n’a aussi qu’une seule partie pour 1H, bornée, et 4 parties pour la région 1E.
Les différentes configurations où \(QbPo\),
ou \(PhQo\) sont à l’intérieur de l’ellipse
On a déjà montré une situation où \(PhQo\) est intérieur à l’ellipse. Ce n’est possible que si la droite \((AB)\) est à pente négative. Dans l’exemple ci-dessus, la droite passait près du sommet proche de \(F\). Toujours avec une droite à pente négative, on peut aussi avoir \(PhQo\) à l’intérieur de l’ellipse si la droite passe près de l’autre sommet de l’ellipse comme ci-dessous :

Autre configuration – droite à pente négative – pour \(PhQo\) à l’intérieur de l’ellipse. Seule la région 1H est bornée
Si la droite \((AB)\) est à pente positive, c’est l’intersection \(QbPo\) qui peut être à l’intérieur de l’ellipse, dans les même conditions de voisinage de chacun des sommets.

Cas où la droite est à pente positive, avec \(QbPo\) intérieur à l’ellipse (1/2)
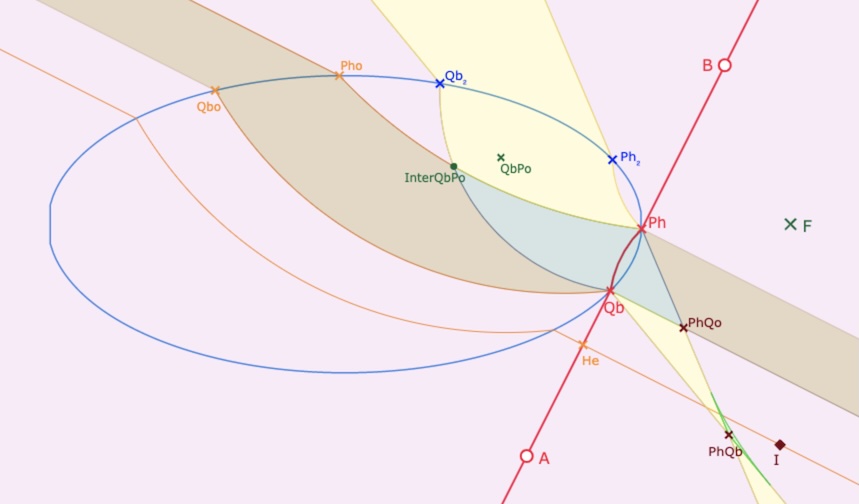
Autre situation avec la droite à pente positive, avec \(QbPo\) intérieur à l’ellipse (2/2)
Dans ces quatre illustrations où interviennent l’un des points \(Inter_{PhQo}\) ou \(Inter_{QbPo}\), on notera que la région 1H est toujours bornée, formée d’une seule partie et que la région 0P est formée de deux parties non bornées car portées par les droite parallèles \((Ph \, Pho)\) et \((Qb \, Qbo)\).
Anticipation du type d’une partie non visibles à l’écran
Comme suggéré ci-dessus il est souvent très simple d’anticiper le type d’une partie non accessible. Voici un exemple choisi aussi pour présenter une partie 2H1E a priori non bornée. On s’intéresse à ce qu’il peut y avoir au dessus de la partie 1H dont la pointe, invisible à l’écran est le point \(PhQo\). La partie en question est entourée de parties 1H1E, 1H et 0P, ne peut être donc être que de type 1E ou 1H. La partie est délimitée par les droites \((Ph_2 \, Ph)\) et \((Qbo \, Qb)\).
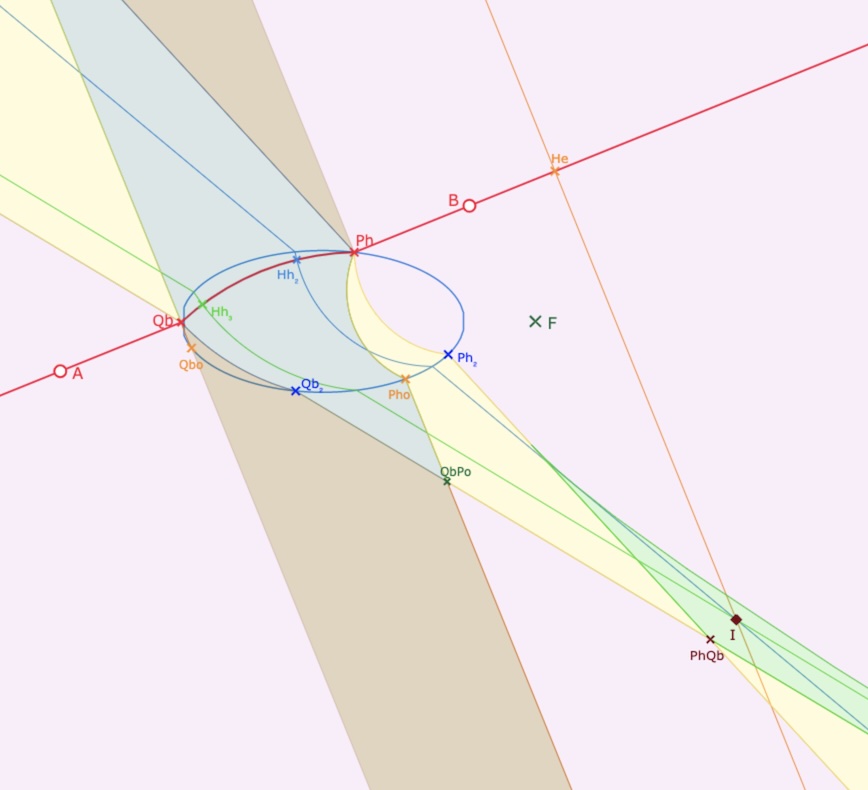
Quel type de région pour la partie au dessus de la partie 1H à l’écran ?
En dézoomant, certes, on voit le résultat, mais argumentons quand même sur la situation. Plaçons le point \(I\) dans la partie jaune au dessus de \(Qb\), et donc à gauche de la droite \((Qb_2 \, Qb)\).

Franchissement par le point \(I\) de la droite \((Ph \, Ph_2)\) (1/2)
En franchissant la droite \((Ph \, Ph_2) = (Ph \, PhQo)\), on reste à gauche de \((Qb_2 \, Qb)\), et donc avec encore une perpendiculaire euclidienne issue de \(I\), il y a donc une composante 1E, la partie ne peut pas être 1H, c’est donc 1E. Par ailleurs, \(I\) franchissant la droite \((Ph \, PhQo)\), la hauteur, \((I \, Hh_1)\) ne peux plus exister – dynamiquement, c’est comme si le point \(Hh_1\) devait sortir de l’ellipse. On ne peut donc être dans une composante 1H.
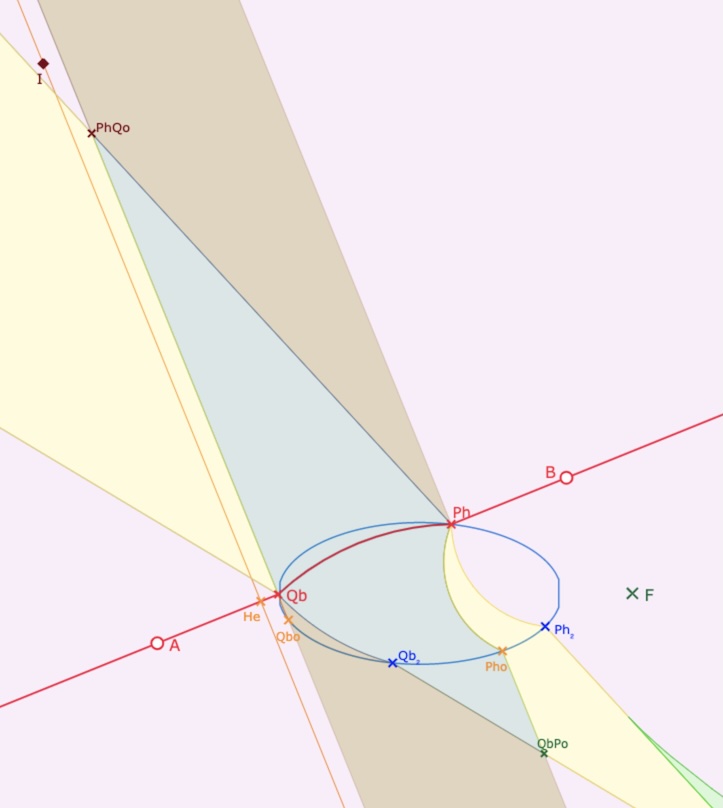
Franchissement par le point \(I\) de la droite \((Ph \, Ph_2)\) (2/2)
Plus précisément, dans les illustrations précédents, on voit que le changement de type au sommet d’une partie 1H n’a lieu que si cette extrémité est l’un des points \(QbPo\) ou \(PhQo\) alors que le type 1H est conservé quand l’extrémité est le point \(PhQb\) comme on peut le voir dans la seconde illustration de cette page. La différence de comportement vient de ce que les deux premiers points sont les intersections de deux perpendiculaires à \((AB)\) de type différent, une hilbertienne, une euclidienne alors que \(PhQb\) est l’intersection des deux perpendiculaires hilbertiennes. Bien entendu, il n’y a pas de point \(PoQo\) car les droites \((Pb \, Pho)\) et \((Qb \, Qbo)\) sont parallèles.
Transformation dynamique de type de région d’une partie du plan
Une situation intéressante à observer est quand deux de ces trois points sont des sommets d’une partie du plan délimité par les droites de base du régionnement : selon que le sommet commun entre cette partie et la partie 1H de référence est \(PhQb\) ou un des deux autres, la partie étudiée est de type 1H ou 1E. Et on passe d’une situation à l’autre en déplaçant un des deux points \(A\) ou \(B\).
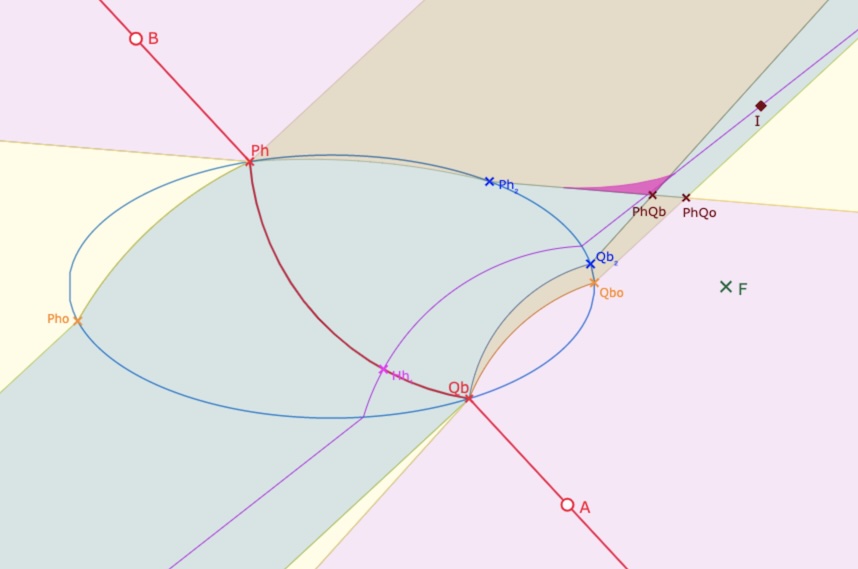
Droite à pente négative – Partie délimitée par les sommets \(PhQb\) et \(PhQo\) avec
en sommet commun, en haut \(PhQb\) (types 1H -1H), en bas \(PhQo\) (types 1H –1E)

Avec une pente positive c’est plus souvent \(QbPo\) qui intervient. On passe d’une illustration à l’autre en déplaçant \(A\) de quelques pixels.
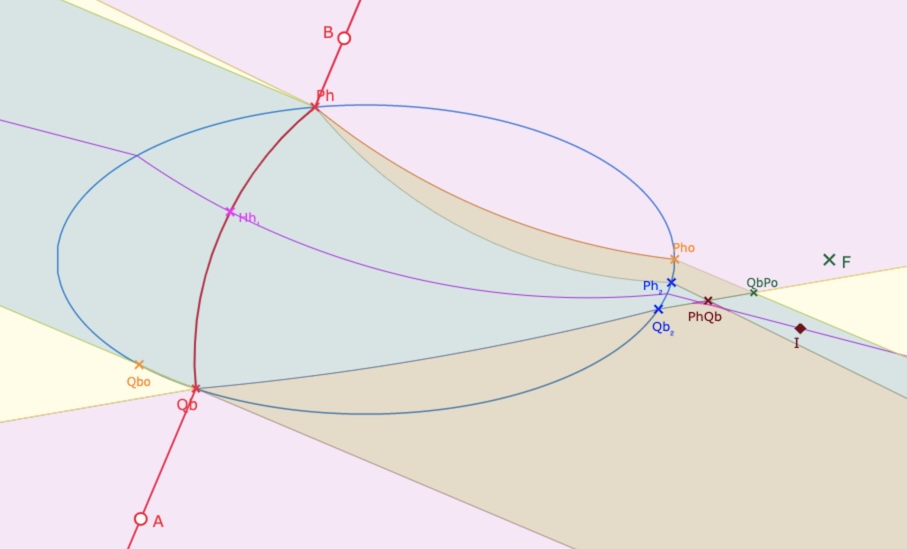
On notera aussi que (abstraction faite des ajouts éventuels de 2H ou 2H1E), deux parties
opposées par \(PhQb\) sont toujours de même type (ci dessus 0P et 1H, ci dessous 1E et 1H1E)

Autour du point de rebroussement des régions 2H et 2H1E
Par simplification d’écriture, on a choisi, quand ces régions ont un point de rebroussement, de ne pas « détourer » cette région par rapport aux autres (ci-dessous 0P et 1H), mais simplement de renforcer l’opacité de cette région 2H ou 2H1E avec le point de rebroussement. Comme on l’a déjà dit dans les pages précédentes, on sait – pour le moment de manière empirique – qu’au voisinage du point de rebroussement, il peut y avoir 3 perpendiculaires hilbertiennes (cas 2H), et, dans le cas 2H1E, il y a une euclidienne en plus. En voici quelques exemples.

Cas du point de rebroussement d’une partie 3H, et donc 4 perpendiculaires issues de \(I\), dans une partie de 1H1E.
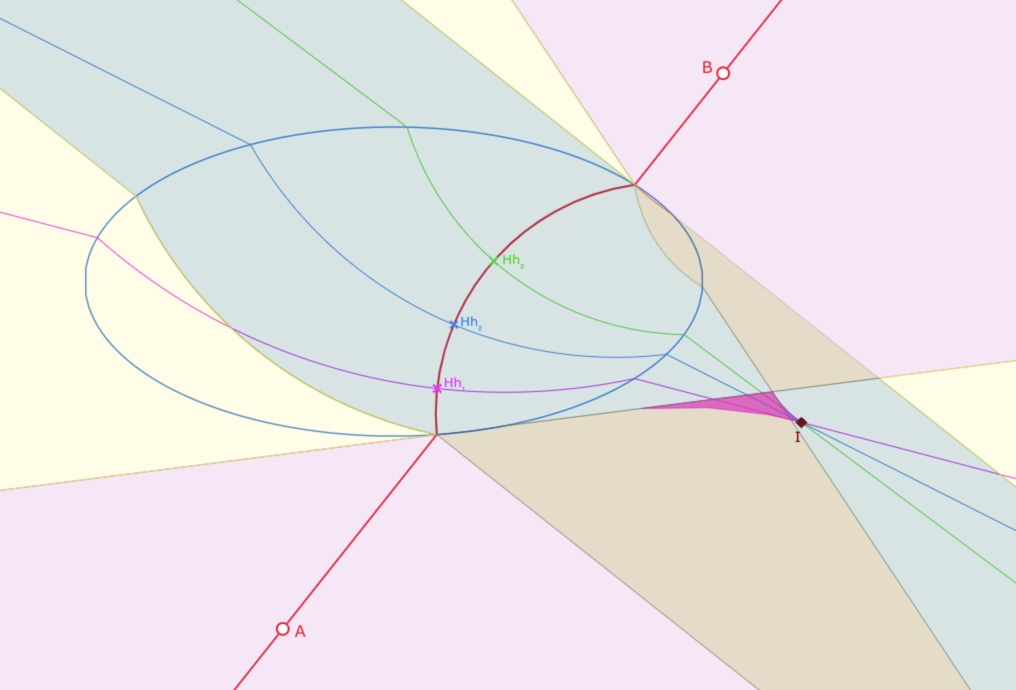
Cas de pointe rose dans une partie de la région 1H.
Deux des perpendiculaires hilbertiennes peuvent être confondues
La mise en évidence graphique d’une racine double – qui existe probablement assez souvent – n’est pas évidente à réaliser. On choisit une partie 2H sous forme de grande flèche. On affiche la distance (euclidienne) entre les deux pieds des perpendiculaires \(Hh_2\) et \(Hh_3\) avec la précision maximale de DGPad, soit 13 décimales.

Ci-dessus, présentation de la figure, avec deux pieds \(Hh_2\) et \(Hh_3\) distincts.
Ci-dessous, on place le point \(I\) à la pointe de la zone, la distance devient nulle (à la précision \(10^{-13}\)).
On a ajouté l’affichage des deux arcs (visible dans la levée de l’ambiguité).

Un autre exemple très particulier
On peut rencontrer des situations nettement plus surprenantes. Dans l’illustration suivante on a laissé apparaitre quelques variables de la figure :
• expFrVerte non vide signifie qu’il y a une partie verte, de frontière – Fr dans le nom – à 11 éléments donc assez longue.
• p2H1Esup=0 signifie que cette partie (2H1E) est sous les droites se coupant en \(PhQb\)
• PtReb=1 signifie qu’il y a un point de rebroussement
• MaxPtInd donne les coordonnées de ce point de rebroussement et son index dans la liste expFrVerte.
• Amplitude indique la distance maximale entre les points consécutifs de la liste expFrVerte, bien trop faible ici (environ 3 pixels) pour qu’elle soit vraiment visible, même si on distingue un peu de vert autour du point \(PhQb\).
Autrement dit, dans dans cette configuration, il y a un point de rebroussement et donc potentiellement une possibilité de quatre perpendiculaires en un point \(I\) bien placé, la quatrième, euclidienne, étant assurée car le point \(PhQb\) est entourée des régions 1E et 1H1E.

Point de rebroussement invisible : analyse de la situation par les variables de la figure :
mise en évidence d’un point de rebroussement invisible.
En utilisant l’outil aimantation du logiciel sur le point \(I\) par le point de rebroussement, on arrive effectivement à cette situation :

Accès à un point de rebroussement, prévu par les calculs de la figure, mais invisible à l’œil.
Confirmation par les quatre perpendiculaires à \((AB)\) issues de \(I\).
Droite \((AB)\) de pente proche de 0
A priori, la construction de la figure étant basée sur différentes données numériques, dont la pente de la droite \((AB)\). Et donc, avec lla figure proposée en fin de page,, il n’est pas possible que la droite soit verticale. Mais on peut l’approcher comme dans ces deux illustrations.
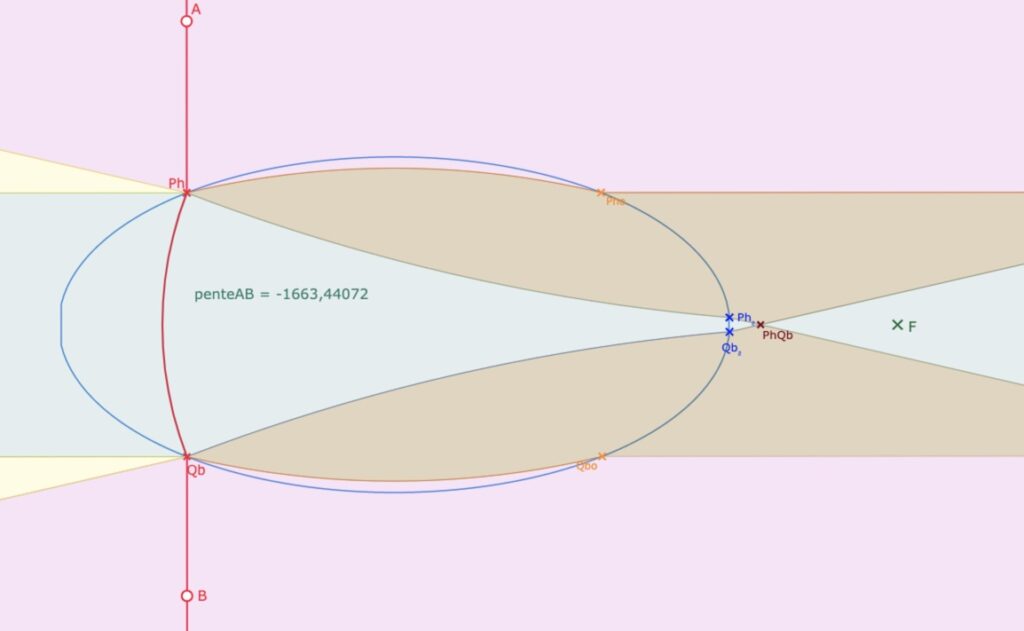
Ci dessus pente négative de – 1663 ; ci dessous pente positive de 1055

On évitera aussi la droite effectivement de pente nulle. Par contre, on peut approcher de très près l’horizontalité de la droite \((AB)\). Sans entrer dans les détails techniques (un article de blog y sera consacré ultérieurement), un autre critère significatif est le signe, autour de \(Ph\), de \(x(Pho)-x(Ph)\) (noté dans le code JavaScript \(Pho[0]-Ph[0]\) ), et, autour de \(Qb\), celui de \(x(Qbo)-x(Qb)\) (noté encore \(Qbo[0]-Qb[0]\) ). Il y a alors deux situations, selon la position de la droite par rapport au point \(F\) à cause de la partie de la droite \((AB)\) à l’intérieur de l’ellipse qui est l’arc de cercle passant par \(Ph, \, Qb\) et \(F\).
Si la droite \((AB)\) est au dessus de \(F\)
Si ces critères \(x(Pho)<x(Ph)\) et \(x(Qbo)<x(Qb)\) sont en général pertinents, la question se pose quand même quand la droite est quasi horizontale car le signe pourrait ne pas être stable, les droites \((Pho \,Ph)\) et \((Qbo \,Qb)\) étant alors quasi verticales. Même s’il y a un traitement particulier à réaliser, la situation ne pose pas de problème spécifique, les différences étudiées restent du même signe que la pente.
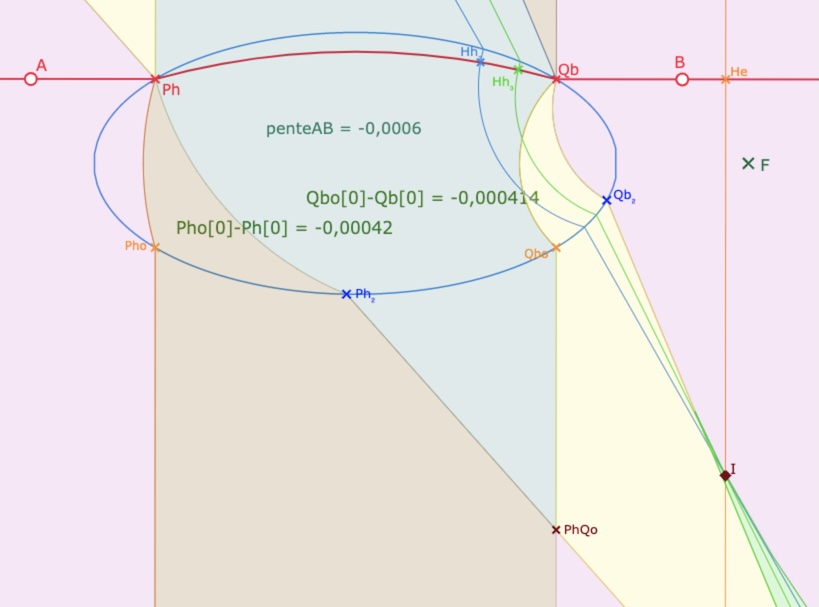
Ci-dessus la droite est à pente négative, ci-dessous, à pente positive
Dans les deux cas, \(x(Pho)-x(Ph)\) et \(x(Qbo)-x(Qb)\) sont du même signe que la pente de la droite.
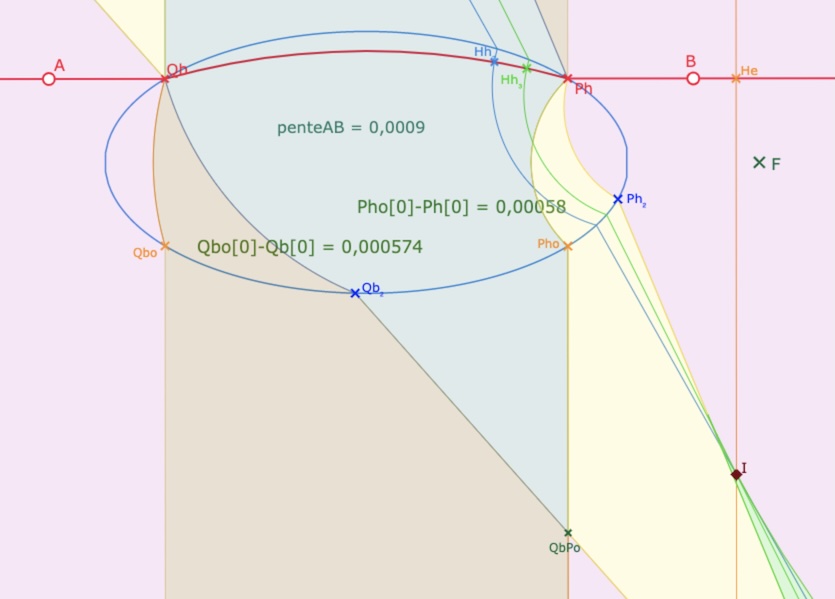
Si la droite \((AB)\) est en dessous de \(F\)
Dans le cas où la droite est sous le point \(F\) le signe des différences est encore constant mais c’est l’opposé de celui de la pente, ce qui somme toute, dans les deux cas, est tout à fait logique.
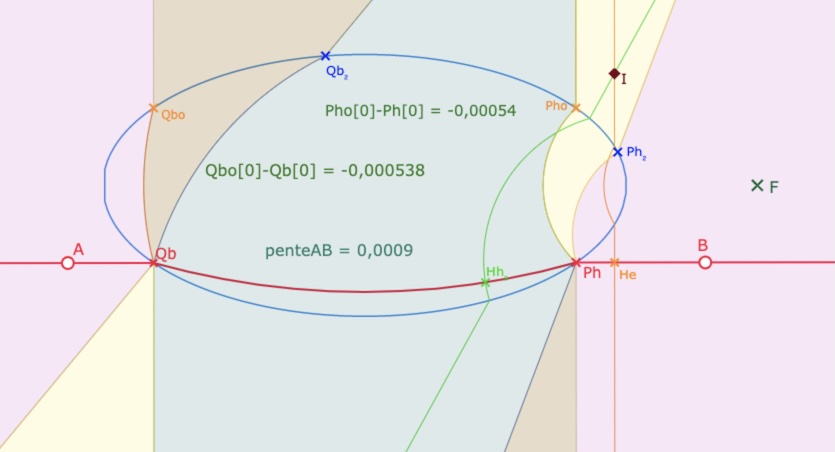
Cette fois-ci, \(x(Pho)-x(Ph)\) et \(x(Qbo)-x(Qb)\) sont du signe opposé à celui de la pente de la droite.
Ci-dessus avec une pente de la droite positive, ci-dessous, pente négative, \(I\) dans la partie verte quand elle existe.

Illustrations de cas où la droite est aussi très proche des sommets non focaux de l’ellipse
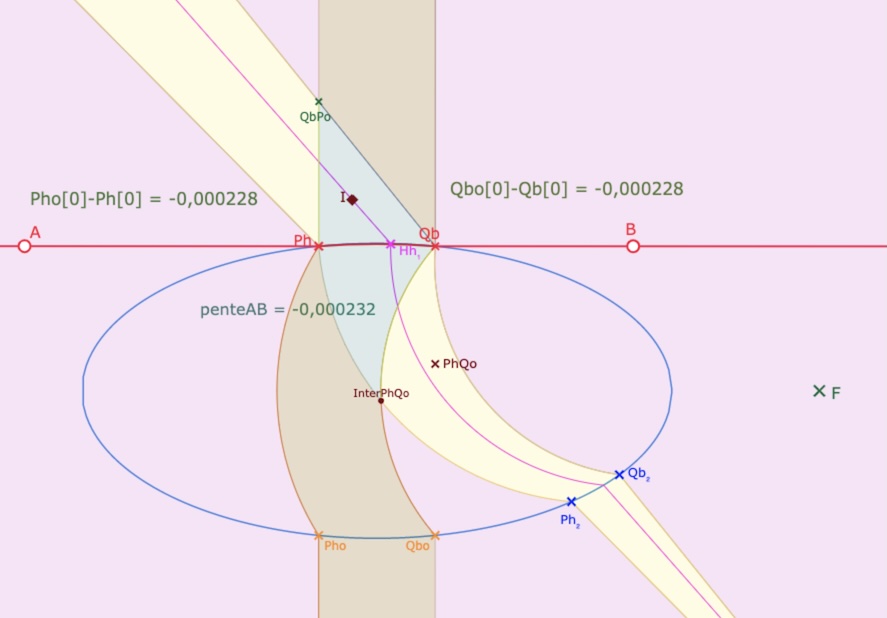
Dans ces deux cas avec une pente négative (\(PhQo\) dans l’ellipse), en valeur absolue, de l’ordre de 0,0002.
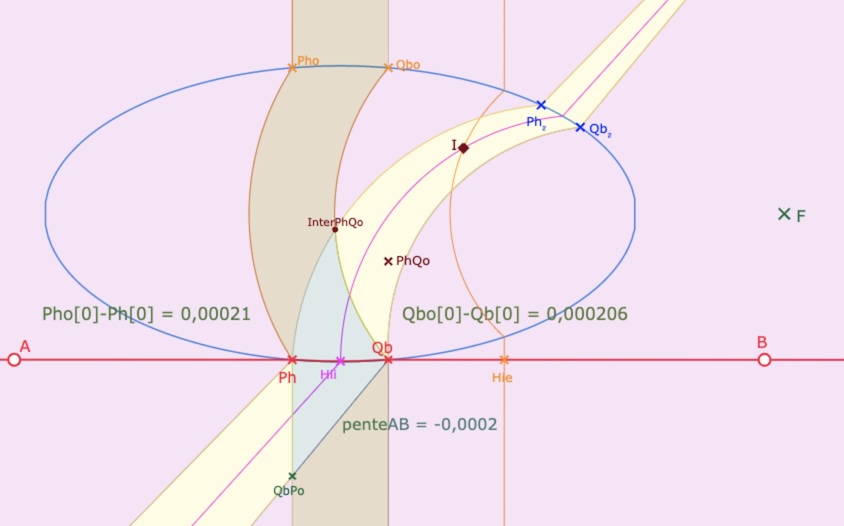
Et des pentes positives, en valeur absolue encore plus faibles que les précédentes
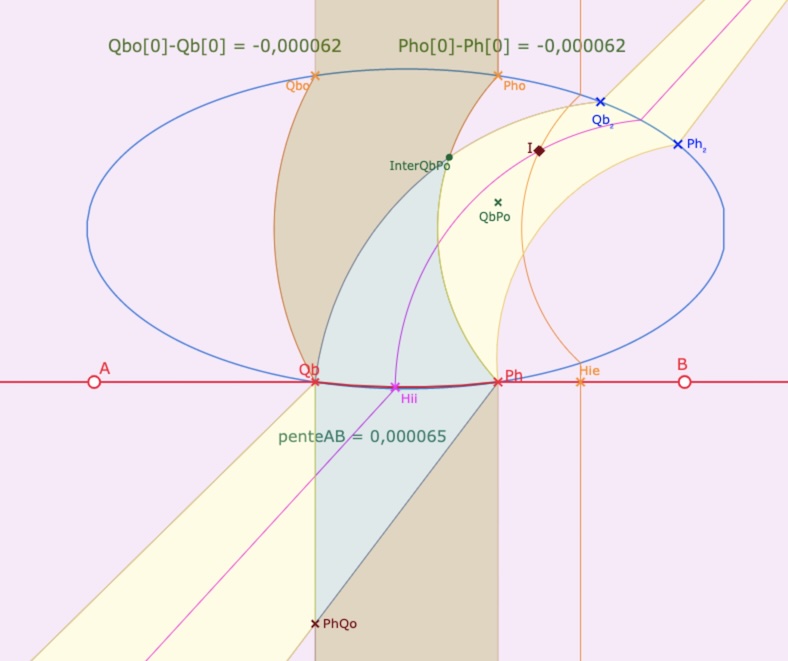
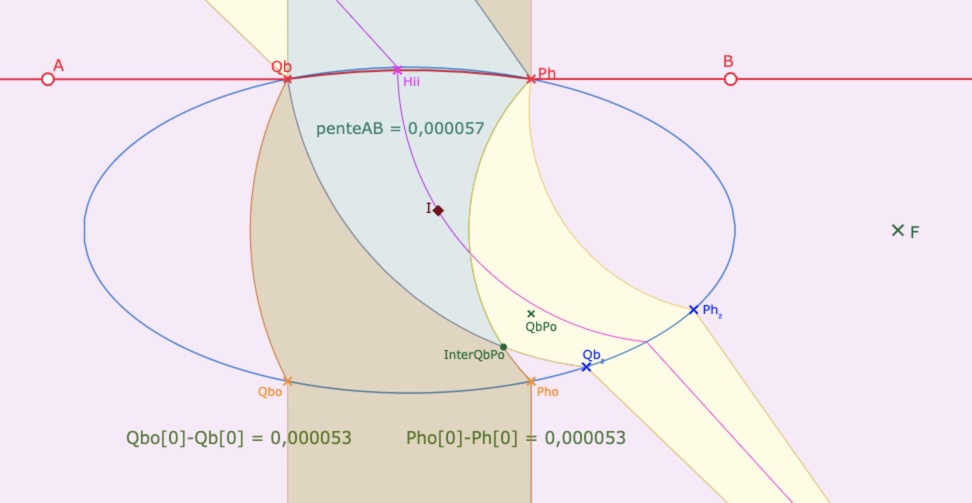
Ici avec une pente positive (\(QbPo\) dans l’ellipse), de l’ordre de 0,00006.
La figure dynamique (de travail)
Cette figure n’est pas encore complètement exempte de problèmes mais elle est déjà largement utilisable. Elle comporte encore quelques bug inhérent à la façon un peu trop rapide d’avoir traité la frontière 2H et 2H1E qui est limitée à une liste de 16 segments. Il peut y a avoir des bugs autour de ce traitement. En particulier les deux parties marrons, un peu symétriques, bornées peuvent disparaître toutes les deux (alors qu’elle sont construites).
Un autre bug apparaît parfois sur les parties 2H et 2H1E, (rarement mais cela peut arriver) une partie clairement 2H s’affiche en 2H1E (une partie verte devrait être rose). En fait cette situation a été la première à avoir été abordée, je ne le ferais plus de la même façon maintenant, cela sera donc refait, éventuellement avec une approche algébrique comme le reste de la figure.
Les autres bug possibles sont des situations élémentaires à corriger, qui vient du changement de signe des pentes des 4 droites de référence. J’ai fait la correction sur plusieurs dizaines de situations mais possiblement pas toutes.
Tout d’abord déplacer le point \(I\) pour le mettre dans les différentes régions.
Penser à déplacer le commentaire, ou l’ellipse à la souris On peut aussi dézoomer (un peu).
Éviter de zoomer : d’une manière générale, la figure n’est correcte que si l’ellipse entière est à l’écran.
On peut ouvrir cette figure dans une nouvelle page (plus grande, plus manipulable – MaJ 7 juillet 25)