On aborde désormais la programmation avec Blockly
L’auto-référence des objets
L’auto-référence des points ou des expressions dans un logiciel de géométrie dynamique n’est pas une nouveauté, c’est une propriété qui est déjà présente dans CaR (Compas and Rulers) le logiciel de René Grothmann, moteur original de CaRMetal. C’est donc, par héritage, une propriété de CaRMetal que nous avons déjà plusieurs fois exposé sur le site de l’IREM de La Réunion ou dans certains anciens articles de MathémaTICE, articles désormais obsolètes car illustrés dans un environnement Java. L’auteur de CaRMetal a voulu faire, sur ce point aussi, mieux – bien mieux – avec DGPad.
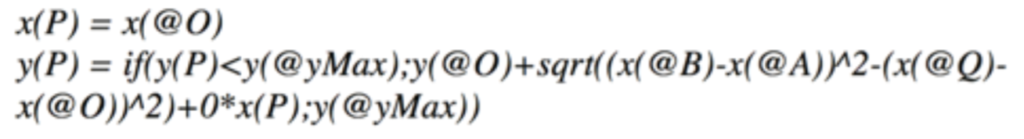
En effet si la mise en oeuvre était assez ésotérique avec CaRMetal (ci-contre de l’auto-référence croisée des points P et Q), elle va devenir complètement transparente avec Blockly dans DGPad.
On peut simplement explorer les figures suivantes sans s’intéresser vraiment au code nécessaire pour produire ces figures. Le code est donné pour les personnes intéressées par ces questions.
Rupture du déterminisme : la mémoire de l’action
Exemple symbolique du thermomètre à mémoire
L’exemple introductif est toujours le même, car c’est l’archétype de la rupture conceptuelle qu’il procure dans la géométrie dynamique. On s’offre ici un thermomètre horizontal.
On se donne une droite parallèle à l’axe des abscisses, et un point M sur cette droite. On se propose de construire deux points Min et Max qui sont les « curseurs-mémoire » des positions minimales et maximales de M quand l’utilisateur déplace M sur la droite. Si on arrive à construire ces deux points, on est dans la brisure du déterminisme, car en remettant M à la position initiale on veut que ces deux points restent à leur place, et donc gardent une trace de l’histoire de la manipulation.
D’une certaine façon, de manière simplifiée, on insère le temps de l’utilisateur dans la figure (le concept de temps mais pas sa mesure). Or, l’implémentation de Blockly dans DGPad permet de faire cela tout simplement.
Rompre et rétablir le déterminisme
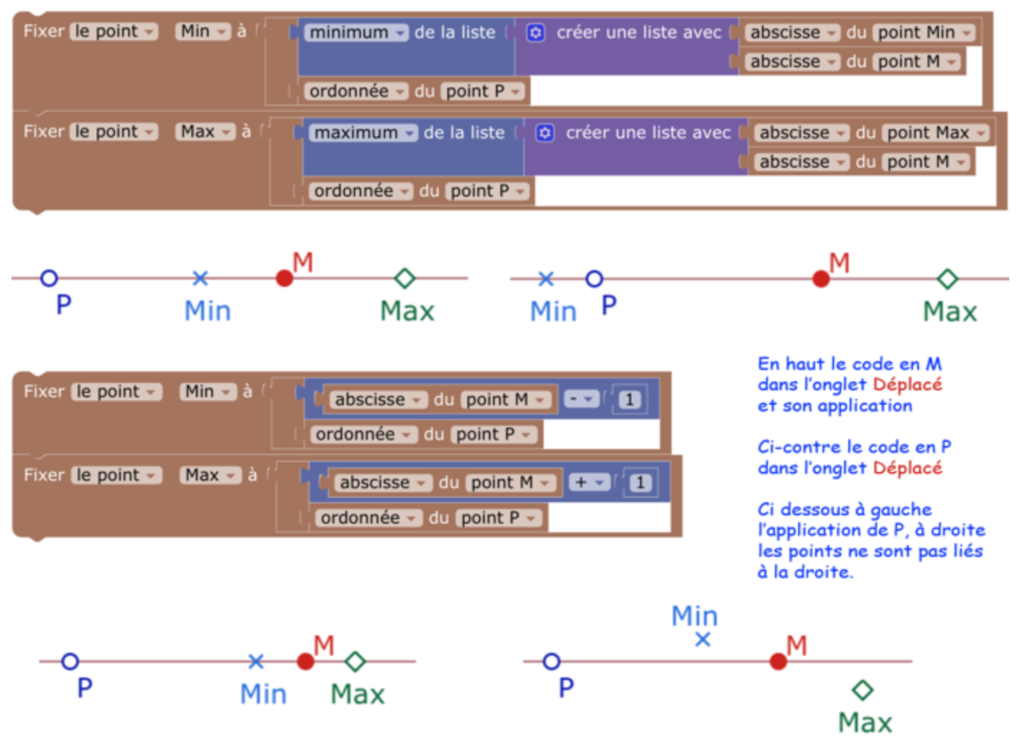
Le code en M a du sens car Blockly permet l’auto-référence : Min est défini à partir de Min.
On observera que, dans ce contexte, l’initialisation de cette démarche récursive
est l’existence du point : le fait de créer un point Min l’initialise.
Le point M est un point sur objet de la droite parallèle à (Ox) – l’axe – passant par un point P.
On réinitialise le processus dans le déplacement du point P qui replace Min et Max à ce que l’on peut appeler les conditions initiales. Et donc, si on brise le déterminisme, on sait aussi construire les outils qui permettent de le rétablir.
Techniquement on remarque qu’ici les coordonnées de Min et Max sont déterminées dans des blocs de comportement de M, et la réinitialisation dans des blocs de P. Avec CaRMetal, les codes étaient nécessairement dans les coordonnées des points Min et Max eux-mêmes.
Déplacer M à gauche et à droite pour voir que les « curseurs » Min et Max restent à leur place. Réinitialiser en déplaçant P.
Une utilisation didactique immédiate du « thermomètre à mémoire »
Dans la figure suivante, on applique cette technique pour faire prendre conscience, kinesthésiquement, avec le doigt (si on est sur une tablette ou un téléphone), que le sens de variation d’une fonction sur un intervalle est un concept global alors que souvent les élèves en font, en acte, un concept local, limité aux extrémités de l’intervalle étudié.
L’expérience utilisateur de la tablette a une dimension tactile parfois d’une grande pertinence, pour aborder autrement certains concepts. Ici la figure est construite sur la nécessité de parcourir tout un intervalle pour voir se construire – temporellement – les extrema de la fonction : la rupture du déterminisme devient un outil au service de l’apprentissage d’une dimension nouvelle et difficile du champ fonctionnel : la globalité d’un concept (alors que l’algèbre est plus sur la localité). Le fait de le faire sur tablette (en classe de seconde) s’est montré plus prégnant que sur ordinateur, à cause du contact direct probablement.
Conceptuellement, déplacer M est dans la rupture du déterminisme alors que déplacer un des points A, B C ou D le rétablit.
Référence croisée de points
Le comportement souple de Blockly sur les points permet d’aller plus loin non seulement techniquement, mais aussi didactiquement, pour proposer des modélisations au plus près des définitions. C’est le cas des points symétriques : deux points sont symétriques par rapport à un point I si I est leur milieu (définition du programme de 5°). Rendre compte de cette définition en géométrie dynamique serait de réaliser une figure où un point ne serait pas privilégier par rapport à un autre, et donc que si A et B sont symétriques par rapport à I il faudrait que l’on puisse agir sur les point A, I mais aussi B.
C’est ce que nous allons réaliser avec Blockly, le plus simplement possible : juste en l’écrivant. C’est l’implémentation de Blockly qui fait ce que l’on attend, en toute transparence. On considère deux cercles, de rayon fixe, de centres M et N symétriques par rapport à I. On place A et B sur chacun des deux cercles, eux aussi symétriques par rapport à I. Tous ces points sont en manipulation directe.
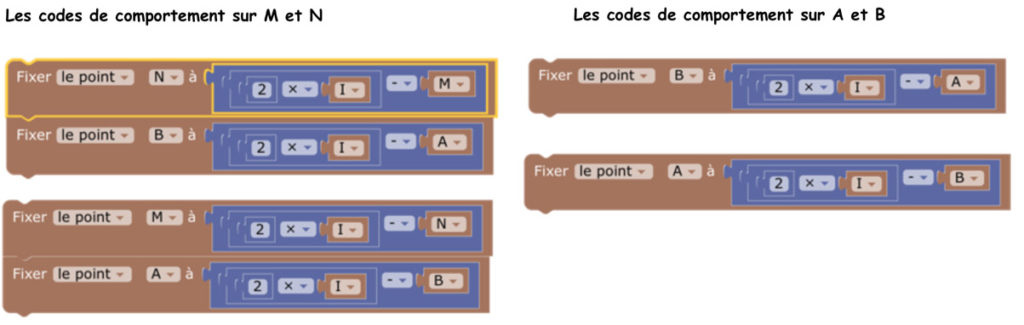
Mais comment est-ce possible ? Pourquoi A et B restent sur les cercles quand on les prend en main ?
C’est la seule question à se poser. La réponse est toute simple, mais un peu subtile : il y a un mélange de type. A et B sont aussi aimantés à 5000 pixels (soit très fortement) aux cercles ; donc ils restent sur les cercles.

On le voit dans le code du fichier ci-contre, mg étant le codage interne du magnétisme : A et B sont aussi aimantés aux cercles et le comportement de Blockly n’annule pas ce typage particulier.
Extension de virtualisation des définitions
Dans la figure suivante on étend le principe de référence croisée à la référence croisée multiple. On a construit un carré ABCD de centre O, construction pour laquelle on peut déplacer A mais aussi B, C ou D, et même O. Le carré est donc de centre O passant par A, mais aussi de centre O passant par B, par C ou par D. C’est un autre type de carré… et l’on comprend qu’il devient plus délicat de définir ce que sont ces objets qui ne sont plus seulement mathématiques mais aussi, de fait, informatiques.
On peut déplacer tous les points de la figure. C’est un peu moins stable quand on déplace O
car il faut garder trace de la translation pendant qu’on l’effectue.