Cas où un seul sommet est à l’intérieur de l’ellipse
Constructions de triangles de somme d’angles égale à 180°
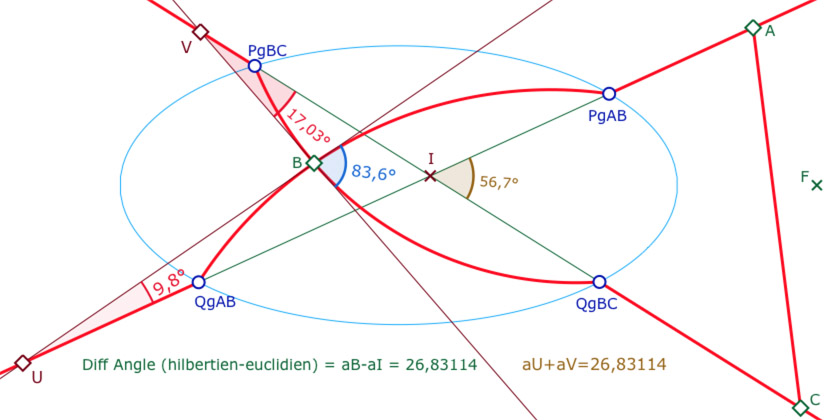
Comme dans la page précédente, on construit les deux H-droites passant par le sommet intérieur à l’ellipse, le point \(B\), à partir des points d’intersection de ces droites sur l’ellipse, en les nommant \(Pg_{AB}, Qg_{AB}, Pg_{BC}, Qg_{BC}\), comme dans les figures du cas général. On construit ainsi les H-droites \((Pg_{AB}\; Qg_{AB})\) et \((Pg_{BC}\; Qg_{BC})\) sur lesquelles on place, respectivement, les points \(A\) et \(C\), à l’extérieur de l’ellipse, plus précisément sur des demi-droites précises comme illustré ci-contre.
Les droites euclidiennes \((Pg_{AB}\; Qg_{AB})\) et \((Pg_{BC}\; Qg_{BC})\) se coupent en \(I\).
La différence de la somme des angles entre le triangle de Hilbert \(ABC\) et le triangle euclidien \(ABC\) est égale à la différence des angles en \(B\), sommet hilbertien, et \(I\), sommet euclidien. On nomme \(U\) l’intersection de la tangente en \(B\) à la H-droite \((Pg_{AB}\; Qg_{AB})\) et de sa version euclidienne, et \(V\) celle de la tangente en \(B\) à la H-droite \((Pg_{BC}\; Qg_{BC})\) et de son pendant euclidien.
Alors, par un calcul immédiat d’angles dans les triangles euclidiens \(UBV\) et \(UIV\) , la différence angulaire – pour cette configuration d’un arc concave et d’un arc convexe – est égale à la somme des angles \(\angle BUI + \angle IVB\), nommée \(aU+aV\) ci-dessus. Ce serait la même chose avec un triangle construit à partir des angles supplémentaires en \(B\) et en \(I\) – et en plaçant \(A\), cette fois, sur la demi-droite euclidienne \([QgAB \; U)\).
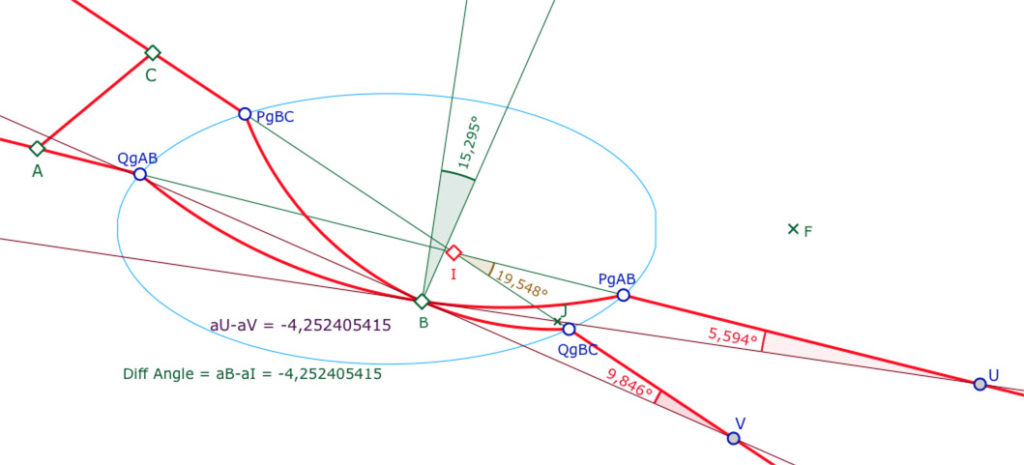
En fait cette somme \(aU+aV\) est algébrique. Si les arcs de cercles intérieurs à l’ellipse sont de même type (concaves ou convexes), l’angle en \(B\) peut être aussi mesuré comme l’angle en \(B\) avec les centres des arcs de cercles.
En conservant les angles géométriques, dans les triangles \(BJV\) et \(IJU\) , on a l’égalité \(aB+aV=aI+aU\) et donc cette nouvelle différence d’angle \(aB-aI=aU-aV\).

La somme des angle du H-triangle \(ABC\) sera égale deux droits, comme pour le triangle euclidien \(AIC\) ssi \(aU=aV\). Cette égalité, elle, est équivalente à dire que les quatre points \(U, V, B, I\) sont cocycliques.
On veux donc réaliser une figure comme ci-contre. En pratique, on ne cherche pas une construction géométrique exacte, on va plutôt s’intéresse une construction par programmation, approximative mais bien entendu très précise.
Dans la figure proposée ci-dessous à manipulation, \(B\) est à l’origine sur un arc de cercle. Puis on modifie à la marge ce positionnement sur l’arc de cercle pour que le point \(I\) soit sur le cercle circonscrit à \(U, V\) et \(B\).
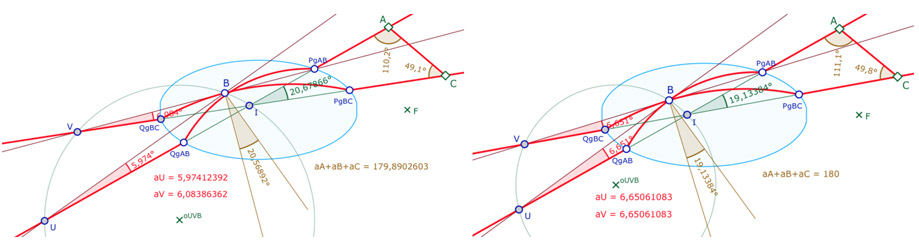
• à gauche, \(I\) est à l’intérieur du cercle circonscrit à \(U, V, B\), la somme des angles est inférieure à deux droits.
• à droite, on a appliqué le code ci-dessous, les angles \(aU\) et \(aV\) sont égaux (à l’approximation du logiciel) et \(I\) est sur le cercle,toujours à l’approximation du logiciel. La précision angulaire est inférieure à \(4.10^{-12}\) degré.

Le point \(B\) est calculé pour être sur l’arc de cercle de la H-droite \((AB)\). Si, comme on l’a plusieurs fois utilisé, Blockly permet de modifier le «comportement» des points sur lesquels il agit, cela signifie aussi que \(B\) devient un point libre en lançant ce code.
Figure dynamique associée
Mode d’emploi
• On peut agir (un peu) sur les points de base\(PgAB, \; QgAB\) et \(B\) sur l’arc (avant de lancer le programme pour \(B\)) ou le point \(PgBC\) en gardant les deux arcs convexes.
• De préférence, lancer le code quand la somme des angles est inférieure à deux droits.
• Il est intéressant de déplacer (légèrement) les points de base sur l’ellipse une fois le code engagé, toujours en respectant la convexité des arcs.
• Recharger la figure avec l’icone de l’iframe redonne à \(B\) son statut de point sur arc.
Manipuler cette figure hors du contexte iframe responsive dans un nouvel onglet.
Autre cas particulier permettant d’obtenir la somme des angles égale à 180°
Il y a une autre façon de réaliser un H-triangle avec un sommet à l’intérieur de l’ellipse et de somme des angles égale à la somme euclidienne. C’est un cas encore plus particulier, celui où les deux angles \(aU\) et \(aV\) sont tous les deux nuls. C’est un cas particulier où la démarche précédente ne s’applique pas (il n’y a pas de cocyclicité), il faut donc réaliser la figure autrement.
De \(aV=0\), on en déduit que la tangente en \(B\) à la H-droite \((BC)\) est parallèle à la droite euclidienne \((PgBC \; QgBC)\) et donc que \(B\) est au milieu de d’arc. Il en est de même, avec \(aU=0\), pour l’arc de la H-droite \((AB)\) et la droite euclidienne \((PgAB \; QgAB)\). Bien entendu il en résulte que \(aB=aI\). On peut alors proposer la figure suivante :
On commence par construire la H-droite \((BC)\) à partir des deux poignées \(PgBC\) et \(QgBC\). \(B\) est nécessairement le milieu de l’arc (pour que \(aV=0\) il faut que la tangente à la H-droite soit parallèle à la corde associée \([PgBC \; QgBC]\)).
Puis à partir du point \(PgAB\) de l’ellipse, on construit l’autre extrémité \(QgAB\) de l’arc intérieur à l’ellipse. On termine cette première étape de la figure par la perpendiculaire au rayon euclidien \([Bo_{AB}]\) en\(B\).
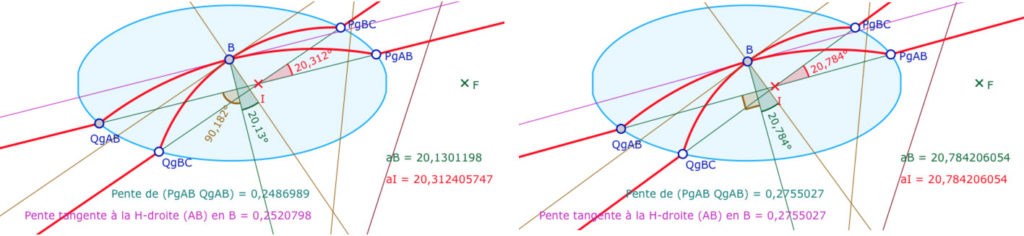
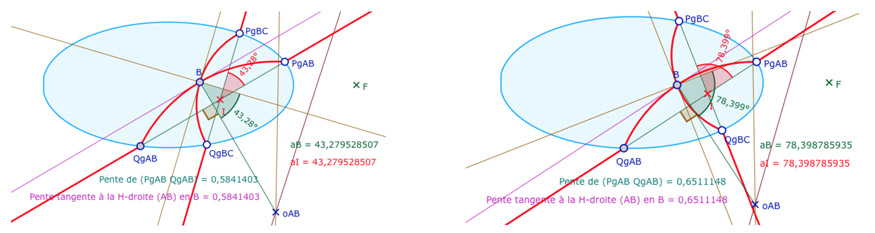
Avec les trois points de base \(PgBC\), \(QgBC\) et \(PgAB\), les angles \(aB\) et \(aI\) ne sont généralement pas égaux et la tangente en \(B\) à la H-droite \((AB)\) n’est pas parallèle à la droite euclidienne \((PgAB \; QgAB)\) comme on le voit dans l’illustration de gauche avec la marque de l’angle marron proche de 90° et les pentes des deux droites.
On choisit alors d’ajuster \(QgBC\) pour obtenir les angles égaux (ci-dessus à droite). La marque de l’angle droit, produite par le logiciel, valide que \((PgAB \; QgAB)\) et la tangente en \(B\) associée sont bien parallèles, à la précision du logiciel.
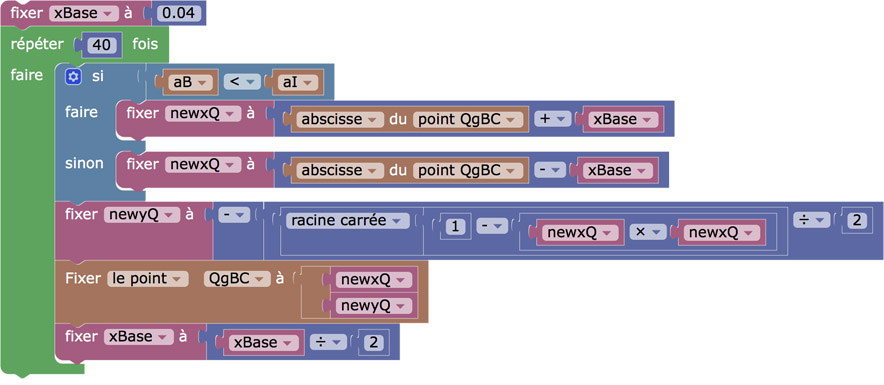
Agissant sur un point de l’ellipse, le code est encore plus compact que le précédent. On a choisi 40 répétitions, cela permet d’aller jusqu’à la précision du logiciel et ainsi obtenir la marque de l’angle droit (comme illustré ci-dessus) produite par le logiciel pour confirmer l’orthogonalité entre le segment \([PgAB \; QgAB]\)et le rayon du cercle passant par \(B\), et donc le parallélisme de \((PgAB \; QgAB)\) avec la tangente. On voit dans le code que l’ordonnée de \(QgBC\) est négative. On s’en souviendra dans la manipulation directe de la prochaine figure : \(QgBC\) doit toujours être, à l’écran, en dessous de \(F\).
Bien entendu, comme dans la figure précédente pour le point \(B\), dès que l’on a lancé le programme une fois, \(QgBC\) devient un point libre quand on déactive le programme. Mais on peut reprendre la figure initiale dans l’iframe. Voici deux illustrations de manipulation :
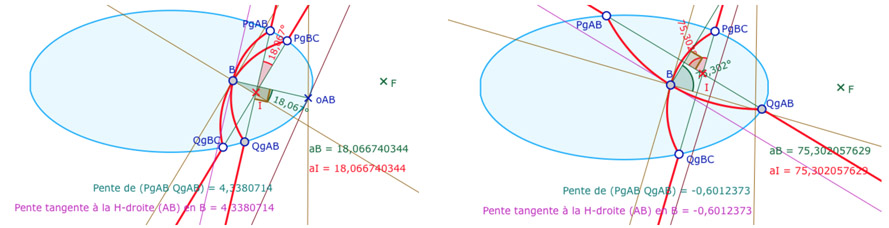
La figure est robuste, on peut s’amuser à faire passer \(PgAB\) «par dessus» \(PgBC\) (ci-dessous à gauche). Si on pousse trop loin \(PgAB\), comme sur l’illustration de droite, les angles affichés, et mesurés ne sont plus les bons, car l’arc \((Pg_{AB} Qg_{AB})\) est concave, mais leurs supplémentaires. La figure construit néanmoins toujours des triangles de Hilbert à somme 180° avec un sommet à l’intérieur de l’ellipse.
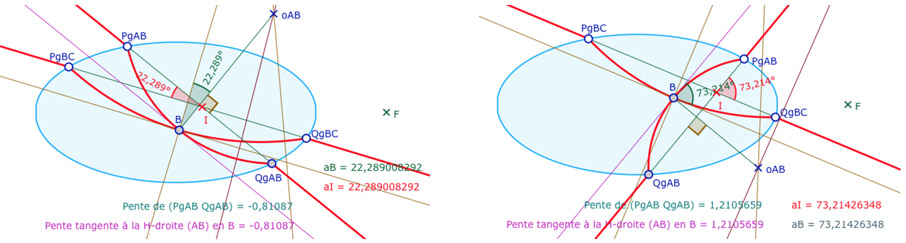
On peut par contre avoir les deux arcs concaves (en conservant \(QgBC\) en dessous de \(F\)) comme ci-dessous à gauche, et, en ajoutant une adaptation sur l’affichage des angles, on peut avoir l’arc \((Pg_{BC} Qg_{BC})\) concave avec l’autre convexe, comme illustré ci-dessous à droite. Cette situation correspond à la première abordée de cette page, avec \(aU+aV=0\) car les deux angles \(aU\) et \(aV\) sont nuls.
Manipulation de la figure associée
On n’a pas placé les points \(A\) et \(C\) pour disposer d’une plus grande ellipse à l’écran.
Rappel du mode d’emploi
• Dans cette figure on peut agir largement sur les deux points \(PgAB\) et \(PgBC\).
• On agira sur \(QgBC\) seulement avant de lancer le programme. On a vu dans la figure précédente qu’il suffit de relancer la figure dans l’iframe pour retrouver son statut initial comme «point sur objet de l’ellipse».
• Ne pas oublier que \(QgBC\) doit rester à ordonnée négative.
• Explorer toutes les variantes mentionnées dans les illustrations précédentes.
La même figure, sans environnement « responsive », dans un nouvel onglet