On a déjà signalé que \(ch_{48} = 1+\sqrt{2} \). C’est donc une valeur bien plus importante que les \(ch(r_{np})\) déjà rencontrés. Il en résulte que, contrairement aux pages précédentes, on ne pourra pas finaliser ces deux pavages pour qu’ils puissent être entièrement dans la surface, mais on peut réaliser quelques figures partielles autour de ce thème au moins pour illustrer où sont les difficultés.
Cette page va, en définitive, être un peu l’antithèse de ce site, qui prône la réalisation de figures en manipulation directe. En effet, on va utiliser ces figures – dynamiques bien entendu – plus pour préparer des illustrations qui rentrent dans les contraintes voulues. Les figures sont disponibles à la manipulation pour le lecteur de cette page, mais elles sont tellement, dans certaines situations, à la limite des contraintes de la surface pseudosphérique, qu’elles ne sont que des figures pour explorer des micro-variantes des situations proposées. On détaillera cela dans le déroulé de la page
Deux carrés de P(4,8)
Commençons par quelque chose de simple. On place tout de suite le centre du cercle sur la feuille précédente à la feuille principale, soit dans un intervalle d’amplitude \([-3\pi,-\pi[\), sinon on n’ira pas au delà de la construction de deux carrés. Et commençons par cela, simplement deux carrés, car dans ce cas on peut agir sur tous les paramètres de la figure. Voici quelques premières illustrations.
On voit que l’on peut placer deux carrés avec ce cercle de pavage pour des valeurs élevées du paramètre \(p\)
Manipulation de la figure
Dans cette figure on peut agir sur tous les paramètres. Comme dans les figures précédentes, les carrés sont tracés
même s’ils sortent de la PSH. On cherche donc des réglages qui maintiennent la figure sur la PSH.
C’est aussi une des raisons que l’on présente régulièrement des vues de dessus, car elles permettent de vérifier que tous les points sont sur la surface pseudosphérique.
Préférer ouvrir cette figure dans un nouvel onglet.
Un demi pavage de P(4,8)
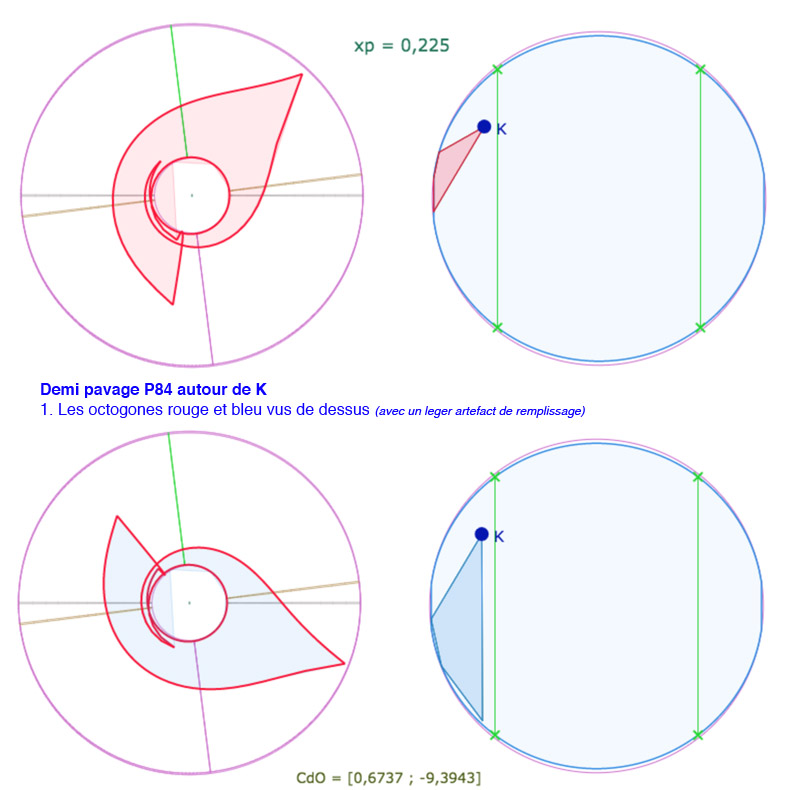
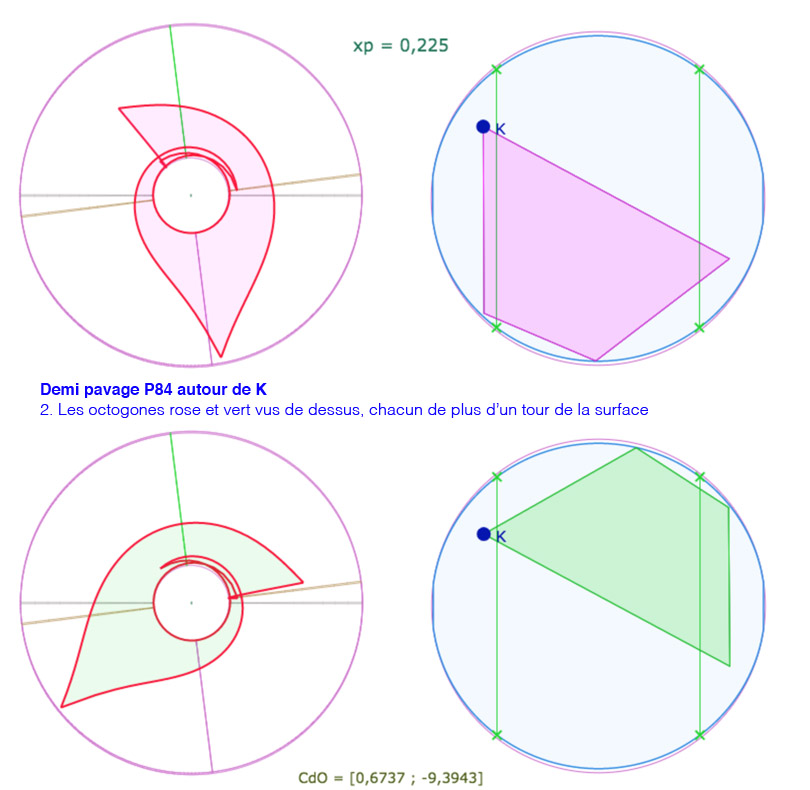
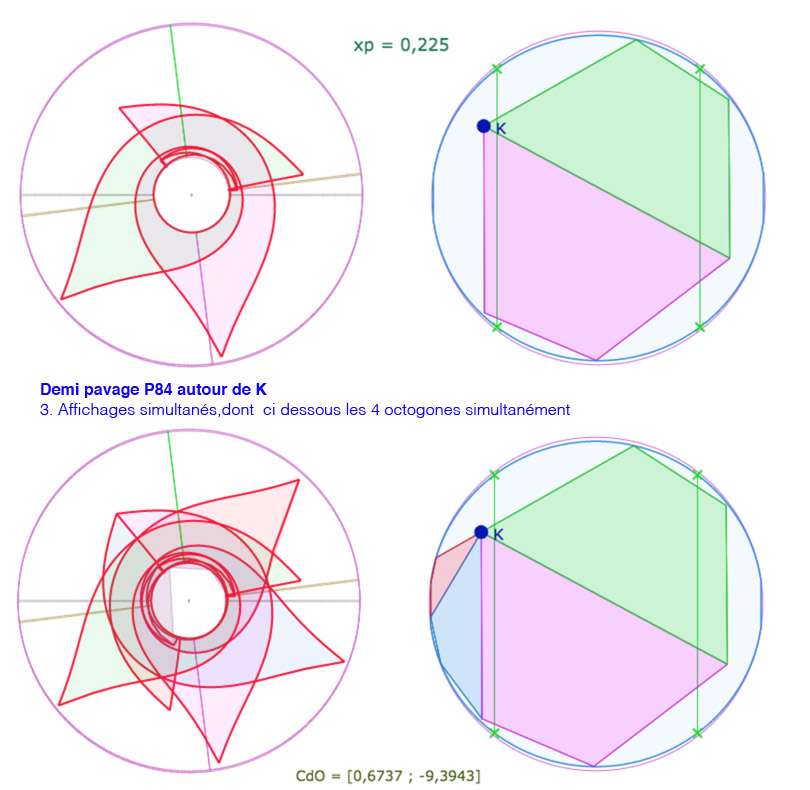
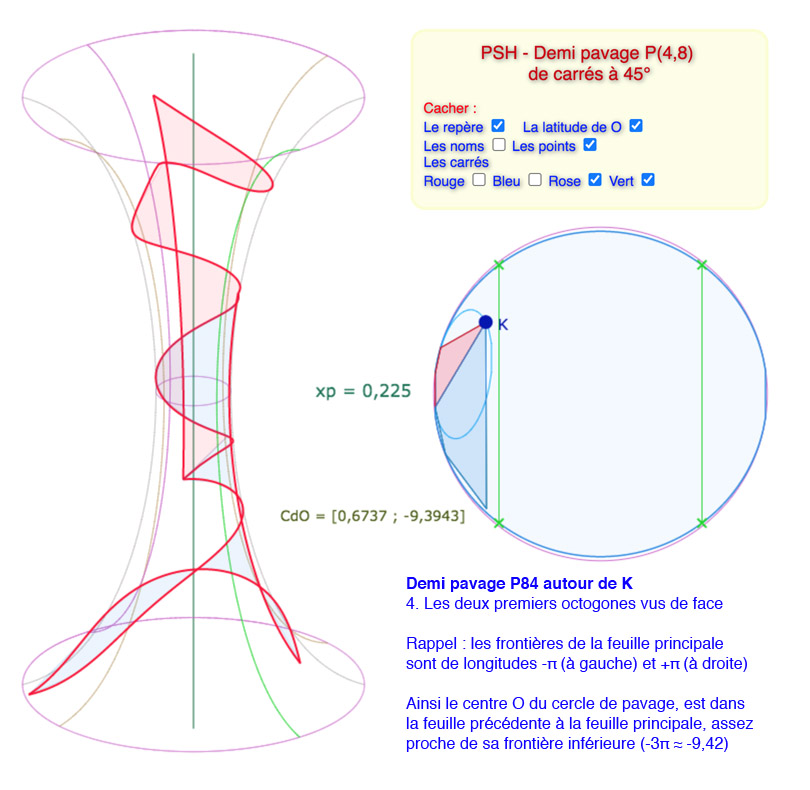
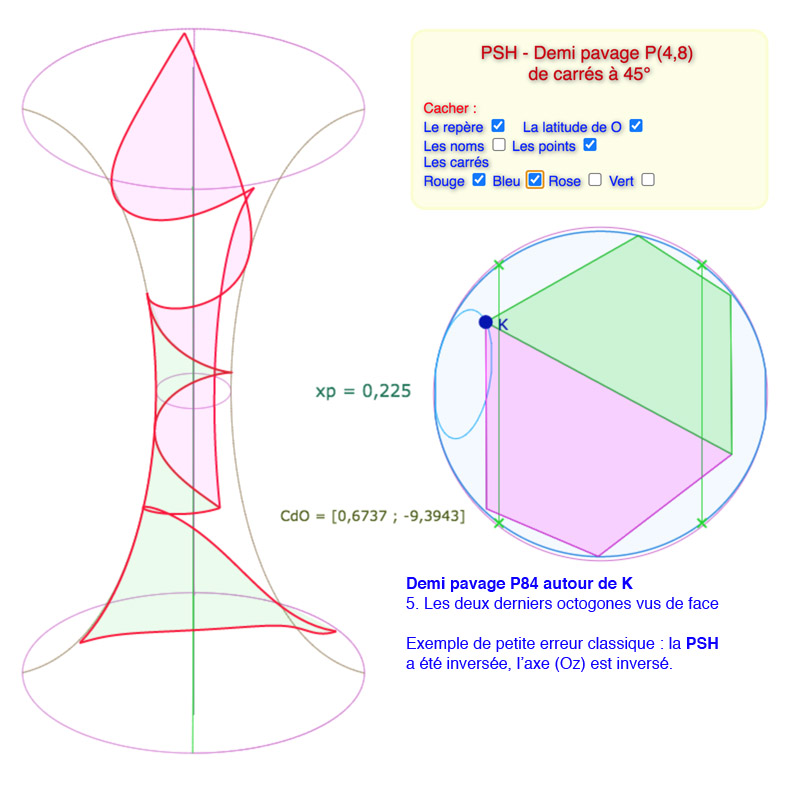
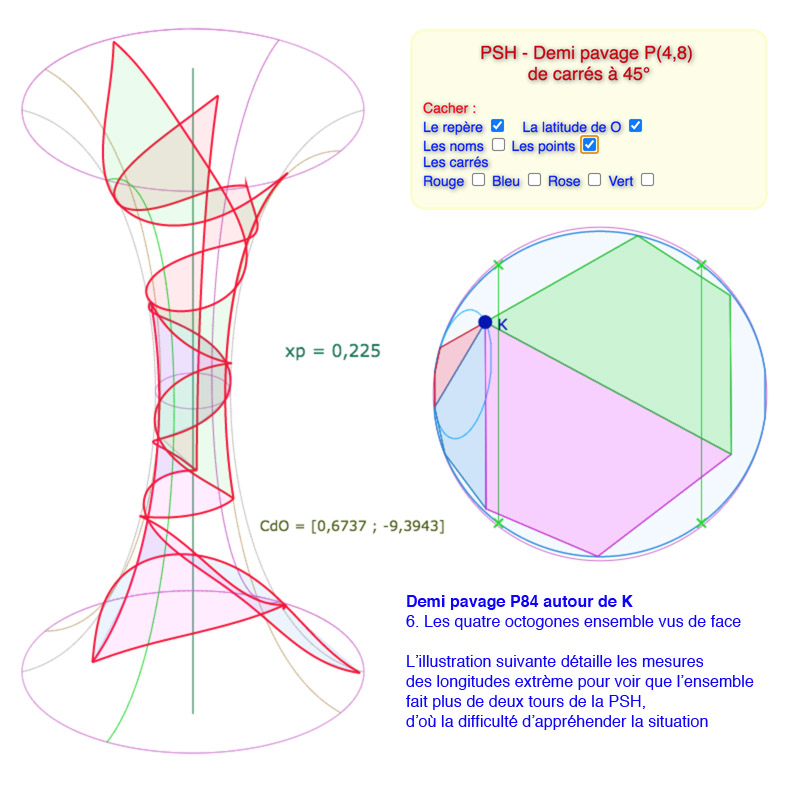
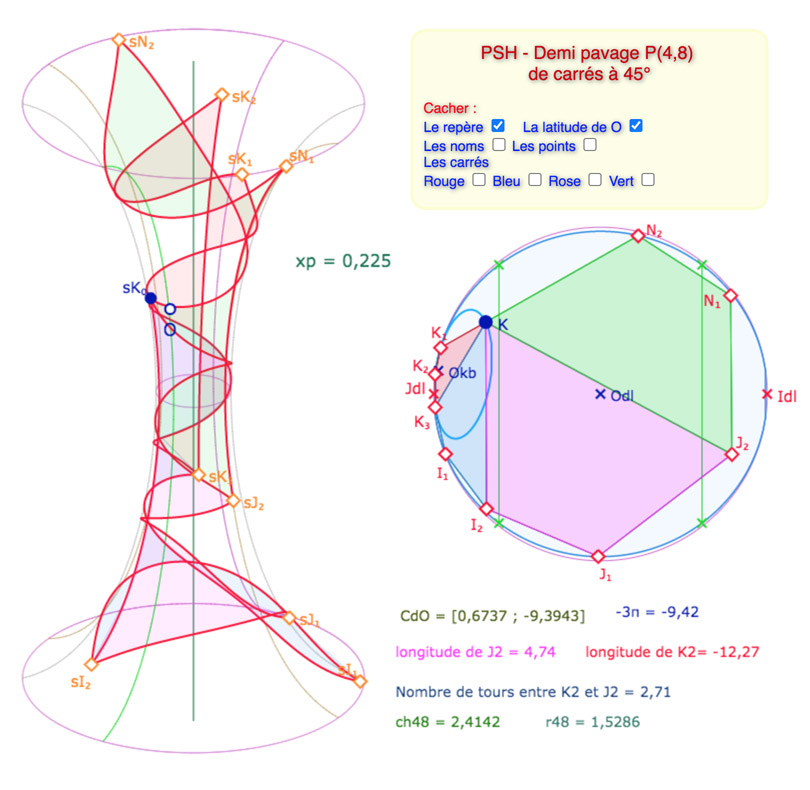
L’objectif est de faire entrer 4 carrés consécutifs de P(4,8) autour d’un point entièrement sur la pseudosphère hyperbolique avec une valeur de \(p\) la plus élevée possible. Cela dit il faut descendre en dessous des valeurs manipulables au « curseur p », et donc, on agit directement, et numériquement, sur la variable \(xp\). Voici une galerie de 7 illustrations autour d’un réglage pour \(p=0,225\), valeur de \(p\) quasi maximale (on peut tester néanmoins 0,226 et 0,227)
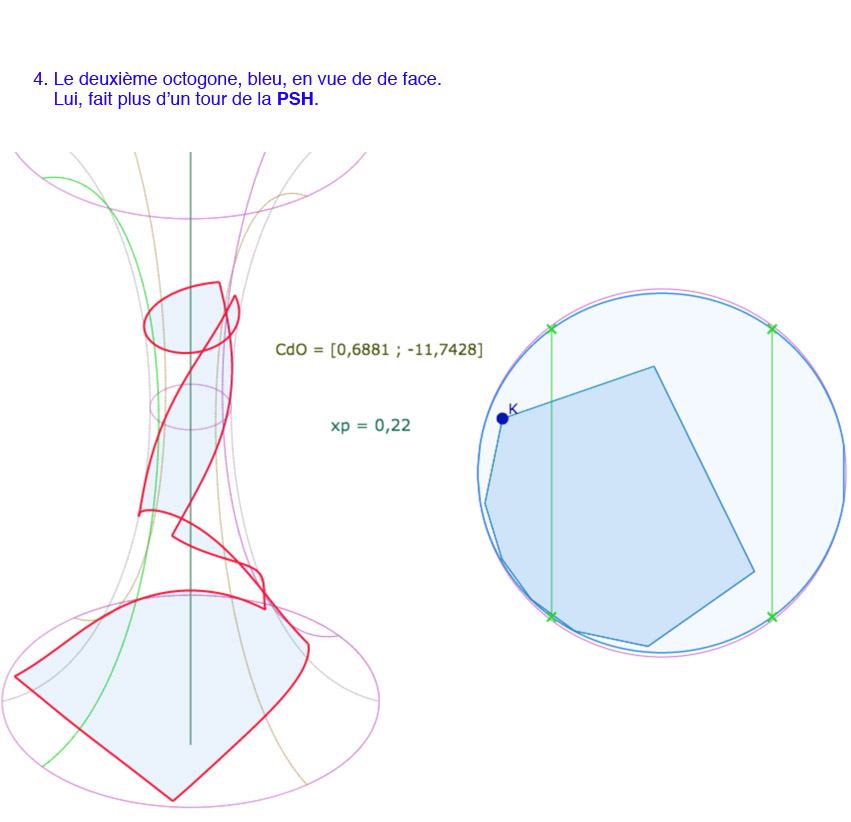
Sur la dernière illustration, on détaille l’amplitude des longitudes : ce demi pavage s’étend sur plus de deux tours.
La figure est trop haute pour être ouverte dans une iframe, on l’ouvrira dans un nouvel onglet. Penser à être en mode consultation (désactiver la flèche gauche), sans outil du tableau de bord sélectionné, pour agir sur l’orientation de la pseudosphère hyperbolique simplement d’un doigt ou au clic.
Modifier la densité des lieux
La figure est configurée avec une densité de 200 pour tous les segments sur la PSH, au lieu de 20 ou 50 dans les pages précédentes. Si vous trouvez trop lents vos modifications de la figure , vous pouvez diminuer cette densité. Pour cela, avec le mode inspecteur d’objets actif (sélectionner la roue), il faut provoquer une ambiguïté en sélectionnant un endroit où il y a plusieurs segments , en pratique autour d’une « intersection-écran »(sinon on on sélectionne que les carrés) en en choisir un.
Ensuite sélectionner « appliquer à tous » avant de modifier la densité (mettre 100 ou 50)

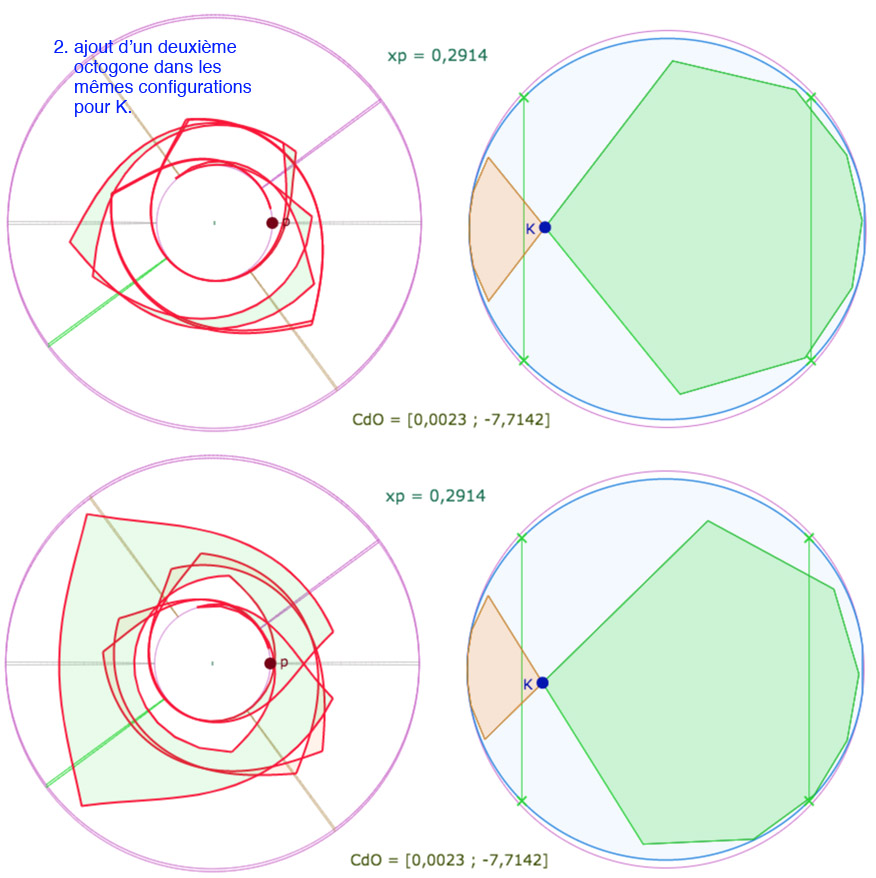
Deux octogones de P(8,4)
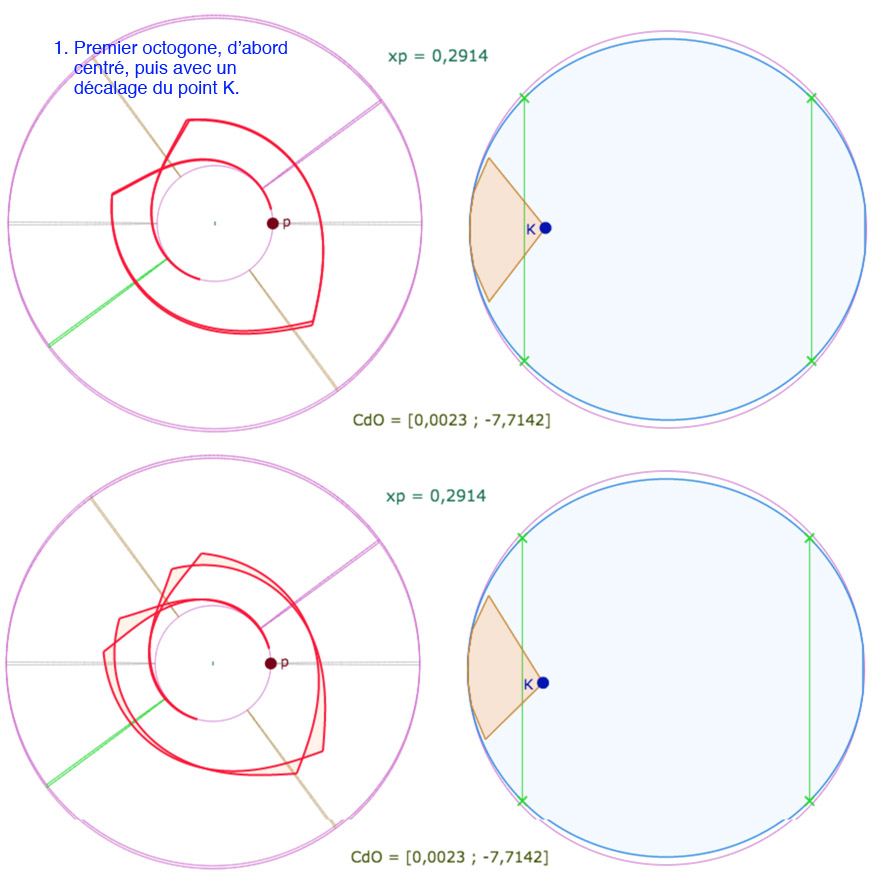
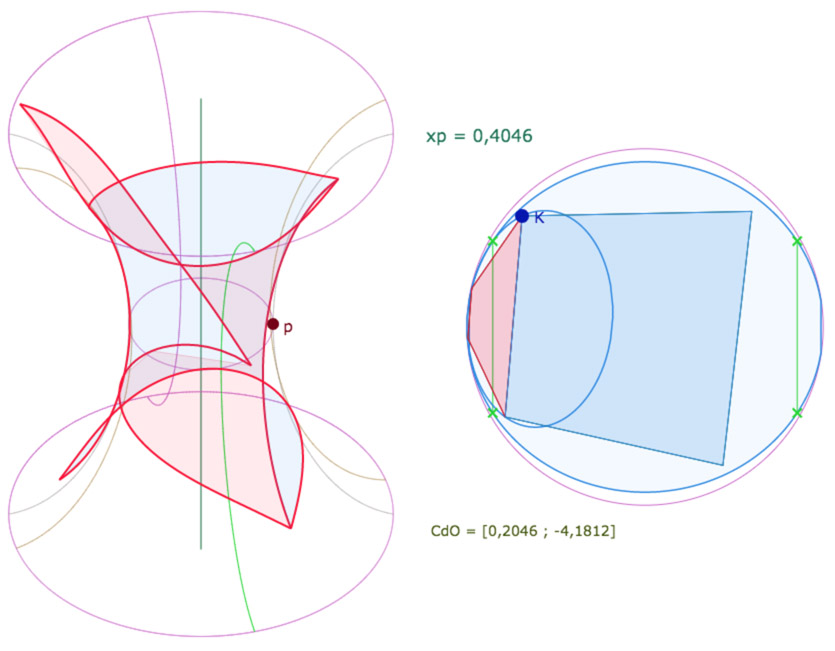
Là encore, le centre du cercle est sur la feuille avant la feuille principale. Voici directement une première figure sur laquelle on peut agir sur de nombreux paramètres, y compris le paramètre \(p\). Attention toutefois à éviter que le point \(K\) ne soit pas un sommet de l’ellipse (le KB-cercle de pavage, presque à axe vertical) car alors K disparaît … et toute la figure avec. Si cela arrive, il suffit simplement de relancer la figure depuis l’icone de recharge de l’iframe.
En affichant les points, on peut déplacer \(O\), ou à modifier sa latitude \(u_O\), ainsi que \(K\) ou \(p\) .
Préférer ouvrir la figure dans un nouvel onglet
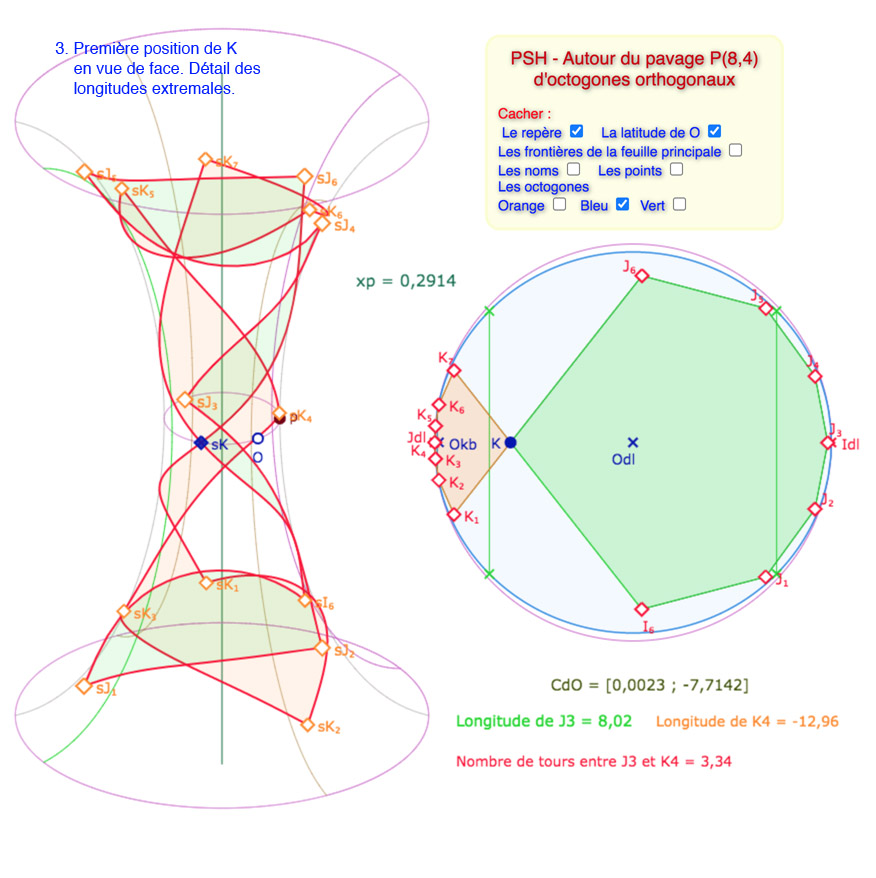
Illustration d’une configuration pour p=0,47 (centre du cercle avant la feuille principale)

Lancer la figure règlée sur cette configuration dans un nouvel onglet

Le centre placé sur la feuille précédente (deux feuilles avant la feuille principale)
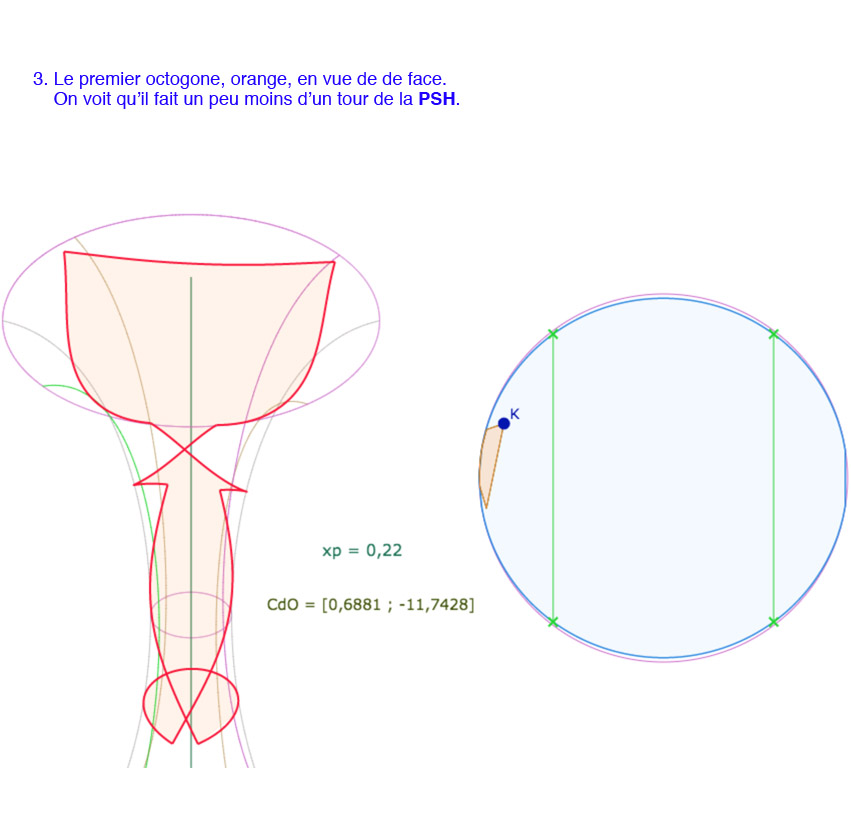
Dans ce cas, il convient de vérifier que l’octogone orange est bien entièrement sur la surface, ce n’est pas une évidence (pour certaines valeurs de \(p\)). La vue de dessus est un moyen facile, et souvent esthétique.

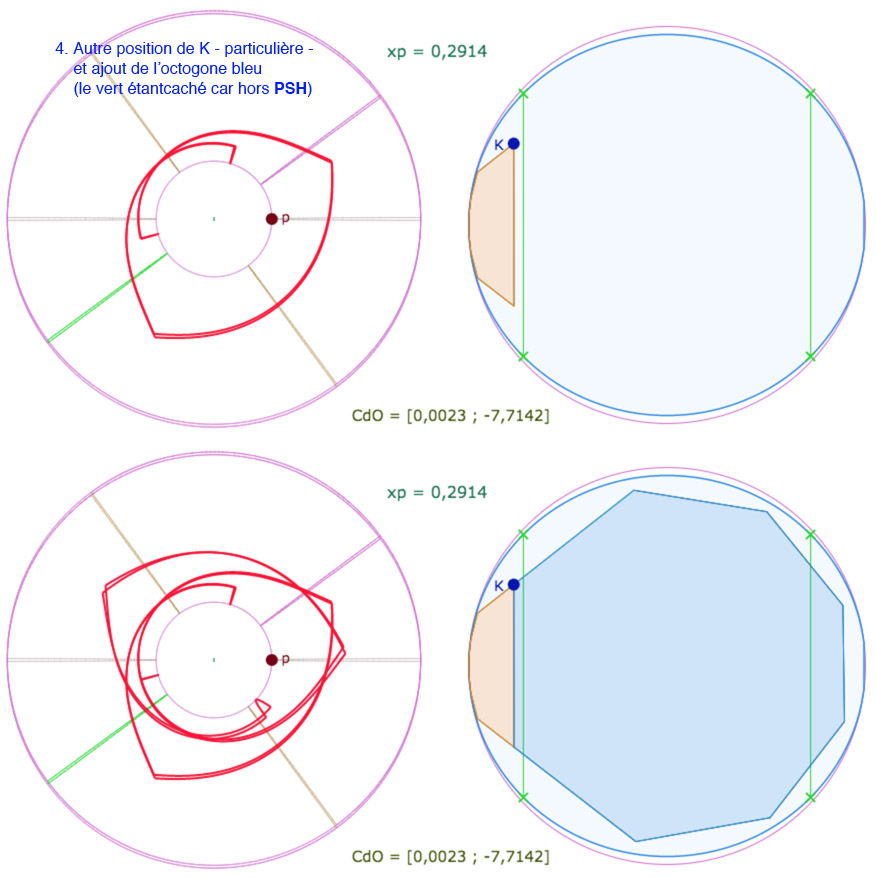
Ouvrir la figure correspondante dans un nouvel onglet. Cette figure permet aussi, pour des valeurs numériques de \(p\) inférieures à 0,25 d’explorer ce qui est présenté dans la prochaine section : on peut ainsi faire apparaître l’octogone vert. En pratique on affiche l’octogone orange et, selon la configuration le bleu ou le vert.
Une tentative de trois octogones de P(8,3) autour d’un point
On n’arrive pas à placer trois octogones autour d’un point, si on se limite à des surfaces d’un paramètre \(p >0,2\) pour être réaliste en terme de simulation. Mais on peut construire les trois octogones et choisir de n’en faire apparaitre que deux des trois. Dans ce cas on peut avoir \(p\) supérieur à la valeur minimale, et donc jouer sur \(p\) en manipulation directe. On peut ainsi obtenir tout simplement des configurations comme dans les illustrations suivantes où l’on ne fait que modifier l’orientation de la PSH et le point \(K\).
En particulier dans les 5 illustrations de cette galerie, le centre du cercle de pavage ne change pas.
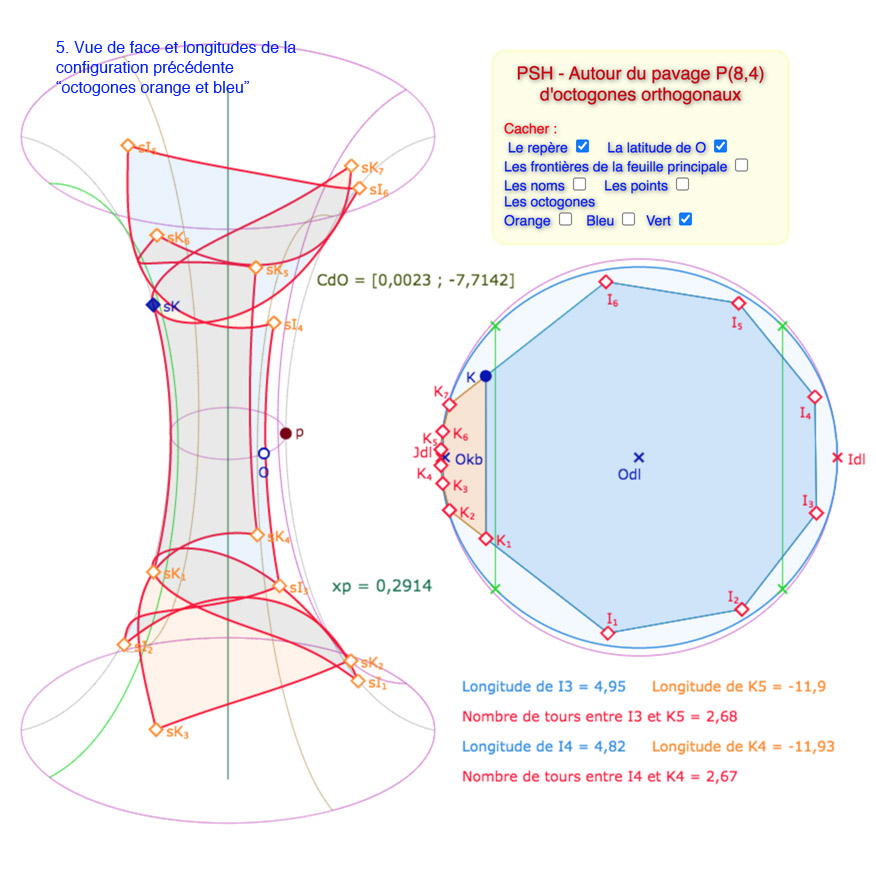
Bien entendu, l’octogone caché n’est que … caché. Dans la figure suivante, on peut s’amuser à regarder à quoi il ressemble,
mais ce n’est pas non plus signficatif car il est « hors PSH« .
Manipulation de la figure générale
La figure est trop grande pour une ouverture dans une iframe. Ouvrir cette figure dans un nouvel onglet. Le principe d’utilisation est de déplacer les points \(O, u_O, K\) et \(p\) pour que deux des trois octogones, celui orange, et l’un des deux bleu ou vert soient entièrement dans la pseudosphère hyperbolique. Ne pas oublier à être en mode consultation (la flèche à gauche désactivée).
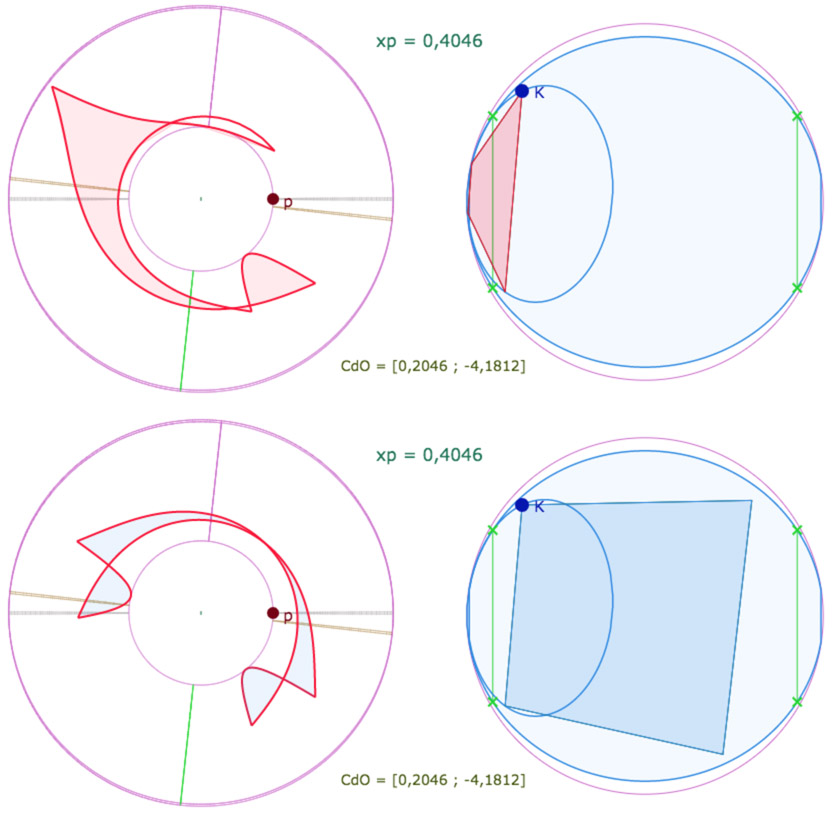
Autres illustrations pour de grandes valeurs de \(p\)
On peut arriver à trouver des situations surprenantes comme celle-ci, pour \(p=0,41\). Cette valeur de \(p\) rend le cercle de pavage minuscule, la manipulation de \(K\) devenant impossible : il faut alors anticiper, placer \(K\) à une position adéquat pour des valeurs de \(p\) plus petites (et le cercle plus grand) puis augmenter \(p\). Si \(K\) disparaît – et la figure avec – il peut réapparaître en déplaçant légèrement la latitude \(u_O\). On comprend bien qu’on est là aux limites des possibilités du logiciel (ou de la simulation).


Rappel : la figure de la section précédente – celle réglée sur \(p=0,21\), de manière manuelle (avec l’expression \(xp\)) permet les mêmes manipulations que la figure de cette section : on peut afficher les trois octogones orange, bleu et vert.
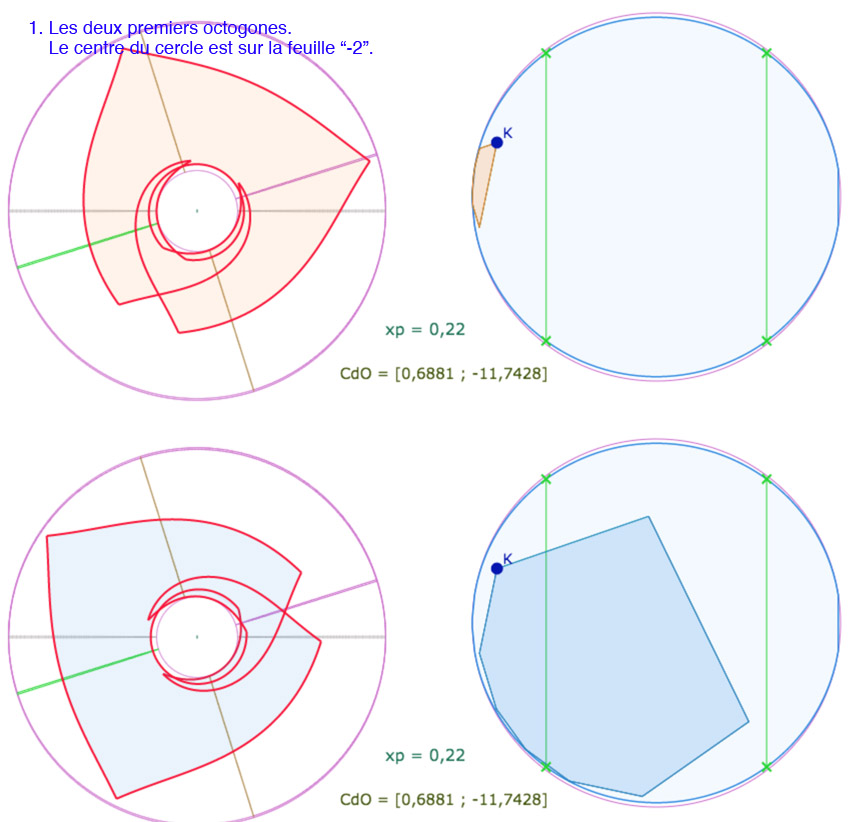
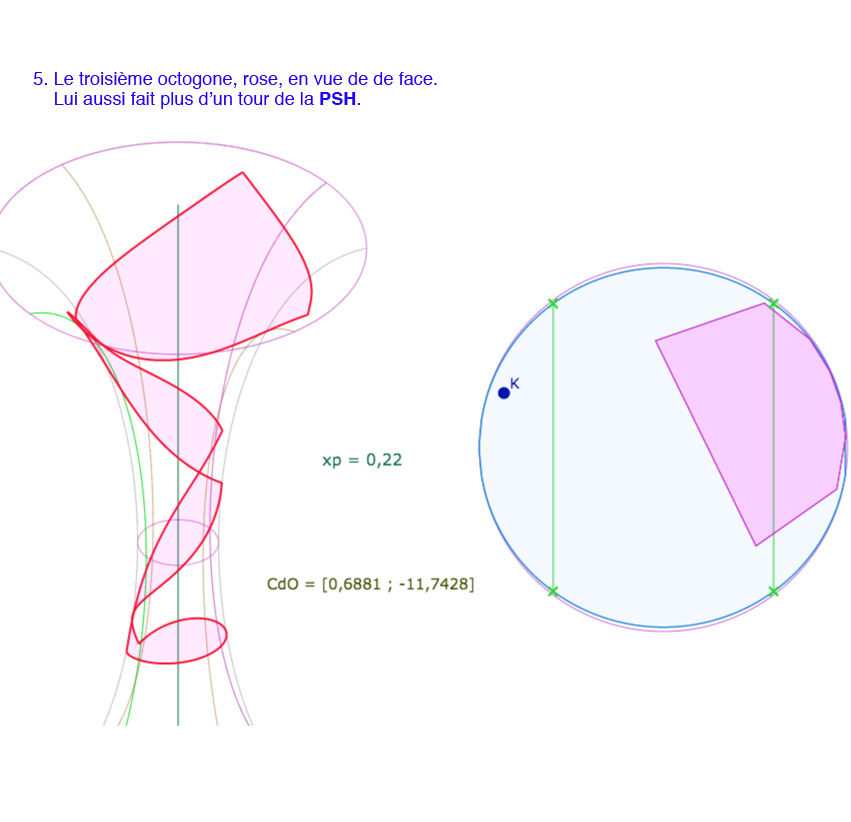
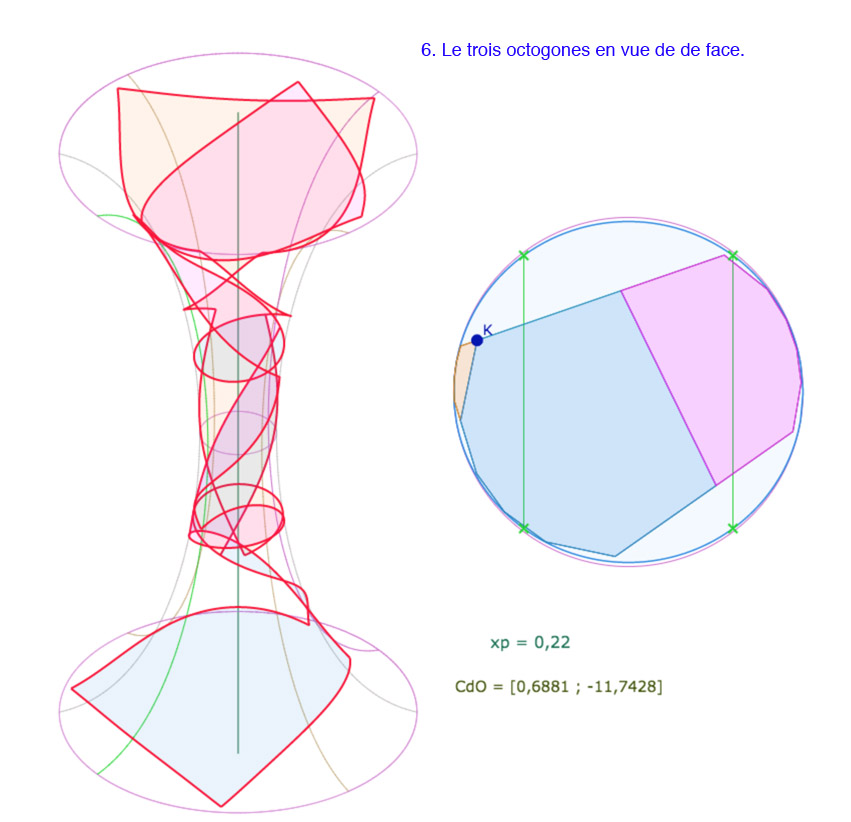
Trois octogones « alignés » de P(8,4)
S’il semble bien difficile – dans la manipulation des figures précédentes – de placer un troisième octogone autour de \(K\), qui s’insèrent tous les trois sur la pseudosphère hyperbolique, on peut plus facilement ajouter un troisième octogone, mais « à côté » du bleu, au sens de « dans l’alignement » des deux premiers.
Par contre, il faut placer le centre du cercle sur la feuille avant la feuille précédente de la feuille principale, on dira la feuille « -2 » (la feuille « 0 » étant la feuille principale). Dans les illustrations suivantes, on a enlevé le cercle de pavage. Par ailleurs, il faut une valeur de \(p\) petite, en dessous des valeurs manipulables à la souris. On présente ici une réalisation pour \(p=0,22\).
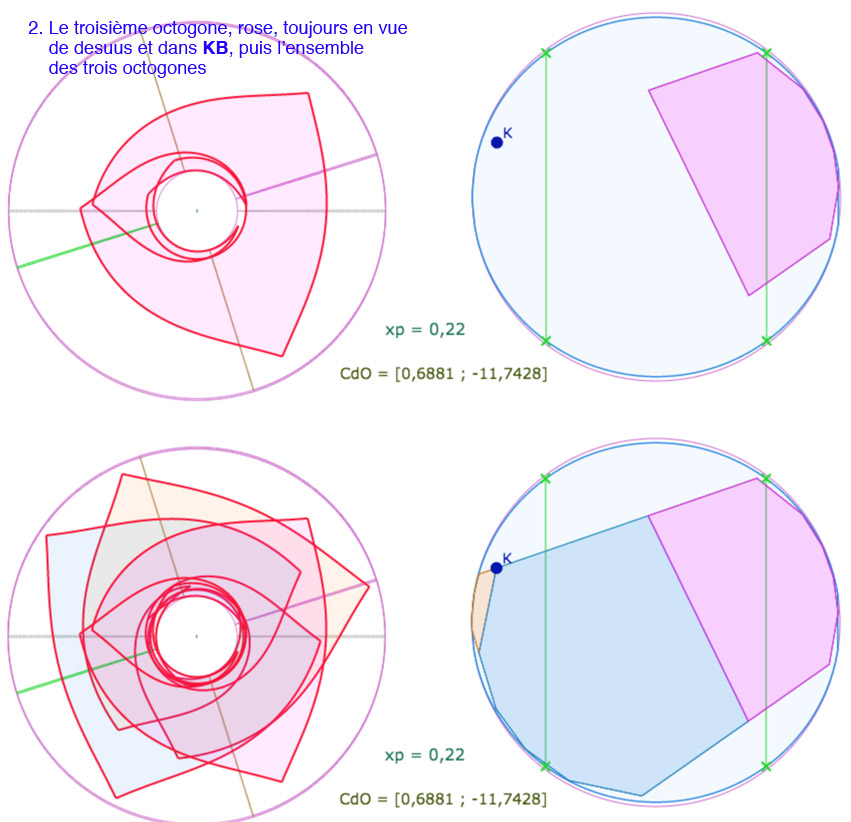
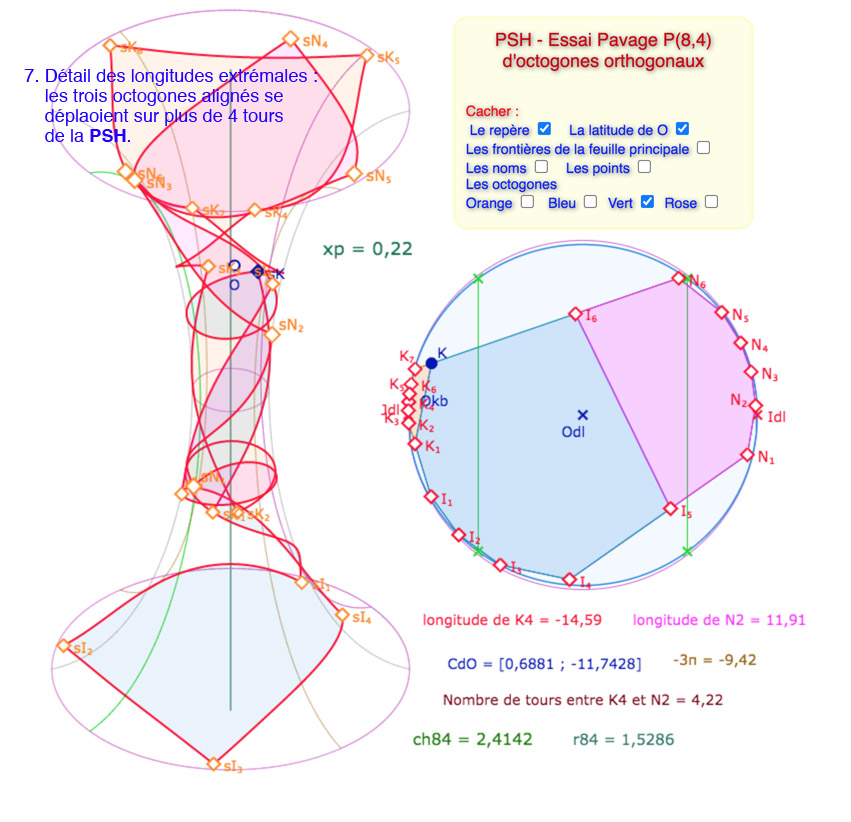
Voici une galerie de 7 illustrations, la dernière montrant deux choses :
• Que l’ensemble construit s’étend sur plus de 4 tours de la surface.
• Ce troisième octogone rose, est en fait un quatrième, l’octogone précédent, le vert de la section précédente, est toujours présent, mais caché.
Illustration de ce que l’on peut explorer avec la figure suivante
Comme pour d’autres configurations où \(p\) est petit, la surface est assez grande (haute). La figure manipulable est proposée à ouvrir dans un nouvel onglet. Désactiver la flèche du curseur standard avant de manipuler la figure.
On peut tenter, avec des valeurs de \(p\) plus petites, d’essayer de placer les 4 octogones entièrement dans la surface, en affichant l’octogone vert. Même avec \(p=0,21\) je n’y suis pas arrivé, mais c’est encore à explorer. Ce serait très intéressant à obtenir.
Densité des lieux
Comme une figure précédente sur P(4,8), on a choisi de densifier les lieux, à 200 (au lieu de 50 au maximum dans les autres pages) car les segments tournent beaucoup autour de la surface. Si la figure est trop lourde, selon le matériel utilisé, utiliser le même procédé déjà détaillé plus haut pour réduire à 100 ou 50.