Distance et équation de cercle
En géométrie hyperbolique, il y a trois types de cycles, correspondant à l’image d’un point par l’un des trois types de pinceaux de droite : les cercles, pour les pinceaux à centre, les équidistantes pour les pinceaux à axe, et les horicycles pour les pinceaux dits « sans support », c’est-à-dire les pinceaux de droites parallèles. Cette page est consacré aux cercles, la suivante aux deux autres types.
La distance sur la pseudosphère
Elle est donnée par une formule analogue aux birapports rencontrés dans le modèle projectif de Klein ou les modèles conformes de Poincaré :
\(AB = \displaystyle \left\vert th^{-1}\left( \frac{\theta_A + c_{AB}}{k_{AB}}\right)-th^{-1}\left( \frac{\theta_B + c_{AB}}{k_{AB}}\right) \right\vert = \displaystyle \frac{1}{2} \left\vert ln \left( \displaystyle \frac{1+\displaystyle\frac{\theta_A + c_{AB}}{k_{AB}}}{1-\displaystyle\frac{\theta_A + c_{AB}}{k_{AB}}}:\frac{1+\displaystyle\frac{\theta_B + c_{AB}}{k_{AB}}}{1-\displaystyle\frac{\theta_B + c_{AB}}{k_{AB}}}\right) \right\vert\)Le cercle de centre A de rayon R
Après calculs, c’est le lieu des points \(M(u,\theta)\) tels que : \(\left( ch(u) – ch(R) ch(u_A)\right)^2+(\theta-\theta_A)^2=sh^2(R)ch^2(u_A)\)
ce que l’on paramètre, comme dans le cas euclidien, avec un angle \(\varphi\) sur un intervalle d’amplitude \(2\pi\) par :
\(\left\lbrace \begin{array}{1} ch(u) &=& ch(R)ch(u_A)+sh(R)ch(u_A)cos \varphi \\ \theta &=& \theta_A +sh(R)ch(u_A)sin \varphi \end{array} \right.\)
Le cercle circonscrit à un triangle pseudosphérique
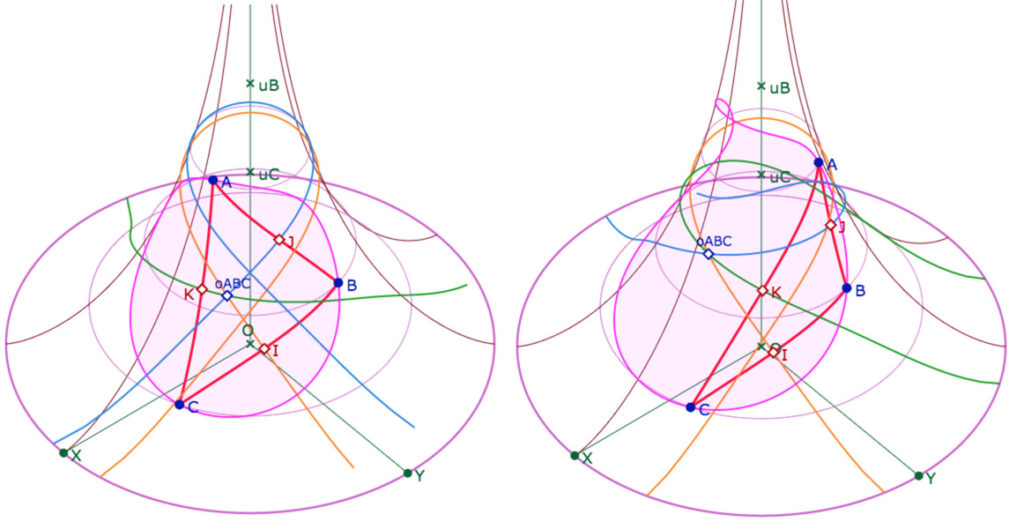
à gauche le centre du cercle circonscrit est à l’intérieur du triangle, à droite, à l’extérieur …
mais il peut être aussi sur la feuille précédente comme ci-dessous
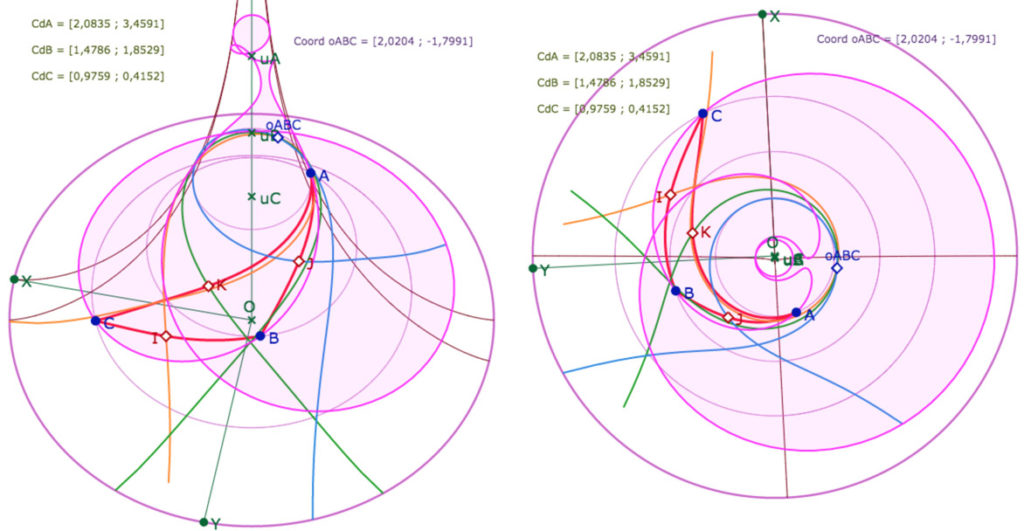
Rappel : la longitude est la seconde coordonnée. Ici, \(A, B\) et \(C\) sont sur la première feuille (par construction)
et on lit que \(o_{ABC}\) est sur la feuille précédente avec une longitude autour de \(\displaystyle -\frac{\pi}{2}\) comme on le voit bien à droite.
Manipulation de la figure
Manipulations usuelles – Tourner la pseudosphère pour accéder à la laltitude de \(A\) .
Préférer ouvrir la figure dans un nouvel onglet
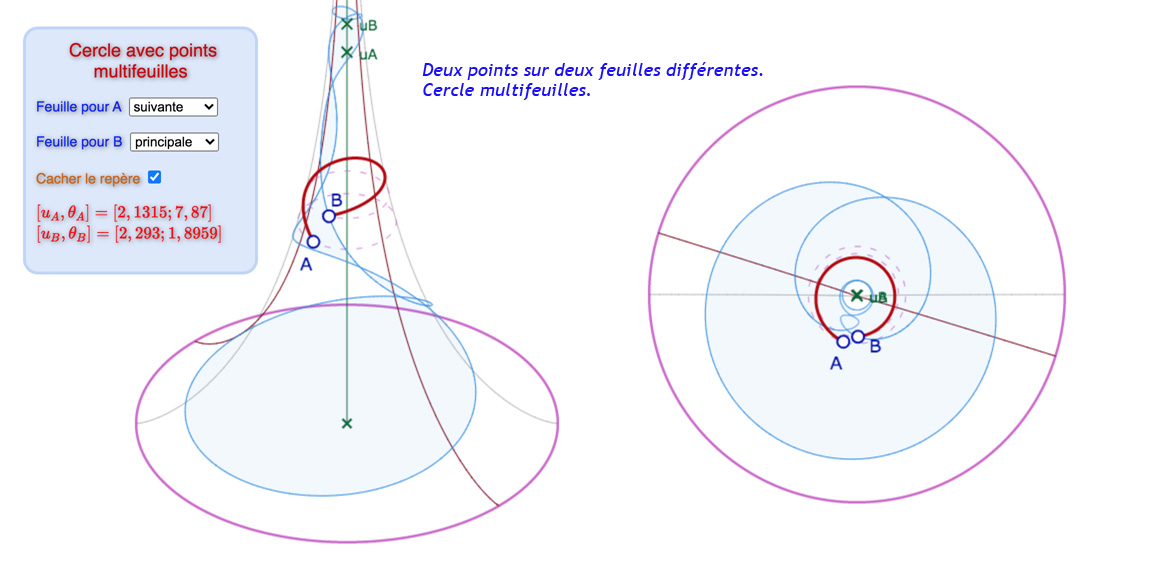
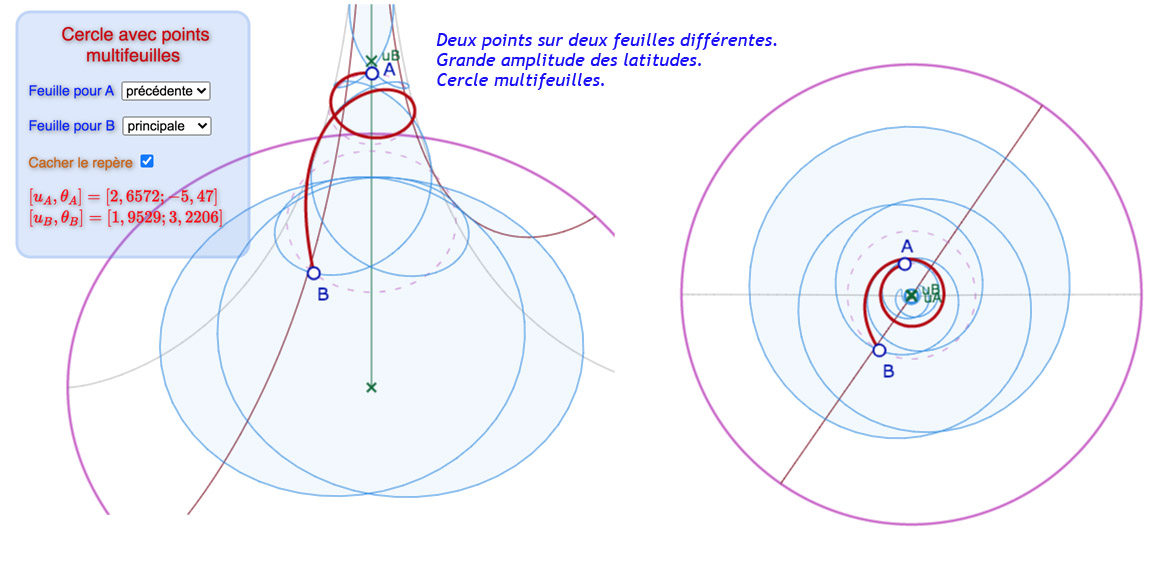
Configurations autour des cercles multifeuilles
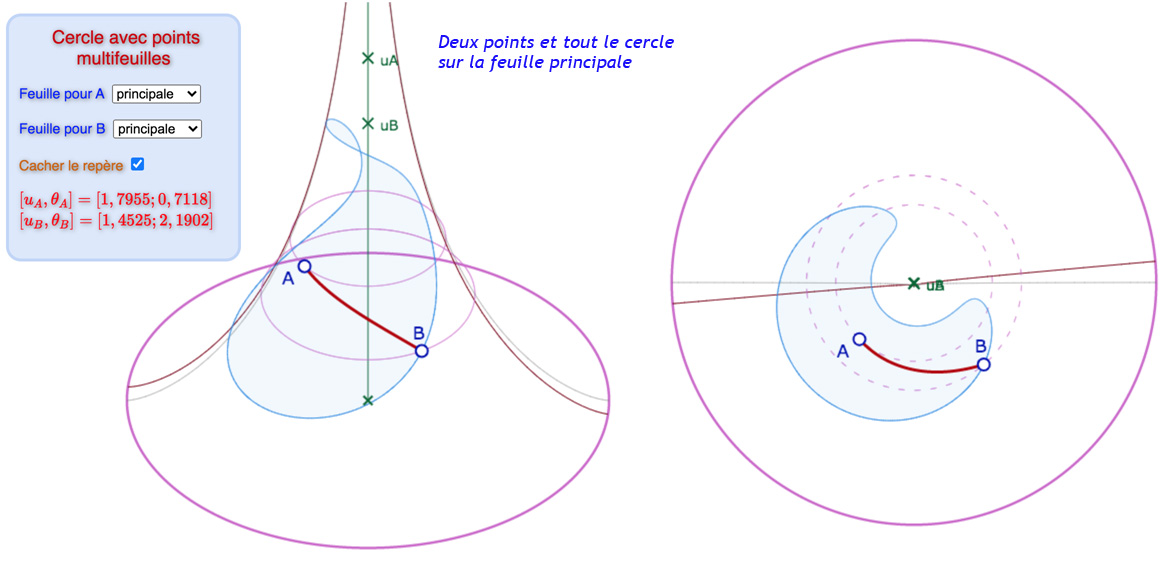
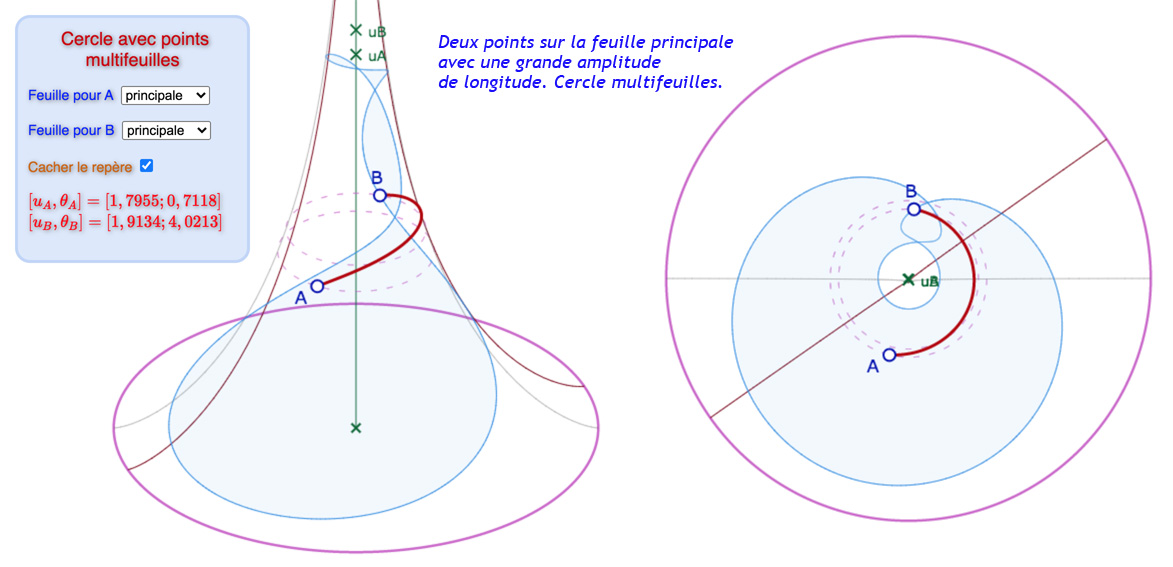
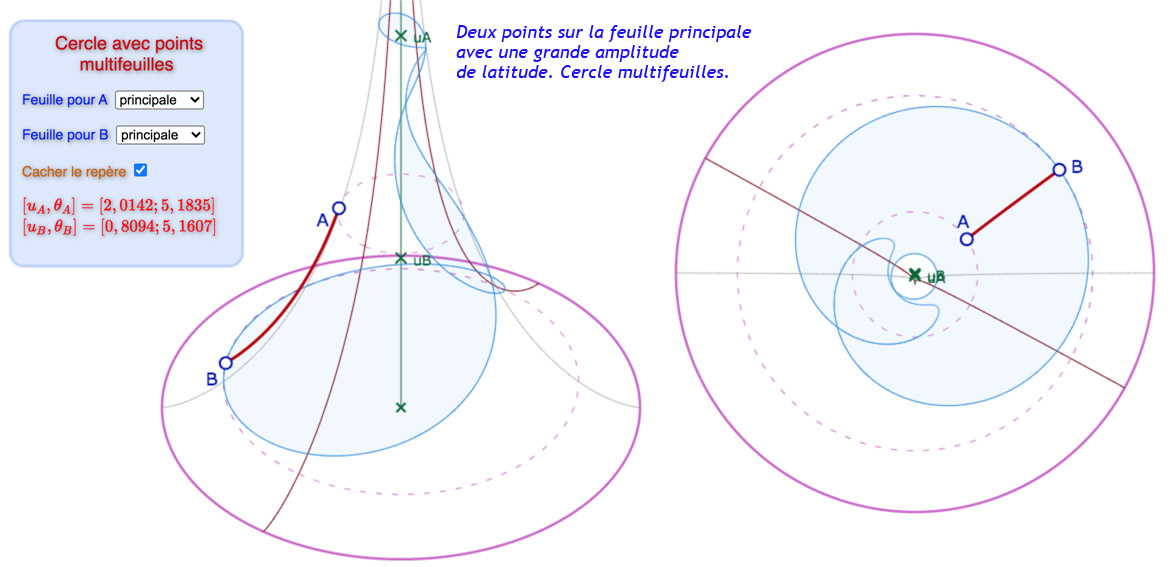
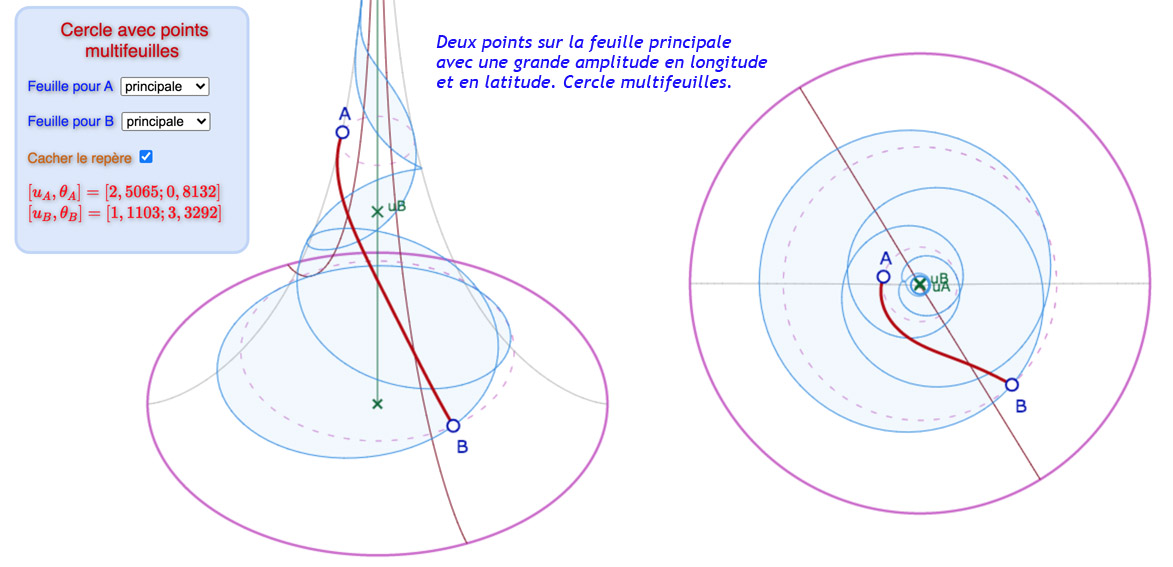
Dans la figure suivante, on peut jouer à placer les points les deux feuilles autour de la feuille principale. On évitera les cas où le cercle sort de la pseudosphère (non traité dans la macro du cercle), il y a de nombreuses possibilités d’exploration en restant entièrement sur la surface. Les illustrations ci-dessous donnent un aperçu de ce que l’on peut rencontrer. Mais en pratique c’est surtout intéressant de déplacer les points pour voir comment le cercle s’enroule sur plusieurs feuilles quand les amplitudes (de longitude ou de latitude) augmentent.
Galerie de 6 illustrations de cercles dont les constituants peuvent ne pas être sur la même feuille
La figure de manipulation
On peut s’entrainer à reproduire les illustrations précédentes
Préférer ouvrir la figure dans un nouvel onglet