L’activité sur le site en 2024-2025
(la présentation du site est après cette MAJ)
Premier semestre 2025 – Fin 2024
Le début 2025 a été concentré à la finalisation du projet commencé en septembre 2024 : traitement dynamique du régionnement du plan selon l’orthogonalité dans le modèle de Hilbert de géométrie non arguésienne. L’objectif est de réaliser une figure qui renvoie – dynamiquement – les 6 régions possibles du plan selon les perpendiculaires possibles.
On a commencé par la mise en place des trois premières régions (second semestre 2024)
Introduction au régionnement et cas 2H et 2H1E
Le cas 1H1E
Et cette page de blog qui détaille la démarche pour le cas 1H1E
Puis, à partir de mai 2025, les trois autres parties ont été mis en ligne peu à peu – d’abord sur instagram, puis avec beaucoup d’illustrations, dans cette page
Les régions 1E 1H et 0P avec mise à disposition de la figure dynamique associée … dont voici une illustration
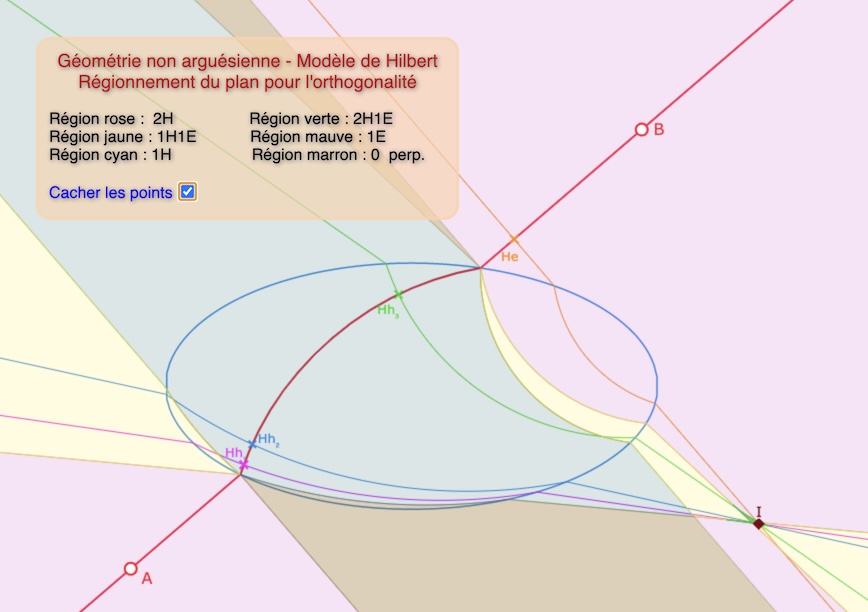
Configuration avec 4 des 6 régions : il n’y a pas les deux premières traitées 2H et 2H1E.
Plusieurs vidéos sont aussi disponibles sur le compte Instagram dédié.
On notera que quand, en 2019, nous avons commencer à explorer ce modèle non arguésien avec DGPad, cette étude sur l’orthogonalité paraissait alors techniquement juste hors de portée. Aussi, même si tout ceci n’est clairement qu’une première approche qui demande à être améliorée, c’est déjà un résultat intéressant pour au moins se représenter clairement la situation.
Premier semestre 2024
En février 2024, une collaboration avec Dominique Tournès a permis de reconsidérer le modèle de Hilbert de géométrie non arguésienne d’une manière entièrement algébrique, en réalisant une construction algébrique des droites et de leurs perpendiculaires.
Le début d’année a été consacré à réaliser les outils nécessaire à explorer plus avant cette géométrie, exploration qui a donné lieu à des découvertes passionnantes, sur lesquelles finalement a été consacrée toute l’année, d’autant que des approches dynamiques impossibles à envisager avant l’approche algébriques sont désormais explorables. Cinq pages ont d’abord été réécrites au premier semestre 2024 :
Droites de Hilbert et applications
Orthogonalité
Triangles orthocentriques
Triangles bi-orthocentriques et orthocentriques ayant deux hauteurs parallèles
Ces pages, pas ou peu techniques sont accompagnées d’articles de blog, nettement plus techniques qui détaillent les démarches utilisées :
• Construction algébrique de la droite du modèle non arguésien de Hilbert (mars 2024)
• Réalisation de diverses macros du modèle non arguésien de Hilbert (mars 2024)
• Construction de triangles bi-orthocentriques de Hilbert ayant deux hauteurs parallèles (mai 2024)
Autres productions début 2024 … avant le modèle de Hilbert
Le corps des extrémités de Hilbert des plans hyperboliques (janvier 2024)
Utilisation des macros du disque de Poincaré (dont le pavage P73 ou encore P237 – janvier 2024)
Optimisation et utilisation des macros de géométrie elliptique (janvier 2024)
Présentation express des GNE
sur Instagram
sous forme de carrousels (galeries de 10 images) sur ce compte Instagram (février 2024) et vidéos.

Et bien entendu , après mai 2024, l’essentiel des publications est consacré à la géométrie non arguésienne de Hilbert comme on le voit dans les 5 dernières productions, dont 4 vidéos, les deux dernières étant sur le régionnement. Avant il y a eu 6 vidéos sur la construction de Malfatti.
Introduction au site
Ce site est consacré aux Géométries Non Euclidiennes (GNE dans la suite), et plus précisément à la manipulation de figures dynamiques. C’est essentiellement un site consacré aux configurations, non technique (avec très peu de mathématiques en fait, sauf dans le dernier menu Bachmann) construit autour de figures « à manipuler ». Il est d’abord organisé de pages fixes, de présentation de ces géométries – l’essentiel de la première livraison de mars 2022 – et est ensuite complété par des articles, eux, généralement plus techniques.
Même si on peut picorer un peu partout dans les menus, le site est quand même construit pour être parcouru – même partiellement – plus ou moins dans l’ordre des menus dont on présente ci-dessous les orientations générales.
Il peut être intéressant aussi de consulter un article de présentation dans MathemaTICE illustré de copies d’écran de ce site, qui propose une visite structurée en 7 parcours différents, du plus généraliste au plus spécifique.
Les menus de « GNE avec DGPad »
Précisons, tout d’abord, que les titres des menus sont eux-même des pages de présentation de ces menus, souvent de construction du modèle utilisé. Il convient de les lire en premier, ceci pour tous les menus.
DGPad : menu de présentation rapide du logiciel utilisé. Pour manipuler les figures du site, il suffit de consulter les deux premiers items Utilisation des figures et Utilisation des macros. Les items suivants sont plus techniques. Ils abordent de vraies problématiques de la géométrie dynamique qui pourront être rencontrés ici ou là et présentent les solutions retenues.
Modèles : ce menu propose tout d’abord deux modèle bornés de la géométrie euclidienne, un plan et un de l’espace. C’est l’occasion de se familiariser à la fois avec le logiciel et avec cette notion de modèle tout en restant dans un environnement connu. Ces deux modèles, le disque euclidien borné et la sphère épointée, sont proposés car le premier sera comparé au modèle elliptique et le second servira pour illustrer le passage par l’horisphère dans le mémoire de Bolyaï. Ce menu se poursuit par des considérations plus conceptuelles, avec des modèles finis, d’abord affines et euclidiens avant d’aborder, dans le dernier item, un modèle hyperbolique fini intéressant à illustrer dynamiquement.
DP : ce menu est consacré à la géométrie hyperbolique dans le modèle du Disque de Poincaré. Il est conseillé de commencer l’exploration des GNE par ce menu, car c’est ici que sont présentés les concepts qui seront systématiquement utilisés dans les autres menus (droites en faisceau, faisceau de droites, cycles divers et trilatères). L’intérêt de la géométrie dynamique est dans l’exploration individuelle des concepts présentés. Ce menu est partiellement organisé sur cette exploration par l’utilisateur, parfois même en proposant que le lecteur ait la possibilités de finaliser lui-même certaines figures … même si elles sont aussi proposées finalisées.
PS (PseudoSphère) : ce menu illustre l’apport de Beltrami aux GNE avec le mémoire dans lequel il montre que la géométrie intrinsèque des surfaces à courbure constante négative est naturellement « la géométrie de Lobatchevsky », c’est-à-dire la géométrie hyperbolique. Beltrami le fait, en particulier, sur la surface de révolution la plus simple à étudier, la pseudosphère. Ce menu est construit en deux parties. Tout d’abord une approche de « géométrie intrinsèque des surfaces » où l’on calcule tous les éléments sur la surface. Puis une seconde partie aborde la conjugaison avec le modèle de Klein-Beltrami (KB présenté dans un item « interlude ») qui correspond à ce que Beltrami appelait le Disque Limite (DL dans les figures). La conjugaison est l’occasion de réaliser quelques belles figures qu’on ne pourrait pas construire directement sur la pseudosphère.
PSH (PseudoSphère Hyperbolique) : On aborde ici un autre modèle hyperbolique, avec une autre surface de révolution. Son intérêt est que cette surface couvre une partie beaucoup plus grande du plan hyperbolique que la pseudosphère ordinaire, qui plus est avec une seule feuille. Cette particularité permet d’aborder d’autres questions que dans le menu précédent et donc de réaliser des figures assez originales. Comme pour les autres menus, le titre est une page à consulter en premier – ici de présentation de la construction de la surface.
Ce menu se termine par deux pages sur la PSE (PseudoSphère Elliptique) qui a cette particularité – comme son nom l’indique – de ne recouvrir qu’une partie bornée du plan hyperbolique sans aucun contact avec l’infini.
Ell : le menu de la géométrie Elliptique, une géométrie bornée, non orientée, bien plus éloignée de nos représentations géométriques que le cas hyperbolique. Tout comme DP, ce menu est partiellement construit autour de l’exploration par l’utilisateur de ce que deviennent les concepts présentés dans DP avec cette géométrie. De belles choses sont à découvrir ici, faciles d’accès et si loin de ce que l’on peut imaginer en géométrie.
Non Arg : On doit à David Hilbert d’avoir introduit plusieurs géométries particulières dans son ouvrage « Les fondements de la géométrie ». Ce menu aborde deux modèles de la géométrie Non Arguésienne, le modèle proposé par Hilbert lui-même (MaJ avril 2024), et le modèle de Moulton, plus simple à étudier. On verra qu’ils ne sont pas équivalents.
Comme ces géométries sont assez peu étudiées, et probablement pas en géométrie dynamique, tous les résultats développés pour les constructions de Moulton sont précisés pour d’autres utilisations éventuelles ou pour aller plus loin.
Bachmann : Ce menu a été ajouté de mars à juin 2023. On distinguera deux parties :
• la première partie de ce menu présente quelques aspects simples de l’axiomatique de Bachmann, avec des illustrations hyperboliques et elliptiques . Ce menu est « plus mathématique » que tous les précédents, au sens où l’on reprend en détail le cheminement de Bachmann avec les démonstrations effectives de ses premiers théorèmes. On y présente aussi sa façon originale de séparer les géométries.
• la seconde partie, centrée sur le plongement projectif de la géométrie absolue de Bachmann – est, comme le reste du site, rédigée d’un point de vue uniquement culturel, avec beaucoup d’illustrations et de figures à manipuler, sans reprendre les démonstrations de Bachmann.
Ce menu sur l’axiomatique de Bachmann terminé, on a ensuite prolongé ce thème – et on le poursuivra – dans des articles de blog, sur quelques détails techniques ou autres résultats plus théoriques.
Les articles du site – Perspectives
Dans la première publication de mars 2022, l’essentiel a été concentré sur le contenu des menus du site. Ils sont plus ou moins « définitifs », sauf améliorations partielles s’entend (par exemple de nombreuses figures sur la PSH ont été refaites en juillet 22, suite à une nouvelle technique développée pour l’enroulement d’un cercle sur plus de 200 tours autour de pseudosphère) .
Depuis la mise en ligne initiale, plus de 30 articles ont été réalisés. Ils sont souvent plus techniques que le contenu des menus. Parfois il s’agit d’articles sur des points précis non traités avant pour éviter d’alourdir les menus des géométries.
Dans un premier temps, l’accent a été mis sur la présentation de l’utilisation des macro-constructions qui ont permis la construction des figures. C’est le partage du plaisir de faire des figures dynamiques de GNE, bien entendu avec des figures préconstruites facilitatrices. Ces articles ont été rédigés pour l’ensemble des modèles présentés (Modèles DE et Horisphère, puis DP, Ell, PS, PSH, KB, Non Arg Hilbert, Non Arg Moulton).
Dans le même temps, nous avons commencé a rédiger des articles sur l’approche très originale – que l’on nomme dans ce site KEKH – proposée par Daniel Perrin d’un modèle projectif plan, d’une part du plan elliptique, modèle que l’on nomme KE (Klein elliptique) et d’autre part d’un plongement de KB dans le plan projectif (structure que l’on nomme KH pour Klein Hyperbolique). Ce thème sera régulièrement complété. Actuellement 5 articles sont disponibles. Le dernier (octobre 2022) aborde le spin d’un triangle, outil créée par Daniel Perrin pour étudier les « cas d’égalités » des triangles dans le cas non euclidien.
Ensuite, à partir de novembre 2022, on a commencé une série d’articles sur le mémoire de Bolyai dont la seconde partie – et le second article – traite de la quadrature hyperbolique du cercle. Un troisième article aborde le calcul et la construction du rayon des cercles de pavage – avec de très belles figures – souvent utilisés dans le menu PSH par exemple.
La réalisation algébriques des droites de Hilbert, et de leurs perpendiculaires, dans le modèle non arguésien de Hilbert, début 2024, va recentrer l’activité du site sur ce modèle, probablement pendant toute l’année 2024.
A propos du nom de domaine … bizarre
Le nom de domaine curvica974 a été crée en lien avec le compte Twitter du même nom @Curvica974. Les deux avaient été créés pour traiter de ce puzzle Curvica que l’on utilise à l’IREM de La Réunion, avec de superbes plateaux en bois.
Toutefois, depuis, le logiciel de géométrie dynamique DGPad a beaucoup évolué, avec l’arrivée de Blockly en 2016, et, depuis cette date, le compte Twitter de Curvica, s’était recentré vers l’utilisation de DGPad. Désormais, le compte twitter traitera plutôt de l’activité sur ce site.
Il est prévu d’ajouter les outils de bases des blogs, mais cela n’est pas encore réalisé. En attendant, on peut commenter le site sur Twitter @Curvica974 ou écrire directement par mail à l’auteur – pour proposer des améliorations/corrections/suggestions par exemple – avec l’adresse suivante soit sur gmail ou sur orange : (yves)(point)(martin)(quarante cinq en chiffres).