Cet article est le premier d’une série consacrée à une approche radicalement différente des GNE que celle développée dans les menus de ce site. Elle a l’intérêt de se centrer sur ce qui est commun à la géométrie elliptique et à la géométrie hyperbolique, alors que nous avons, au contraire, montré dans les pages des menus, à quel point elles sont différentes. Clairement, pour voir des points communs il faut changer de point de vue, et même de lunette. C’est ce que nous propose de faire Daniel Perrin avec le point de vue projectif et ses lunettes préférées, les formes quadratiques. Que l’utilisation de la géométrie projective ne rebute pas les plus jeunes lecteurs qui ne l’ont probablement jamais rencontrée dans leur formation initiale. Le point de vue est si riche qu’il mérite vraiment qu’on s’y attarde.
Daniel Perrin, regardant le plongement projectif du disque de Klein-Beltrami dans le plan entier, s’est intéressé à faire la même chose pour la géométrie elliptique (d’où le KE pour Klein-Elliptique) et il y a aussi intégré le plongement de la géométrie hyperbolique (d’où le KH). Il en avait fait un petit fascicule à l’époque, d’une quinzaine de pages. Puis il a approfondi … pour en faire un livre – une somme – en 6 parties et plus de 1300 pages !
Argumentaires autour de ce choix
Commençons par quelques extraits généraux de ses diverses introductions, à différents chapitres.
Mon opinion, en effet, est que cette notion de parallèle, contrairement à ce que semblerait indiquer l’histoire, n’est pas fondamentale en géométrie non euclidienne. Pour une fois, l’histoire, à mon avis, ne fait que masquer la véritable nature des choses. Nous verrons en revanche dans la Partie V, que même avec l’entrée par la géométrie projective et les formes quadratiques que j’ai choisie, la notion de parallélisme est absolument fondamentale en géométrie euclidienne. C’est sans doute cette importance des parallèles dans le cadre euclidien et la prégnance de ce cadre sur nos habitudes de pensée qui expliquent qu’aujourd’hui encore, on mette en avant le problème des parallèles dans toute présentation des géométries non euclidiennes. J’annonce tout de suite que cela ne sera pas ma position, préférant une entrée par la géométrie projective et les formes quadratiques dont j’espère que le lecteur pourra apprécier la pertinence.
Daniel Perrin – Partie 4 – page 3 – « La géométrie d’une forme quadratique . Deuxième épisode : les GNE. »
Dans la section suivante nous présentons, de manière un peu minimale, l’argumentaire de Daniel Perrin tel qu’il est décrit et étudié en profondeur (comme d’habitude chez lui) dans la partie 4 consacrée aux GNE (PDF de 370 pages) de ce livre de 1395 pages, a priori non encore édité, mais déjà disponible en PDF, en six parties, dont le titre provisoire est « Géométrie projective plane et applications aux géométries euclidienne et non euclidiennes ». Pour Daniel Perrin, les géométries elliptique et hyperbolique ont finalement plus de points communs que l’on imagine. Voici une autre citation de la présentation de cette partie 4 :
Dans cette partie, notre point de vue consiste à traiter ensemble les géométries elliptique et hyperbolique, sur un corps quelconque. En effet, nous pensons que leurs points communs sont beaucoup plus nombreux que leurs différences et qu’en revanche elles sont radicalement différentes de la géométrie euclidienne. Dans notre approche, la raison qui motive cette opinion est que la forme quadratique qui définit la géométrie est non dégénérée dans les deux cas hyperbolique et elliptique, alors qu’elle est dégénérée dans le cas euclidien. En particulier, dans les cas non euclidiens on bénéficie d’une polarité (du moins si l’on consent à ne pas oublier les points extérieurs !) et l’on verra qu’on tient là un outil extraordinaire.
Daniel Perrin – Partie 4 p.13
On comprendra que cette série d’articles sur KE et KH qui commence ici, est aussi un – bien modeste – éloge à celui qui a si merveilleusement accompagné plusieurs générations d’étudiants soit de visu, soit à travers ses différents ouvrages.
Le point de vue de Klein
Pour Klein (1871), les géométries usuelles – celles que nous étudions ici – sont plongées dans une « géométrie mère », le plan projectif \(P^2(\mathbb{R})\). Elles se construisent – et sont différentiées entre elles – par une structure supplémentaire, à savoir par l’orthogonalité définie par une forme quadratique.
Dans ce contexte, on sait que les géométries elliptique et hyperbolique correspondent respectivement (en tout cas sur \(\mathbb{R}\)) aux formes quadratiques \(q(X,Y,T) = X^2+Y^2+T^2\) et \(q'(X,Y,T) = X^2+Y^2-T^2\). On note \(\varphi\) et \(\varphi’\) les formes polaires associées. Dans ce contexte, on appelle encore hyperbolique la géométrie du plan idéal associée à la géométrie issue de \(q’\) dont on sait que la géométrie de l’intérieur de la conique définie par \(q’=0\) est hyperbolique, c’est le modèle KB.
Fixons alors \(T=0\), comme droite de l’infini, que l’on note \(\Delta\) dans la suite. Nous sommes alors dans un plan affine, muni d’un point \(O\), pôle de la droite \(\Delta\), de coordonnées (projectives) \(O=(0,0,1)\) qui est orthogonal à \(\Delta\), à la fois pour \(q\) et \(q’\).
Dans le cas hyperbolique, l’orthogonalité pour \(\varphi’\) est la conjugaison par rapport à la conique \(X^2+Y^2-T^2=0\), soit, d’un point de vue affine, par rapport au cercle unité de Klein-Beltrami d’équation \(x^2+y^2=1\).
Rappel : \(\varphi'(x,y) = \displaystyle \frac{1}{2} \left( q'(x+y)-q'(x)-q'(y) \right)\) et par conjugaison, on entend \(\varphi'(x,y)=0\).
Or, l’orthogonalité pour \(\varphi\) s’exprime facilement à partir de celle de \(\varphi’\). En effet, notons \(\sigma\) la symétrie centrale par rapport à \(O\) : \(\sigma(x,y) = (-x,-y)\) ou encore, d’un point de vue projectif \(\sigma(X, Y, T) = (-X, -Y, T)\). On a alors \(\varphi(u, v) = -\varphi'(u,\sigma(v))=-\varphi'(\sigma(u),v)\).
Autrement dit, deux éléments sont orthogonaux pour \(\varphi\), si le premier et le symétrique du second par rapport à \(O\) le sont pour \(\varphi’\).
On peut donc ainsi facilement construire les outils projectifs d’un plan elliptique de Klein (KE) depuis le plan idéal projectif (KH) du plan hyperbolique de Klein-Beltrami (KB). C’est ce que l’on se propose de faire dans cet article.
Pré-requis technique
Dans cet article, on suppose que le lecteur a déjà parcouru (un minimum) les menus DP et ELL qui présentent les géométries hyperbolique et elliptique dans des modèles standards. Il serait utile d’avoir vu aussi la page sur le modèle KB dans le menu PS. On ne reviendra pas sur les résultats hyperboliques ou elliptiques déjà présentés.
Par ailleurs, comme il va y avoir beaucoup de figures, elles seront surtout présentées « à ouvrir dans un nouvel onglet » , en particulier car les figures sont assez grandes si on veut voir tous les points. Si le lecteur arrive sur cette page par un lien, sans jamais avoir navigué sur ce site, il conviendrait de regarder comment manipuler les figures (en particulier comprendre qu’il vaut mieux être en mode consultation). Pour cela consulter le début de cette page.
Les points et les droites dans KE et KH
Les droites de KE sont les droites affines (projectives) usuelles, et les points tous les points du plan. D’une manière générale, il n’y aura aucun problème de définition dans KE. Pour KH, la situation est moins simple puisque la forme quadratique associée admet des vecteurs isotropes. En pratique les points du plan KH sont les points du plan privé de ceux du cercle unité (car ce sont les points qui annulent la forme quadratique), et les droites sont toutes les droites sauf les tangentes au cercle unité. Ce choix largement détaillé parmi d’autres possibilités, par Daniel Perrin, est principalement justifié par le fait que ces points et ces droites ne peuvent être centre ou axe de symétrie, et donc ne peuvent être milieu (a priori, on y reviendra) ou axe de symétrie. Par ailleurs la polaire d’un point de la conique est la tangente à la conique en ce point, et, à un moment donné, il sera important que le pôle d’une droite ne soit pas incident à cette droite.
Il résulte de ce choix une situation bien particulière : l’axiome de base de toute géométrie n’est pas vérifié : par deux points, il peut ne pas passer de droite. Il suffit de prendre deux points sur une tangente du cercle. Daniel Perrin commente cette situation en ces termes :
Attention, par rapport aux textes standards sur les géométries non euclidiennes, ce livre présente une singularité. En effet, les points et les droites que nous définissons ici ne vérifient pas toujours l’axiome de base de la géométrie d’Euclide : par deux points passe une droite et une seule. Il nous semble, en effet, qu’il est préférable de renoncer à cet axiome dans un premier temps, même si le poids des traditions s’y oppose. Cette généralisation ne concerne d’ailleurs que le cas hyperbolique pour lequel elle revient à ajouter aux points du disque de Klein les points extérieurs. Dans ce cas, on verra que le surcroît d’efficacité obtenu en utilisant la polarité vaut bien quelques concessions. On verra tout au long des chapitres suivants qu’on retrouve aisément les résultats usuels en spécialisant les résultats généraux aux points et droites hyperboliques.
Daniel Perrin – Partie 4 – pages 22-23 qui précise clairement les choix retenus
Dans ce contexte, même si on rappelle souvent ici que l’on est dans un contexte projectif, deux droites de KH peuvent ne pas être sécantes. Pour cela il suffit qu’elles se coupent en un point du cercle unité. Dans ce cas Daniel Perrin parle de droites parallèles (p. 25) ce qui est en phase avec propriété hyperbolique dans KB, « par un point de KB, il passe deux parallèles à une droite de KB donnée ».
Plus loin, il propose des définitions généralisées pour réintégrer ces points et ces droites dans certains cas particuliers. Pour ce qui est de la géométrie dynamique, sauf à vouloir l’illustrer spécifiquement, on ne rencontre jamais ces cas particuliers en manipulation directe. Pour ce premier article sur KEKH, on a choisi de ne pas implémenter ces cas particuliers dans les macros. Par contre, on pourra, à l’occasion illustrer quelques cas particuliers.
Orthogonalité et symétrie orthogonale
On se donne donc un cercle unité, noté \(CU\) dans les macros, de centre \(O_{cu}\). Pour rendre les figures plus facilement manipulables – pour voir plus facilement les points en jeu parfois trop éloignés, on a choisit de prendre un cercle modifiable à la souris, donc de rayon quelconque, ce qui nécessite quelques adaptations de calculs, mais élémentaires. Étant donnée une droite \((AB)\), on construit \(P_{kh}\) son pôle par rapport au cercle et \(P_{ke}\) le symétrique de \(P_{kh}\) par rapport au centre du cercle. Ce point est le « pôle elliptique » de la droite par rapport au cercle de référence. Le point \(P_{kh}\) sera alors dit « pôle hyperbolique » s’il fallait préciser. Cette composée de l’inversion et de la symétrie centrale par rapport au centre rappelle l’antipodie elliptique que nous avons déjà utilisé dans le modèle usuel de Klein : c’est la même transformation, mais elle s’applique à d’autres objets.
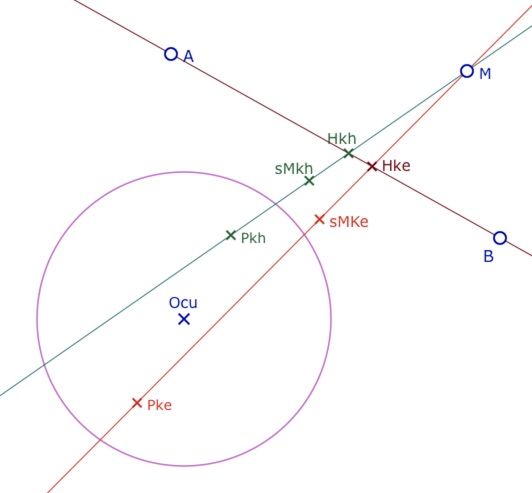
Lancer cette figure dans un nouvel onglet (penser à modifier le rayon du cercle en tirant sur le cercle)
Comme nous sommes dans une géométrie projective, toutes les perpendiculaires passent par le pôle correspondant. On construit ainsi les KH et KE perpendiculaires à \((AB)\) issues de \(M\). Les symétriques de \(M\) par rapport à \((AB)\) sont les conjugués (le 4° point de la division harmonique) de \(M\) par rapport aux pôles \(P_{kx}\) et aux pieds des perpendiculaires \(H_{kx}\). On construit ainsi les deux points \(sM_{kh}\) et \(sM_{ke}\).
Si la droite coupe le cercle unité, sa trace dans le cercle est une droite de KB, elle est alors la perpendiculaire commune à … toutes (les traces dans KB de) ces KH-perpendiculaires qui sont concourantes en le pôle de cette perpendiculaire commune.
Cas d’une droite passant par le centre du cercle
Si une droite passe par le centre du cercle, son pôle est à l’infini dans la direction orthogonale à la droite. Il en résulte que les KE et KH perpendiculaires à cette droite sont la droite euclidienne correspondante. Et donc une droite passant par le centre est « conforme pour l’orthogonalité ».
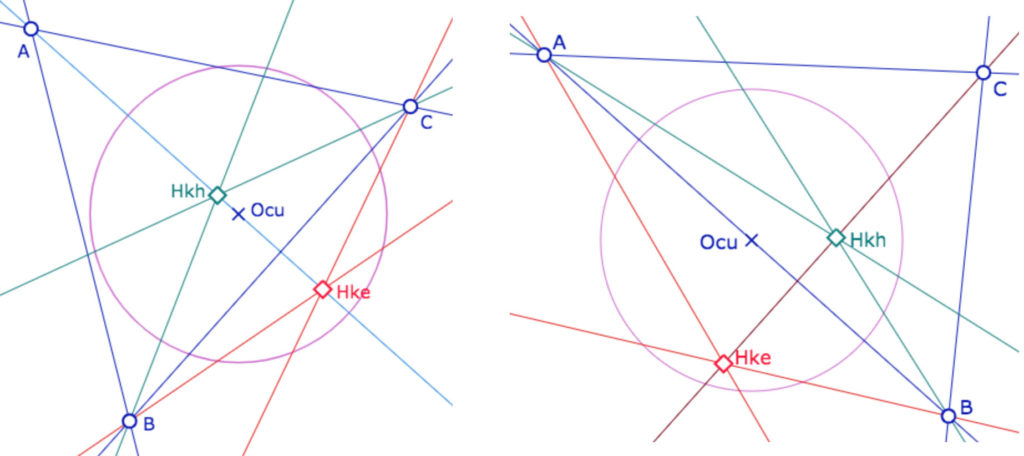
à gauche : on trace la droite \((AO_{cu})\). Par un point \(C\) on construit sa perpendiculaire euclidienne. Cette droite est aussi la KE et KH-perpendiculaires à la droite \((AO_{cu})\). Elle contient donc le point C. On poursuit la figure en traçant les autres KE et KE-hauteurs.
à droite, le triangle \(ABC\) a deux sommets sur une droite passant par le centre. Les KE et KH-hauteurs issues de \(C\) sont toutes les deux la perpendiculaire euclidienne à \((AB)\).
Application immédiate : orthocentre d’un triangle dans KE et KH
Dans cette figure, on peut déplacer les trois sommets, le centre du cercle, ou le rayon du cercle en tirant sur le cercle.
Préférer ouvrir cette figure dans un nouvel onglet

Contrairement à ce qu’on pourrait penser un peu vite, un triangle de KH n’a pas toujours un orthocentre. Cela arrive par exemple dans le cas où le point de concours des trois droites est sur le cercle unité, car ce point n’est pas un point du plan idéal KH (alors qu’il le serait pour KE). C’est très facile à réaliser : ci-contre, on se donne les deux sommets \(A\) et \(B\) et un point \(nonH_{kh}\) sur le cercle unité. La KH-perpendiculaire à \((B \, nonH_{kh})\) issue de \(A\) coupe la KH-perpendiculaire à \((A \, nonH_{kh})\) issue de \(B\) en \(C\), alors \(ABC\) n’a pas d’orthocentre car les trois hauteurs, par construction, se coupent (dans le plan projectif) en un point isotrope et donc ne se coupent pas dans KH.
Ouvrir cette figure dans un nouvel onglet.
(on peut déplacer le point sur le cercle, les deux sommets \(A\) et \(B\) et la taille du cercle)
La perpendiculaire commune à deux droites dans KE et KH
A priori, comme on est dans un modèle projectif, on doit s’attendre – y compris dans KH – à ce que deux droites aient toujours une unique perpendiculaire commune – ce qui n’est pas « standard » d’un point de vue de la géométrie hyperbolique qui, en essence, du point de vue de l’axiomatique de Bachmann, est « non connectable ». Daniel Perrin a bien précisé (après Klein) en introduction que l’on continue d’appeler hyperbolique la géométrie du plan idéal associée à la forme quadratique « hyperbolique ». Mais c’est d’abord une géométrie projective.
Dans la figure suivante \(pAB_{kx}\) est le pôle de \((AB)\) dans la géométrie KX (X=H ou K) de même pour \(pCD_{kx}\) avec la droite \((CD)\).
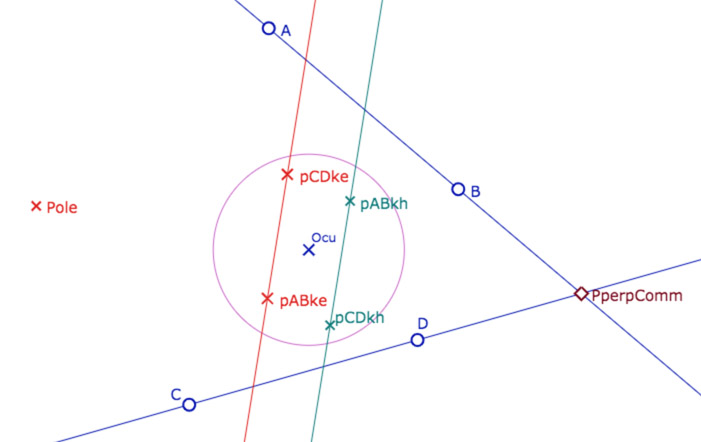
La KE et la KH perpendiculaire commune à deux droites est, chacune, la polaire de leur intersection …
… mais chacune dans le modèle concerné. En pratique l’intersection des deux droites est le pôle de la KH-perpendiculaire commune, et c’est le « pôle elliptique » de la KE-perpendiculaire commune, dont le pôle par rapport au cercle unité est le point Pôle, point dont le symétrique par rapport au centre \(O_{cu}\)du cercle est bien le point \(PperpComm\), intersection des deux droites.
Polaire et pôle elliptiques
On retiendra donc de cette figure que si la droite \((pAB_{kh}pCD_{kh})\) est bien la polaire usuelle du point \(PperpComm\) par rapport au cercle unité, la droite \((pAB_{ke}pCD_{ke})\) est alors la polaire elliptique (ou KE-polaire dans les macros) du même point, c’est-à-dire la polaire du symétrique de ce point par rapport au centre du cercle, ou encore, l’intersection de deux droites est le KE-pôle de la KE-perpendiculaire commune de ces deux droites. Ces macros de pôle et polaire elliptiques seront utilisées régulièrement dans la suite.
Ouvrir cette figure dans un nouvel onglet
En manipulant la figure, on peut visualiser que si les deux droites \((AB)\) et \((CD)\) sont parallèles (au sens euclidien usuel), alors les polaires coïncident et sont la perpendiculaire commune aux deux droites passant par le centre du cercle : c’est la polaire du point à l’infini dans la direction des droites.
Les milieux de deux points
Il n’y a pas de problème pour les points de KE : ils ont toujours deux milieux. Pour KH, il y a une condition arithmétique. En pratique \(A\) et \(B\) ne peuvent avoir un KH-milieu que si \(q'(A)\) et \(q'(B)\) ont même signe, les points étant identifiés à un vecteur. Or \(q'<0\) à l’intérieur du cercle unité et \(q’>0\) à l’extérieur. Donc deux points de KH ont un milieu si et seulement si ils sont tous les deux soit à l’intérieur du cercle unité soit à l’extérieur. Et dans ce cas, ils ont aussi un second milieu. Pour plus de précisions, on consultera le chapitre 3 de DPPartie4, à partir de la page 95.
Désormais, quand un numéro de page sera mentionné, ce sera toujours en référence à ce fichier de la Partie 4.
Si \(A(x_A,y_A)\), pour KE, on a \(q(A)=x_A^2+y_A^2+1\) et pour KH, \(q'(A)=x_A^2+y_A^2-1\).
Les calculs de Daniel Perrin (p. 91 en exercice) montrent que, du point de vue affine, le milieu (affinement) entre \(A\) et \(B\) est le barycentre de \(\left( (A, \sqrt{q(B)}), \, (B, \sqrt{q(A)}) \right)\) dans KE, de même avec \(q’\) dans KH, en ajoutant des valeurs absolues aux expressions sous les racines carrées. Le second milieu est alors le conjugué de celui-ci par rapport aux deux points \(A\) et \(B\). Pour KH, concrètement, on peut écrire la condition d’existence de manière un peu brutale (avec le sinon NaN) mais efficace, comme ceci :
(d(A,Ocu)-CU)*(d(B,Ocu)-CU)>0?(B*sqrt(abs((x(A)-x(Ocu))^2+(y(A)-y(Ocu))^2-CU^2))+A*sqrt(abs((x(B)-x(Ocu))^2+(y(B)-y(Ocu))^2-CU^2)))/(sqrt(abs((x(A)-x(Ocu))^2+(y(A)-y(Ocu))^2-CU^2))+sqrt(abs((x(B)-x(Ocu))^2+(y(B)-y(Ocu))^2-CU^2))):NaN
Dans l’illustration suivante, les points de préfixe I sont les milieux affinement intérieurs aux deux points, construit par les barycentres, ceux de préfixe J sont les extérieurs (conjugués).
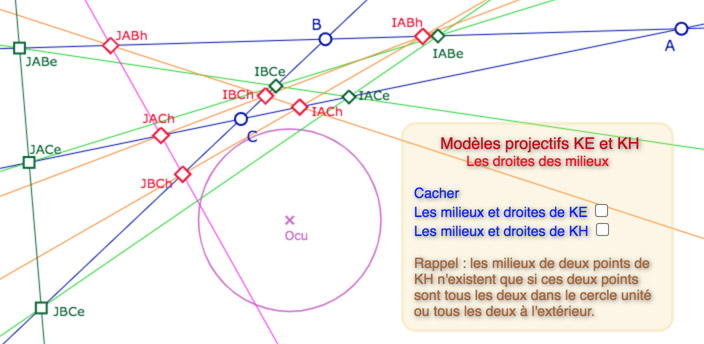
Les 8 droites des milieux, dans KH et KE (quand les milieux existent tous).
Bien-sûr, quand on a déjà pratiqué la géométrie hyperbolique standard, on est un peu surpris de ces quatre KH-droites des milieux mais il ne faut pas oublier qu’il s’agit une approche projective du plongement de KB dans un plan idéal. Voici une illustration dans le cas où les trois sommets \(A, B, C\) sont bien hyperboliques (ie dans KB) :

Les 4 KH-droites de milieux (droites rouges) dans le cas où \(ABC\) est un KB-triangle hyperbolique

Lancer cette figure dans un nouvel onglet
Signalons que cette figure contient déjà 8 macros utilisables pour refaire partiellement ces figures ou en explorer d’autres.
KE et KH Sym correspondent à une symétrie orthogonale.
Rappel : page de présentation de l’utilisation des macros de DGPad.
Retrouver le centre du cercle unité : Quand on utilise un cercle dans une macro (toutes ces macros), cela cache le centre du cercle. Or dans toutes ces figures, c’est très pratique de déplacer le centre du cercle unité pour modifier la figure de manière importante – rapprocher des points hors écran par exemple. Utiliser alors l’icone « gomme » pour pouvoir faire apparaître à nouveau le point.
Les médianes d’un triangle
C’est à partir des médianes que la démarche de Daniel Perrin commence à montrer toute sa pertinence, et toute son efficacité (et ce n’est qu’un début). En effet, montrer que les médianes sont concourantes est vraiment un résultat difficile à obtenir dans le cadre de l’axiomatique de Bachmann, justement parce que les trois géométries (elliptique, euclidienne, hyperbolique) n’étant pas séparées, on ne peut que montrer qu’elles sont en faisceau (avec le vocabulaire des pages des menus) car il y a un cas (un seul) où elles ne sont pas concourantes, dans le cas euclidien sur un corps fini de caractéristique 3, où elles sont parallèles, comme on l’a montré et illustré dans cette page. Bachmann est même amené à faire une preuve spécifique dans chacune des trois géométries. Ici, séparant préalablement le cas euclidien (forme quadratique dégénérée) des deux autres (formes non dégénérées), la preuve de tous les concours de toutes les médianes découle de relations précédemment montrées, simultanément pour les deux géométries, KE et KH (voir page 105).
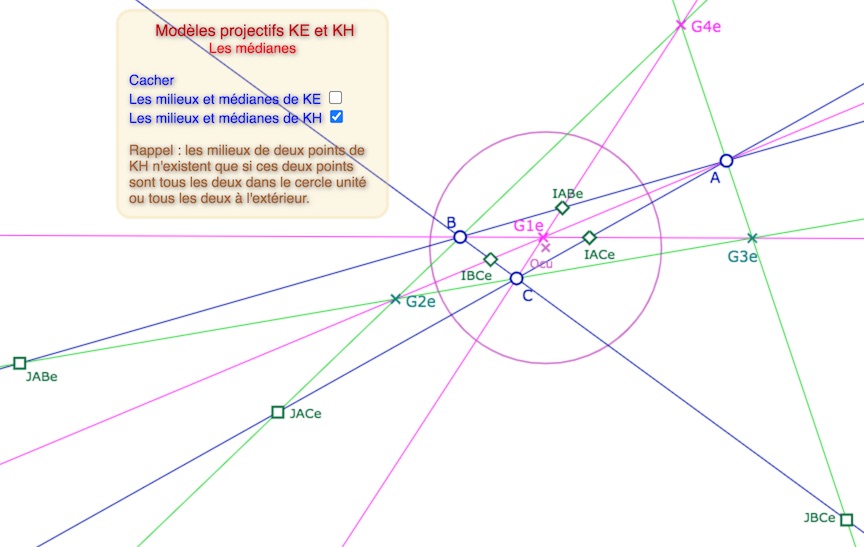
Les 4 KE-médianes et les 4 points d’intersection prises 3 à 3 : \(G1_e, G2_e, G3_e, G4_e\)
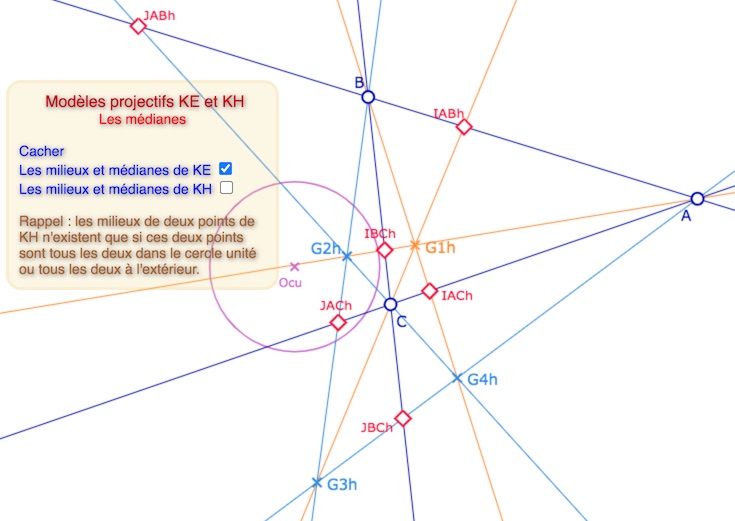
Les 4 KH-médianes et les 4 points d’intersection prises 3 à 3 : \(G1_h, G2_h, G3_h, G4_h\)
Ouvrir cette figure dans un nouvel onglet.
Ne pas hésiter à déplacer le centre du cercle unité et modifier le rayon du cercle, simplement en tirant sur le cercle à la souris.
Bien entendu, comme pour le cas de l’orthocentre, les médianes « ne sont pas concourantes » si l’intersection dans le plan est un point du cercle unité, car c’est un point isotrope. .
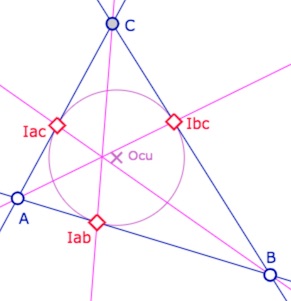
Cas particulier (peut-être réservé à une seconde lecture)
Si une droite \((AB)\) est isotrope, les deux points \(A, B\) ont un seul milieu qui est le point de contact avec le cercle unité (preuve page 96). C’est un des cas de ces « points généralisés » dont on a parlé précédemment, puisque a priori, un tel point n’est pas dans KH (mais est bien dans KE). Et on vérifie aussi qu’il y a toujours concours des médianes.
Ci contre, cas de trois « milieux généralisés », on a pris les tangentes au cercle issues de \(A\), et \(B\) un point sur une de ces tangentes. D’un point de vue euclidien, il s’agit juste de la configuration de Gergonne.
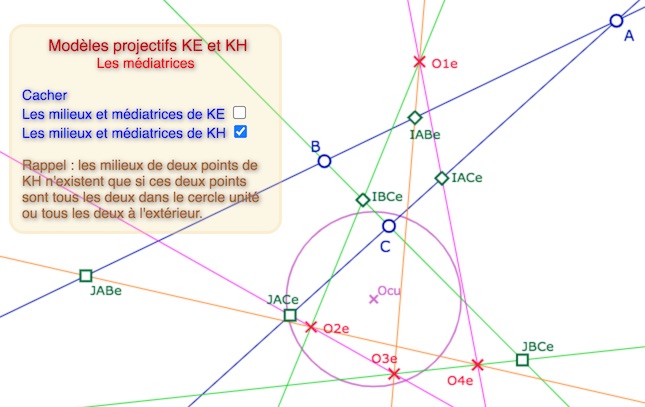
Les médiatrices de deux points
On l’avait déjà exploré dans le modèle elliptique standard, en particulier dans cette page, mais ici, avec le contexte de forme quadratique, il est immédiat (pour des questions de transformations par exemple) que les polaires des milieux de deux points sont les médiatrices de ces mêmes points. Et le fait qu’elles soient trois à trois concourantes est tellement immédiat que Daniel Perrin en profite pour faire un bilan :
Commentaire : Cette démonstration, d’une simplicité enfantine et qui vaut dans un cadre très général puisqu’on ne distingue ni le corps, ni la nature de la géométrie, est significative de ce qu’apportent d’une part l’approche vectorielle, par la possibilité de calcul, et d’autre part la polarité, qui permet de ne faire que la moitié du travail. On notera que la relation qui sous-tend ce résultat est une relation “de Chasles” triviale : (b−c)+(c−a)+(a−b) = 0 que l’on reverra maintes fois.
Daniel Perrin – Partie 4 – p. 102-103
Mais du point de vue des constructions, il faut bien distinguer les deux cas KH et KE car le terme « polaire », s’il a le même sens mathématique indifférencié, ne se traite pas de la même façon comme on l’a déjà vu avec la perpendiculaire commune où nous avons introduit la KE-polaire d’un point. Voyons cela en détail sur les médiatrices de deux points.
Dans l’illustration suivante, la droite rouge passant par \(I_{kh}\) est la polaire (usuelle) de \(J_{kh}\), c’est une KH-médiatrice de \(A\), et \(B\). De même pour l’autre droite rouge. Elles se coupent en \(pAB_{kh}\), le pôle (usuel) de \((AB)\) par rapport au cercle unité.
Par contre, les polaires usuelles de \(I_{ke}\) et \(J_{ke}\), certes vont passer par le pôle de \((AB)\), mais ne passent pas par l’autre KE-milieu et ne sont pas orthogonales (manipulation proposée plus loin) … car ce ne sont pas les polaires elliptique. Il faut en effet utiliser la KE-polaire de \(I_{ke}\), c’est-à-dire la polaire de \(symI_{ke}\). Et bien entendu, elle passe par \(J_{ke}\). De même pour l’autre droite verte. On peut vérifier qu’elles sont orthogonales.
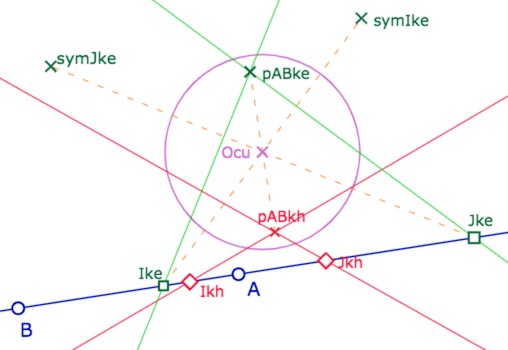
Les KH (rouges) et KE (vertes) médiatrices des deux points \(A\) et \(B\)
Lancer cette figure dans un nouvel onglet pour manipuler la figure, et éventuellement y faire les vérifications proposées ci-dessous. Si nécessaire, (re)lire la page de présentation de l’utilisation des macros.
Pour les personnes non concernées par ces vérifications, on peut aller directement à la section suivante sur les médiatrices d’un triangle.
Les macros de cette figure ont été réorganisées par rapport aux figures précédentes.

Il y deux macros de plus dans KE que dans KH, celles sur le pôle d’une droite et la polaire d’un point. Dans KH on utilisera les macros usuelles du premier niveau. On a aussi ajouté les macros des symétries centrales pour les deux géométries : elles seront nécessaires pour construire les cercles circonscrits à la prochaine section.
Manipulations possibles sur la figure précédente
Vérifications des milieux : comme les macros de symétries centrales sont des constructions géométriques, on peut les utiliser pour « vérifier » la constructions des milieux, qui eux sont calculés à partir des coordonnées des points. Par exemple KE SymC sur \(J_{ke}\) et \(B\) doit donner un point sur \(A\). J’entends bien l’argument qui veut que cela ne vérifie seulement que la macro est correcte.
Quand on a appliqué une macro, on l’annule avant de faire autre chose par la flèche retour à droite du tableau de bord : cela supprime toutes les constructions impliquées dans la macro. On peut aussi relancer la figure initiale en rafraichissant la page.
Vérification de l’orthogonalité des médiatrices entre elles. Par exemple prendre KE Perp sur \(pAB_{ke}\) et une des médiatrices vertes, constater que la macro produit une droite qui recouvre l’autre médiatrice. On peut faire de même avec les KH-médiatrices.
Vérification de l’orthogonalité des médiatrices par rapport à \((AB)\). Même si c’est inutile – si on sait qu’elles passe par le pôle de \((AB)\) pour KH ou le KE-pôle de \((AB)\) pour le cas elliptique, on peut choisir de jouer avec les macros. Par exemple KH Perp sur \(B\) et la médiatrice rouge passant par \(J_{ke}\) doit donner un point sur \(A\).
(KH)-polaire et KE-polaire : c’est la différence entre un raisonnement mathématique où l’on fait des preuves sur les polaires, en général, « sans distinguer la nature de la géométrie » (citation précédente) et la mise en œuvre effective dans le champ des configurations. Même si c’est évident pour le lecteur, on peut s’amuser à le vérifier. Prendre la polaire (du premier niveau des macros) de \(I_{ke}\). Elle ne passe pas par \(J_{ke}\). Puis prendre celle de \(J_{ke}\) et vérifier que les deux ne sont pas KE-orthogonales en prenant la perpendiculaire de l’une passant par leur intersection \(pAB_{kh}\) puissent qu’elle passent par le pôle de \((AB)\).
Les médiatrices d’un triangle
On applique simplement les macros précédentes
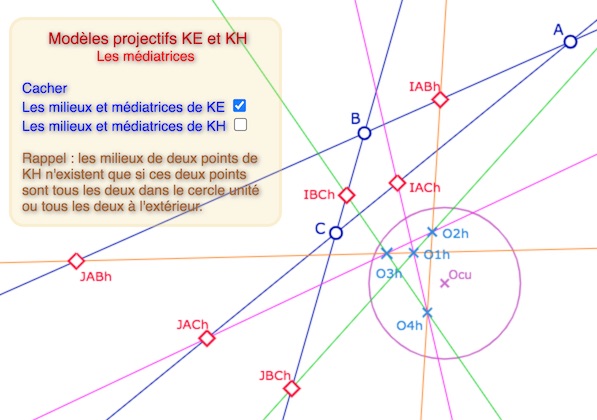
Les KH-médiatrices (ci-dessus) et les 4 KE-médiatrices (ci-dessous) avec les 4 centres des cercles circonscrits associés.
Lancer la figure associée dans un nouvel onglet
Les cercles circonscrits sont construits dans l’article 2a sur les cercles (lien en fin d’article).
Bissectrices et bissecteurs de deux droites
Milieux et médiatrices sont des centres et des axes de symétrie de deux points. On s’intéresse aux centres ou axes de symétries de deux droites. Or comme points et droites sont liés par la polarité, « la question de l’existence des bissectrices de deux droites est équivalente à celles des médiatrices et milieux de leurs pôles » (détails p. 99). C’est à nouveau un exemple de l’efficacité de cette approche des GNE dans un plan projectif muni d’une forme quadratique et de la polarité associée.
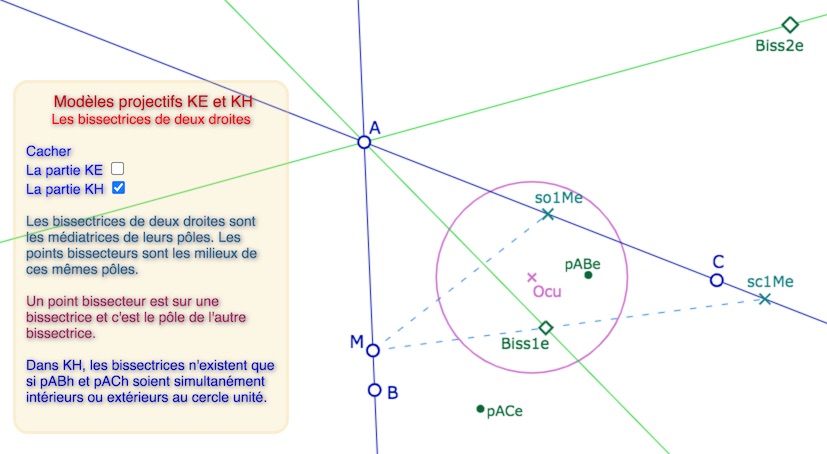
Bissectrices et bissecteurs – Ci-dessus dans KE – Ci-dessous dans KH
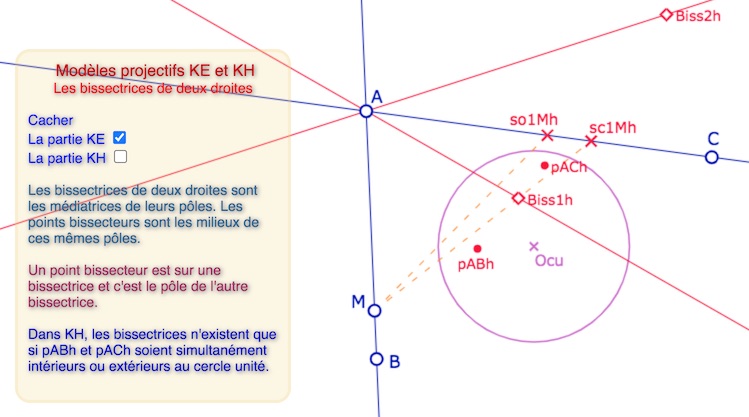
En pratique, dans KH, il n’y a des bissectrices que si les deux droites \((AB)\) et \((AC)\) coupent – ou ne coupent pas – toutes les deux le cercle unité.
Lancer cette figure dans un nouvel onglet. Manipuler le point \(M\), les deux droites et le cercle unité.
Autres manipulations possibles, en utilisant les macros : dans les deux cas on n’a construit qu’un symétrique. On peut prend le symétrique (central ou axial) par rapport au second bissecteur ou à la seconde bissectrice. On verra qu’il coïncide avec un point déjà construit car la seconde bissectrice est la polaire du premier bissecteur et le second bissecteur le pôle de la première bissectrice.
Les cercles inscrits et exinscrits sont construits dans l’article 2a sur les cercles
Les autres articles déjà publiés sur ces modèles
KEKH – 2a – Les cercles (introduction) | KEKH – 2b – Les cercles « paraboles »
KEKH – 3 – Longueur, distance et angles | KEKH – 4 – Spin d’un triangle
Perspectives d’autres publications sur KE-KH
Je souhaiterais surtout – car encore jamais fait – arriver à faire des figures finies dynamiques de cette approche de Daniel Perrin. Je suis preneur de conseils pour le choix du corps fini, par exemple \(\displaystyle \frac{\mathbb{Z}}{7\mathbb{Z}}\) ou \(\displaystyle \frac{\mathbb{Z}}{11\mathbb{Z}}\) sont-ils des bons candidats ? Quelles formes choisir choisir pour KE ? Pour KH ?