Cet article propose d’illustrer la démarche de Hilbert pour reconstruire la géométrie de Bolyaï, sans continuité. En particulier nous allons manipuler plusieurs constructions autour du « corps des extrémités » de Hilbert, qui sera utilisé dans de futures présentations sur la classification des plans de Hilbert. Voici ce qu’en dit Hartshorne, lors de l’introduction du chapitre 41 intitulé « Hilbert’s Arithmetic of Ends » d’un de ses propres ouvrages sur la géométrie.
Nous arrivons maintenant à l’une des plus belles parties de la théorie de la géométrie non euclidienne, qui est une autre illustration de l’utilité de l’algèbre abstraite. C’est le tour de force de Hilbert, que de construire un corps à partir de la géométrie d’un plan hyperbolique. De la même manière que le calcul segmentaire nous a aidé à comprendre la géométrie euclidienne, ce corps nous aidera dans notre étude de la géométrie non-euclidienne. En l’utilisant, nous pouvons prouver des résultats tels que la construction parallèle de Bolyai(*) ou le théorème sur les trois hauteurs d’un triangle. […]. Finalement nous pourrons montrer que le plan hyperbolique est uniquement caractérisé par son corps associé, et est en fait isomorphe au modèle de Poincaré sur ce corps.
(*) il faut entendre « sans hypothèse de continuité »
« Geometry : Euclid and beyond » – Robin Hartshorne – p 388 (3° édition) – Springer
Cet article reprend la démarche et les illustrations telles qu’on les trouve dans l’édition critique de référence de Paul Rossier (Dunod – 1971) sur « les fondements de la géométrie » de Hilbert. On le considèrera comme un modeste hommage au « tour de force » de Hilbert.
Bien entendu les illustrations se font dans le modèle « réel » – donc avec continuité – du disque de Poincaré.
Introduction
On considère un plan de Hilbert, c’est-à-dire une géométrie plane qui reprend les trois premiers groupes d’axiomes : ceux d’incidence (I.1. à I.3 seulement car on reste dans un plan), ceux d’ordre (II.1 à II.4) et les cinq axiomes de congruence (III.1 à III.5). A partir de ce plan général – et des premiers théorèmes qui en découle (existence de perpendiculaires, milieu, médiatrices, symétries orthogonales et centrales, théorèmes de congruence sur les triangles, propriétés des triangles isocèles, bissectrices) – Hilbert ajoute, à la place de l’axiome IV sur les parallèles, un autre axiome IV, d’hyperbolicité, (à rapprocher de l’axiome \( \mathbf{H}\) de Bachmann même si le contexte est différent) dans une démarche proche de celle de Bolyaï, de la façon suivante :
Axiome IV : Soit \(b\) une droite et \(A\) un point qui lui est extérieur. Par \(A\), il passe deux demi-droites \(a_1\) et \(a_2\), qui ne sont pas portées par une unique droite, et qui ne coupe pas la droite \(b\) alors que toute droite intérieure à l’angle formé par \(a_1\) et \(a_2\) coupe \(b\).
Cet axiome est aussi noté Axiome L dans les ouvrages anglo-saxons, comme axiome fondamental de la géométrie de Lobatchevsky.
Cet axiome, associé aux axiomes de congruence, est suffisamment fort pour reconstruire la géométrie hyperbolique plane d’une manière générique.
Hilbert commence par les notations et la définition suivantes :
Partageons la droite \(b\) en deux demi-droites \(b_1\) et \(b_2\) issue de l’un quelconque de ses points \(B\) de telle sorte que \(a_1\) et \(b_1\) soient d’un même côté de la droite \((AB)\), \(a_2\) et \(b_2\) de l’autre. La demi-droite \(a_1\) sera dite parallèle à la demi-droite \(b_1\), et de même \(a_2\) parallèle à \(b_2\), ou encore les deux demi-droites \(a_1\) et \(a_2\) sont parallèles à la droite \(b\).
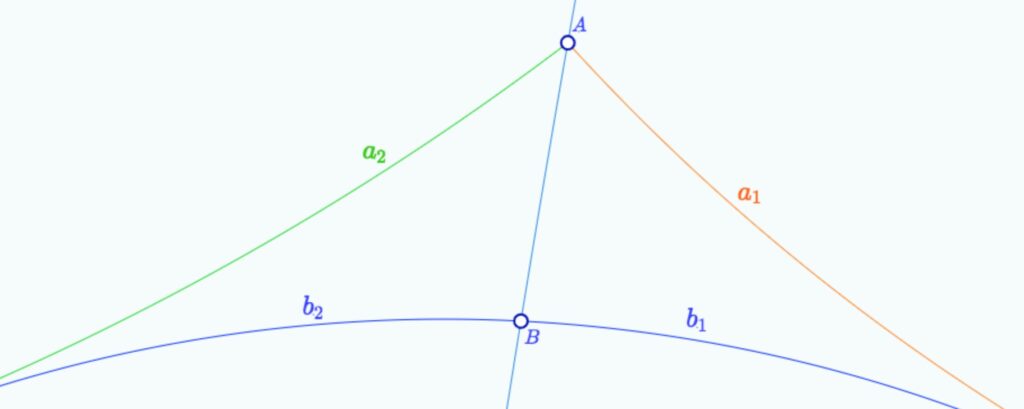
Il poursuit par cette remarque : « De là résulte le fait que si une droite ou une demi-droite est parallèle à une autre droite ou demi-droite, alors la seconde est parallèle à la première ».
Pour la rédaction de son édition critique, l’attention de Mr Rossier a été attirée sur le fait que cette assertion n’est pas aussi évidente que cela. Et donc il la démontre (page 225), ce que nous ne reproduirons pas ici. Enfin Hilbert termine cette introduction par la transitivité des demi-droites parallèles : deux demi-droites parallèles à une même troisième sont parallèles entre elles.
On remarque que cette définition et ces propriétés sont analogues à celles utilisées par Bolyaï.
Les extrémités – Définition
Chaque demi-droite détermine une extrémité. Toutes les demi-droites parallèles entre elles déterminent la même extrémité. On note \((A, \alpha)\) une demi-droite d’origine \(A\) et d’extrémité \(\alpha\). Une droite possède deux extrémités. Nous désignerons par \((\alpha, \beta)\) une droite d’extrémités \(\alpha\) et \(\beta\).
Congruence de figures avec une extrémité
On se donne deux couples de points \((A, B)\) et \((A’, B’)\) ainsi que deux extrémités \(\alpha\) et \(\alpha’\) tels que:
• les segments \([AB]\) et \([A’B’]\) soient congruents
• l’angle de \([AB]\) avec la demi-droite \((A, \alpha)\) soit égal à l’angle de \([A’B’]\) avec la demi droite \((A’, \alpha’)\).
L’angle formé par \([BA]\) et la demi-droite \((B, \alpha)\) est alors égal à l’angle formé par \([B’A’]\) et la demi-droite \((B’, \alpha’)\). On dit que les deux figures \(\mathbf{AB\alpha}\) et \(\mathbf{A’B’\alpha’}\) sont congruentes.
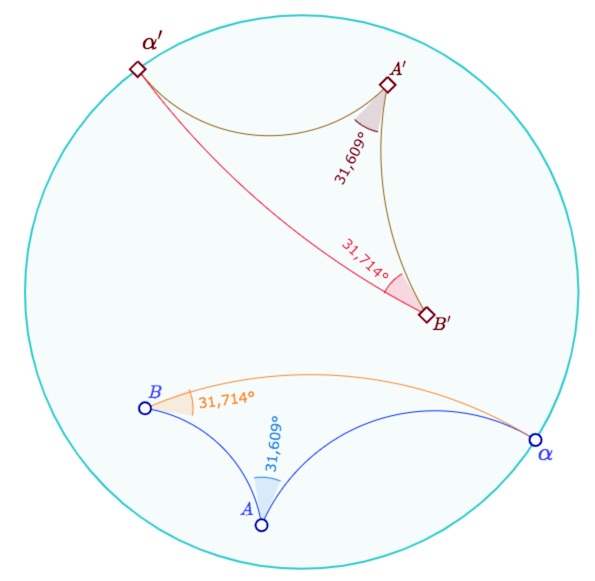
Dans le modèle de Poincaré, les extrémités sont tout simplement les points idéaux sur le cercle horizon.
Rappel : le modèle est conforme, les angles sont ceux des tangentes des arcs de cercles, ici représentés par les mesures entre les tangentes, ce qui explique que les marques ne vont pas jusqu’aux arcs eux-mêmes (à l’origine, pour éviter des lourdeurs de construction dans les figures complexes)
Le mémoire de Hilbert commence alors par une série de 5 lemmes sur les premières propriétés de la géométrie hyperbolique, pour arriver au résultat de la composition de trois symétries orthogonales de droites parallèles qui permet ensuite de définir les opérations du corps des extrémités. Les lecteurs un peu pressés peuvent réserver cette première section à une seconde lecture, même si on y voit comment Hilbert utilise ses axiomes de congruence.
Les lemmes préliminaires
Lemme 1. Si deux droites coupent une troisième en formant des angles alternes congruents, elles ne sont pas parallèles.
Preuve : Supposons que ces deux droites soient parallèles d’un côté. Considérons le milieu du segment coupé par la sécante. Autour de ces points, faisons tourner l’une des droites d’un demi-tour : ceci est réalisable en utilisant un triangle avec extrémité selon la propriété précédente. Alors les deux droites seraient parallèles selon aussi le second ôté, ce qui est exclu par l’axiome IV.
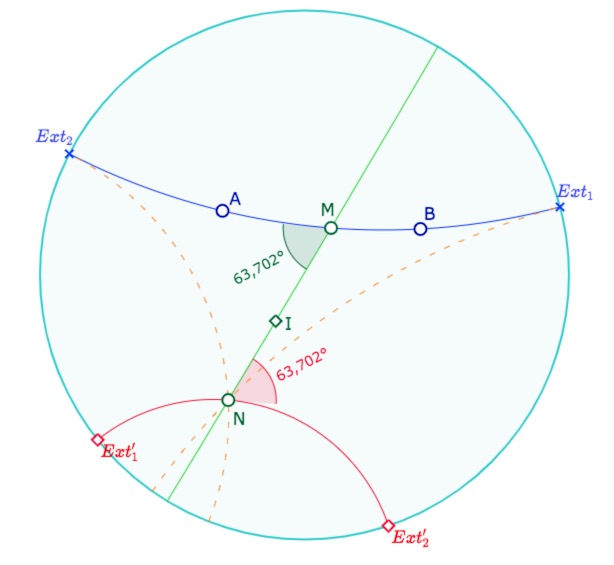
Angles alternes congruents et non parallélisme
Lemme 2 : Il existe une perpendiculaire commune à deux droites non sécantes et non parallèles.
Nous reproduisons la démonstration de Hilbert, illustrée d’une figure dynamique, pour voir l’utilisation forte qu’il fait des axiomes de congruence et d’ordre. Certaines notations sont propres à cette figure, en particulier les extrémités des droites ne sont pas nommées dans la preuve de Hilbert.
Soient donc deux droites \(a\) et \(b\), non sécantes et non parallèles. Dans la figure ci-dessous, on a noté \(a_{\alpha}, a_{\beta}, b_{\alpha}, b_{\beta}\) les extrémités de ces deux droites. De deux points \(A\) et \(P\) de \(a\) on mène les pieds des perpendiculaires à \(b\), respectivement \(B\) et \(B’\) . On se place dans le contexte où \(PB’>AB\), et on construit alors \(A’\), entre \(P\) et \(B’\) tel que \(A’B’=AB\). On construit ensuite la droite \(a’\) (sur l’illustration ci-dessous d’extrémités \(a’_{\alpha}, a’_{\beta}\)) qui passe par \(A’\) et qui coupe \([A’B’]\) en grandeur et en sens avec le même angle que \(a\)coupe \([BA]\) en \(A\). Dans un premier temps, nous allons montrer que \(a’\) coupe \(a\).
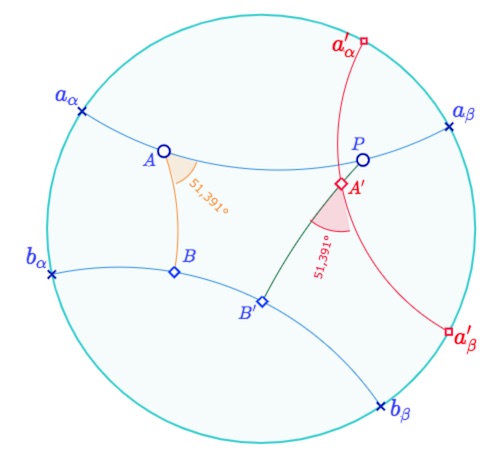
Illustration du préambule à la preuve du lemme 2
Hilbert note ensuite \(a_1\) la demi-droite issue de \(P\), de support \(a\) et qui porte \(A\), c’est-à-dire la demi droite \([Pa_{\alpha})\) ci-dessus tant que \(P\) reste à la droite de \(A\) sur la figure. Par \(B\), menons la demi-droite \(h\) parallèle à \(a_1\). Soit \(h’\) la demi-droite issue de \(B’\) et qui coupe \(B\) selon le même angle que \(h\).

Construction de \(T\). Parallélisme de \(h’\) et \(a’\)
La demi-droite \(h’\) n’est parallèle ni à \(h\) ni à \(a_1\) et elle ne coupe pas \(h\). Par l’axiome IV ci-dessus, elle coupe \(a_1\) en un point \(T\). Par construction, les droites \(h’\) et \(a’\) sont parallèles car les figures \(ABa_{\alpha}\) et \(A’B’a’_{\alpha}\) sont congruentes. Dans l’illustration ci-dessus les extrémités \(h’_{\alpha}\) – verte – et \(a’_{\alpha}\) – rouge – construites indépendamment, sont confondues. Selon l’axiome II.4 (axiome de Pach), la droite \(a’\) coupant le côté \([PB’]\) du triangle \(PB’T\), elle coupe l’autre côté \([PT]\) en un point \(Q\), ce qui prouve la première assertion : les droite \(a\) et \(a’\) sont sécantes.

Fin de la preuve du lemme 2 : construction de \((MN)\), la perpendiculaire commune aux deux droites \(a\) et \(b\)
De ce point \(Q\) on construit la perpendiculaire \((QR)\) sur \(b\), puis le point \(R’\) de \(b\) tel que \(BR’=B’R\), de tel sorte que le sens de \(B\) vers \(R’\) soit celui de \(B’\) vers \(R\). De même, on reporte – point \(Q’\) – la longueur \(A’Q\), à partir de \(A\) sur la droite \(a\), dans le même sens. On appelle \(M\) et \(N\) les milieux de \([QQ’]\) et \([RR’]\). La droite \((MN)\) est la perpendiculaire commune cherchée à \(a\) et \(b\).
En effet, de la congruence des deux quadrilatères \(A’B’QR\) (notation de Hilbert) et \(ABQ’R’\) résulte la congruence des segments [QR][/latex] et \([Q’R’]\) et de la perpendicularité de \((Q’R’)\) sur \(b\), d’où la congruence des quadrilatères \(QRMN\) et \(Q’R’MN\). Le lemme est ainsi démontré.
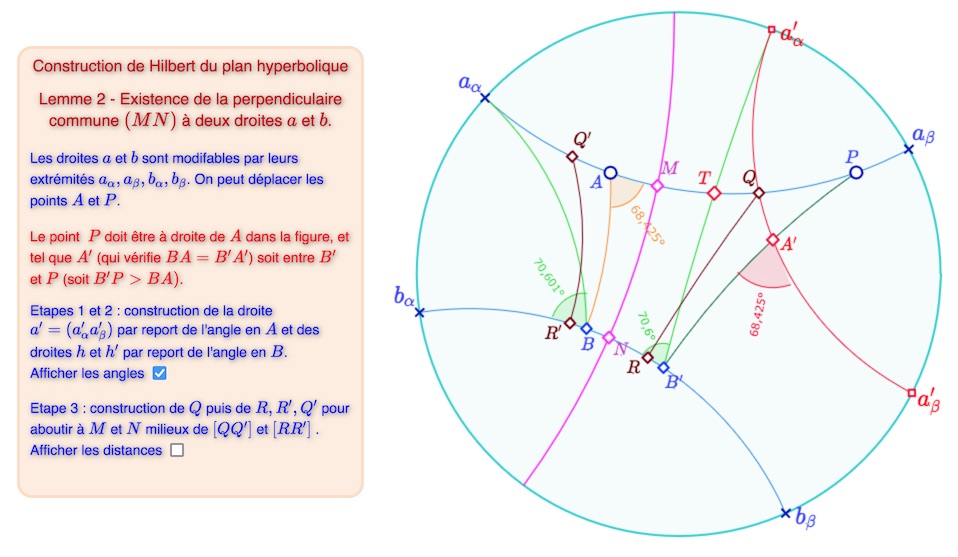
Illustration de la figure finale proposée ci-dessous à la manipulation
Ouvrir la figure complète associée à ce lemme 2 dans un nouvel onglet
Lemme 3. Il existe une droite simultanément parallèles à deux demi-droites données, non parallèles entre elles; ou encore il existe une droite d’extrémités données \(\mathbf{\alpha}\) et \(\mathbf{\beta}\).
Preuve. Il s’agit de montrer que par deux extrémités quelconques \(\alpha\) et \(\beta\) de deux demi-droites, il passe une droite. Voici la démarche de Hilbert.
Par un point \(O\) quelconque, on mène les deux demi-droites \([O\alpha)\) et \([O\beta)\) respectivement parallèles aux deux demi droites données initiales (ci-dessous \([I\alpha)\) et \([J\beta)\). Depuis le point \(O\), on place deux points \(A\) et \(B\) sur chacune de ces deux demi-droites, \(A\) sur \([O\alpha)\) et \(B\) sur \([O\beta)\), tels que \([OA]\) et \([OB]\) soient congruents (\(OAB\) est isocèle en \(O\)). On joint ensuite \(A\) à \(\beta\) et \(B\) à \(\alpha\). Hilbert note ensuite \(a\) et \(b\) les bissectrices des angles \(\alpha A \beta\) et \(\alpha B \beta\). Par construction – voir l’illustration ci-dessous – les configurations \(O A \beta\) et \(O B \alpha\) sont congruentes, on a donc les égalités d’angles \(\angle O A \beta = \ angle O B \alpha\) et donc \(\angle \alpha A \beta = \angle \alpha B \beta \).
La preuve consiste à montrer que ces deux droites \(a\) et \(b\) ne sont ni sécantes ni parallèles, et donc, par le lemme 3, ont une perpendiculaire commune, cette droite ayant alors comme extrémités \(\alpha\) et \(\beta\).
Par construction, les configurations \(O A \beta\) et \(O B \alpha\) sont congruentes, on a donc les égalités d’angles \(\angle O A \beta = \ angle O B \alpha\) et donc \(\angle \alpha A \beta = \angle \alpha B \beta \) .

Illustration du lemme 3
Ouvrir cette figure dans un nouvel onglet
3.1. Les droites \(a\) et \(b\) ne sont pas sécantes.
Supposons que ces deux droites soient sécantes en un point \(M\). De l’égalité des angles \(\angle O A B = \angle O B A\) (triangle isocèle) il en résulte \(\angle B A M = \angle A B M\) et donc \([AM]\) et \([BM]\) sont congruents.
Par \(M\), on mène la demi-droite d’extrémité \(\alpha\). De la congruence des segments précédents et de celle des angles \(\angle \alpha A M\) et \(\angle \alpha B M\), les figures \(\alpha A M\) et \(\alpha B M\) sont congruentes, et cette congruence aurait pour conséquence celle des angles \(\angle \alpha M A\) et \(\angle \alpha M B\), ce qui n’est pas possible. Et donc les droites \(a\) et \(b\) ne sont pas sécantes.
3.2. Les droites \(a\) et \(b\) ne sont pas parallèles.
Si elles l’étaient, elles détermineraient une extrémité \(\mu\). Soient \(C\) l’intersection des demi-droites \([A \beta)\) et \([B \alpha)\) et \(D\) celle de \(a\) avec \([B \alpha)\). Nous allons montrer que si les droites droites \(a\) et \(b\) étaient parallèles alors les segments \([DA]\) et \([DB]\) seraient congruents. Si ce n’était pas le cas, on pourrait reporter \([DA]\) sur \([DB]\) en \([DB’]\). On construit alors la demi-droite \([B’\mu)\). La congruence des figures \(D A \alpha\) et \(D B’\mu\) implique celle des angles \(\angle D A \alpha\) et \(\angle D B’\mu\). Ainsi les angles \(\angle D B’\mu\) et \(\angle D B \mu\) seraient congruents, ce qui est exclu par le lemme 1.
On a donc (sous l’hypothèse \(a\) et \(b\) parallèles) la congruence des segments \([DA]\) et \([DB]\). Celle-ci implique alors celle des angles \(\angle D B A\) et \(\angle D A B\). Mais comme on a déjà la congruence des angles \(\angle C B A\) et \(\angle C A B\), on aurait aussi celle des angles \(\angle D A B\) et \(\angle C A B\), ce qui n’est pas. Ainsi les droites \(a\) et \(b\) ne sont pas parallèles.
3.3. Fin de la démonstration
Les droites \(a\) et \(b\) n’étant ni parallèles ni sécantes, elles ont donc (lemme 2) une perpendiculaire commune \(c\) qui coupe \(a\) et \(b\) respectivement en \(E\) et \(F\). Reste à montrer que les extrémités de cette droite \(c\) sont bien \(\alpha\) et \(\beta\). Pour cela supposons que \(\alpha\) ne soit pas une extrémité de la droite \(c\) . On peut alors construire les demi-droites \([E\alpha)\) et \([F\alpha)\). Or comme les segments \([AE]\) et \([BF]\) sont congruents, les figures \(E A \alpha\) et \(F B \alpha\) sont congruentes, ce qui implique la congruence des angles \(\angle A E \alpha\) et \(\angle B F \alpha\), et alors les angles formés en \(E\) et \(F\) par la droite \(c\) avec les demi-droites \([E\alpha)\) et \([F\alpha)\) seraient eux aussi congruents, ce qui est impossible, d’après le lemme 1. Ainsi le lemme 3 est démontré.
Lemme 4. Soient \(\mathbf{a}\) et \(\mathbf{b}\) deux droites et \(\mathbf{O}\) un point entre \(\mathbf{a}\) et \(\mathbf{b}\). On note \(\mathbf{O_a}\) et \(\mathbf{O_b}\) les symétriques de \(\mathbf{O}\) par rapport à \(\mathbf{a}\) et \(\mathbf{b}\). Soit \(\mathbf{M}\) le milieu de \(\mathbf{[O_a O_b]}\). Alors la demi-droite issue de \(\mathbf{M}\) et parallèle à \(\mathbf{a}\) et \(\mathbf{b}\) est perpendiculaire à \(\mathbf{[O_a O_b]}\).

Preuve : On note \(P\) et \(Q\) les intersections de \([O_a O_b]\) avec les droites \(a\) et \(b\). Comme \(PO<PQ+QO\), on a \(PO_a<PO_b\) et de même \(QO_b<QO_a\), et donc \(M\), comme \(O\), appartient à la région du plan entre les droites \(a\) et \(b\).
Supposons désormais que l’orthogonalité en \(M\) ne soit pas réalisée alors la perpendiculaire à \([O_a O_b]\) en \(M\) coupe \(a\) ou \(b\). On suppose par exemple qu’elle coupe la droite \(a\) en \(A\) (droite grise en pointillés ci-dessus). On a alors simultanément \(AO_a = AO\) (\(A\) sur \(a\)) mais aussi \(AO_a = AO_b\) (\(A\) sur la médiatrice de \([O_a O_b]\)) et donc \(AO_b = AO\), soit \(A\) serait sur \(b\), ce qui contredit l’hypothèse initiale de \(a\) et \(b\) parallèles.
Lemme 5. Soient trois droites \(\mathbf{a, b}\) et \(\mathbf{c}\) ayant toutes la même extrémité \(\mathbf{\alpha}\). On note \(\mathbf{s_a, s_b, s_c}\) les symétrie orthogonales par rapport à ces droites. Alors il existe une droite \(\mathbf{d}\) telle que \(\mathbf{s_c s_b, s_a=s_d}\), et \(\mathbf{d}\) a pour extrémité \(\mathbf{\alpha}\).
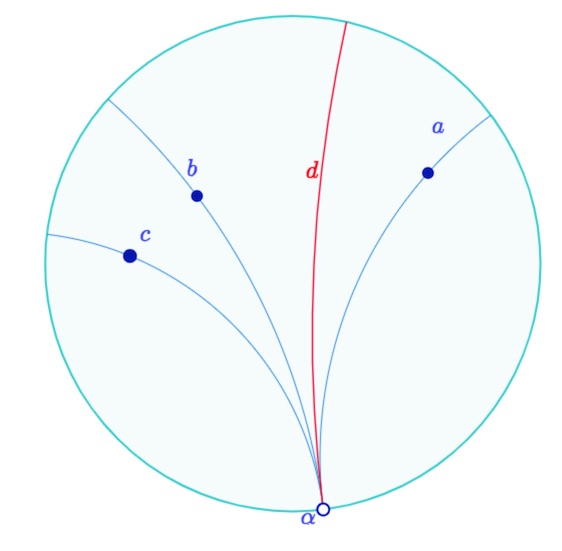
Ouvrir cette figure dans un nouvel onglet (pour tester les cas particuliers abordés plus loin)
Dans l’axiomatique de Bachmann, ce résultat est obtenu, de manière absolue, avant séparation des géométries.
Th 14 : théorème de transitivité
Si \(a \neq b\) et si \(abc\) et \(abu\) sont des droites, alors \(acu\) est aussi une droite.Commentaire sur ce résultat : un des intérêts de ce théorème – et aussi une des forces de cette axiomatique – est sa preuve dans le cas général, en particulier indépendamment du type pinceau, même s’il est « sans support ». Comme c’est le seul cas désormais significatif, nous l’illustrerons dans ce cas ; en pratique dans le cas où\(P_{ab}\) est un pinceau de deux droites parallèles dans le cas hyperbolique.
Pour plus de détails, consulter cette page sur le théorème de Hjelmselv
Il est montré ici, pour le cas hyperbolique, à partir du lemme précédent.
Preuve : On suppose dans un premier temps que la droite \(b\) est entre les droites \(a\) et \(c\). Soit \(O\) un point de \(b\), on construit, comme précédemment, les symétriques \(O_a\) et \(O_c\) de \(O\) prr rapport à \(a\) et \(c\). On note alors \(d\) la droite passant par le milieu de \(O_a\) et \(O_c\) et d’extrémité \(\omega\). On sait alors, par le lemme 4 que latex]O_a[/latex] et \(O_c\) sont symétriques par rapport à latex]d[/latex], et donc que la composée des 4 symétries orthogonales \(s_d s_c s_b s_a\) est l’identité.
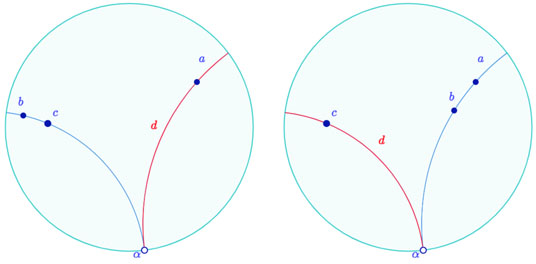
Hilbert poursuit en montrant que le lemme 5 reste valable si \(a=c\) et si c’est \(c\) qui est entre \(a\) et \(b\), de sorte que « la démonstration est ainsi complète. »
Ce lemme acquis, Hilbert aborde la construction des opérations du corps des extrémités.
Addition des extrémités
On se donne deux extrémités, que Hilbert nomme \(0\) (le chiffre) et \(\infty\). Soient \(d\) la droite de ces deux extrémités (lemme 3). Soit \(O\) un point de cette droite. On note alors \(+1\) et \(-1\) les extrémités de la perpendiculaire à \(d\) passant par \(O\).
Définition de l’addition. Soient \(\alpha\) et \(\beta\) deux extrémités autres que \(\infty\). Soient \(O_{\alpha}\) et \(O_{\beta}\) les symétriques de \(O\) par rapport aux droites \((\alpha, \infty)\) et \((\beta, \infty)\). On considère la droite passant par le milieu de \([O_{\alpha}O_{\beta}]\) et d’extrémité \(\infty\). La seconde extrémité de cette droite s’appelle somme des deux extrémités \(\alpha\) et \(\beta\) que l’on nomme \(\alpha+\beta\).
Enfin, l’extrémité de la symétrique par rapport à la droite \((0, \infty)\) d’une demi-droite(*) d’extrémité \(\alpha\) est désigné par \(-\alpha\).
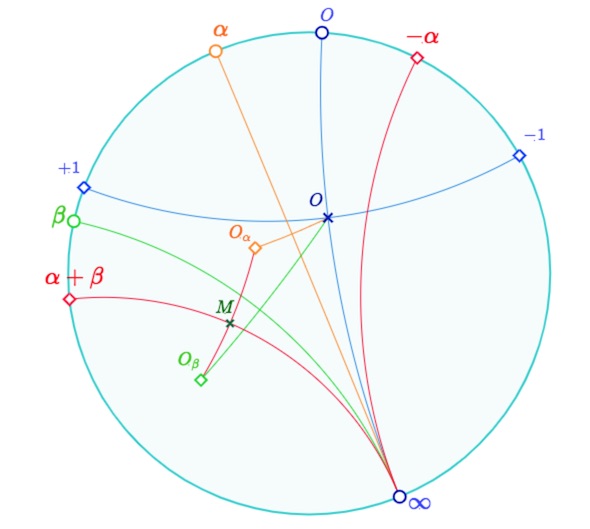
On a alors les relations
\(\alpha + 0 =\alpha\)
\(1+(-1)=0 \quad\) (*) la référence à la demi-droite sert ici
\(\alpha + (-\alpha)=0\)
\(\alpha + \beta = \beta + \alpha\)
Ainsi l’addition des extrémités est commutative
Associativité
On note \(s_x\) la symétrie orthogonale par rapport à la droite d’extrémités \(x\) et \(\infty\) pour \(x= \alpha, \beta, 0\). Alors, par le lemme 5, il existe une droite \((\sigma, \infty)\) telle que \(s_{\sigma}=s_{\beta} \, s_0 \, s_{\alpha}\). Or l’image de \(O_{\alpha}\) par la composition de ces trois symétries est le point \(O_{\beta}\), si bien que \(\sigma =\alpha + \beta\), soit encore \(s_{\alpha + \beta}=s_{\beta} \, s_0 \, s_{\alpha}\).
Soit \(\gamma\) une autre extrémité. En utilisant la relation précédente, on peut écrire :
\(s_{\alpha+(\beta+\gamma)}=s_{(\beta+\gamma)} \, s_0 \, s_{\alpha}=s_{\gamma} \, s_0 \, s_{\beta} \, s_0 \, s_{\alpha}\)
\(s_{(\alpha(\beta)+\gamma}=s_{\gamma} \, s_0 \, s_{(\alpha+\beta)}=s_{\gamma} \, s_0 \, s_{\beta} \, s_0 \, s_{\alpha}\)
On a donc \(s_{\alpha+(\beta+\gamma)}=s_{\alpha+(\beta)+\gamma)}\), soit encore \(\alpha+(\beta+\gamma)=\alpha+(\beta)+\gamma)\).
La somme \(\mathbf{\alpha+\beta}\) est indépendante du point \(\mathbf{O}\)
La relation \(s_{\alpha + \beta}=s_{\beta} \, s_0 \, s_{\alpha}\) montre que la construction de la somme de deux extrémités est indépendante du choix du point \(O\) de la droite \((0 \infty)\). Si \(O’\) est un autre point de la droite, en notant \(O’_{\alpha}\) et \(O’_{\beta}\) les symétriques de \(O’\) par rapport aux droites \((\alpha, \infty)\) et \((\beta, \infty)\), alors la médiatrice de \([O’_{\alpha}O’_{\beta}]\) est la droite \((\alpha+\beta, \infty)\).
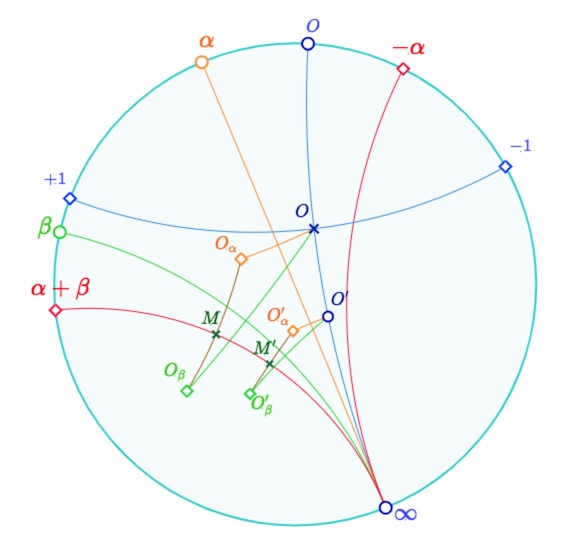
Indépendance de la définition de \(\alpha + \beta\) du point \(O\) sur \((0, \infty)\).
Ouvrir cette figure dans un nouvel onglet.
On peut déplacer \(O’\) pour voir illustrer la propriété, mais en fait déplacer simplement \(O\) aurait suffit à illustrer l’indépendance de la définition par rapport au point \(O\).
Symétrique de \(\mathbf{(\alpha, \infty)}\) par rapport à \(\mathbf{(\beta, \infty)}\)
Soit \(P\) un point de la droite symétrique de \((\alpha, \infty)\) par rapport à la droite \((\beta, \infty)\). Ce point est, par définition, invariant par rapport à la composée \(s_{\beta} \, s_0 \, s_{-\alpha} \, s_0 \, s_{\beta}\). Or la formule précédente montre que \(s_{\beta} \, s_0 \, s_{-\alpha} \, s_0 \, s_{\beta}=s_{2\beta-\alpha} \). Autrement dit cette composée revient à une symétrie par rapport à la droite \((2\beta-\alpha, \infty)\). Le point \(P\) appartient donc à cette droite.
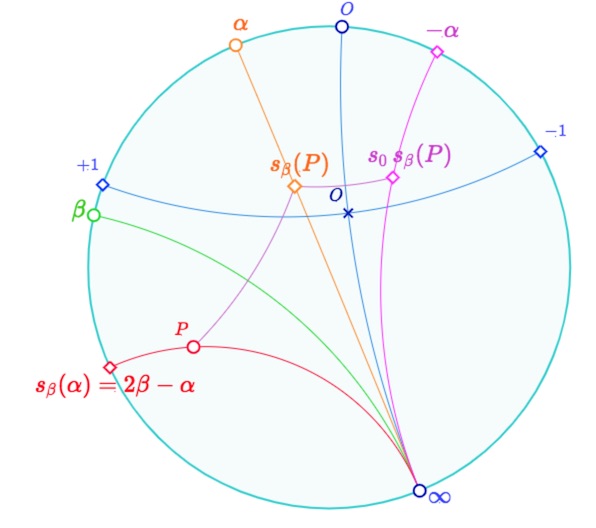
Symétrie orthogonale d’une extrémité par rapport à une droite
Ouvrir cette figure dans un nouvel onglet.
Une conséquence – qui sera utilisée dans la preuve de la partie 4 – est que, pour \(x\) et \(\alpha\) deux extrémités, \(\displaystyle s_{\frac{\alpha}{2}} \, s_0(x)=x+\alpha\).
Multiplication des extrémités
Définition. Une extrémité est dite positive si elle est du même côté de la droite \((0, \infty)\) que l’extrémité \(+1\), et elle est négative si elle est du même côté que l’extrémité \(-1\),
Soient alors \(\alpha\) et \(\beta\) deux extrémités, autres que \(0\) et \(\infty\). Les deux droites \((\alpha, -\alpha)\) et \((\beta, -beta)\) coupent la droite \((0, \infty)\) en \(A\) et \(B\) respectivement. On reporte en \(C\) le segment \([OA]\) depuis \(B\) et dans le même sens que de \(O\) à \(A\). La perpendiculaire à \((0, \infty)\) en \(C\). On appelle produit des deux extrémités \(\alpha\beta\) les deux extrémités de cette droite, « en obéissant à la règle des signes ».
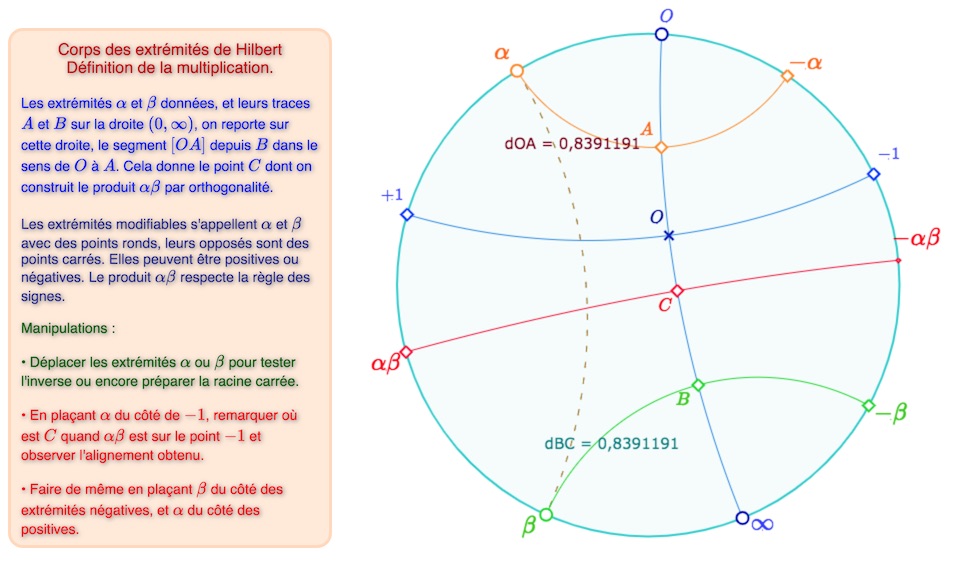
Définition du produit de deux extrémités. Les distances ne sont que des illustrations a posteriori du modèle.
La figure respecte « l’application de l’obéissance à la règle des signe ».
Ouvrir cette figure dans un nouvel onglet
Hilbert pose ensuite, pour la cohérence de la définition, \(\alpha . 0 = 0 . \alpha = 0\). Les axiomes de congruence des segments (les axiomes III.1 à III.3) assurent immédiatement que \(\alpha \beta=\beta \alpha\) et que \(\alpha (\beta \gamma) =(\alpha \beta) \gamma\).
La multiplication des extrémités est donc commutative et associative.
On voit tout de suite que \(1 \, . \, \alpha = \alpha\) et que \((-1) \, \alpha = -\alpha\).
A propos du produit \(\mathbf{\alpha \beta=-1}\)
Si l’équation \(\alpha \beta=-1\) est satisfaite, la droite \((\alpha, \beta)\) passe par \(O\).
Hilbert – Traduction Paul Rossier – Édition critique p 230
Cette propriété, juste mentionnée ici, sera essentielle, dans la dernière partie du mémoire, pour montrer que l’équation tangentielle d’un point est linéaire, c’est la raison pour laquelle nous avons attirer l’attention sur cette propriété dans la manipulation de la figure précédente.
La propriété est immédiate, en anticipant sur le paragraphe suivant : si \(\alpha \beta=-1\) c’est que \(\displaystyle \beta=\frac{-1}{\alpha}\). Or l’inverse est obtenu par la symétrie par rapport à la droite \((+1, -1)\) et l’opposé par la symétrie par rapport à la droite \((0, \infty)\), la composée des deux est la symétrie centrale par rapport au point \(O\) d’où l’alignement entre \(\alpha, O, \beta\) quand \(\alpha \beta=-1\).
Division et racine carrée
L’exposé de Hilbert se poursuit par cette phrase : « La possibilité de la division est immédiate ». Même si c’est immédiat, on peut en rendre compte :
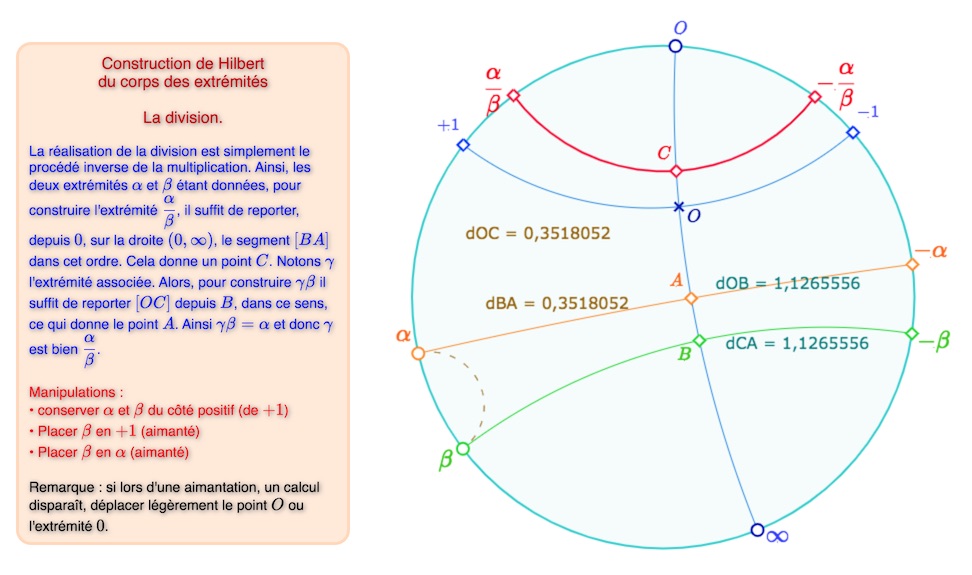
Exploration de la division des extrémités
Ouvrir cette figure dans un nouvel onglet
Pour sortir de l’aimantation des points \(\alpha\) et \(\beta\), il faut tirer rapidement un des deux points. On peut aussi relancer la figure dans le navigateur.
On retiendra aussi que l’inverse d’une extrémité est son symétrique par rapport à la droite \((+1 \, , -1)\)
De même, Hilbert mentionne la possibilité de déterminer la racine carrée … car il aura besoin des deux un peu plus loin dans son développement. La construction est encore plus immédiate.

Et ainsi, le corps des extrémités d’un plan hyperbolique est nécessairement pythagoricien.
Ouvrir cette figure dans un nouvel onglet.
La distributivité de la multiplication par rapport à l’addition
Hilbert la présente de cette façon
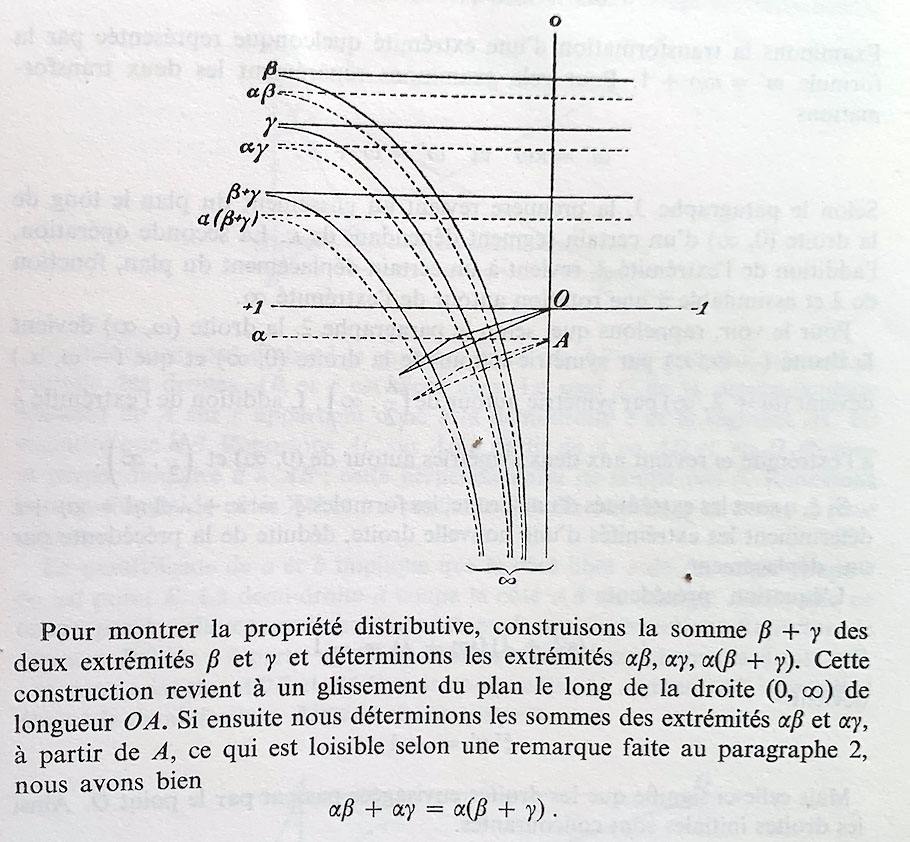
La remarque du paragraphe 2 est l’indépendance de la somme par rapport au point \(O\).
Voici une version dynamique … pour manipuler « le glissement ».
Déplacer les points \(\beta, \gamma, \alpha\) en les laissant du côté des extrémités positives,
Le point \(\alpha\) est légèrement aimanté par le point \(+1\). Les deux triangles sont isométriques.
Précisions sur la construction :
• On a noté \(c_x\) la trace (coordonnée) de l’extrémité \(x\) sur la droite \((0, \infty)\).
• Le point \(c_{\alpha(\beta+\gamma)}\) est construit selon la règle de la multiplication par \(\alpha\) : le segment \([c_{\alpha} \, c_{\alpha(\beta+\gamma)}]\) est congruent à \([O \, c_{\beta+\gamma}]\), dans le même sens. Ce point permet (par perpendiculaire – droite rouge) de construire l’extrémité \(\alpha(\beta+\gamma)\).
• L’extrémité positive de la médiatrice (droite en vert foncé) de \([s_{\alpha\beta}(O) \, s_{\alpha\gamma}(O)]\) est \(\alpha\beta+\alpha\gamma\). C’est le même point que le précédent, par indépendance de la construction par rapport à l’origine. Cette médiatrice est aussi celle de \([s_{\alpha\beta}(A) \,s_{\alpha\gamma}(A)]\) : les deux segments ont dont leur médiatrice commune.
• On peut déplacer (très doucement) les extrémités \(0\) ou \(\infty\) en réajustant à chaque micro-déplacement la position du point \(O\) qui va en général sur l’extrémité \(0\). On peut aussi toujours revenir à la figure initiale en la rechargeant avec l’icone de gauche de l’iframe.
Préférer ouvrir cette figure dans un nouvel onglet (figure plus grande)
En notant \(\mathbf{\mathbb{K}}\) l’ensemble des extrémités autres que \(\mathbf{\infty}\). Alors muni de ces deux opérations \(\mathbf{(\mathbb{K},+, .)}\) est un corps ordonné pythagoricien.
La quatrième et dernière partie du mémoire de Hilbert s’intitule « Equation du point« . Elle est un peu plus technique et aboutit au résultat souhaité par Hilbert : la reconstruction algébrique de la géométrie hyperbolique. Avant de l’aborder, nous nous permettons une petite escapade dynamique pour s’approprier un peu plus le corps des extrémités de Hilbert, juste pour le plaisir de faire de belles figures.
Escapade dans le corps des extrémités
Commençons par placer les extrémités qui correspondent aux entiers. Pour cela on utilise la relation montrée plus haut \(s_{\beta}(\alpha)=2\beta – \alpha\), où \(s_{\beta}\) est la symétrie orthogonale par rapport à la droite \((\beta \, \infty)\). On commence par l’appliquer à \(+1\) et \(0\) : \(2=s_1(0)\), puis \(3=s_1(1)\), et on poursuit, avec parfois de nombreuses possibilités comme \(8=s_4(0)=s_5(2)=s_6(4)=s_7(6)\).
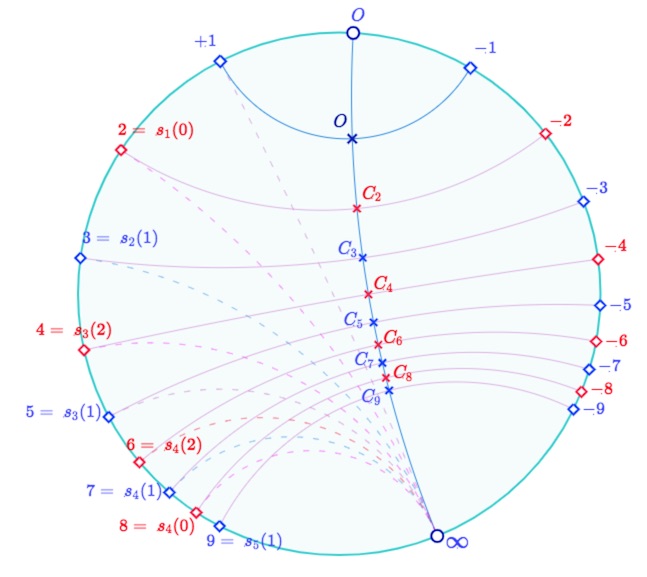
Construction des premiers entiers par symétrie orthogonale
On nomme \(C_k\) l’intersection de la droite \((k, \, -k)\) avec la droite \((0 \,\infty)\), pour \(k=2, 3,… 9\). Alors par définition même de la multiplication, puisque \(6=2 \times 3\), \(8=2 \times 4\), \(9=3 \times 3\), on a \(OC_2+OC_3=OC_6, OC_2+OC_4=OC_8\) et \(2OC_3=OC_9\). En notant \(d(k)=OC_k\), ces relations s’écrivent \(d(2)+d(3)=d(6), d(2)+d(4)=d(8)\) ou encore \(2d(3)=d(9)\), et plus généralement \(d(x)+d(y)=d(xy)\), pour les entiers d’abord puis pour tous les éléments du corps des extrémités. On donc donc un morphisme de groupe additif sur le groupe multiplicatif : on ne sera donc pas surpris de l’illustration suivante qui contient, en plus, la continuité.
Expression de la valeur numérique d’une extrémité
On peut alors aller un peu plus loin comme dans cette figure
Préférer ouvrir cette figure dans un nouvel onglet (figure plus grande).
Robin Hartshorne donne cette définition

Pour utiliser le logarithme comme dans la figure, on doit se placer dans la situation où le corps des extrémités est un sous-corps de \(\mathbb{R}\), comme dans ces deux exercices :

Autre illustration
On peut s’amuser à regarder une autre façon de construire les entiers par l’action naturelle de \(\mathbb{Z}\) sur \(\mathbb{K}\) … en utilisant par exemple que \(\displaystyle 2 = \frac{\alpha+\alpha}{\alpha}\) … juste pour le plaisir de jouer.
Préférer ouvrir cette figure dans un nouvel onglet
Équation du point
Nous reprenons l’exposé de Hilbert. Le corps des extrémités va permettre à Hilbert de définir les équations tangentielles des points ce qui lui permet de retrouver son approche algébrique (développée dans un chapitre précédent sur le calcul segmentaire) et conclure rapidement. Si nous présentons les définition de Hilbert, les illustrations proposées seront associées à la présentation qu’en fait Hartshorne, qui est à la fois plus simple et plus précise.
Coordonnées d’une droite
Soient \(\xi\) et \(\eta\) les extrémités d’une droite. Les extrémités \(u=\xi \eta\) et \(v= \displaystyle \frac{\xi + \eta}{2}\) sont appelées les coordonnées de cette droite.
Équation tangentielle d’un point
Soient \(\alpha, \beta, \gamma\) trois extrémités telles que l’extrémité \(4 \alpha \gamma – \beta^2\), est positive, Toutes les droites dont les coordonnées \(u, v\) satisfont à l’équation \(\alpha u + \beta v + \gamma = 0\) passent par un même point.
Pour démontrer ce résultat, Hilbert est amené à faire une changement de variable qui, géométriquement, reste délicat (dynamiquement parlant) à mettre en place : il suppose acquises les constructions de \(\displaystyle \kappa = \frac{2\alpha}{\sqrt{4\alpha\gamma – \beta^2}}\) et \(\displaystyle \lambda = \frac{\beta}{\sqrt{4\alpha\gamma – \beta^2}}\).
Robin Hartshorne propose une variante bien plus abordable. Tout d’abord il garde les extrémités comme « coordonnées » des droites, puis il montre le résultat suivant :

Équation tangentielle de points – Hartshorne – p. 394
D’une part, il n’y a que deux variables, les extrémités \(a\) et \(b\), au lieu des trois \(\alpha, \beta, \gamma\) de Hilbert. Et de plus on a très facilement le point décrit par cette équation tangentielle, comme indiqué ci-dessous :

Ceci est analogue à la géométrie analytique ordinaire, mais les détails sont tous différents, ayant
« subi une transformation radicale en quelque chose de riche et d’étrange ».
Hartshorne (introduction au chapitre 41) – La citation entre guillemets est de Hilbert.
Mise en œuvre dynamique de cette propriété
On se propose de faire une figure la plus générale possible. Pour cela, on se donne d’abord un point \(P\), manipulable, ce qui donne les extrémités \(a\), positive, et \(b\), qui peut être négative. On se donne ensuite un point \(M\) que l’on pourra faire « tourner » autour de \(P\). La droite \((MP)\) a pour extrémités, celles du théorème \(u_1, u_2\). La figure consiste à illustrer que, pour \(P\) donné, manipuler \(M\) autour de \(P\) laisse l’expression \(u_1u_2-b(u_1+u_2)+a^2\) nulle. Et plus précisément, pour éviter d’avoir une ultime médiatrice confondue avec la droite \((0, \infty)\), on va plutôt construire l’expression \(u_1u_2-b(u_1+u_2)\) et vérifier qu’elle coïncide avec l’extrémité \(-a^2\).
La preuve de Hilbert (reprise par Harstshorne) consiste a faire un changement de variable pour que le point dont il est question, le point \(P\), soit envoyé sur le point \(O\). Les droites initiales ainsi transformées vérifient (par exemple chez Hilbert) \(\xi’\eta’=-1\) donc, d’après une remarque initiale présentée à propos de la multiplication, cette droite passe par O. Ainsi toutes les droites passent par \(P\).
Précisions techniques de réalisation
Pour ne pas alourdir la présentation de la multiplication, nous n’avions pas détaillé la mise en œuvre dynamique de « l’application de l’obéissance à la règle des signe », pour reprendre l’expression de Hilbert. On le fait sur cette figure, mais c’est toujours le même principe. Le produit \(u_1u_2\) est programmé pour rendre compte de toutes les possibilités de signe : en déplaçant \(M\) ou \(P\), on peut placer le produit \(u_1u_2\) sur \(-1\) alors la droite \((u_1, \,u_2)\) passe par \(O\).
Pour réaliser cela, une première variable \(u_1u_2P\) dit si le produit est positif. Ensuite, le produit prend l’un des deux extrémités \(P_{60}\) ou \(P_{51}\) de la droite portant le produit. L’expression peut paraître artificiellement lourde, mais cela résulte du fait que ces deux extrémités sont elles-mêmes échangées quand l’orientation de la droite change par rapport au cercle horizon : quand l’arc de cercle traverse le centre du disque de Poincaré les points \(P_{60}\) et \(P_{51}\) sont échangés, d’où les précautions prises.

Illustration que la droite \((MN)\) passe par \(O\) ssi \(u_1u_2=-1\).
La figure dynamique
La droite bleue est la médiatrice de \(s_{u_1u_2}(O) \, s_{-b(u_1+u_2)}(O)\). Elle a pour extrémités \(\infty\) et \(u_1u_2-b(u_1+u_2)\), qui coïncide avec \(-a^2\), ce qui montre que l’équation tangentielle du point est vérifiée, indépendamment du point M (et donc vérifié pour tout couple d’extrémité \((u_1, u_2)\).
Dans cette figure, on peut :
• Manipuler \(M\)
• Déplacer \(P\) qui peut être placé dans le demi-plan contenant les extrémités négatives.
• Dans ce cas (\(P\) du côté de \(-1\)) alors éviter que la somme \(u_1+u_2\) soit négative, la figure devient instable : en déplaçant \(M\), faire en sorte que \(u_1+u_2\) soit du même côté que \(+1\) par rapport à la droite \((0, \infty)\).
Préférer ouvrir cette figure (avec d’autres commentaires) dans un nouvel onglet.
Remarque : en pratique la condition \(|b|<a\) est toujours vérifiée.
Fin du mémoire de Hilbert
Les dernières lignes du mémoire concluent alors
Nous venons de voir que l’équation tangentielle d’un point est linéaire. On en déduit la validité du théorème spécial de Pascal (théorème 40) pour la paire de droites, celui de Desargues (théorème 53) pour les triangles perspectifs ainsi que les théorème de géométrie projective. De là, on déduit les formules connues de la géométrie lobatchevskienne, et l’élaboration de celle-ci est ainsi possible sur la base des axiomes (I) à (IV).
Hilbert – ‘Fondements » – Traduction de Paul Possier – p 232
La présentation de Hartshorne et ses compléments
Hartshorne est plus détaillé dans son développement, il prend le temps de définir la tangente d’un angle sous forme d’une extrémité puis montre la formule de Bolyaï sur l’angle de parallélisme, bien entendu sans exponentielle, mais avec la mesure \(\mu\) comme mentionnée dans sa proposition 41.7 citée plus haut. Il montre la construction de Bolyaï de la parallèle à une droite (dans une direction), ceci sans cercle. Cette preuve a la particularité d’utiliser l’axiome IV de Hilbert, c’est-à-dire le fait de savoir que cette parallèle que l’on veut construire existe a priori. Il précise même, dans des exercices, que sans cela la construction peut donner des droites non parallèles (dans des corps non archimédiens).
Deux chapitres plus loin, comme annoncé dans l’introduction du chapitre 41, il montre que le corps des extrémités est caractéristique du plan hyperbolique :
La preuve utilise à nouveau les équations tangentielles de points. Et il en déduit ce corollaire remarquable … obtenu grâce au « tour de force » de Hilbert …

Cet article sera suivi d’autres, sur des thèmes proches, en particulier autour de la classification des plans de Hilbert par Pejas, élève de Bachmann.