Dans différentes pages des menus, celle sur les pavages dans DP, mais aussi dans plusieurs pages du menu PSH, sur les pavages (comme P54_P45 ou P38_P83 entre autres) on a plusieurs fois renvoyé à un futur article sur les constructions préliminaires aux pavages : la construction des cercles de pavage.
[latexpage]
Quel type de construction ?
Chaque activité particulière induit ses problématiques spécifiques. Pour un site de géométrie, qui plus est sur les GNE, la réalisation des figures questionne régulièrement les choix retenus pour les constructions. Essaie-t-on de réaliser une construction géométrique – typiquement « règle et compas », éventuellement intersection de coniques- où choisi-t-on une construction plus analytique ? C’est pour aborder cette question sur les cercles de pavages avec un peu plus de recul que l’on présente cette page après avoir illustré le mémoire de Bolyaï , dont on rappelle qu’il a été le premier à s’être questionné sur la constructibilité, au sens de Gauss – des segments en géométrie hyperbolique.
Nous avons illustré le travail de Bolyaï sur deux articles, le premier, accès sur les horicycles et les horisphères se termine sur les formules trigonométriques dans un triangle hyperbolique. Le second aborde la caractérisation des segments constructibles pour montrer la quadrature du cercle. Après avoir proposé une construction géométrique pour un cercle d’aire \(\pi\), Bolyaï,concluait à la quadrature « sous l’hypothèse de la fausseté de l’axiome XI » en calculant le rayon du carré d’aire \(\pi\), montrant en même temps qu’il est constructible. L’article se termine en remarquant qu’il ne propose pas de construction du carré correspondant comme il l’a fait du cercle.
Ayant un critère de constructibilité, on peut se poser la question de savoir si on construit – pour les cas constructibles – un cercle de pavage de manière géométrique ou plus simplement de manière analytique avec les formules des angles de parallélisme par exemple …
Calcul des rayons des cercles de pavage constructibles
On reprend certaines notations de Bolyaï : on préfixe ainsi, comme lui, de \(\Sigma\) la constructibilité euclidienne et de \(S\) la constructibilité hyperbolique. Les résultats du mémoire de Bolyaï sont alors les suivants :
• Les angles sont \(S\)-constructibles si et seulement si ils sont \(\Sigma\)-constructibles.
• Un segment \(r\) est \(S\)-constructible si et seulement si \(sh(r)\) est \(\Sigma\)-constructible, ce qui est équivalent à \(ch(r)\) ou \(e^r\) sont \(\Sigma\)-constructibles.
Décomposition du polygone de P(n,k)
Le pavage \(P(n,k)\) est constitué de polygones réguliers (convexes) à \(n\) côtés tel qu’autour de chaque sommet il y a \(k\) tels polygones identiques. On a déjà montré dans cette page d’introduction aux pavages, qu’un pavage \(P(n,k)\) existe si et seulement si \(\displaystyle \frac{1}{n}+\frac{1}{k}<\frac{1}{2}\).
Un polygone de \(P(n,k)\) a pour angle au centre \(\displaystyle \frac{2\pi}{n}\) et pour angle au sommet \(\displaystyle \frac{2\pi}{k}\). Il est donc composé de \(n\) triangles isocèles de même angle au sommet et d’angle à la base \(\displaystyle \frac{\pi}{k}\). On reprend la démarche de Bolyaï en décomposant ce triangle isocèle en deux triangles rectangles d’angles \(\displaystyle \frac{\pi}{n}\) et \(\displaystyle \frac{\pi}{k}\).
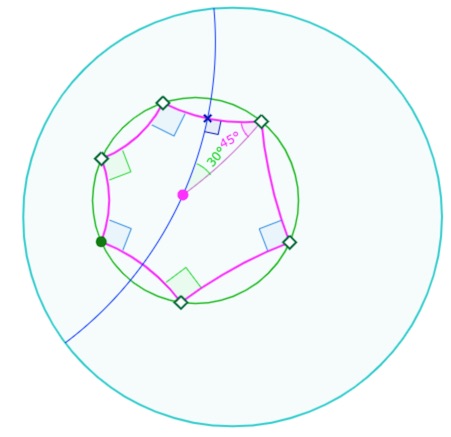
Exemple d’un hexagone \((n=6)\) orthogonal \((k=4)\).
On s’intéresse au triangle rectangle d’angles 30° et 45°.
Calcul du rayon de pavage
On rappelle les résultats trigonométriques déjà vus
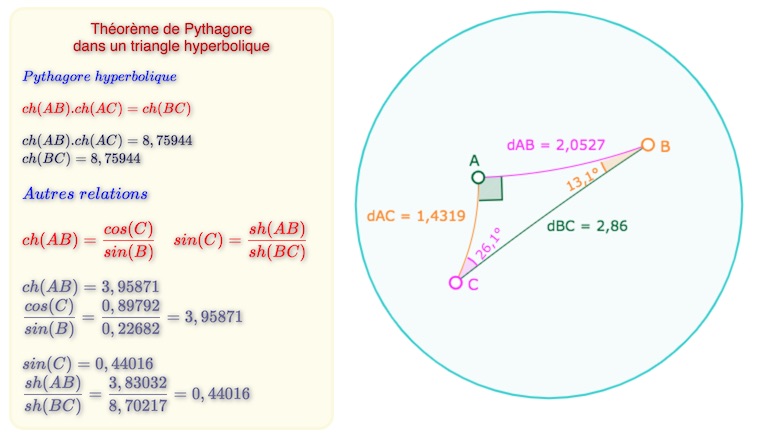
Et donc en notant \(r_{nk}\) le rayon du cercle de pavage de \(P(n,k)\) et \(ch_{nk}=ch(r_{nk})\) on a \(ch_{nk}=\displaystyle cotan \left( \frac{\pi}{n} \right) \; cotan \left( \frac{\pi}{k} \right)\), ce qui, pour \(n\) égal à 4, se simplifie en \(ch_{4k}=\displaystyle cotan \left( \frac{\pi}{k} \right)\). Une première conséquence est que les rayons des cercles de pavage de \(P(n,k)\) et de \(P(k,n)\) sont égaux.
On a donc, pour les premiers angles constructibles usuels :
\(ch_{45} = \displaystyle \frac{4}{(\sqrt{5}-1) \sqrt{2(5-\sqrt{5})}}\), \( \quad ch_{46} =\sqrt{3} \quad\) et \(\quad ch_{48} = \sqrt{\displaystyle \frac{2+\sqrt{2}}{2-\sqrt{2}}} =1+\sqrt{2} \).
mais aussi
\(ch_{38} = \displaystyle \frac{1}{\sqrt{6}- \sqrt{3}}\), \(\quad ch_{55} = \displaystyle 1+2 \frac{\sqrt{5}}{5}\), \(\quad ch_{56} = \displaystyle \frac{\sqrt{3}}{\sqrt{5-2 \sqrt{5}}}\), \( \quad ch_{66} =3 \).
Toutes ces valeurs sont \(\Sigma\)-constructibles, et donc les rayons \(r_{nk}\) des cercles de pavages correspondants sont bien \(S\)-constructibles.
Construction géométrique
d’un cercle de pavage générique Cnk
Tout d’abord, les calculs précédents sont généraux, hyperboliques, indépendants du modèle dans lequel on va représenter la géométrie hyperbolique. Dans un modèle, on ne va pas reconstruire « à la règle et au compas » ce qui est connu comme constructible, on utilisera les expressions directement. Mais on s’assure de n’utiliser que des étapes, à chaque fois, constructibles. On travaille dans le disque de Poincaré. Pour les angles hyperboliques, il n’y a pas de problème, le modèle est conforme.
Pour construire le cercle de pavage \(C_{nk}\) de centre un point \(O\), on va commencer par construire le rayon – la longueur – \(r_{nk}\) depuis le centre du cercle horizon car on sait que les droites sont alors des diamètres du cercle, et on va pouvoir – dans ce cas – exprimer facilement \(r_{nk}\) depuis \(ch(r_{nk})\). Ensuite une symétrie orthogonale hyperbolique par rapport à la médiatrice du centre du cercle horizon et du point \(O\) achèvera la construction. Voici le détail du calcul de \(r_{nk}\) sur un diamètre du cercle, dans le cas où il est de rayon unité.
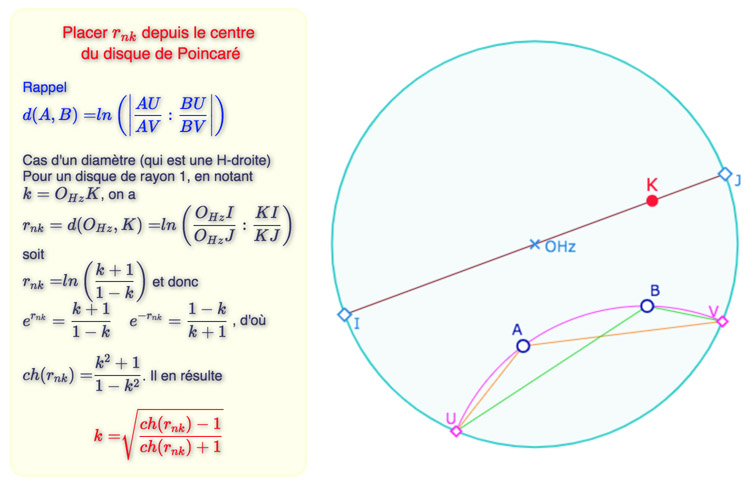
Puisque \(k\) est constructible dès que \(ch_{nk}\) l’est, le rayon \(r_{nk}\) du cercle de pavage de \(P(n,k)\) est bien constructible dans le modèle du disque de Poincaré.
Reste un dernier point, celui de la médiatrice entre un point et le centre du cercle horizon. En effet, la construction standard ne peut s’appliquer car on ne peut prendre l’inverse du centre d’un cercle par rapport à ce cercle. Nous avons déjà utilisé une macro spécifique, mais un peu gourmande en objets intermédiaires que l’on se propose, à l’occasion, d’optimiser – donc en la rendant peut-être un peu ésotérique, construction réalisée « manuellement » et plutôt calculatoire que géométrique, en remplaçant les inversions par le calcul algébrique associé, en restant toujours constructible bien entendu. L’objectif sous-jacent est de rendre la construction du cercle de pavage la plus fluide possible pour que l’on puisse passer d’un pavage à l’autre par un pop-up ou un simple curseur. Le lecteur non concerné peut zapper la partie technique suivante, qui est peut-être aussi, simplement, une mémorisation personnelle placée en lieu sûr (sur le net) …
Dans l’illustration suivante, le point \(T_{nk}\) est la position sur le rayon \(O_{Hz}U_{Hz}\) du point d’abscisse \(t_{nk}\) (le \(k\) de ci-dessus) rapport à un cercle horizon de rayon quelconque. Ensuite
• \(mInvO\) est le milieu entre \(O\) et son inverse par rapport au cercle horizon.
• \(mAA\) est le milieu entre le centre \(O_{Hz}\) et son inverse par rapport au cercle de centre \(mInvO\) passant par \(O\).
• \(P_1\) et \(P_2\) sont les intersections des cercles de centre \(O_{Hz}\) passant par \(O\) et de centre \(mAA\) passant par \(O_{Hz}\). Alors la droite hyperbolique \((P_1P_2)\) est la médiatrice cherchée, de \(O_{Hz}\) et \(O\). Son centre euclidien est le point \(o_{AB}\) (calculé). Alors l’inverse \(A_{nk}\), du point \(T_{nk}\), par ce cercle (non tracé, inverse aussi calculé) est un point du cercle de pavage, qui est donc le cercle hyperbolique de centre \(O\) passant par \(A_{nk}\), de centre euclidien \(Ce_{nk}\).
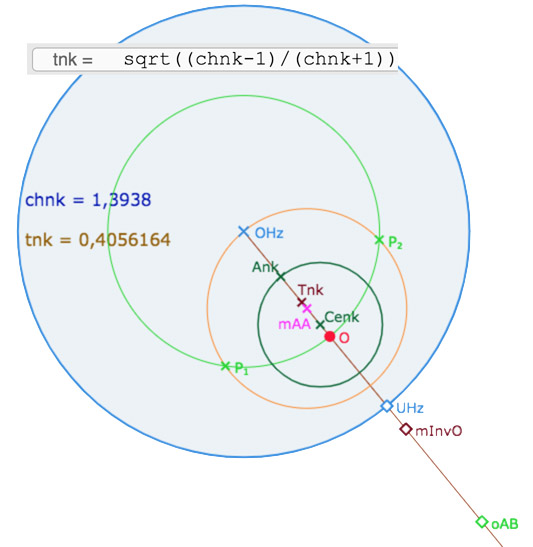
Ci-dessus : construction optimisée du cercle de pavage
Ci-dessous : code de la macro associée

Voyons maintenant quelques premières applications.
La suite de l’article contient trois figures assez lourdes, car il y a plusieurs pavages dans une même figure. Ne pas hésiter à recharger la figure par l’icone de recharge (à gauche), en général il faut cliquer 2 fois. On peut aussi les ouvrir dans un nouvel onglet.
Les pavages P(6,4) , P(6,5) et P(6, 6)
dans une même figure
Préférer ouvrir cette figure dans un nouvel onglet
Les pavages P(5,4), P(5,5) et P(5,6)
dans la même figure
Préférer ouvrir cette figure dans un nouvel onglet
Construction du cercle de pavage
par angle de parallélisme
Préférer ouvrir cette figure dans un nouvel onglet
Quatre pavages dans une même figure
P(8,3), P(8,4), P(8,5), et P(8,6)
On poursuit avec d’autres pavages constructibles. On a :
\(ch_{83}=ch_{38}, \; ch_{84}=ch_{48},\) puis
\(ch_{85}=\displaystyle \frac{\sqrt{5}+1}{\sqrt{2}\sqrt{5-\sqrt{5}}\sqrt{3-2\sqrt{2}}}\) et \(ch_{86}=\displaystyle \frac{\sqrt{3}}{\sqrt{3-2\sqrt{2}}}\)
Penser à déplacer le centre du cercle pendant l’animation (et changer le pavage)
Remarquer – comme dans les autres figures – l’accélération de l’animation
quand le point de référence se rapproche du cercle horizon.
Préférer ouvrir cette figure dans un nouvel onglet
On aurait pu poursuivre par des pavages « non constructibles », mais la page est déjà assez lourde. Se fera dans un autre article.
Autre type de pavages : les pavages non réguliers orthogonaux.