On déjà vu, dans la page d’introduction à l’orthogonalité du modèle de Hilbert que des triangles, en particulier ayant deux sommets dans l’ellipse, peuvent avoir des hauteurs parallèles. Puis nous sommes allés plus loin, dans cette autre page, pour trouver des triangles ayant à la fois deux hauteurs parallèles, et en même temps un orthocentre. Toutefois, dans ces deux situations, nous obtenions les configurations voulues par programmation, avec une manipulation dynamique possible dans le premier, mais pas dans le second cas. C’est ce que l’on se propose d’améliorer.
Dans cet article, on se donne deux droites parallèles, et on se propose de construire des triangles ayant ces deux droites comme hauteurs. Il n’y aura donc plus de programmation pour obtenir ce premier parallélisme, il est donné a priori.
Situation de départ – Notations
Une première droite est définie par une poignée, nommée \(Pgn\) et un point \(A\), que l’on prend à l’intérieur de l’ellipse. C’est la droite verte ci-dessous. Puis, depuis un point \(B\), lui aussi intérieur à l’ellipse, on construit la parallèle à cette première droite passant par ce point, c’est la droite orange ci-dessous.
A partir de ces deux points \(A\) et \(B\), on se propose de chercher les points \(C\) tels que le triangle \(ABC\) ait ces deux droites parallèles comme hauteurs, une issue de \(A\) et l’autre de \(B\).

Les trois points possibles \(C_{hh}, C_{he}, C_{eh}\) pour un troisième sommet \(C\) du triangle \(ABC\).
Notations de la figure
On note \(hA_h\) le pied de la perpendiculaire à la droite initiale verte issue de \(B\) : \(hA_h\) et non pas \(hB_h\) comme on pourrait le penser, car, dans le triangle à construire, ce sera le pied de la hauteur issue de \(A\) sur la droite \((BC)\). De même le pied de la perpendiculaire à la parallèle (orange) issue de \(A\) est noté \(hB_h\) car ce sera le pied de la hauteur issue de \(B\) sur la droite \((AC)\). De \(B\), il existe une autre perpendiculaire à la droite verte, de pied \(hA_e\), le suffixe \(h\) pour préciser une perpendiculaire hilbertienne et \(e\) pour une perpendiculaire euclidienne. Le point \(hA_e\) est le pied de la hauteur issue de \(A\) sur une autre droite \((BC)\).
On note alors \(C_{hh}\) l’intersection des droites \((B \, hA_h)\) et \((A \, hB_h)\), et de même \(C_{eh}\) celle des droites \((B \, hA_e)\) et \((A \, hB_h)\).
Quand la perpendiculaire issue de \(A\) coupe la parallèle passant par \(B\) en \(hB_e\), on peut avoir le troisième sommet possible \(C_{he}\) intersection des droites \((B \, hA_h)\) et \((A \, hB_e)\). Dans cette configuration, on notera que l’on a deux couples de hauteurs parallèles … mais pas sur les mêmes triangles, bien entendu.
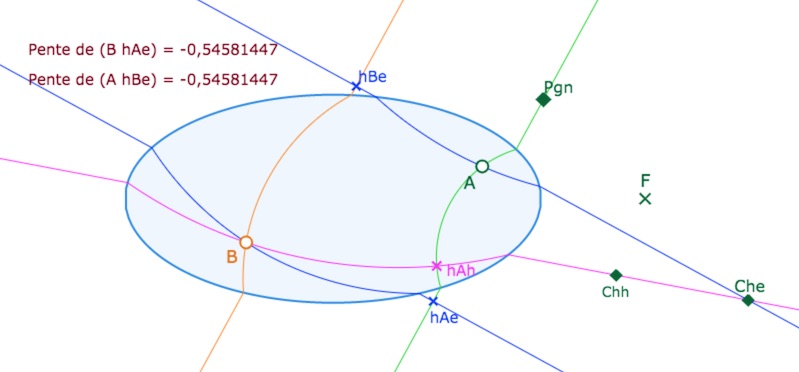
Le quadrilatère \(A \, hA_e \, B \, hB_e\) est un parallélogramme car le quadrilatère euclidien support est un parallélogramme avec deux angles droits, en \(hA_e\) et \(hB_e\), donc un rectangle :
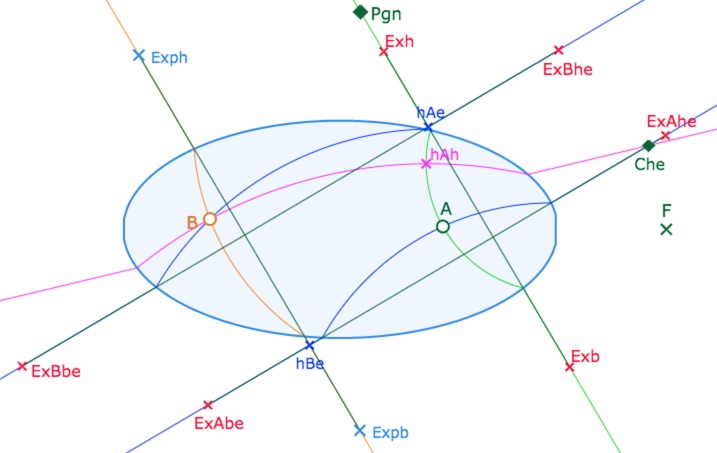
Cas où les quatre perpendiculaires existent
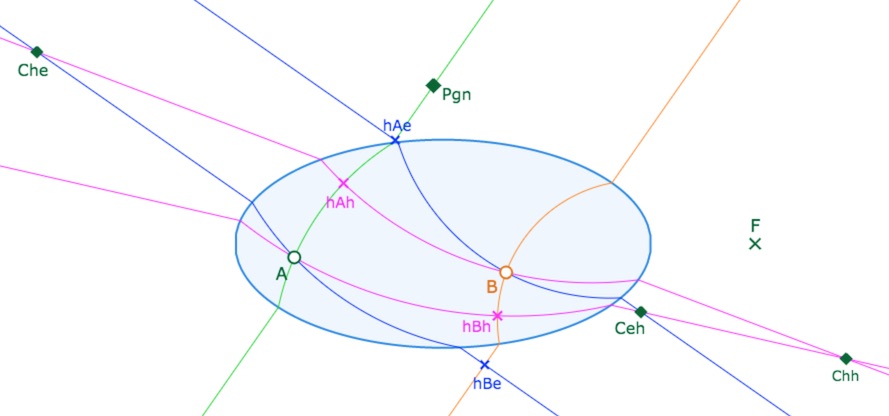
Dans ce cas il y a trois triangles solutions \(ABC_{hh}, ABC_{eh}, ABC_{he}\).
Une première réalisation
Comme indiqué dans la page qui traite de la construction des droites algébriques (la dernière section aborde celle des perpendiculaires), la macro-construction dédiée aux perpendiculaires construit toutes les perpendiculaires à une droite issue d’un point, et on sait qu’il peut y en avoir théoriquement jusqu’à 4, trois hilbertiennes et une euclidienne, et donc la mise en place des triangles \(ABC\) solution est essentiellement un jeu de « cacher/montrer » des droites.
C’est d’ailleurs en manipulant cette figure qu’est apparu cette possibilité, a priori surprenante, que les trois hauteurs hilbertiennes peuvent être réelles en même temps. En déplaçant la poignée \(Pgn\), le point \(B\), passant un instant par la droite \((Pgn \, A)\), peut donner, selon les configurations, cette illustration :
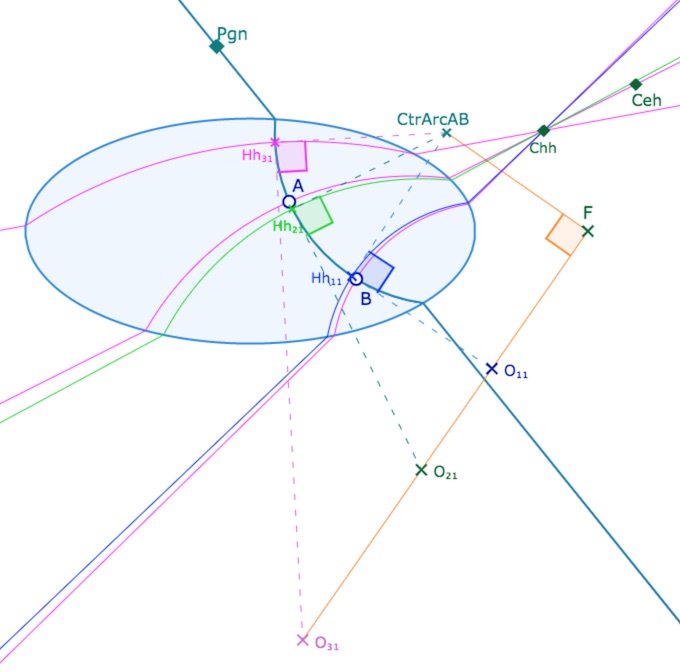
Premier cas rencontré de trois perpendiculaires hilbertiennes à une droite issues d’un même point.
Situation obtenue en manipulant une figure de travail.
Voir en ligne une figure d’animation (déjà présentée dans la page d’introduction à l’orthogonalité)
Pour se centrer sur la spécificité des hauteurs parallèles, on a fait le choix, dans la figure générique suivante, de volontairement cacher les hauteurs annexes comme celles-ci qui pourraient apparaître, exceptionnellement à l’occasion de certaines configurations.
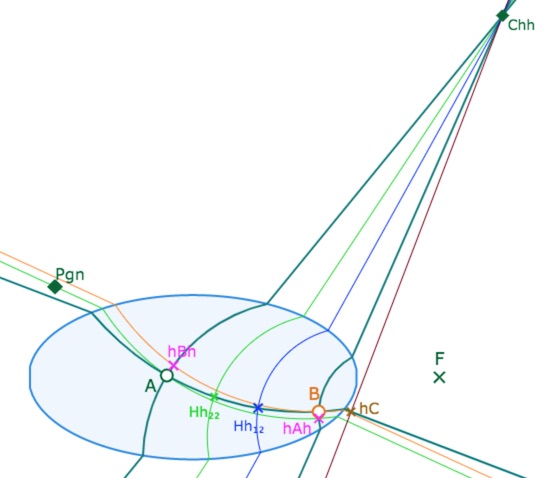
Exemple de situation qui n’apparaîtra pas dans la figure générique
La figure dynamique
En mode \(Libre\), agir sur les points \(Pgn, A\) ou \(B\).
Préférer ouvrir cette figure dans un nouvel onglet, peut-être plus facile à manipuler
Triangles orthocentriques dynamiques
ayant deux hauteurs parallèles
Cet article a surtout été rédigé pour cette section et la suivante, qui vont permettre d’aller plus loin que ce qui a été proposé dans les pages du menu Non Arg sur ce sujet.
Dans la figure générique précédente, on a construit les perpendiculaires (une ou deux) issues respectivement de \(A\) et \(B\) aux droites initiales, parallèles, ne contenant pas le point. On a ainsi \((A \; hA_h)\) ou \((A \; hA_e)\) comme hauteurs issues de \(A\), pour deux triangles différents. Mais la hauteur issue de \(A\) ainsi construite, par exemple dans \(ABC_{eh}\) peut ne pas être unique.
On construit donc, par la macro Perpendiculaire, les hauteurs issues de \(A\), ce qui rajoute une nouvelle hauteur, \((A \, hA_i)\). On cherche alors à rendre les trois hauteurs \((A \, hA_i), \; (B \, hB_h)\) et \((C \, hC_h)\) concourantes.
La figure dynamique – Avec une autre perpendiculaire issue de \(A\)
Si on déplace les points un peu trop vite, en particulier le point \(A\),
il peut être nécessaire de déactiver, puis réactiver le programme.
Lancer cette figure, proposée plus grande, dans un nouvel onglet
Variante avec une autre perpendiculaire issue de \(B\)
On peut faire la même chose avec le point \(B\), ce qui rajoute une autre hauteur, \((B \, hB_{e2})\). Voici une version simplifiée, la figure est un peu moins stable pour l’aspect dynamique.
Comme ci-dessus, si on déplace les points un peu trop vite, en particulier le point \(A\),
il peut être nécessaire de déactiver, puis réactiver le programme.
Si on n’obtient pas tout de suite la distance nulle entre les deux points, désactiver le programme et déplacer à la souris le point \(Pgn\), le programme n’étant efficace que pour deux points déjà très proches, car on a choisi une faible variation du point \(Pgn\).
Préférer ouvrir cette figure dans un nouvel onglet. Ne pas hésiter à tester alors des configurations très différentes, toujours en préparant la figure avec les deux points \(h_{ABe}\) et \(h_{BCe}\) très proches.
Exemple de triangle bi-orthocentrique
ayant deux hauteurs parallèles
On peut désormais tenter d’avoir deux orthocentres. On a donc trois contraintes : deux hauteurs parallèles – donnée initiale – un premier orthocentre (que l’on peut réaliser en maintenant une figure dynamique) et on essaie d’obtenir un second orthocentre. C’est assez facilement réalisable, mais a configuration obtenue est alors statique : on n’a aucune chance de maintenir les deux orthocentres par un déplacement d’un point, tout simplement car un déplacement à la main est de l’ordre d’une dizaine de pixels alors que tout se joue au delà du millionième de pixel.
Figure de départ
On a préparé une figure initiale en activant le programme d’une des figures précédentes, donc on part avec deux contraintes réalisée, la première stable, car initiale, celle des deux hauteurs parallèles, et un premier orthocentre, a priori lui non stable.
On a choisi de placer les deux programmes, celui sur \(Pgn\) et l’autre sur \(A\) dans une même boucle. La bonne surprise est, qu’en maintenant tout de même la même profondeur de l’algorithme sur le point \(Pgn\), le premier orthocentre reste stable. On a largement augmenté la profondeur du second programme pour que le nombre d’étapes pour arriver à l’orthocentre ne soit pas aussi grand que dans les pages de découverte du menu Non Arg, ou parfois il fallait plus de 30 étapes pour arriver seulement à deux contraintes (soit deux orthocentres soit un orthocentre et deux hauteurs parallèles).
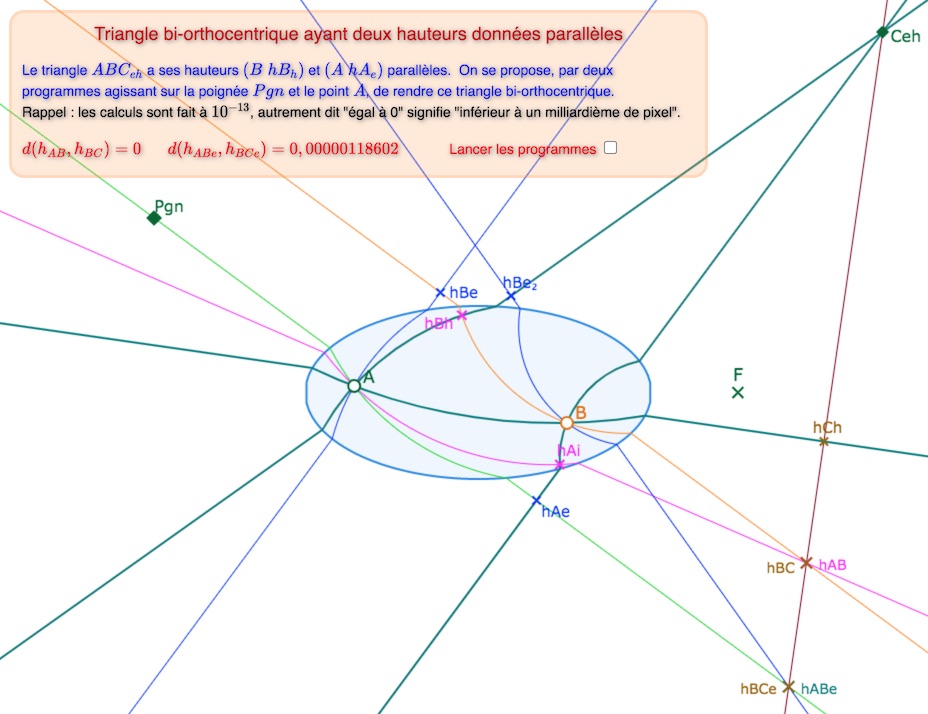
Les étapes
La seule chose à faire est de cocher et décocher le programme, huit fois. Avant de commencer on peut tenter de modifier légèrement le point \(B\) et ajuster au mieux avec le point \(Pgn\). Il faudra probablement une ou deux étapes supplémentaires.
Les 7 premières étapes avant le résultat final.
Attention : le temps de réalisation de chaque étape est de plusieurs secondes.
Lancer la figure pour activer ces 7 étapes … et la huitième dans un nouvel onglet.
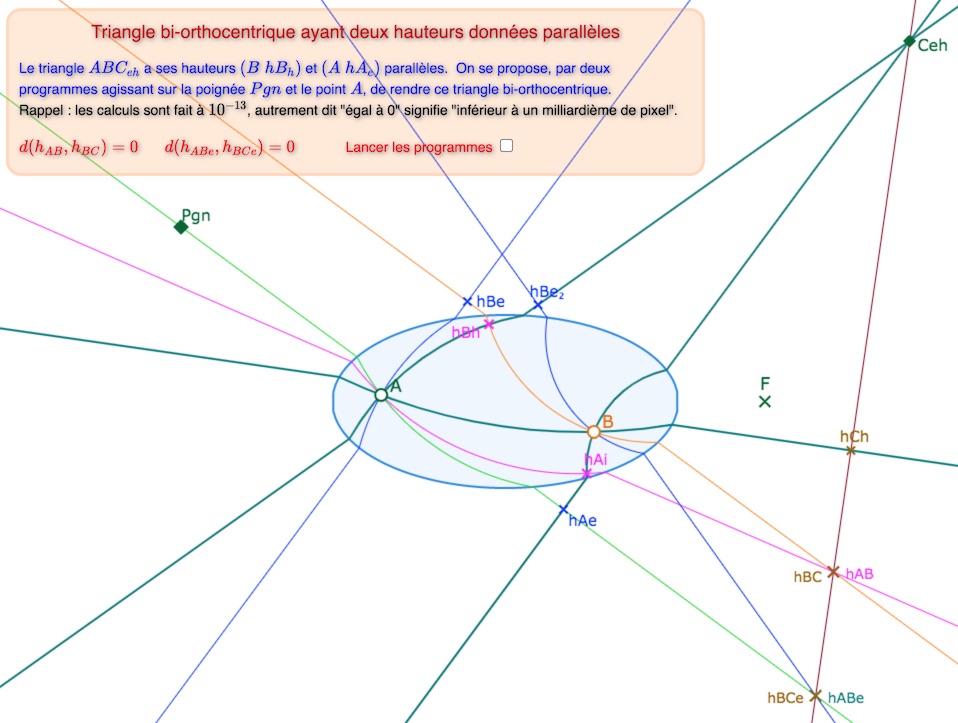
La huitième et dernière étape : obtention d’un triangle bi-orthocentrique ayant deux hauteurs parallèles.
Préférer ouvrir la figure finale aux trois contraintes réalisées dans un nouvel onglet.
Néanmoins aucune chance de conserver la bi-orthocentricité en déplaçant un point, mais on peut tenter de relancer plusieurs étapes dans une nouvelle configuration.
Bilan de l’article
Dans les pages du menu Non Arg, en particulier, Triangles bi-orthocentriques ou encore Triangles orthocentriques avec deux hauteurs parallèles, les deux contraintes aboutissaient à des figures statiques.
Ici, on peut conserver la manipulation d’une figure avec deux contraintes. C’est seulement à la troisième contrainte que l’on passe à des configurations statiques.
Dans un prochain article, on cherchera la bi-orthocentricité dynamique, un premier orthocentre étant donné initialement.







