Dans cet article, on propose une première famille de macros pour réaliser soi-même des figures dans le disque de Poincaré. Un autre article sera consacré aux pavages avec des macros spécifiques.
Quelques unes de ces macros ont été optimisées pour cet article, en janvier 2024, il est donc préférable d’utiliser les macros de cette page plutôt que des macros de figures antérieures qui peuvent être un peu moins optimisées. J’ai tardé à écrire cette page car, utilisant très souvent le disque de Poincaré (menu Bachmann, articles Bolyai et suivants), je modifie en permanence mes propres macros. J’ai profité des « bonnes résolutions de janvier » pour faire un tri un peu structuré.
Bien entendu, il faut avoir déjà pratiqué les macro de DGPad. Pour cela on peut revoir cette page de présentation des macros du logiciel, ou encore regarder quelques unes des pages précédentes sur les macros (en prenant les plus simples, éviter la géométrie non arguésienne par exemple)
La réalisation technique de quelques macros est détaillée en fin d’article. C’est à considérer comme une petite « ouverture du capot » qui n’intéressera que quelques lecteurs. C’est peut-être aussi une simple mise en mémoire personnelle.
Les macros de base proposées
Cette première série de macros comprend cinq dossiers très classiques sur lesquels on va donner quelques précisions. Tout d’abord, on ne voit que les quatre premières lignes dans les macros personnelles, donc quand il y a plus de quatre macros, il faut faire dérouler les macros.
Ensuite, d’une manière générale, toutes les macros ont comme premier objet initial le cercle horizon.
Toutes … sauf une ! la macro 3 du dossier Points, celle de symétrie orthogonale par rapport à une droite hyperbolique qui n’a pas besoin du cercle horizon. Précisons un peu.
Le dossier 1.Points
Sym ortho Arc 1 pt : le premier objet est une droite hyperbolique, soit un arc de cercle euclidien, et le second objet est le point.
Sym ortho Cercle 1 pt : elle aussi demande seulement un cercle et un point. Mais elle ne sera en générale utilisée – pour des situations bien spécifiques – qu’avec le cercle horizon. C’est pour cela qu’elle n’est pas comptabilisée comme « différente ». Dans cet article, on s’en servira deux fois dans la section « pavage non constructible ».
Le fait qu’il y ait ces deux macros 3 et 5 du dossier Points pour un même résultat, vient de la différence des objets constitutifs des arcs de cercle et des cercles.
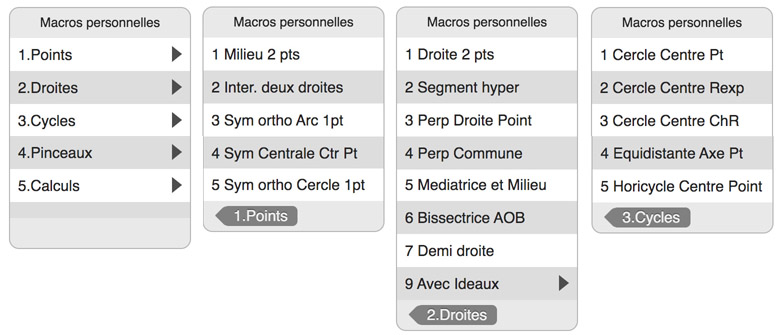
Intersection de deux droites : comme on l’a largement détaillé sur la page Continuité et déterminisme de présentation de DGPad, dans le contexte des droites hyperboliques il faut utiliser une macro pour que le point d’intersection de deux droites ou segments hyperboliques soit indépendante de l’orientation euclidienne des objets utilisés.
La distance entre deux points est placée dans le dossier 5.
Le dossier 2.Droites
Rien de particulier à préciser. On peut néanmoins signaler que si une droite devait être définie par deux points idéaux, on peut utiliser la macro Segment, cela utilisera moins d’objets intermédiaires. Le dossier 9 Avec Idéaux est présenté plus loin.
Le dossier 3.Cycles
Il y a trois macros de cercles, une première, usuelle, par centre et point, et une seconde par centre et rayon donné sous forme d’une expression, et une troisième par centre et \(ch(r)\) le cosinus hyperbolique du rayon car c’est souvent par son \(ch\) qu’une longueur est donnée, en particulier en trigonométrie hyperbolique. Cette macro permet de construire, par exemple, un triangle d’angles donnés quelconques. Ci-dessous on a utilisé les deux macros de cercle avec une expression, juste pour tester leur validité.
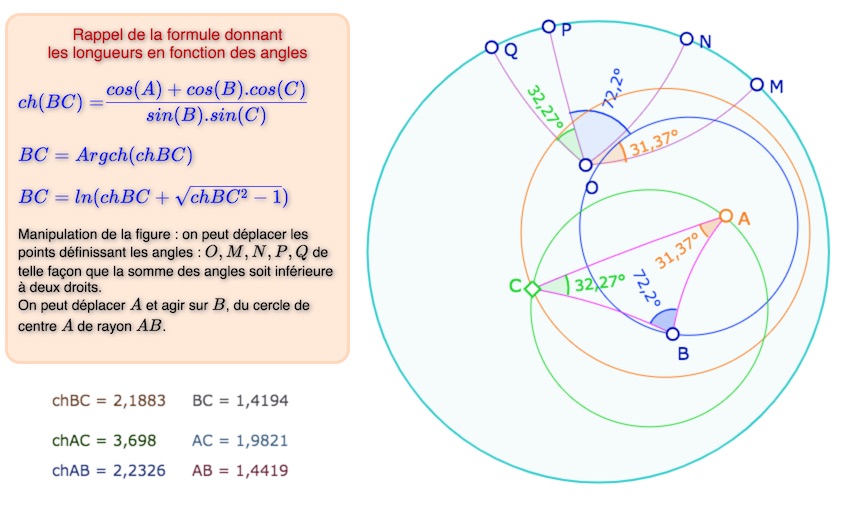
On peut commencer par reproduire cette simple construction avec la figure proposée en fin de cette section. On peut simplement préférer lancer cette figure dans un nouvel onglet.
Dans ce dossier Cycles, il y a aussi l’équidistante, et simplement l’horicycle par centre (qui est un point idéal) et un point.
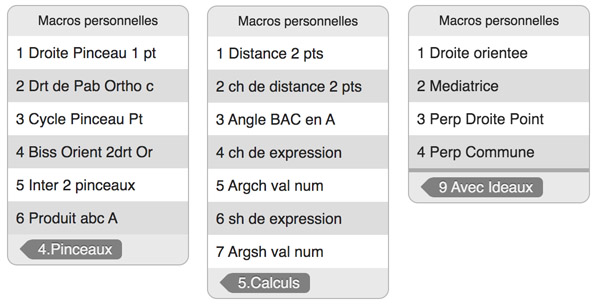
Le dossier 4.Pinceaux
Pour ces macros, il faut donner d’abord le cercle horizon comme d’habitude puis, selon les macros, deux ou plusieurs droites hyperboliques. Par exemple pour la macro des hauteurs : 2 Dtr de Pab Ortho, on montre le cercle horizon, deux droites définissant un pinceau et la droite dont on veut la perpendiculaire issue du pinceau. L’intersection de deux pinceaux attend 4 droites après le cercle horizon.
Cycle Pinceau Pt construit le cycle (cercle ou équidistante selon que le pinceau soit « à centre » ou « à axe ») image d’un point par un pinceau. La macro est « minimaliste » dans la mesure où l’on n’a pas ajouté l’horicycle qui nécessiterait un traitement un peu plus lourd alors que, sauf si elle est provoquée – par exemple par une aimantation – la situation ne se rencontre jamais en manipulation directe.
Voici un exemple classique d’utilisation : le cycle inscrit d’un trilatère
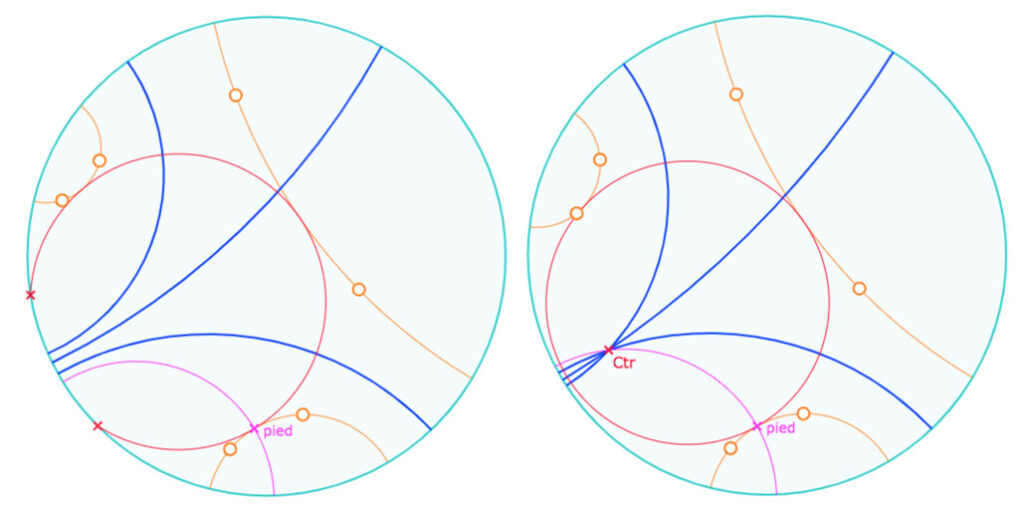
Étant donné un trilatère – les trois droites en orange – on construit ses bissectrices, par la macro présentée après celle-ci, ce sont les droites bleues plus épaisses. On cherche à avoir un point du cycle inscrit, indépendamment du type de cycle. Pour cela on prend la perpendiculaire à une droite du trilatère issue du pinceau de deux des bissectrices. Cela donne la droite rose, avec le point « pied » (par la macro Intersection de deux droites). La macro Cycle Pinceau Pt appliquée au cercle horizon, deux des trois bissectrices et le point « pied » donne l’équidistante à gauche avec ses deux points idéaux, et en même temps le cercle à droite avec l’intersection des droites du pinceau quand il devient « à centre ». On n’a pas ajouté dans la macro l’axe des bissectrices quand le pinceau est « à axe » car il est souvent déjà tracé. Mais si on devait le faire, il suffit de construire le segment (plutôt que la droite) passant par les deux points idéaux marqués d’une petite croix. Et bien entendu, on illustre que le cycle construit est tangent aux deux autres droites du trilatère.
Biss Orient 2 drt Or construit un axe de symétrie de deux droites, soit sa bissectrice quand les deux droites ne sont pas sécantes ou une des deux bissectrices si elles sont sécantes. On sait qu’il y a là une difficulté compte tenu des limites théoriques qui existent entre la continuité et le déterminisme. C’est pour cela que cette macro utilise – si on l’a anticipé, et c’est préférable – des droites orientées (voir le dossier 9 Avec Idéaux) ce qui permet de réaliser une bissectrice de deux droites qui reste le plus « longtemps possible » dans la continuité d’une des deux bissectrices quand ces deux droites deviennent sécantes. Mais on sait que, quelque soit le traitement prévu, cela ne peut maintenir complètement continuité et déterminisme. Cette macro a été mise au point pour plus de continuité dans les « quadrisectrices » (bissectrices de bissectrices) dans la construction de Malfatti de trilatères dans le disque de Poincaré (voir par exemple la galerie au sujet de « la construction »).
Produit abc A, est une macro plus dans l’esprit « Bachmann » car elle renvoie le produit de trois droites. Les objets initiaux sont, le cercle horizon, les trois droites dans l’ordre où l’on veut le produit et un point de la première droite choisie.
Le dossier 5.Calculs
Ce sont d’abord trois macros de base, la distance de 2 points, le cosinus hyperbolique de la distance de deux points ch de distance 2 pts et la mesure d’un angle, en ne donnant, après le cercle horizon, que 3 points, les centres des arcs de cercles étant recalculés dans la macro. Plusieurs autres macros sur les angles peuvent être découvertes dans les figures du site, elles n’ont pas été reprises, étant souvent spécifiques d’une situation.
Les quatre dernières macros complètent le « clavier mathématique » qui s’ouvre quand on active l’outil expression avec les lignes trigonométriques hyperboliques les plus utilisées.
Le dossier 9.Avec Points idéaux
Ces macros sont les mêmes que celles du dossier 2 sur les droites, où l’on fait apparaître les points idéaux. Toutefois, la première renvoie une droite orientée : soient deux points \(A\) et \(B\) la macro renvoie la droites avec ses points idéaux \(IdAor\) et \(IdBor\) qui restent, respectivement du côté de \(A\) et \(B\) quelque soit l’orientation de l’arc de cercle représentant la droite, ce qui n’est pas le cas des autres macros de droites du dossier 2.
La médiatrice de 2 points avec ses points idéaux permet de construire tout de suite, simplement par l’item euclidien « Cercle par 3 points » de la palette d’outils de DGPad, les deux horicycles passant par ces deux points. On notera que l’éventuelle inversion des points idéaux pendant la manipulation n’est pas un problème dans ce cas.
Lancer la figure de base avec toutes ces macros dans un nouvel onglet.
Dans les deux sections suivantes on propose différentes constructions, d’abord, dans la première, sur des figures de bases, et dans la seconde, on propose un (début) de pavage non constructible à la règle et au compas.
Proposition de quelques figures à réaliser
pour manipuler ces macros
Premier contact – Le cycle circonscrit d’un triangle
On peut commencer par des figures de triangles : le cycle circonscrit est l’occasion d’utiliser une macro de pinceau : Cycle par pinceau et point : deux médiatrices et un sommet du triangle, cela crée donc à la fois le cercle, comme à gauche, et l’équidistante, comme à droite.
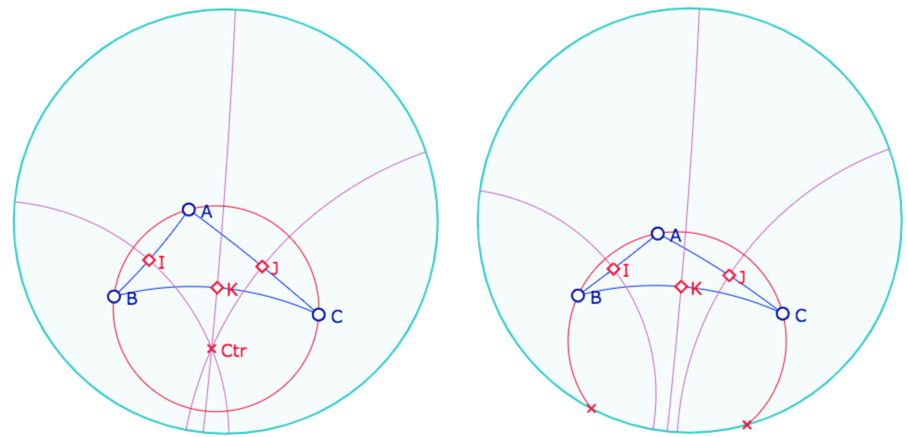
Comment forcer le cycle circonscrit à devenir un horicycle ?
Cette figure élémentaire est l’occasion de montrer comment incorporer le cas des médiatrices « sans support » dans une figure – plus généralement « le cas sans support » dans n’importe quelle figure. Pour cela, il faut reprendre cette figure avec une des médiatrices – celle de \(A\) et \(B\) – avec ses points idéaux.
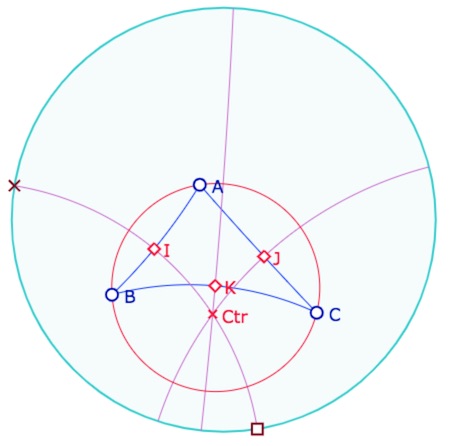
Pour tester rapidement la manipulation suivante on peut lancer la figure en cet état dans un nouvel onglet. Avec la palette de construction (donc flèche gauche du tableau de bord activée) utiliser l’outil Cercle par trois points en l’appliquant au point carré et construire le cercle circonscrit passant par ce point carré, le point \(B\) (illustration de gauche en cours de manipulation) et au point \(A\) (illustration de droite).
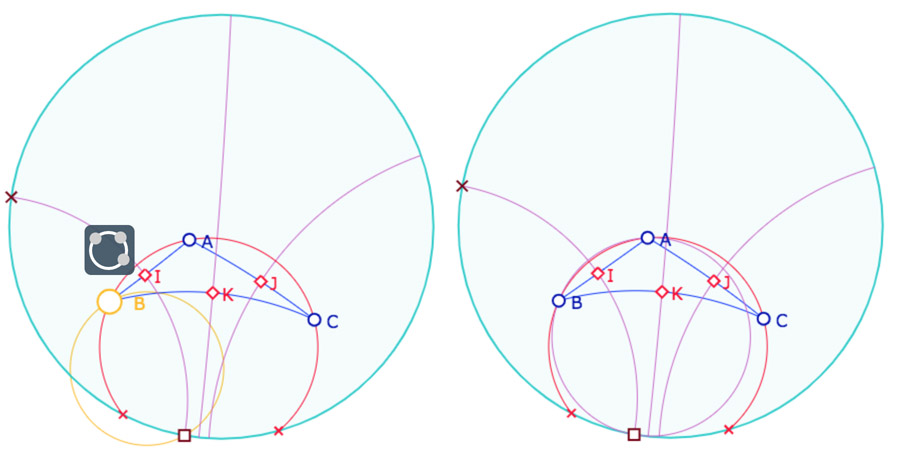
Le futur horicycle est ainsi tracé. Reste à y « coller » le point \(C\). Cela se fait avec l’outil Aimantation de la palette de comportement comme ceci :
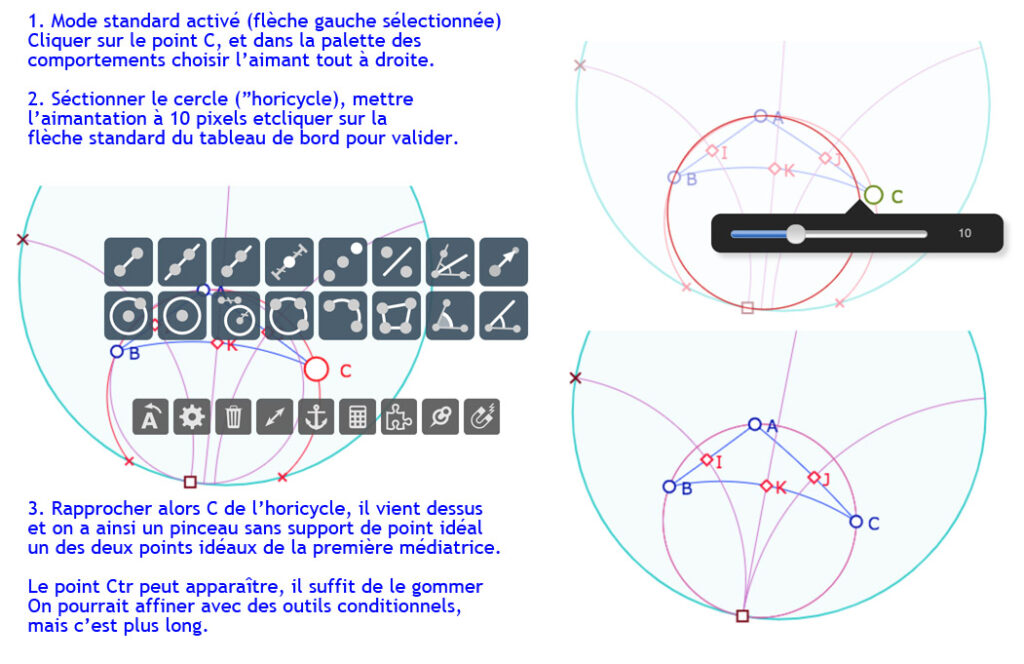
Préférer lancer la figure finale (avec les améliorations conditionnelles) dans un nouvel onglet.
Dans la suite on ne détaillera pas les constructions.
Le cercle inscrit et les cycles exinscrits
Lancer la figure de base avec toutes ses macros dans un nouvel onglet.
On peut continuer sur les triangles comme cette figure déjà proposée dans le menu DP. On utilise la même démarche que ci-dessus avec la macro Cycle par pinceau et point.
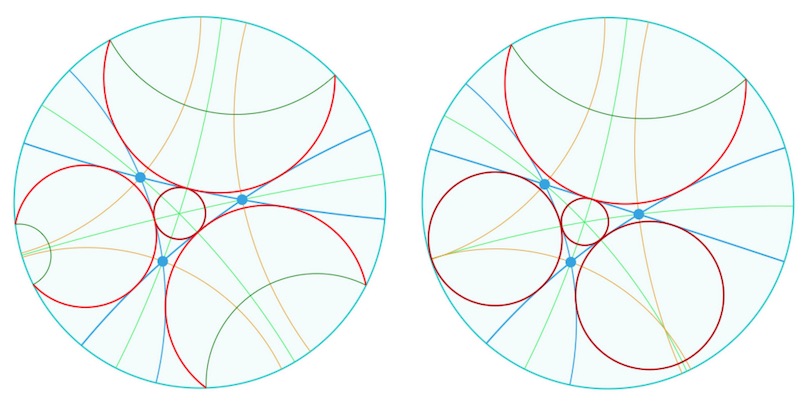
à gauche trois équidistantes circonscrites, à droite, un cercle, une équidistante et un horicycle.
Jouer avec les macros du dossier 5
On peut s’amuser aussi à illustrer les formules de géométrie hyperbolique comme les ont montrées Bolyaï et Lobatchevsky. Voici un rappel de ces formules déjà illustrées à la fin de cet article sur le manuscrit de Bolyaï :
Lancer la figure de base avec toutes ses macros dans un nouvel onglet.
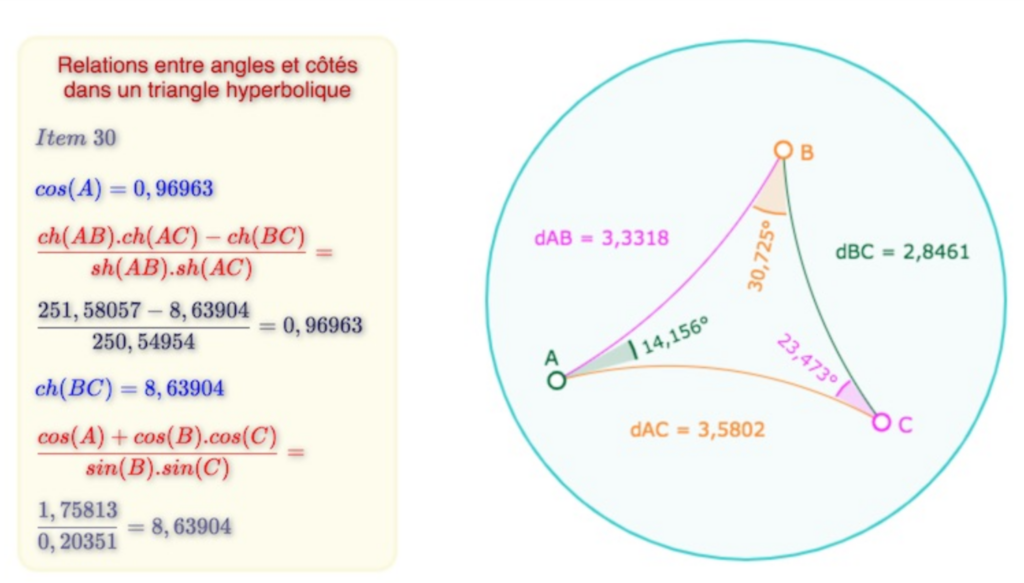
ou encore dans le triangle rectangle
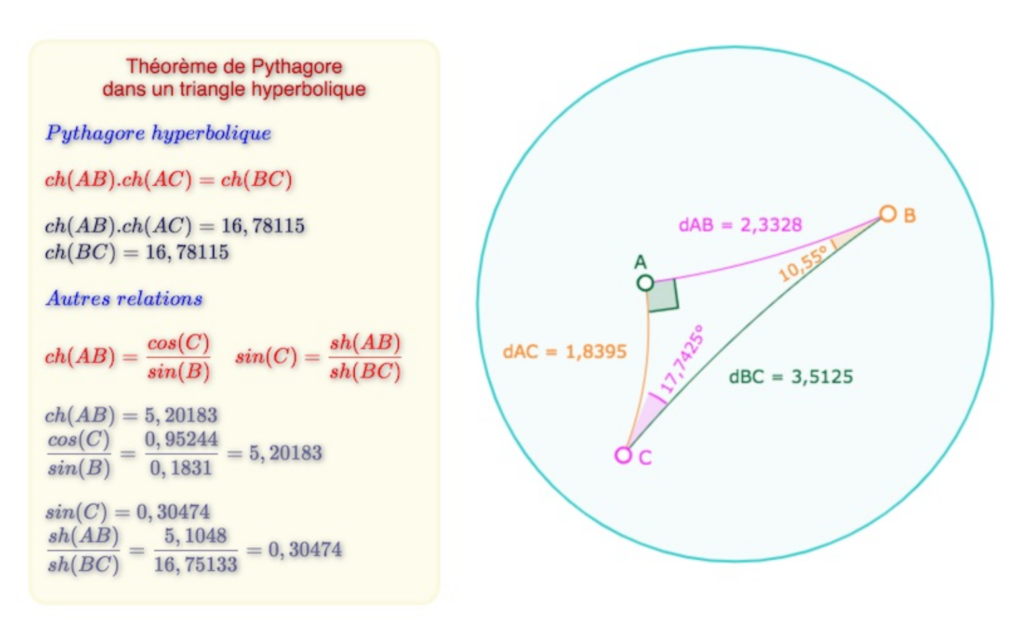
Le triangle podaire d’un trilatère
On propose de poursuivre avec les trilatères, mais ces figures peuvent se faire aussi sur des triangles. Le pinceau des hauteurs d’un trilatère est aussi le pinceau des bissectrices du triangle des pieds des hauteurs. Il y a un cycle inscrit ou exinscrit.
Lancer la figure de base avec toutes ses macros dans un nouvel onglet.
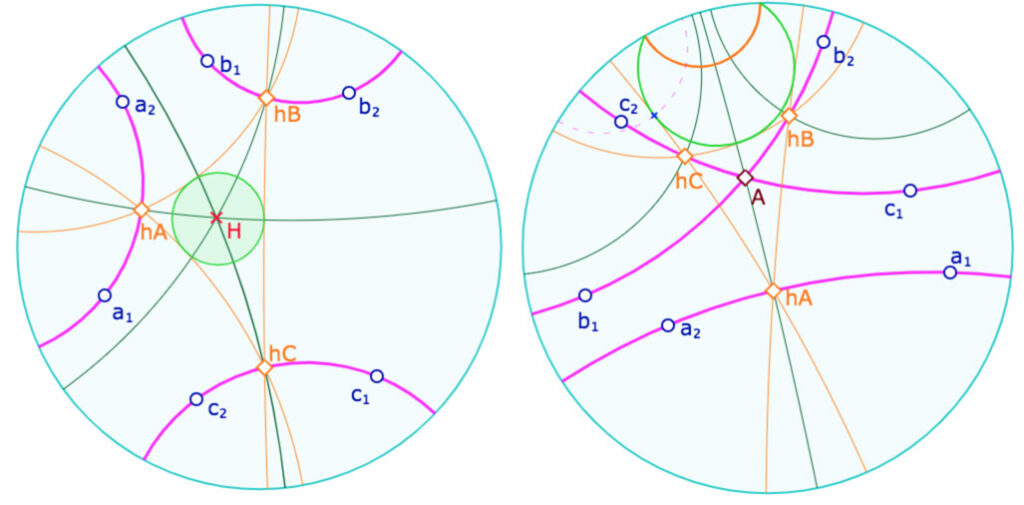
à gauche le cercle inscrit classique (des triangles), à droite une équidistante exinscrite au triangle podaire
Le point de Gergonne d’un trilatère
On commence par construire le cycle inscrit (à gauche le cercle, à droite une équidistante) puis les points de contact (à gauche \(h_A, h_B, h_C\), à droite \(e_A, e_B, e_C\), ce sont des points différents), puis les droites des pinceaux de deux droites passant par le point de contact de la troisième droite.
Lancer la figure de base avec toutes ses macros dans un nouvel onglet.
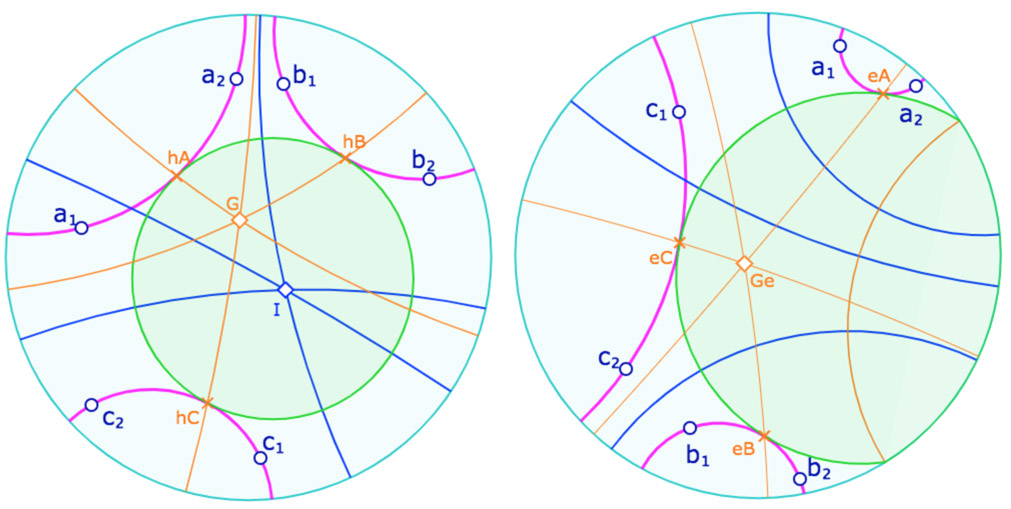
Le remplissage de droite est juste esthétique, il n’a pas de sens mathématique. Dans un prochain article, on proposera plusieurs dossiers de remplissages pour faire cela automatiquement.
Les points bissecteurs d’un trilatère
C’est plus technique, mais cela peut être intéressant.
Lancer la figure de base avec toutes ses macros dans un nouvel onglet.
On construit les points bissecteurs d’un trilatère, les points \(I, J, K\) ci-dessous, en suivant les détails de cette reprise d’une page sur l’axiomatique de Bachmann.
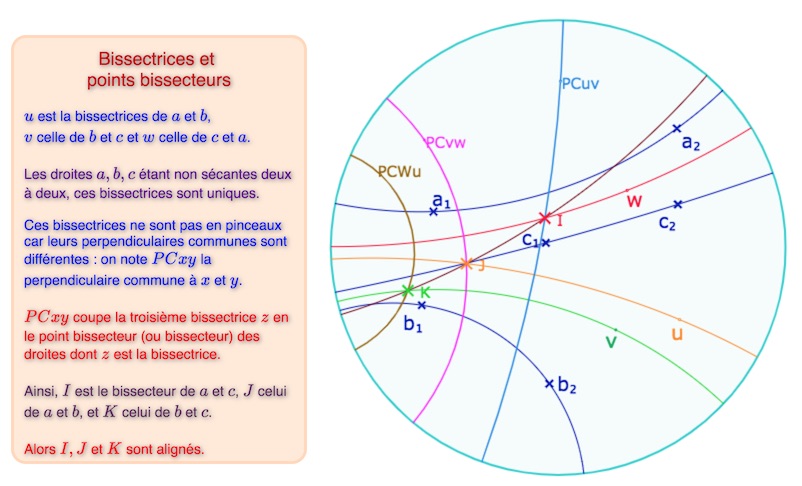
On peut aussi choisir d’ouvrir cette figure AVEC les macros de cette page pour faire la manipulation suivante :
Simplement prendre un point sur l’une des droites de base du trilatère, puis, avec la macro de point Symétrie centrale, faire le symétrique de ce point par rapport aux deux points bissecteurs concernés par cette droite et vérifier (de visu), en déplaçant le point, que l’image appartient à l’autre droite dont le point est bissecteur avec la droite choisie.
Réaliser un pavage non constructible
On rappelle qu’en notant \(r_{nk}\) le rayon du cercle de pavage de \(P(n,k)\) et \(ch_{nk}=ch(r_{nk})\) on a \(ch_{nk}=\displaystyle cotan \left( \frac{\pi}{n} \right) \; cotan \left( \frac{\pi}{k} \right)\). On a déjà réalisé de nombreux pavages constructibles dans ce précédent article. Mais ici, avec le compas de rayon \(ch(r)\), on se propose de construire la génération 1 du « plus petit » pavage réalisable, à savoir \(P(7,3)\), puisque \(\displaystyle \frac{1}{7} + \frac{1}{3} = \frac{10}{21} < \frac{1}{2}\), et c’est le plus proche de \(\displaystyle \frac{1}{2}\) de tous les pavages possibles.
On a donc \(ch_{73}=\displaystyle cotan \left( \frac{\pi}{7} \right) \; cotan \left( \frac{\pi}{3} \right)\).
Lancer une nouvelle figure avec les macros précédentes et quelques autres (pour la surprise finale !) dans un nouvel onglet.
Le cercle de pavage
On continue de travailler en degrés, donc on entre cette expression, puis on construit le cercle de pavage par la macro Cercle Centre ChR depuis un point \(O\).
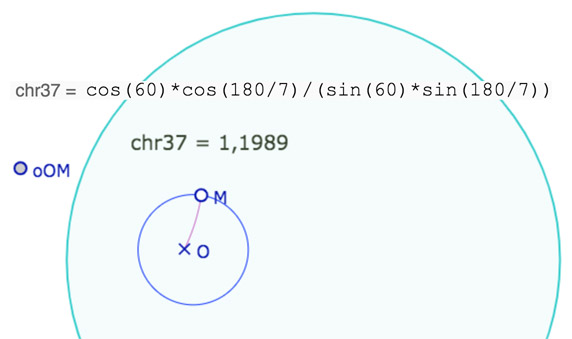
On prend ensuite un point \(M\) sur le cercle, puis on construit le segment \([OM]\), et, avec la gomme activée, on montre le centre du cercle qui est a priori caché. Il n’est pas nommé \(oOM\) par défaut, on l’a renommé avec la palette d’aspect des objets (icone roue du tableau de bord).
La rotation de centre \(\mathbf{O}\) d’angle \(\mathbf{\displaystyle \frac{2\pi}{7}}\).
C’est la seule partie qui nécessite de connaitre un peu plus le logiciel. Tout d’abord pour éviter les problèmes d’orientation on va obtenir la première image de la rotation par la symétrie orthogonale de \(M\) par rapport à la bissectrice de l’angle, donc par une rotation d’angle moitié \(\displaystyle \frac{2\pi}{14}\), soit \(\displaystyle \frac{\pi}{7}\). Cela se construit sur la base que le modèle est conforme, donc avec les tangentes euclidiennes aux droites hyperbolique. En pratique on fait comme ceci :
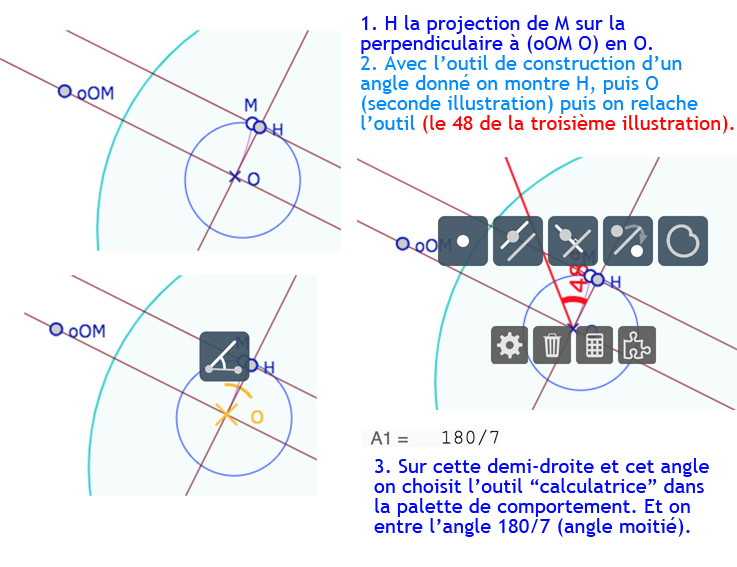
On a donc la tangente euclidienne à \([OM]\) et l’angle voulu par rapport à cette tangente pour construire la droite hyperbolique tangente à cette demi-droite passant par \(O\).
Passant par \(O\) : le centre est sur la médiatrice de \(O\) et de son inverse \(invO\) par rapport au cercle horizon : c’est une occasion d’utiliser la 5° macro du dossier Point : Sym Ortho Cercle 1pt. Le centre est aussi sur la perpendiculaire en \(O\) à la demi-droite tangente (demi-droite verte ci-dessous). On a le centre euclidien de la droite hyperbolique cherchée : on construit le cercle de centre ce point passant par \(O\). C’est la bissectrice de l’angle au centre de l’heptagone entre \(M\) et le premier point A de l’heptagone. Et donc, à nouveau, l’inverse « Sym Ortho Cercle 1pt » par rapport à cette droite (sous sa forme préliminaire du cercle marron) donne le point \(A\). On construit, avec la macro Droite 2 pts, la droite \((OA)\) : on a ainsi un second axe de symétrie de l’heptagone.
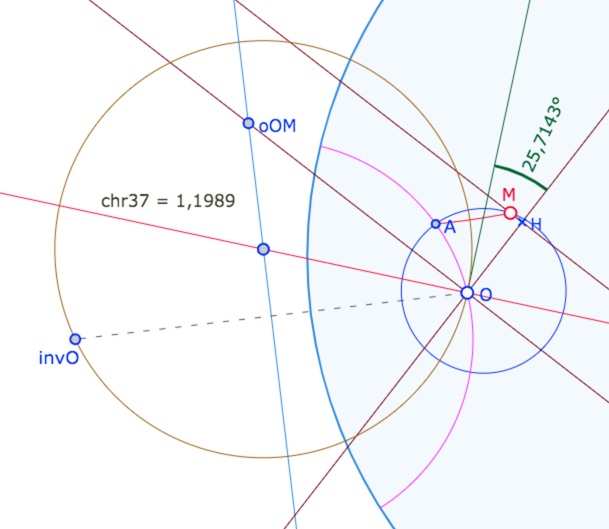
Le premier heptagone et vérifications numériques
Les deux axes de symétrie \((OM)\) et \((OA)\) suffisent pour construire l’heptagone régulier, on arrive alors très vite à cette première étape (à gauche).
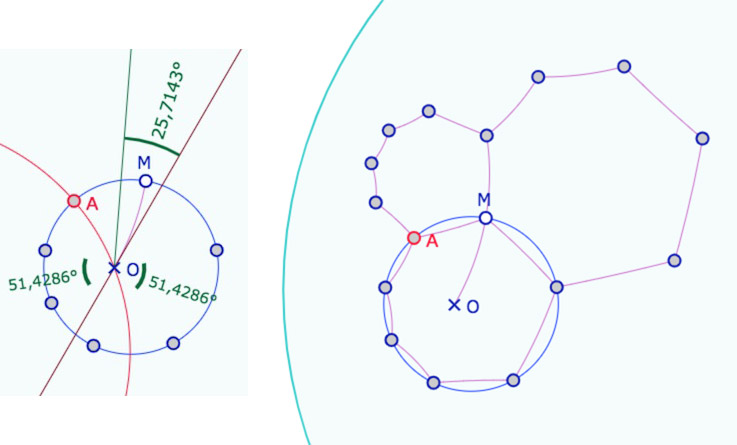
On peut choisir aussi de lancer une figure préconstruite avec l’heptagone central.
Puis on termine rapidement la génération 1 de ce pavage
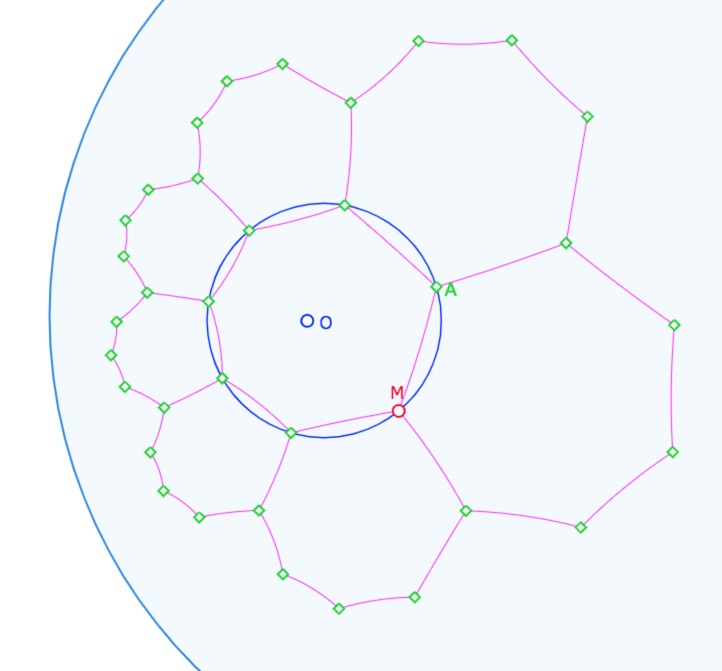
Petit bonus
Les deux figures précédentes au lancement contiennent des macros supplémentaires de remplissage d’heptagones. On montre le cercle horizon et les 7 points de l’heptagone. Ces macros ajoutent des « listes de segments » et donc pas vraiment d’objets (même les centres des segments sont recalculés) : chaque remplissage est « un objet » de la construction. C’est une des (nombreuses) subtilités du logiciel.

On peut donc jouer avec pour faire des choses comme cela :
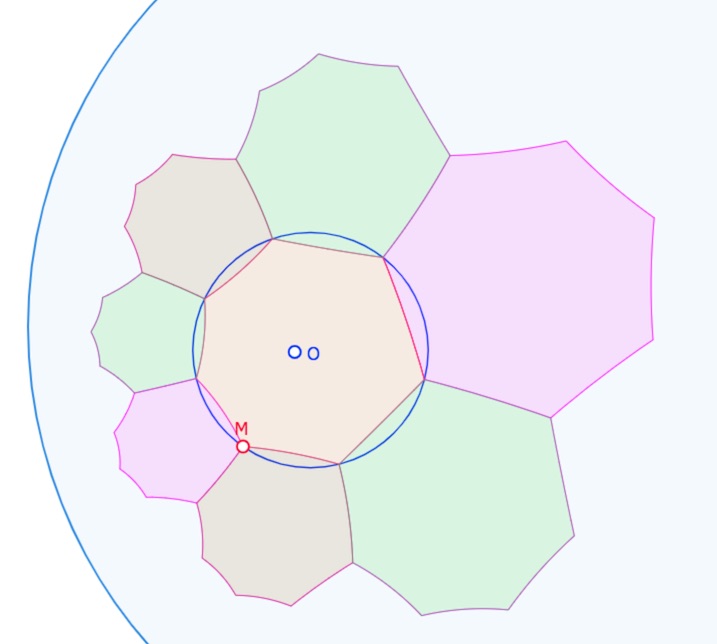
On peut lancer cette figure finale dans un nouvel onglet … mais c’est aussi très sympa de la faire soi-même …
Compléments : les générations 2 et 3
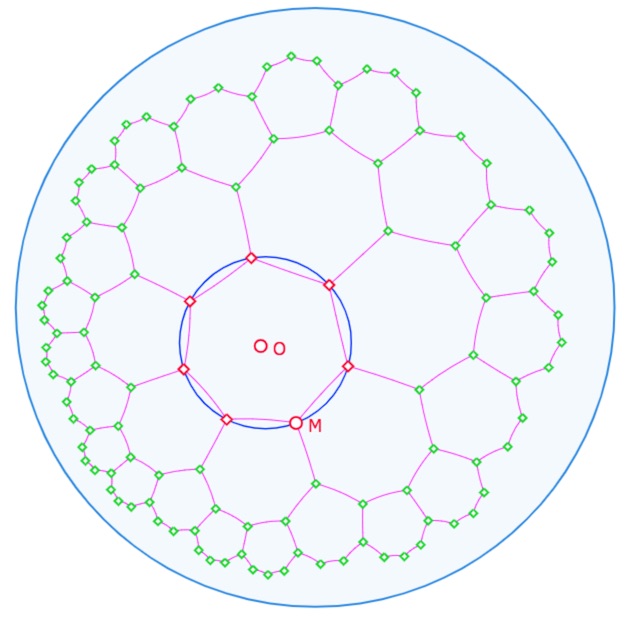
Lancer cette figure dans un nouvel onglet (\(M\) est animé, déplacer \(O\) pendant l’animation)
Et la génération 3
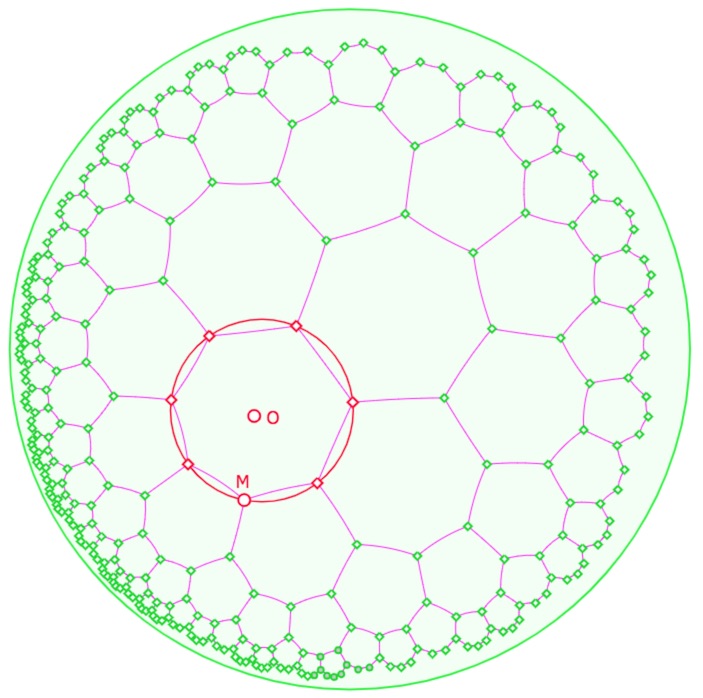
Lancer cette figure dans un nouvel onglet (\(M\) est animé, déplacer \(O\) pendant l’animation).
Le lien avec la « quartique de Klein »
Si vous ouvrez des ouvrages de géométrie hyperbolique ou des articles sur les pavages hyperboliques, ce premier pavage \(P(7,3)\) – c’est-à-dire d’heptagones d’angles de 120° – est plutôt présenté avec des triangles rectangles, en prenant la bissectrice de \(MOA\) des figures précédentes. On parle alors du pavage \(P(2, 3, 7)\), ce qui signifie alors qu’il est construit à partir de triangles d’angles respectivement \(\displaystyle \frac{\pi}{2}, \frac{\pi}{3},\frac{\pi}{7} \). Il est alors souvent présenté sous cette forme :
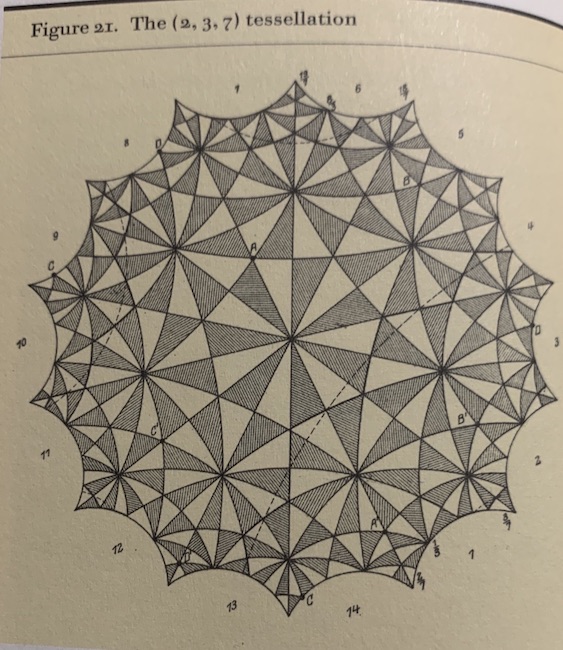
Pour passer du pavage précédent à celui-ci, il suffit de prendre le milieu des points \(A\) et \(M\), le reste se fait par des symétriques par rapport à un segment ou une droite hyperbolique. Mais on voit bien qu’il y a autre chose dans cette construction. Il s’agit d’une représentation hyperbolique du groupe simple d’ordre 168 de la quartique de Klein.
C’est assez technique et nécessiterait un article dédié. En attendant, on peut consulter cette vidéo de Jos Leys ou celle-ci du même auteur (336 triangles et 24 heptagones) ou, plus liée directement aux heptagones, cette vidéo de Tim Hutton (2 min) mais aussi les conférences de Daniel Perrin sur le sujet (sur la quartique de Klein, les deux conférences de 2008 et les 7 figures associées – faites alors en Cabri-géométre à l’époque). voici une version dynamique où on peut déplacer le centre \(a\) du premier heptagone et \(M\) sur le cercle de pavage, avec les notations de Daniel Perrin dans sa « figure 7 »..
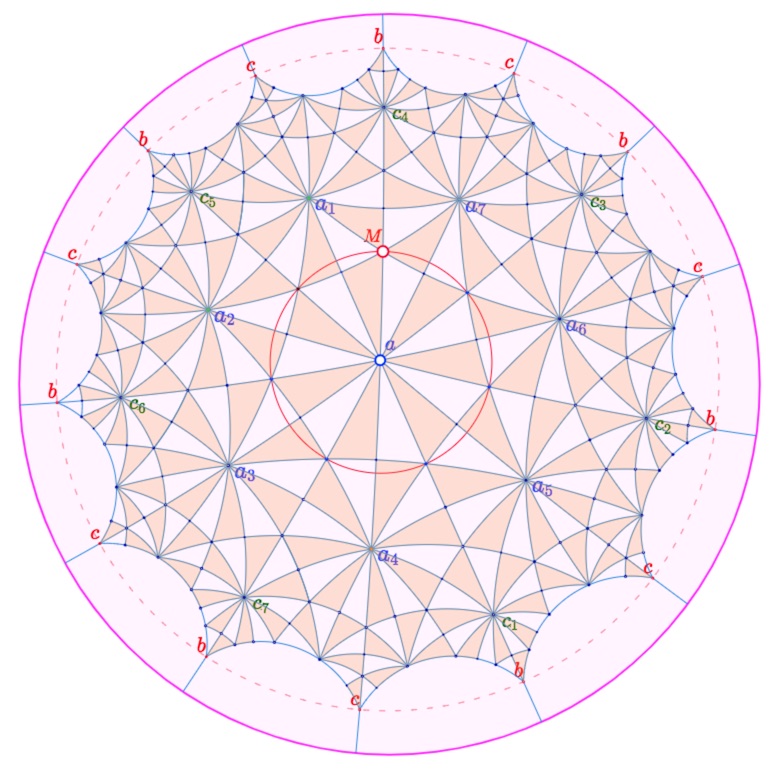
Lancer cette figure dans un nouvel onglet.
Les détails de construction de quelques macros algébriques
Même si parfois les réalisations d’objets peuvent être présentées, dans les menus du site, sous leur forme géométrique, les transformations en macro-constructions sont souvent bien plus algébriques. C’est en particulier le cas pour les macros utilisées en grand nombre dans les pavages, comme les segments, les droites, les symétriques, ou encore l’intersection de deux droites.
Segment
Pour donner un ordre d’idée, voici la macro qui construit un segment hyperbolique dans DP

Cette macro ne construit que deux objets intermédiaires : le centre du cercle euclidien support du segment, c’est le point \(oAB\), et le milieu du segment hyperbolique, le point \(PrMil\).
On notera l’écriture « Seg »\(+A+B\) qui permet de donner en suffixe du nom d’un segment les points utilisés. Cela peut être intéressant didactiquement pour des figures élémentaires, c’est sans intérêt pour des figures de pavage par exemple, cela alourdi la figure d’avoir des noms de segment SegP112P114 par exemple, c’est pour cela que l’on proposera, au prochain article, dans des listes de macros par thème, plusieurs variantes – d’affichage – de cette macro (et d’autres) selon les usages que l’on veut en faire.
Droite avec ses points idéaux

On observe la même démarche, il faut 3 points pour déterminer une droite hyperbolique : le centre du cercle, les deux points idéaux. On en a ajouté un quatrième, le fameux point milieu d’entre \(A\) et \(B\). Cela a été choisi pour qu’aucun des deux points de définition de la droite ne soit privilégié dans la construction. Mais c’est discutable bien entendu. Cette macro renvoie les points idéaux. Cela peut être utile, souvent cela alourdi inutilement la figure, là encore plusieurs variantes d’affichage sont proposées. Par exemple, dans cette macro les points idéaux sont « non orientés » c’est pour cela qu’il sont suffixés des deux points constitutifs de la droite. Une autre macro dite « droite orientée » où les points idéaux sont propres au point le plus proche est aussi disponible. Cela ne sert pas souvent, essentiellement pour une plus grande continuité sur les bissectrices.
Distance de deux points par les nombres complexes
DGPad a cet avantage de pouvoir utiliser naturellement les points comme affixes de nombres complexe : on peut les multiplier, prendre leurs conjugués ou leurs modules. Dans ce contexte, plutôt que d’utiliser la formule classique de la distance de deux points qui fait intervenir les points idéaux de la droite (on le fera quand même dans la macro « milieu et médiatrice »), on choisit, pour la macro générale de la distance entre deux points d’utiliser la formule ne faisant intervenir que ces deux points, sous cette forme :
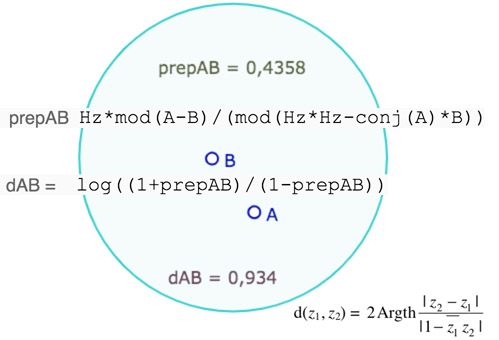
La formule est donnée dans le cadre d’un disque de Poincaré de rayon 1 (le « cercle fondamental »), il faut l’adapter au rayon du cercle utilisé. Dans DGPad, \(Hz\) est à la fois le nom du cercle, et en même temps une variable qui représente son rayon. On a donc la distance de deux points avec un objet intermédiaire qui est l’expression du rapport des modules, sans qu’il soit nécessaire de construire la droite hyperbolique pour avoir ses points idéaux.
Symétrie centrale par les nombres complexes
On a fait de même pour la symétrie centrale d’un point, avec la même remarque quant à l’utilisation du rayon du cercle \(Hz\). Pour l’illustration on a mis en évidence l’expression \(expB\) mais en pratique, la macro renvoie directement le point B, il n’y a donc pas d’objets intermédiaires pour cette macro.
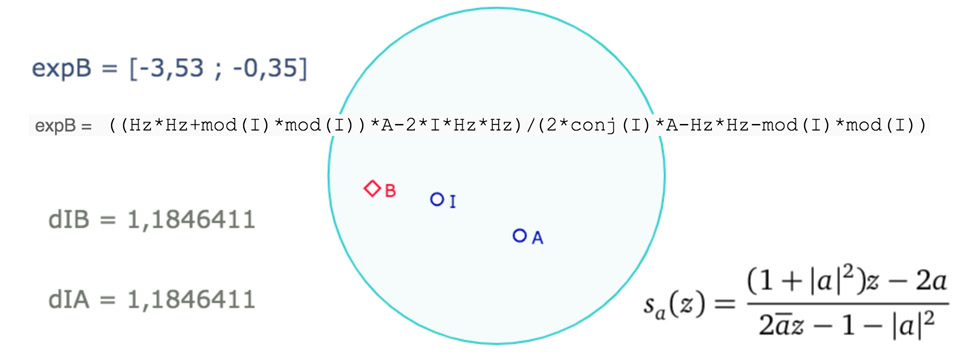
Le code interne de la macro : il n’y a bien qu’un point

Milieu et médiatrice
Par contre, on a choisit une démarche différente pour le milieu car, avec une construction semi-algébrique et semi géométrique, on construit en même temps le milieu de deux points et la médiatrice de ces deux points. Une construction purement géométrique de la médiatrice de deux points \(A\) et \(B\) serait l’intersection des deux cercles de centre un point passant par l’autre. On comprend que cette construction est assez lourde, en plus encore si elle devait être utilisée pour la construction du milieu de deux points. Voici une démarche algébrico-géométrique.
On rappelle que la distance de deux points \(A\) et \(B\) est (aussi) donnée par \(d(A,B) = \displaystyle \left\vert ln \left(\frac{AU}{AV} : \frac{BU}{BV}\right) \right \vert\).
L’égalité \(AB=2AI\) aboutit à \(\displaystyle \left( \frac{IU}{IV} \right)^2=\frac{AU.BU}{AV.BV}\).
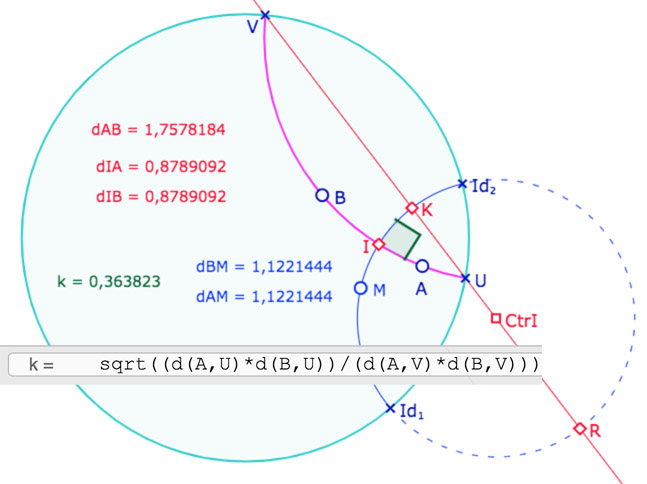
On a déjà utilisé la même démarche dans le disque KB : on sait que le lieu des points \(M\) tels que \(\displaystyle \frac{MU}{MV}=k\) est un cercle de diamètre \([KR]\) avec \(K=\displaystyle \frac{U+kV}{1+k}\) – entre \(U\) et \(V\) – et \(R=\displaystyle \frac{A-kB}{1-k}\). La différence avec le même thème dans KB est qu’ici il faut construire le cercle, le point I étant à l’intersection de ce cercle et de la droite hyperbolique \((AB)\).
Mais c’est pour cela que l’on a choisi cette méthode car le cercle pour construire le milieu de \(A\) et \(B\), est orthogonal à la droite (AB) – et au cercle horizon : en construisant ainsi le milieu on construit en même temps la médiatrice de \(A\) et \(B\).
Ancienne macro Symétrie Centrale
Pour l’anecdote, la même démarche était utilisée pour une macro précédente sur la symétrie centrale. Cela donnait cela :
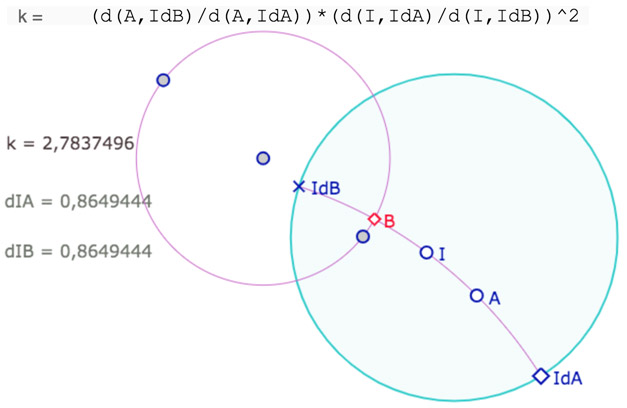
Et la macro associée contenait alors 14 objets intermédiaires – ce dont j’étais satisfait à l’époque – contre un seul objet avec la construction par les complexes ci-dessus.