Après plusieurs articles sur la présentation unificatrice des géométries hyperbolique et elliptique de Daniel Perrin, nous reprenons une approche plus classique, historique, des géométries non euclidiennes, explicitement construites autour de la notion de droites parallèles.
Historiquement, la géométrie hyperbolique a été découverte pratiquement à la même date par Lobatchevsky et Bolyaï vers 1826 pour les deux, avec une publication en 1829 pour le premier, et en 1832 pour le second. On sait aussi que Gauss avait déjà travaillé sur le sujet bien avant – depuis 1792 d’aprés une de ses lettres – et avait la conviction, autour de 1815, qu’une géométrie non euclidienne était aussi cohérente que la géométrie eucldieinne, mais avait choisi de ne pas publier sur le sujet.
Pourquoi Gauss n’a pas voulu publier ses résultats ? Voir le merveilleux papier de Bernard Ycart sur le sujet (à partir du paragraphe 13) ou écouter son audio.
L’histoire a surtout retenu le travail de Nicolas Lobatchevsky, approfondi pendant plus de deux décennies, depuis sa première « Géométrie imaginaire » de 1829 (en russe) jusqu’à sa version la plus aboutie de 1855 – traduite en français sous le terme « Théorie des parallèles » avec plusieurs publications intermédiaires. On se propose ici de présenter le travail de l’autre auteur, Janos Bolyaï, essentiellement parce qu’il s’est intéressé à la constructibilité des segments et des polygones réguliers, jusqu’à résoudre la question de la quadrature du cercle en géométrie hyperbolique. Son essai le signale en sous-titre.

Le mémoire de Bolyaï est construit en 43 paragraphes. Sa géométrie absolue est développée sur les 32 premiers paragraphe ensuite, il s’intéresse aux propriétés conduisant à des constructions hyperboliques. Par essence, ses constructions sont hyperboliques. Dans nos illustrations, nous allons souvent les simplifier car nous allons les construire « dans un modèle » : en particulier nous aurons accès aux points idéaux – les points à l’infini – qui sont, entre autres, les centres des horicycles, très utilisés par Bolyaï puisque les propriétés qu’il obtient proviennent de ce que l’horisphère – dont les droites sont des horicycles – est de structure euclidienne. On y reviendra plusieurs fois en détail.
Cet article propose d’illustrer, avec des figures dynamiques, la première partie du mémoire de Bolyai, jusqu’au § 32, pour voir, ensuite – dans un second article – comment il arrive à la quadrature du cercle : construire un carré d’aire égale à \(\pi\) et un cercle de même aire. Quand on ne dispose pas de modèle pour réaliser les constructions géométriques, construire signifie essentiellement prouver que les longueurs en jeu se réalisent par des intersections de droites et de cercles hyperboliques.
Les illustrations dynamiques sont faites dans le modèle du disque de Poincaré (DP). Pour manipuler les figures, il est préférable d’avoir lu avant les premières pages du menu DP, au moins cette introduction puis cette première page sur les droites.
Les notations de Bolyai sont surprenantes. Il ne donne pas de définitions précises comme Lobatchevsky, n’utilise pas les fonctions trigonométriques hyperboliques, et en définitive, son mémoire est plus difficile à suivre que celui de Lobatchevsky, essentiellement à cause de ses notations. Pourtant il contient des trésors d’ingéniosité, y compris pour trouver des théorèmes absolus nouveaux et significatifs. Pour arriver à ses fins en terme de constructibilité, Bolyai montre des propriétés originales sur les horicycles, et en particulier, il va transformer un arc d’horicycle en tangente d’un angle, donnant ainsi diverses constructions à travers lesquelles on peut voir une grande maîtrise de la géométrie étudiée : c’est la raison pour laquelle, nous allons explorer le mémoire de Bolyai, mais tout en conservant les notations standards dues à Lobatchevsky.
On notera que BolyaÏ travaille essentiellement sur des demi-droites parallèles (seconde notation ci-dessous), une approche clairement visionnaire : plus tard la même démarche sera à l’origine des « bouts » ou des « terminaisons » de Hilbert dans ses « Fondements ». Le texte de Bolyaï est concis et ses notations sont très spécifiques comme on peut le voir ci-dessous.

Pour ma part … parce que cela fait longtemps que je fréquente ces problématiques … c’est grâce à une ancienne présentation détaillée de Klauss Volkert dans ses deux articles « Et pourtant quelques uns sont quarrables » de l’Ouvert de l’IREM de Strasbourg (1996 – n°84 et 85 – articles téléchargeables ici et là) que j’ai pu découvrir en détail ce mémoire. Même si, bien entendu, les constructions historiques sont aussi présentes dans de nombreux ouvrages anglo-saxons sur les GNE, je voulais discrètement remercier ce défricheur qui m’a montré la voie …
La géométrie absolue de Bolyaï
Un autre argument pour présenter le travail de Bolyaï – et qui explique aussi parfois sa façon de rédiger est que Bolyai ne s’intéresse pas uniquement à une géométrie non euclidienne, comme Lobatchesky, mais au contraire, il est le premier à clairement définir ce qu’il appelle la géométrie absolue, c’est-à-dire la géométrie d’Euclide, sans référence au V° postulat (que Bolyai, note l’axiome XI suivant l’édition d’Euclide qu’il utilisait). Il dit précisément :
Nous désignerons par \(\Sigma\) le système de géométrie qui repose sur l’hypothèse de la vérité de l’axiome XI d’Euclide, et par \(S\) le système fondé sur l’hypothèse contraire. Tous les résultats que nous énoncerons, sans désigner expressément si c’est dans le système \(\Sigma\) ou le système \(S\) qu’ils ont lieu, devront être considérés comme énoncés d’une manière absolue, c’est-à-dire qu’ils seront donnés comme vrais, soit qu’on se place dans le système \(\Sigma\), soit qu’on se place dans le système \(S\).
Science absolue de l’espace – Bolyaï – § 15
Chez Bolyai, comme pour tous ses contemporains, le contraire de la vérité de l’axiome d’Euclide s’entend « toutes choses égales par ailleurs », c’est-à-dire avec toutes les autres demandes d’Euclide (postulats). Dans son travail, Saccheri, déjà, en 1733, rejetait définitivement ce qu’il appelait « l’hypothèse de l’angle obtus » car elle conduit clairement à une contradiction avec le caractère non borné des droites : il rejetait ainsi ce qui sera ultérieurement les possibilités de géométrie elliptique. Nous avons un peu la même chose ici, le contraire de l’axiome d’Euclide n’est pas « aucune parallèle ou au moins deux » mais bien seulement la seconde alternative. De même une autre demande du livre V sur les proportions conduisant à l’archimédie de \(\mathbb{R}\) est implicitement conservée.
Après bien d’autres, Bolyai utilise que de nombreuses propriétés sont absolues (les cas d’égalité des triangles, l’unicité de la perpendiculaire à une droite passant par un point donné, la caractérisation des médiatrices, celle des bissectrices). En pratique, dans les 48 propositions du livre I d’Euclide, les 28 premières propositions – et ensuite la 31° – n’utilisent pas le V° postulat. Ces propositions constituent donc un corpus que, depuis Bolyai, on appelle traditionnellement la géométrie absolue.
La définition de droites parallèles
Le mémoire de Bolyaï commence par la définition de droites parallèles et de l’angle de parallélisme, même s’il n’est pas défini comme tel.

Ce qui peut s’écrire, pour les parallèles, dans un vocabulaire contemporain :
Si la demi-droite \([AM)\) n’est pas coupée par la demi-droite \([BN)\) mais qu’elle est coupée par toute autre demi-droite \([BP)\) comprise dans l’angle \(\angle ABN\), on dira que \([BN)\) est parallèle à \([AM)\) et donc \((BN) // (AM)\).
Voici une illustration dynamique des deux parties de la proposition 1
On peut déplacer tous les points de la figure.
Cliquer sur la case à cocher pour la seconde partie de la proposition
Préférer ouvrir cette figure dans un nouvel onglet.
Même s’il paraît tout simple, ce premier paragraphe du mémoire de Bolyaï invite à plusieurs commentaires.
• Droites non connectables. Tout d’abord, la simplicité apparente de cette définition des droites parallèles ne l’est que par notre culture, véhiculée par l’histoire des mathématiques. En effet arriver à cette définition nécessite de franchir un véritable obstacle conceptuel auquel se sont confrontés tous les géomètres qui ce sont intéressés « au V° postulat », à savoir la connectabilité des droites : deux droites sont dites connectables si elles ont soit un point soit une perpendiculaire en commun. En géométrie euclidienne toutes les droites sont connectables car soit elles sont sécantes soit elles sont parallèles et ont une perpendiculaire commune, alors que la géométrie hyperbolique est le premier exemple de géométrie où des droites ne sont pas connectables et ce sont justement, les droites parallèles de cette géométrie. Cette nouvelle situation est à l’origine de ce qui peut être interprété comme une « surcharge cognitive » dans l’analyse qu’a proposé Saccheri en 1733 dans son ouvrage « Euclide lavé de toute tâche ».
En effet Saccheri avait bien montré que, « sous l’hypothèse de l’angle aigu », deux droites sont soit sécantes, soit asymptotes, soit ont une perpendiculaire commune. Et dans ce dernier cas, il avait même précisé « à partir de laquelle elles divergent», progrès majeur par rapport à ses prédécesseurs. Il avait aussi – conceptuellement bien sûr – fait la même figure que celle ci-dessus et montré la propriété qui définit la parallèle chez Bolyai et Lobatchevky. Mais la non connectabilité des droites était probablement juste inconcevable à cette époque. En effet, observant qu’alors les parallèles devraient avoir leur perpendiculaire commune « rejetée à l’infini », il a en a conclu à une contradiction. Et de conclure par cette phrase restée fameuse dans l’histoire des G.N.E. : « l’hypothèse de l’angle aigu est absolument fausse car cela répugne à la nature de la ligne droite ».
Lire ou écouter à nouveau Bernard Ycart à propos de Saccheri et de ses précurseurs.
• Angle de parallélisme. On retiendra plutôt l’approche de Lobatchevsky : quand, dans la figure précédente, les droites \((AM)\) et \((AB)\) sont perpendiculaires, alors l’angle \(\angle ABN\) est appelé angle de parallélisme et est noté, par Lobatchevsky, \(\Pi(AB)\). Avec cette notation, le cas euclidien correspond au cas où l’angle de parallélisme est constant et est un droit. Une propriété absolue de Euclide assure aussi que cet angle ne peut être supérieur à un droit. Le cas hyperbolique est un cas où l’angle de parallélisme est toujours inférieur à un droit, et dans ce cas il n’est pas constant.
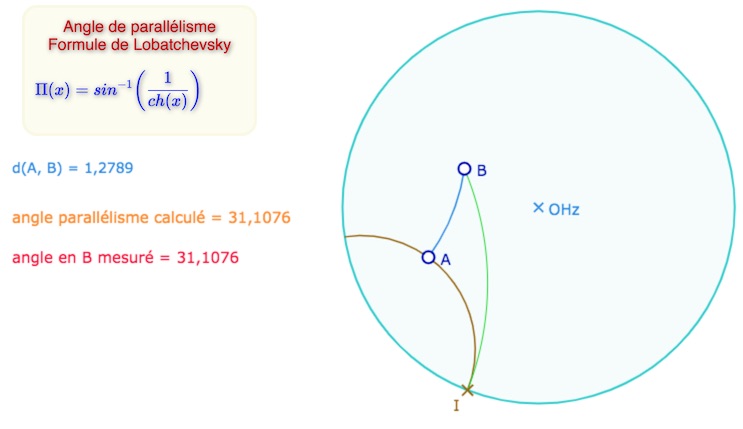
Angle de parallélisme, mesuré sur la figure et calculé par la formule de Lobatchevsy
Ouvrir la figure correspondant à cette illustration dans un nouvel onglet.
Dans cette figure et la suivante, les constructions sont faciles à réaliser car nous travaillons dans un modèle – et en particulier on a accès aux points à l’infini, ce qui n’a pas de sens quand on n’a pas de modèle. En particulier les calculs de Lobatchevsky et les constructions de Bolyaï sont intrinsèquement hyperbolique alors que nos constructions utilisent des possibilités propres du modèle.
Par exemple pour développer son approche de constructibilité, Bolyaï sera amené, en fin de mémoire, à construire, hyperboliquement donc, les angles de parallélisme \(\Pi(x)\) et les segments \(\Delta(u)\) où \(\Delta\) est la fonction réciproque de \(\Pi\). En effet \(\Pi\) est strictement décroissante, allant de \(\pi/2\) à 0 exclu quand le segment \(x\) varie de 0 à +\(\infty\). \(\Delta(u)\) donne la longueur du segment dont l’angle de parallélisme est \(u\) : \(\Pi(\Delta(u))=u\).
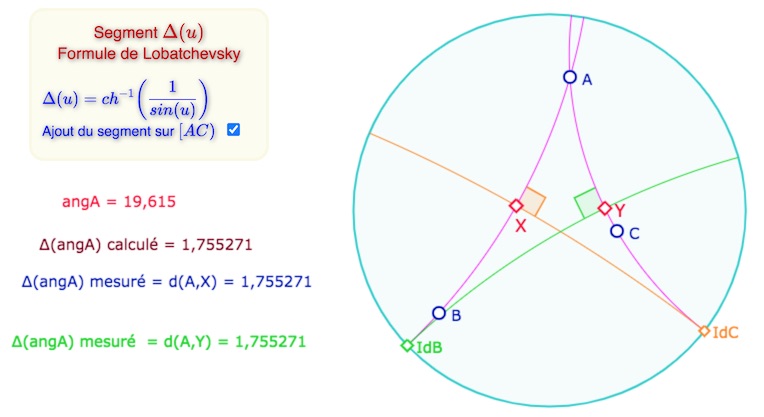
Là encore la construction de \(\Delta(BAC)\) est facile à réaliser depuis les points idéaux
\(Id_B\) ou \(Id_C\) : il suffit de prendre la perpendiculaire depuis ces points idéaux.
Ouvrir la figure associée à cette illustration dans un nouvel onglet.
Les constructions de Bolyaï sur ces deux concepts \(\Pi\) et \(\Delta\) ouvrent le second article sur ce mémoire.
Définition des horicycles et des horisphères
Bolyaï va aborder la question de la constructibilités des segments hyperboliques sur la base d’arcs d’horicycles. Commençons par voir comment il présente les horicycles. Chez lui, ce n’est pas un « cercle-limite » comme pour Lobatchevsky, mais une courbe basée sur la propriété angulaire suivante :
Propriété des parallèles (§ 5) : Étant données deux parallèles \([An)\) et \([Bm)\), il existe un point \(F\) sur \([An)\) tel que les angles \(\angle nFB\) et \(\angle mBF\) sont égaux.
Voici une version dynamique adaptée au contexte où l’on dispose des points à l’infini. On a donc légèrement modifié les hypothèses en parlant de droites au lieu de demi-droites.
Dans cette figure, déplacer les points \(A, n, B\). Remarquer alors que le point \(F\) peut être, sur \((An)\),
mais en dehors de la demi-droite \([An)\), d’où la modification à la marge des hypothèses.
Préférer ouvrir cette figure dans un nouvel onglet
Rappelons toutefois que le fait d’utiliser systématiquement des demi-droites a véritablement du sens, cela permet de prendre en compte, sans le nommer, « le bout » des droites parallèles, c’est-à-dire, le point idéal \(I\) dans la figure ci-dessus. En effet, le parallélisme hyperbolique n’est pas une relation d’équivalence, alors que les droites parallèles « de même terminaison » sont en pinceau comme on va le voir un peu plus loin.
Définition des horisphères et des horicycles (§ 11)
Dans ce paragraphe, et les suivants, \(F\) ne désigne plus le point du § 5 mais désormais un ensemble de l’espace, ce que le traducteur a cru bon préciser. Mais ce point (l’ancien \(F\)) reste essentiel dans la construction.

Les notes sont du traducteur Jules Houel qui a aussi traduit Lobatchesvky …
ainsi que Beltrami avec qui il a entretenu une longue correspondance (publiée).
Reprenons la partie horicycle, en se limitant au plan, dans un premier temps. On se donne une droite \([An)\) et toutes ses parallèles \([Bm)\) – donc dans le plan seulement. Il existe donc un point \(H\) (l’ancien \(F\)) tel que les angles \(\angle nHA\) et \(\angle mAH\) soient égaux. L’horicycle, la courbe \(L\) du texte, est le lieu des points \(H\) quand \([Bm)\) décrit toutes les parallèles à \([An)\).
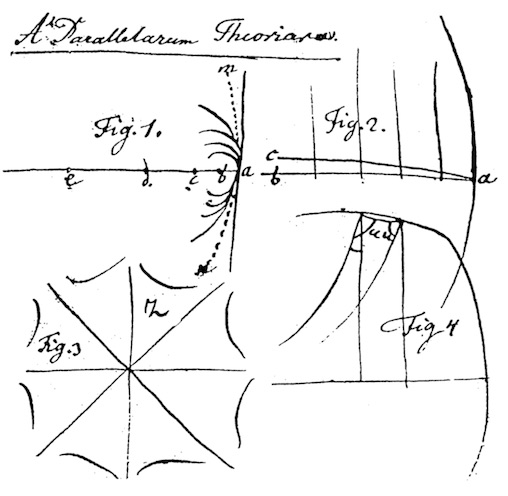
« On sait par des esquisses publiées par Stäckel que Bolyaï avait l’idée de ces lignes assez précises »
mentionné par Klauss Volkert dans la seconde partie de son article
Dans la figure suivante, les droites parallèles sont données par un point du plan hyperbolique et leur point idéal commun \(I\).
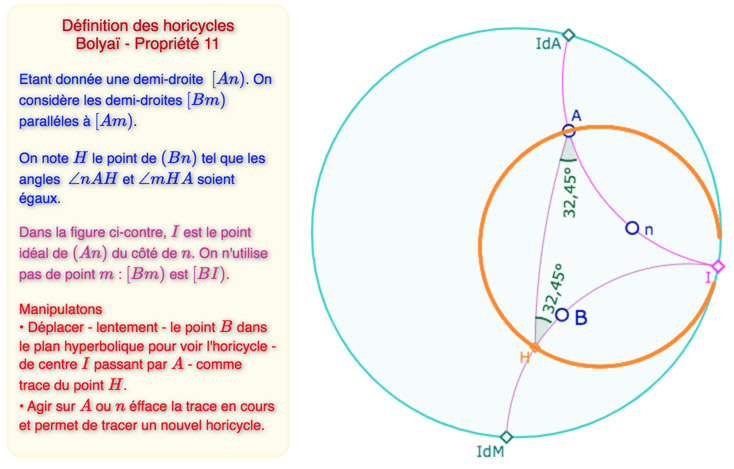
Définition de Bolyaï des horicycles : lieu du point \(H\) quand \([Bm)\) est parallèle à \([An)\).
Lancer la figure associée à l’illustration ci-dessus dans un nouvel onglet.
La figure précédente, très proche de la définition de Bolyaï, a l’inconvénient de ne produire qu’une trace. Cela est dû uniquement au fait que le point \(B\) est un point libre : on ne peut pas prendre de lieu en fonction de \(B\). On peut refaire la figure, encore proche de la définition, mais utilisant d’autres outils du modèle.
On peut agir sur \(o_{BI}\) pour voir \(H\) se déplacer sur l’horicycle tracé,
et sur \(A\) ou \(n\) pour modifier l’horicycle – car cela change le point \(I\).
Préférer ouvrir cette figure dans un nouvel onglet.
Au paragraphe suivant (§ 12), il montre que « toute parallèle à \([An)\) est aussi axe de la courbe \(L\)« . Le lien – pour nous – avec la définition de Lobatchevsky des horicycles est alors immédiat.
On notera que l’on a utilisé les marques standards du logiciel pour les angles hyperboliques (H-angles) et donc – comme ce sont les mesures des tangentes – elles paraissent plus petites que les angles mais ce sont bien les valeurs des H-angles.
Préférer ouvrir cette figure dans un nouvel onglet.
Bolyaï montre ensuite les propriétés usuelles de l’horicycle dont celle-ci qui, dans certaines présentations contemporaines, est une définition alternative des horicycles.
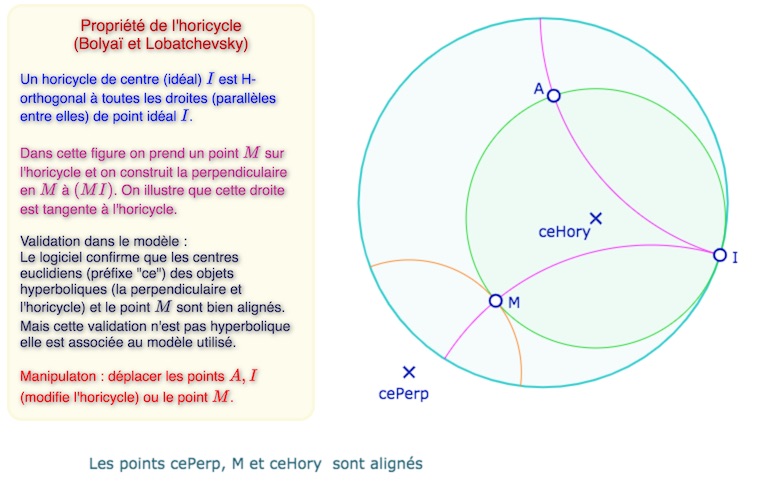
Lancer la figure associée à cette illustration dans un nouvel onglet
Les horisphères – les « courbes \(F\) «
Tout d’abord signalons que, si Bolyaï ne précise pas – pas tout de suite – ce que sont ces courbes \(L\) et \(F\), c’est que nous somme au § 11 et qu’au § 15 – mentionné en début d’article – il va séparer la géométrie euclidienne (système \(\Sigma\)) de la (future) géométrie hyperbolique (système \(S\)). Il montre alors (§ 17) que, dans \(\Sigma\), la courbe \(L\) est une droite et la surface \(F\) est un plan.
Nous nous intéressons désormais au système \(S\), donc aux horisphères. Il s’agit de faire tourner un horicycle autour de son axe de définition. Dans le modèle du disque de Poincaré, une horisphère est représentée par une sphère épointée par le point idéal, centre de l’horisphère, noté \(I\) dans les illustrations suivantes.
La droite passant par deux points \(A\) et \(B\) d’une horisphère de centre \(I\) est l’horicycle de même centre passant par ces deux points.
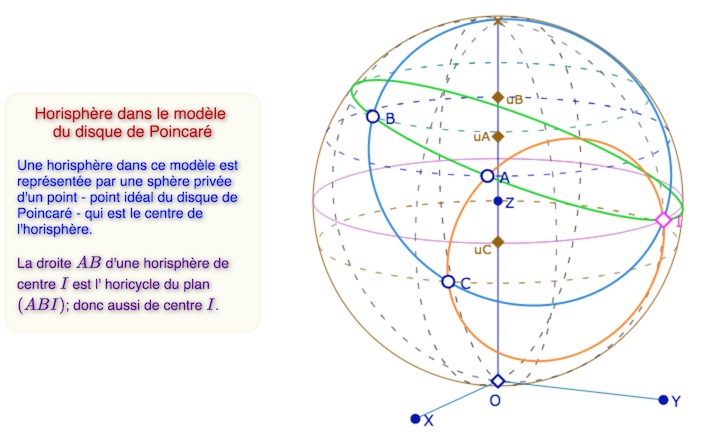
Dans les figures suivantes sur les horisphères, le point idéal est toujours le point [0, 1, 1], les points de base \(A, B, C\) se manipulent par leur latitude (les points \(u_A, u_B, u_C\)) et directeurs sur les parallèles définies par ces latitudes.
Cet horicycle est aussi l’intersection de l’horisphère avec le plan hyperbolique le contenant. Bolyaï étudie alors la géométrie de l’horisphère, et par les angles entre les plans hyperboliques. On arrive alors au § 21 :
Deux lignes \(L\), \(\overrightarrow{ap}\) et \(\overrightarrow{bd}\), dans une même surface \(F\), faisant avec une troisième ligne de \(F\), savoir, avec \(ab\), des angles intérieurs dont la somme est < \(2R\), se rencontreront.
Bolyaï – « La science absolue de l’espace – § 21 (première partie)

Lancer la figure associée à cette illustration dans un nouvel onglet.
Il résulte de là que l’axiome XI et toutes les conséquences que l’on en déduit en géométrie et en trigonométrie (plane) sont vraies d’une manière absolue dans \(F\), les lignes \(L\) jouant le rôle de lignes droites. Par conséquent, les fonctions trigonométriques seront prises ici dans le même sens que dans le système \(\Sigma\); et les circonférences du cercle tracé dans \(F\) et ayant pour rayon une portion d’une ligne \(L\) égale à \(r\) aura pour longueur \(2\pi r\), et de même son aire sera \(\pi r^2\)« .
Bolyaï – « La science absolue de l’espace – § 21 (deuxième partie)
Lobatchevsky était arrivé au même résultat : la géométrie des horisphères est euclidienne.
Exemple d’illustration 1 : les angles d’un triangle

Dans ces figures, on déplace la sphère par le point \(O\),
on tourne la sphère en mode consultation : aucun outil sélectionné.
(Les angles sont calculés directement sur la surface)
Lancer la figure associée à cette illustration
Exemple d’illustration 2 : parallèle à une droite passant par un autre point et parallélisme
Dans ces figures sur l’horisphère, les points sont manipulables par leurs latitudes \(u_X\) et les points \((X=A, B, C)\) (ou \(D\) ci-dessous) eux-mêmes. La figure suivante construit la parallèle à \((AB)\) passant par \(C\) et celle passant par \(D\). Alors ces deux dernières droites sont aussi parallèles … ce qui est une propriété euclidienne : le parallélisme est une relation d’équivalence.
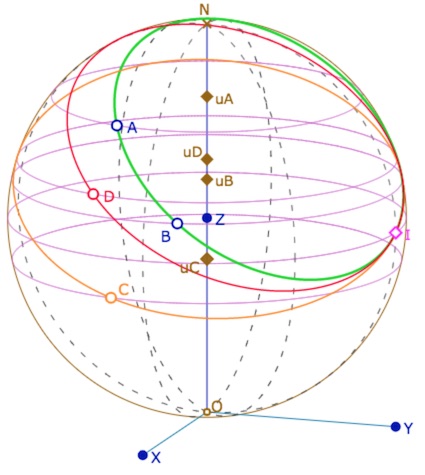
Lancer la figure associée à cette illustration
Exemple d’illustration 3 : le théorème des milieux dans un triangle
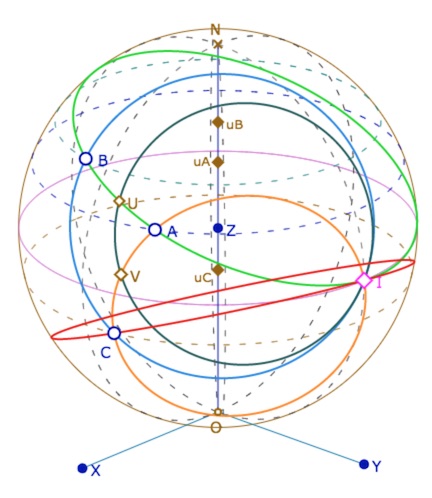
\(U\) et \(V\) sont les milieux de \([AB]\) et \([AC]\).
La droite \((UV)\) est parallèle à \((BC)\)
Lancer la figure associée à cette illustration
Autre point de vue déjà présenté sur le site
Dans ces dernières figures on a utilisé un point fixe (le point [0, 1, 1]) comme point idéal \(I\) sur une horisphère toujours de rayon euclidien 1 – pour simplifier certains calculs. Le choix de ce point est en référence au même point dans les figures reliant la pseudosphère du modèle de Klein-Beltrami, pour de futurs échanges. entre ces différents modèles.
Mais dans ce site on a déjà présenté plusieurs autres figures (Feuerbach entre autres) dans une autre présentation des horisphères, où le point idéal est le pôle Nord de la sphère. On y a par exemple présenté la construction de Malfatti dans cette configuration

Construction de Malfatti dans une horisphère de point idéal le pôle nord
Accéder à la page de menu Modèle euclidien 3D borné
De plus un article intitulé Manipuler sur l’horisphère propose de faire soi-même de telles figures à partir de nombreuses macros placées dans une figure de base.
Considérations techniques pour la réalisation de macros avec le point idéal \(I\)
Si un lecteur avait envie de reprendre les macros de l’article précédent pour l’adapter aux figures avec le point idéal \(I\), voici quelques informations préliminaires sur les constructions effectives sur la sphère. En pratique on adapte les calculs de la page « Modèle euclidien 3D borné » à la projection sur le plan \((xOz)\). On obtient \(\left\lbrace \begin{array}{1} X= \displaystyle \frac{2x}{1-y}\\ Z=1+\displaystyle \frac{2(z-1)}{1-y}\end{array}\right.\)
Pour le retour sur la sphère, on utilise

Les horicycles concentriques
Parce que les horisphères sont euclidiennes et que leurs droites sont des horicycles, le théorème de Thalès sur une horisphère aboutit à un procédé de type « Thalès hyperbolique » sur les rapports d’arcs d’horicycles concentriques (qui proviennent de droites parallèles sur l’horisphère).
On commence, pour les premières définitions, avec une version dynamique illustrant la propriété obtenue au § 22
Étant donné un horicycle \(H\), par exemple celui de centre \(I\) passant par \(C\),
cette première propriété montre aussi que la ligne équidistante à \(H\) passant par un point A,
est l’horicycle \(H’\) de même centre que \(H\), passant par \(A\).
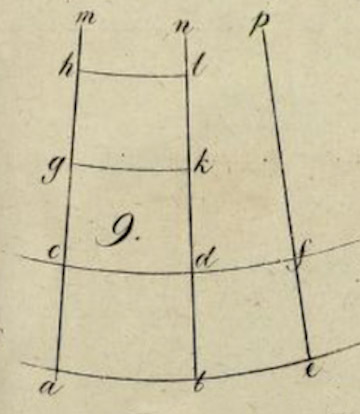
L’illustration associée aux paragraphes 22 et 23. Elle justifie le X>1 (voir plus loin)
Le « Thalès hyperbolique » est évoqué au paragraphe suivant. Voici une copie d’écran de la même figure que ci-dessus, mais présentant aussi cette propriété (§ 23) :

Les définitions des expressions \(X\) et de \(x\)
Ouvrir cette figure dans un nouvel onglet.
Dans le paragraphe suivant, § 24, Bolyaï observe que, dans \(\Sigma\), la géométrie euclidienne, on a toujours \(X=1\), car les horicycles étant des droites, un quadrilatère comme \(ACDB\) (de la figure ci-dessus) est simplement un rectangle. Sinon, dans \(S\), on a \(X>1\), et, pour deux valeurs \(x, y\), il montre qu’alors \(Y=X^{\frac{y}{x\displaystyle }}\).

Illustration 3D du cas X=1
Ouvrir cette figure de l’horisphère dans un nouvel onglet
Remarque : \(X>1\) car, dans l’illustration originale montrée plus haut, on voit que Bolyaï utilise toujours des demi-droites et donc, contrairement à la figure dynamique proposée, \(C, D, F\) sont sur les demi-droites parallèles (dans la figure de point idéal \(I\)) d’origine \(A, B, E\).
Puis arrive ce qui reste le plus célèbre résultat absolu de Bolyaï (vrai aussi bien dans \(\Sigma\) que dans \(S\)) :
Dans tout triangle rectiligne, les circonférences de rayons égaux aux côtés sont entre elles comme les sinus des angles opposés
« La science absolue de l’espace » – Bolyaï – § 25
(bien entendu, montré par des arguments géométriques sans encore savoir calculer les \(S\)-circonférences.)
Une première conséquence, qui explique peut-être, du moins en partie, le titre du mémoire « science absolue de l’espace » est le résultat du § 26 qui se termine ainsi :

Mais ce théorème du §25 permet surtout le calcul du rapport \(X\).
Expression trigonométrique de \(X\)
Avant le calcul proposé ci-dessous, Bolyaï utilise § 25 pour montrer, en § 27, un résultat analogue entre une droite et ce que nous appelons « son équidistante », mais qui est définie par Bolyaï à partir de considérations d’angles (comme pour les horicycles). Bolyaï parle alors de « courbe parallèle » à la droite.
Nous arrivons au § 28 :
Dans la manipulation, respecter le fait que les points \(C, D, F\) sont sur les demi-droites de point idéal \(I\) d’origine, respectivement, \(A, B, E\), sinon la partie « Anticipation » comprendrait une erreur de signe.
Préférer ouvrir cette figure dans un nouvel onglet.
Cette relation est fondamentale. Elle sera utilisée dans deux directions, le cas particulier de la section précédente, puis ultérieurement (prochain article) pour le calcul effectif de la longueur de l’arc d’horicycle. Commençons par le cas particulier qui permet d’aborder l’angle de parallélisme.
Calcul de l’angle de parallélisme
Le paragraphe suivant (§ 29) traite de ce cas particulier important où l’angle \(u\) est droit. On reprend les notations standards, celles de Lobatchevsky, comme le mentionne le traducteur lui-même dans cette note
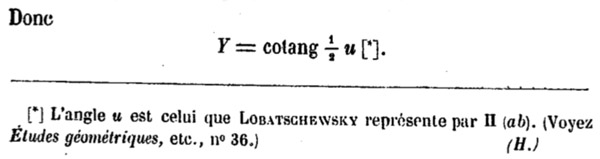
On peut déplacer les trois points de la figure
Préférer ouvrir cette figure dans un nouvel onglet.
La formule montrée par Bolyaï s’écrit maintenant \(tan \left( \frac{\Pi(x)}{2} \right) = e^{-x}\).
Autres expressions équivalentes (avec une écriture contemporaine)
\(\displaystyle sin\left( \Pi(x)\right)=\frac{1}{ch(x)} \quad tan \left( \Pi(x)\right)=\frac{1}{sh(x)} \quad cos \left(\Pi(x)\right)=th(x)\)Périmètre d’un cercle
Le paragraphe suivant (§30) montre qu’un cercle de rayon \(r\) a pour périmètre \(2\pi sh(r)\).
Trigonométrie hyperbolique
dans un triangle
Ainsi, ayant montré (§ 25, sur l’ horisphère) la proportionnalité entre les périmètres des cercles de rayon un côté du triangle et le sinus de l’angle opposé, après avoir établi le périmètre du cercle (§30), Bolyaï arrive rapidement à la relation des sinus de la géométrie hyperbolique :
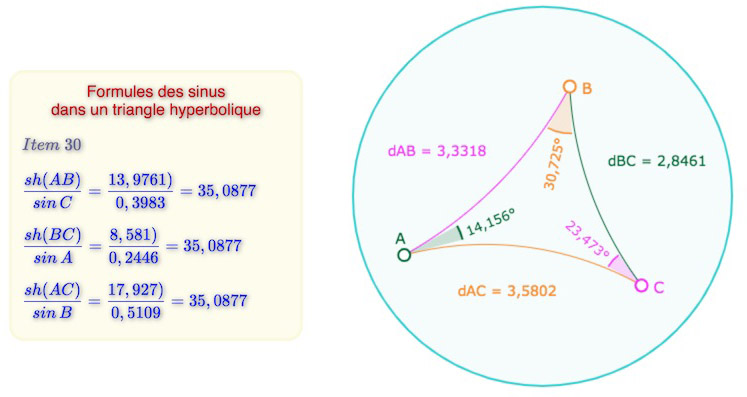
Les calculs du § 31 – Première partie
Ouvrir la figure associée, pour manipulation, dans un nouvel onglet
Il poursuit par les relations entre les côtés et les angles. En effet, comme il n’y a pas de similitude, il n’y a qu’un seul triangle ayant trois angles donnés, et donc on peut déterminer un angle en fonction de trois côtés. Ci-dessous, transcrit avec les notations usuelle car Bolyaï n’utilise pas les lignes trigonométriques hyperboliques.
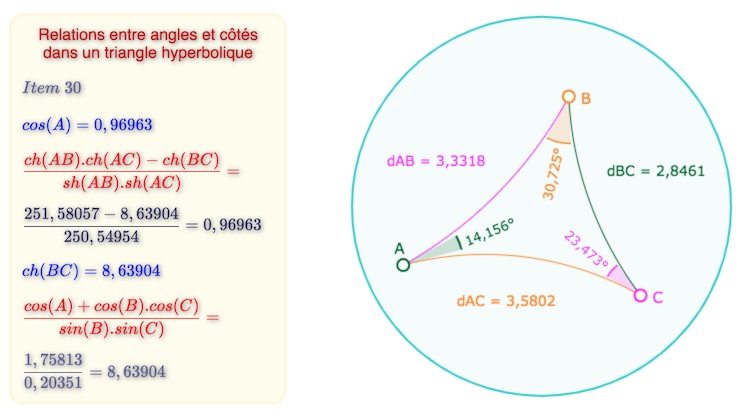
Expression d’un angle en fonction des trois côtés et d’un côté en fonction des trois angles
(§ 31 – Seconde partie)
Ouvrir la figure associée à cette illustration, dans un nouvel onglet.
Pythagore hyperbolique et autres relations trigonométriques
Relations qui dans le cas du triangle rectangle – figure fondamentale pour les constructions ultérieures (du prochain article) – se simplifient et donnent :
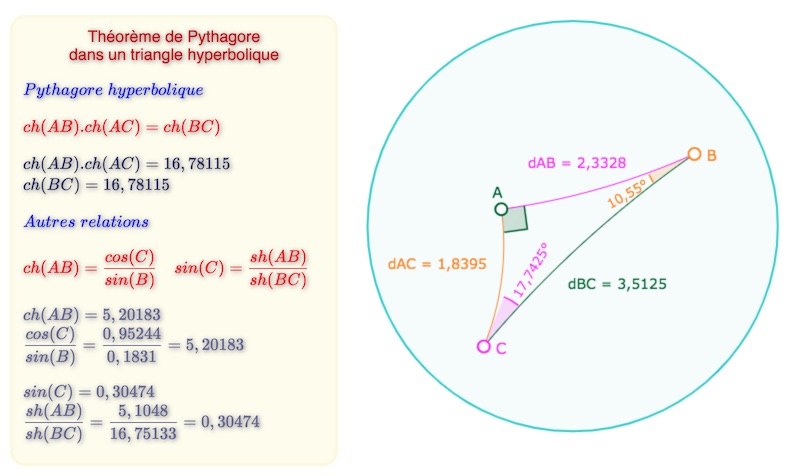
Ouvrir la figure associée à cette illustration, pour manipulation, dans un nouvel onglet.
Dans un triangle \(ABC\), rectangle en \(A\), outre les trois relations présentées dans la figure précédente, on a aussi les relations :
\(\displaystyle cos(C) = \frac{th(AC)}{th(BC)} \quad et \quad tan(C) = \frac{th(AB)}{sh(BC)}\)Aire du disque
Enfin, avant d’aborder la deuxième partie de son mémoire (constructibilité des côtés et quadrature du cercle), Bolyaï montre un dernier résultat sur le cercle.
§ 32 – L’aire du disque de rayon \(r\) est \(\displaystyle 4\pi \, sh^2\left( \frac{r}{2} \right)\)
Le manuscrit en Bolyaï en français
On peut télécharger ci-dessous la traduction du manuscrit par Jules Houel ainsi qu’une planche des illustrations originales, car elles sont illisibles sur le document proposé.
Merci à Bernard Ycart de m’avoir fourni le lien de cette planche d’illustrations
Article suivant : constructibilité des segments et quadrature du cercle
et ses applications avec le thème « cercles de pavages » avec des belles figures dynamiques d’illustration.