On poursuit l’illustration du travail de Daniel Perrin sur les modèles projectifs munis d’une forme quadratique non dégénérée. Ce quatrième article est consacré à un nouvel invariant, mis en évidence par Daniel Perrin dans son chapitres 4 . On rappelle que l’objectif de ces pages sur KE–KH est d’illustrer dynamiquement les propriétés de ces modèles sans vraiment entrer dans l’argumentaire mathématique pour lequel nous renvoyons au texte de Daniel Perrin.
Avant d’aborder cet article, il convient d’avoir lu, bien entendu, le premier article de présentation, sur les points et droites de KE et KH, ainsi que l’article présentant les invariants que sont les longueurs et les angles. Pour les constructions nous allons utiliser un compas, et donc des cercles. On peut se limiter au simple fait de savoir que, dans ces deux modèles, les cercles sont représentés par des coniques euclidiennes. On peut aussi parcourir le premier article sur les cercles. La référence est toujours le PDF DPPartie4 de ce livre de Daniel Perrin, en cours de publication. Les numéros des pages mentionnées sont celles de ce fichier.
Spin de trois points – Première application :
le troisième cas d’égalité des triangles
… C’est ce que vont montrer les divers cas d’isométrie des triangles. Comme en géométrie euclidienne, il s’agit de savoir à quelle condition trois points peuvent être envoyés sur trois autres par un élément de PO(q) et là encore il suffira (presque!) de se donner trois paramètres (longueurs ou angles). Le mot “presque” renvoie à la présence du spin. En vérité, dans le cas du corps des nombres réels, les cas d’isométrie peuvent être énoncés sans référence au spin en utilisant les angles de demi-droites, à l’exception du troisième cas d’isométrie, celui qui ne fait intervenir que les longueurs. Les formules d’Al-Kashi permettront de faire le lien entre ces divers résultats.
Daniel Perrin – Partie 4 – Page 152
La donnée des trois longueurs \(I(A,B), I(A,C), I(B,C)\), dans le cas général – et plus particulièrement dans KE – ne détermine un triangle « qu’à un signe prés ». Il faut donc un invariant supplémentaire qui rende compte de cette question de signe. Daniel Perrin propose alors la définition suivante :
Pour trois points non isotropes \(A, B, C\) on appelle spin de ces trois points le nombre
\(S(A, B, C) = \displaystyle \frac{\varphi(A,B)\varphi(B,C)\varphi(A,C)}{q(A)q(B)q(C)}\)
Comme le spin de trois points est indépendant de l’ordre de ces points, on parlera aussi bien du spin du triangle \(ABC\) … même quand ces trois points sont alignés.
On a \(S(A, B, C)^2 =I(A,B), I(A,C), I(B,C)\) de sorte que la donnée des longueurs détermine le spin au signe près. Daniel Perrin précise alors :
L’appellation, qui fait référence au spin des particules en physique, veut justement évoquer cette ambiguïté de signe. Dit savamment, le phénomène, au moins en géométrie elliptique, c’est que l’application qui à un triangle associe les longueurs de ses côtés est un revêtement de degré 2, autrement dit que la donnée des longueurs des côtés ne détermine pas un triangle, mais deux.
Daniel Perrin – Partie 4 – Page 153
La première application que donne Daniel Perrin est le cas d’égalité des triangles ayant trois côtés deux à deux de mêmes longueurs.
Troisième cas d’égalité des triangles – version longueurs
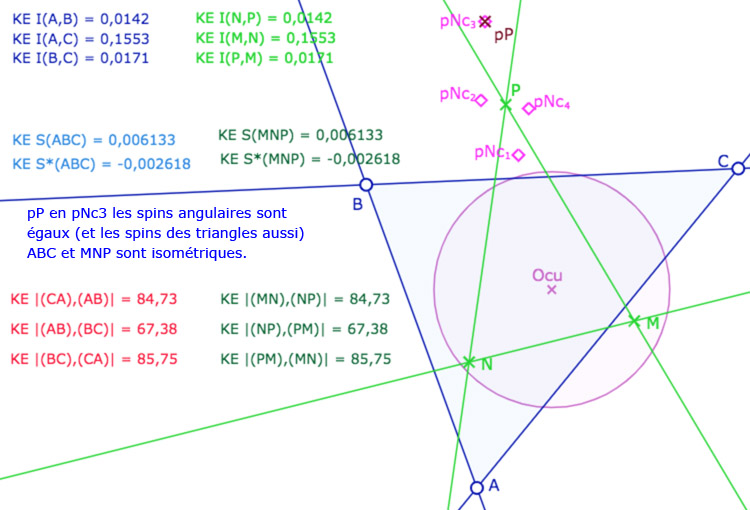
D’une manière générale, si deux triangles ont leurs côtés de même longueur et ont même spin, alors ils sont isométriques (« sont égaux » avec le vocabulaire d’Euclide).
Bien entendu, il y a, de base, la condition supplémentaire que les points doivent avoir même signe [pour la forme quadratique associée]. Cela n’induit une contrainte que pour pour KH, les points doivent être tous les trois soit à l’intérieur du cercle unité soit à l’extérieur.
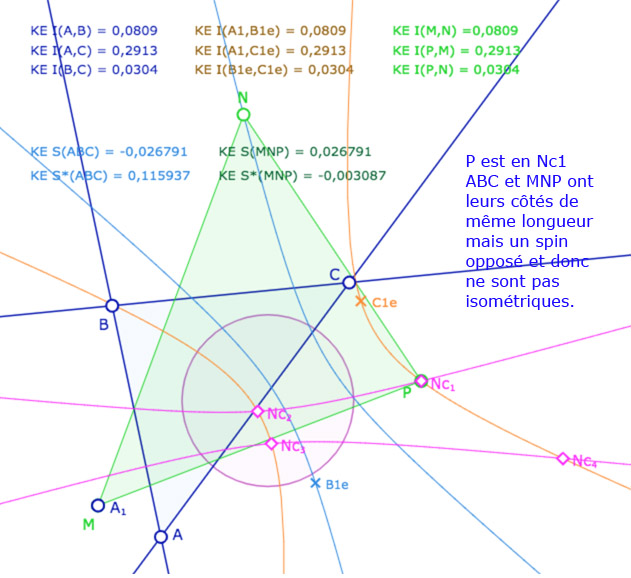
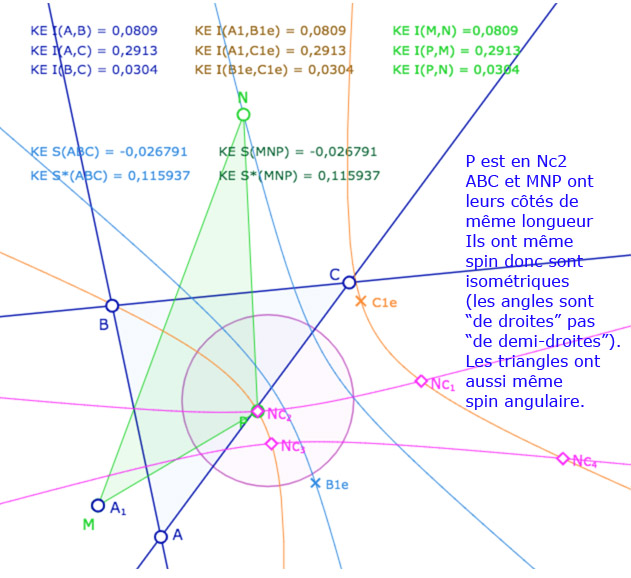
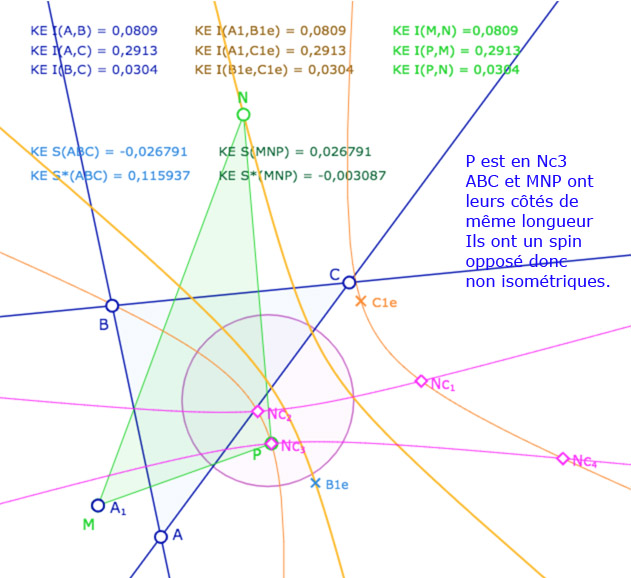
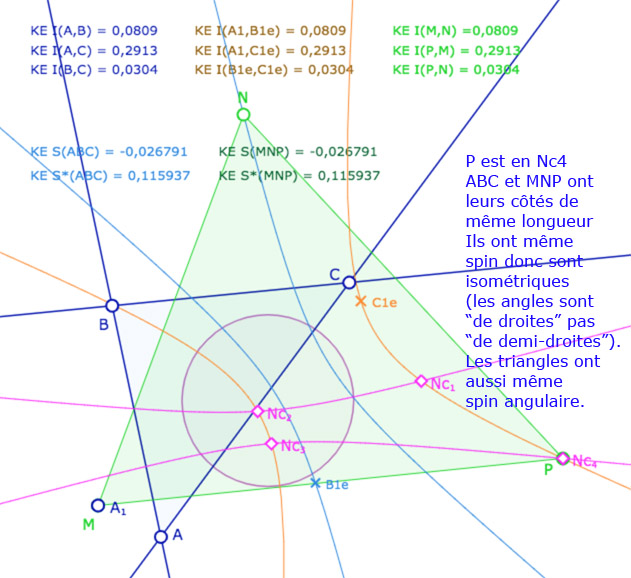
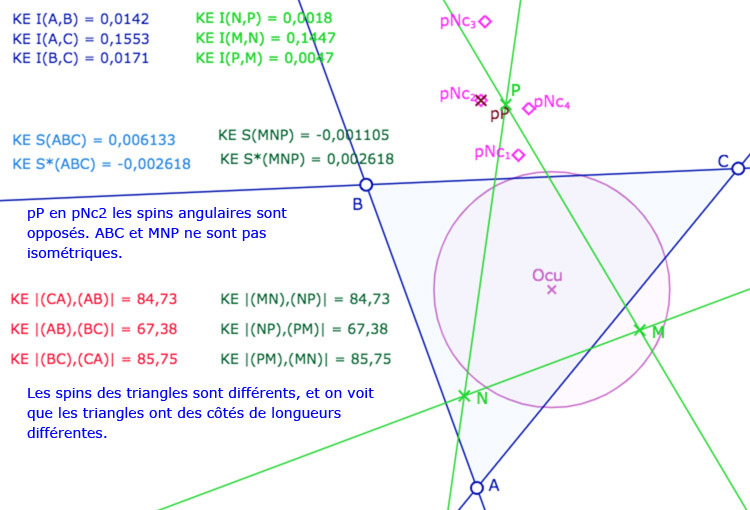
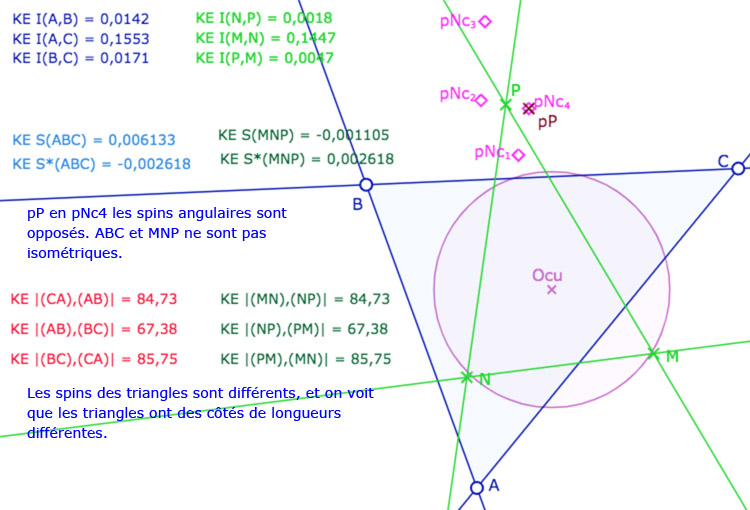
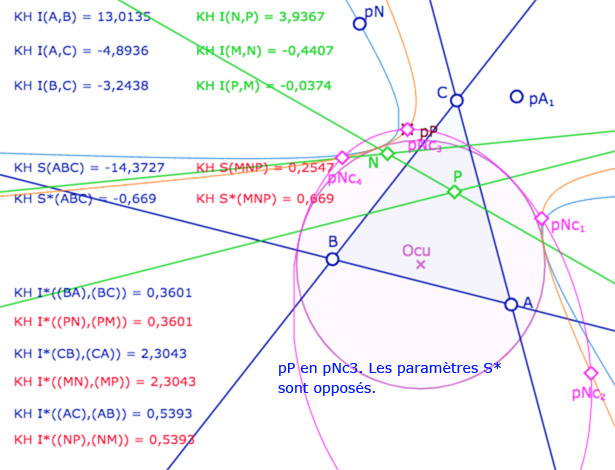
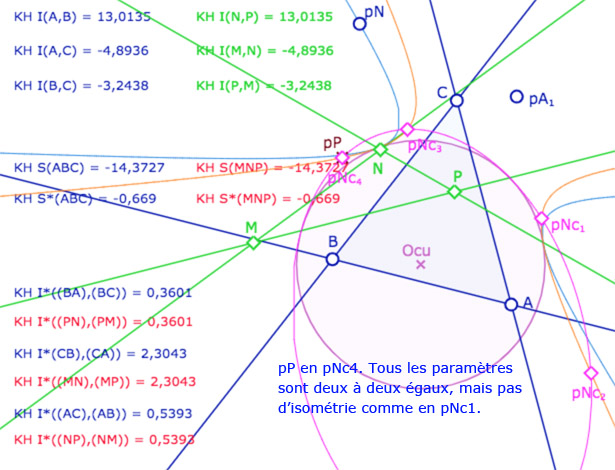
Avant de poursuivre sur les autres applications, donnons une première illustration dynamique, dans les deux modèles KE et KH, pour vérifier que (même dans KH) que deux triangles peuvent avoir des côtés de même longueur mais pas le même spin.
Illustration de ce troisième cas d’égalité
A – Dans le modèle elliptique KE
On se donne un triangle \(ABC\) (trois droites), on calcule la longueur entre les sommets (en bleu). On se donne ensuite un point \(A_1\). Depuis ce point, par une des médiatrices de \(A\) et \(A_1\), on construit \(B_{1e}\) et \(C_{1e}\) les images de \(B\) et \(C\). Par construction les deux triangles \(ABC\) et \(A_1B_{1e}C_{1e}\) sont isométriques. On vérifie, par le calcul, que l’on a bien \(A_1B_{1e}=AB, A_1C_{1e}=AC\) et \(B_{1e}C_{1e}=BC\) (en marron).
On construit alors le cercle de centre \(A_1\) passant par \(B_{1e}\), c’est la conique en bleu clair : c’est l’ensemble des points \(N\) tel que \(A_1N=AB\). De même, avec le cercle de centre \(A_1\) passant par \(C_{1e}\), c’est la conique en orange. C’est l’ensemble des points \(P\) tel que \(A_1P=AC\).
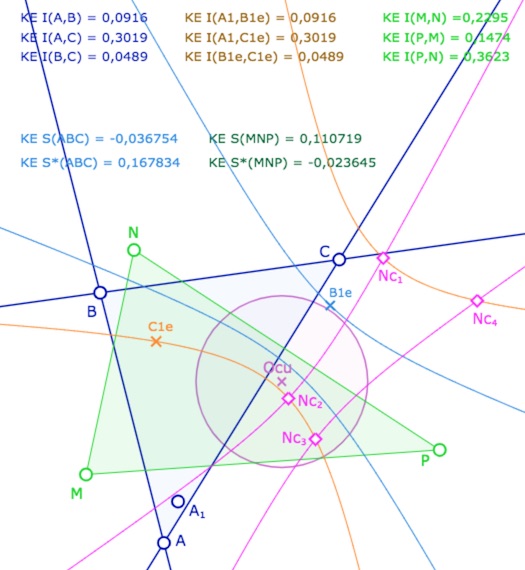
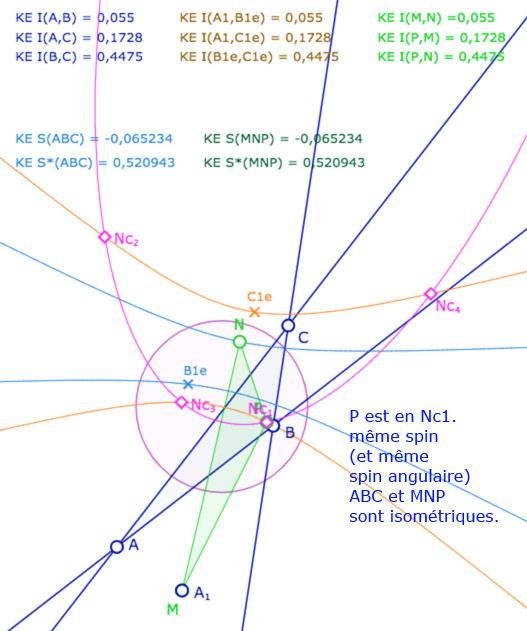
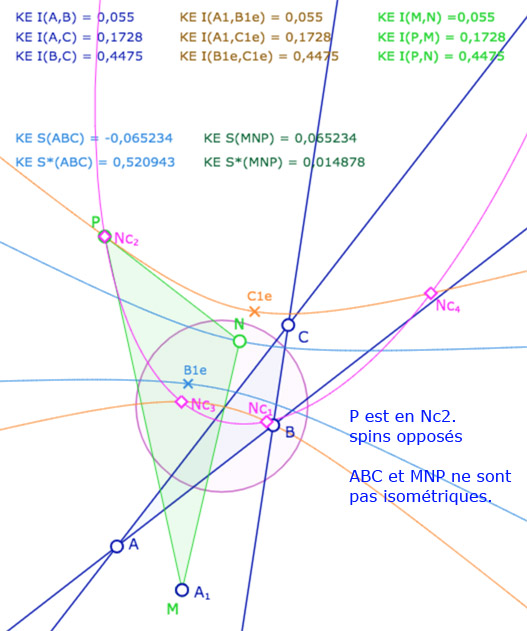
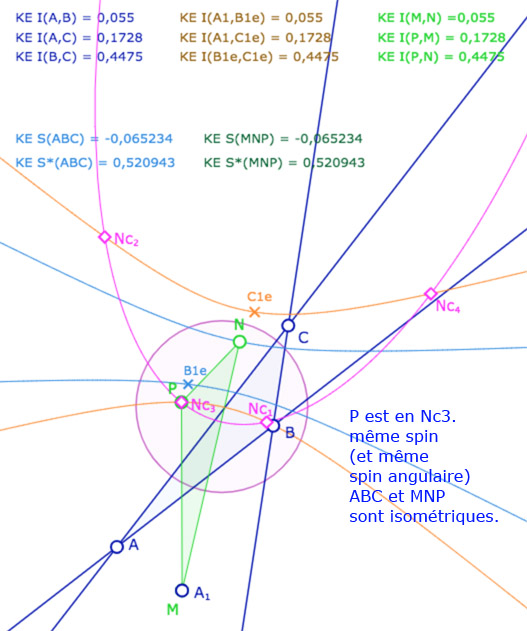
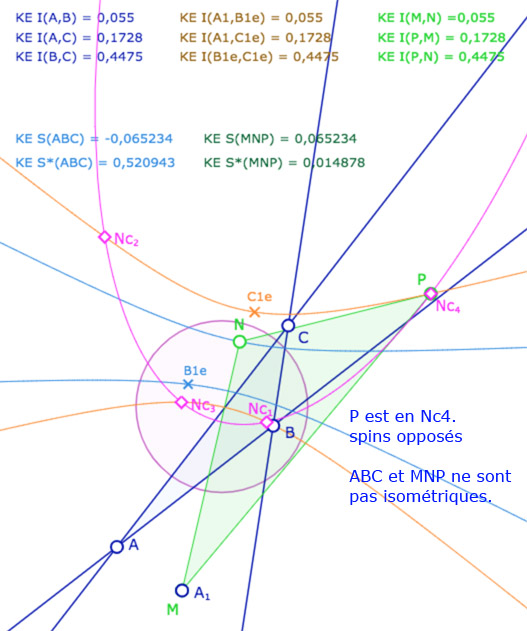
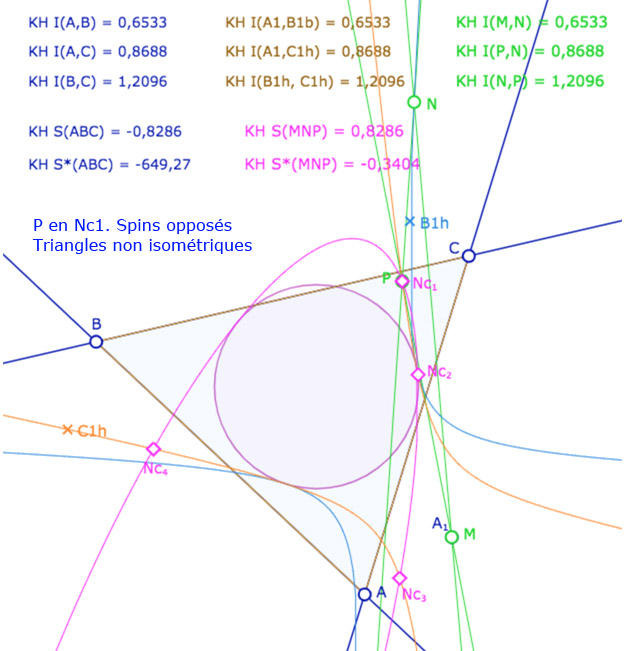
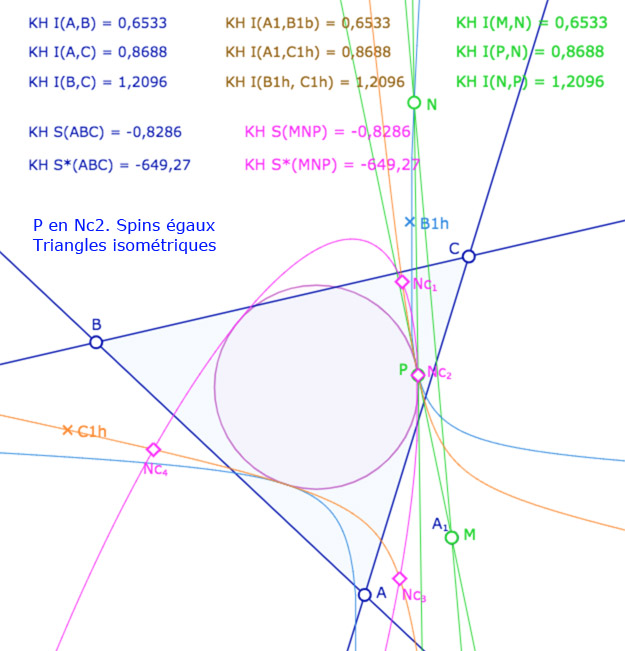
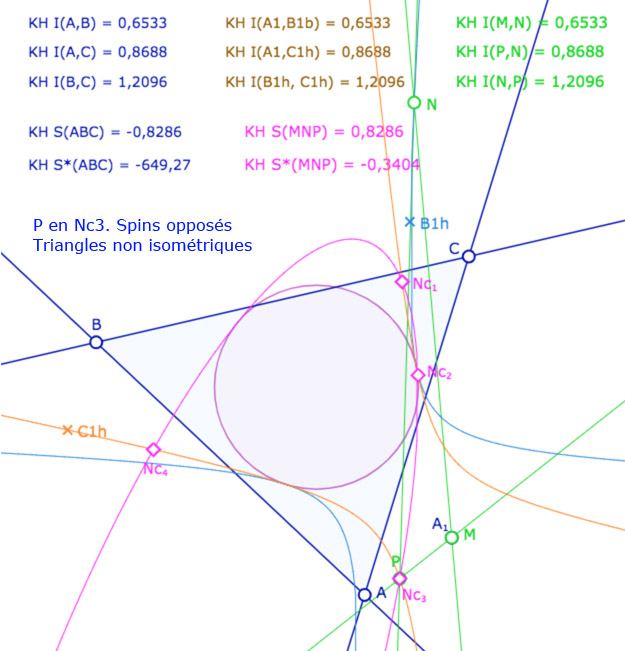
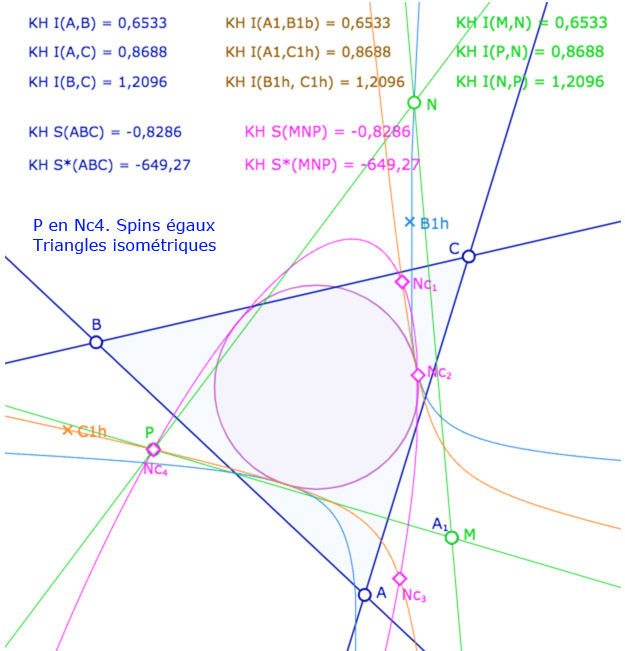
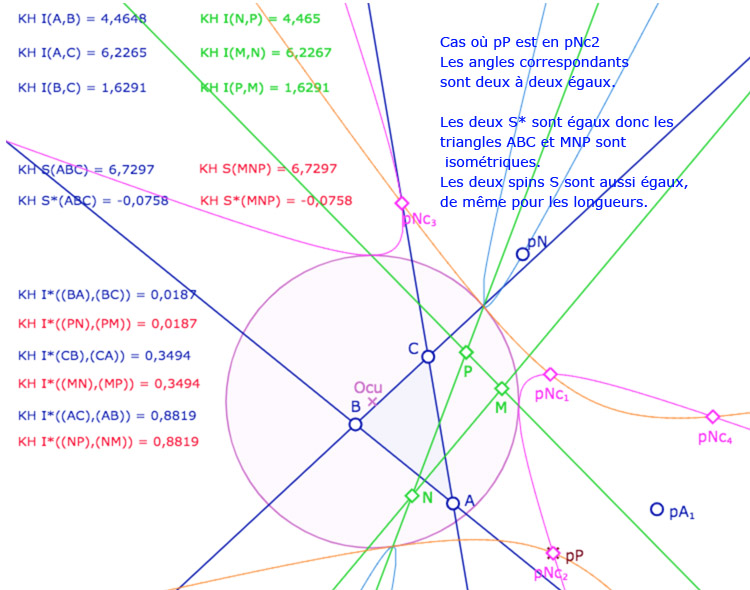
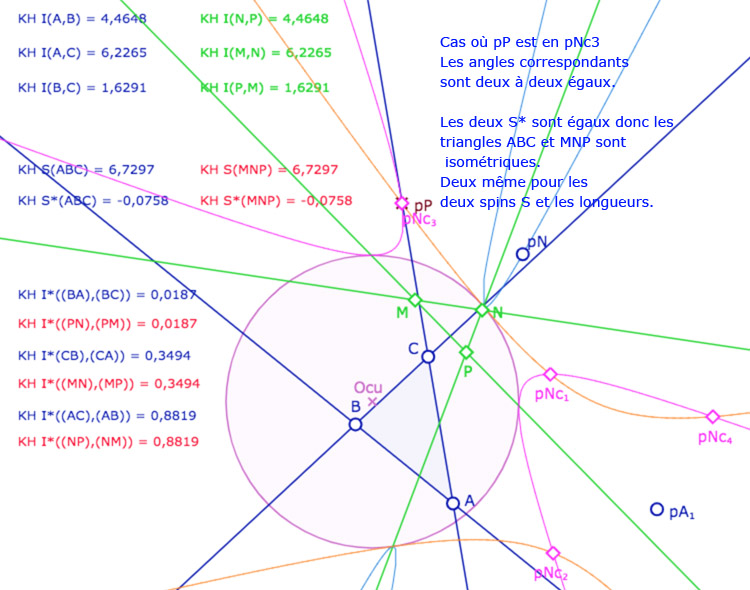
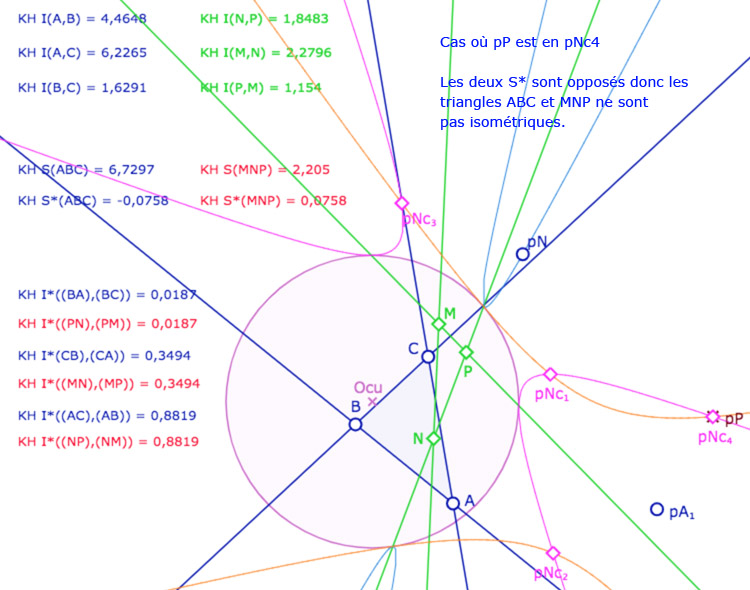
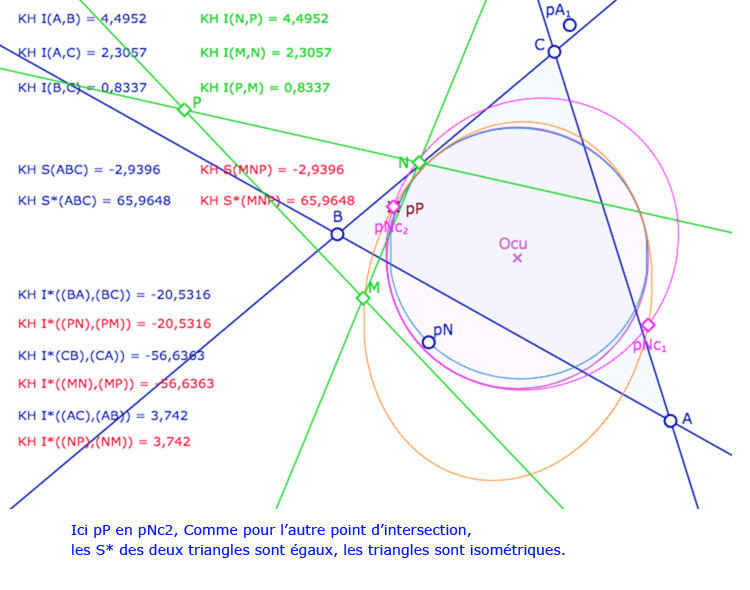
On ajoute alors un triangle \(MNP\). A ce stade de l’exposé, on devrait tracer les droites associées et non pas les segments, car les KE-segments n’ont pas encore été définis. On a choisi de tracer les segments euclidiens usuels pour éviter d’alourdir la figure. Depuis le point \(N\), on construit le KE-cercle de centre \(N\) et de rayon \(BC\). C’est la conique rose. Elle coupe la conique orange en général en 4 points \(Nc_1, Nc_2, Nc_3, Nc_4\) (soit les points \(C_i\) depuis \(N\)).
Les points \(M,N,P\) sont aimantés par plusieurs objets, mais la figure est surtout construite pour que l’on place \(M\) en \(A_1\), \(N\) sur la conique bleue et \(P\) sur l’un des 4 points \(Nc_1, Nc_2, Nc_3, Nc_4\). Dans ce cas les deux triangles \(ABC\) et \(MNP\) ont leurs côtés deux à deux égaux. L’intérêt de la figure est que certains triangles ont même spin d’autres ont un spin opposé.
Voici deux petites galeries d’illustrations de ce que l’on peut réaliser avec la figure dynamique suivante. On a ajouté le spin angulaire \(S^*\) défini un peu plus loin.
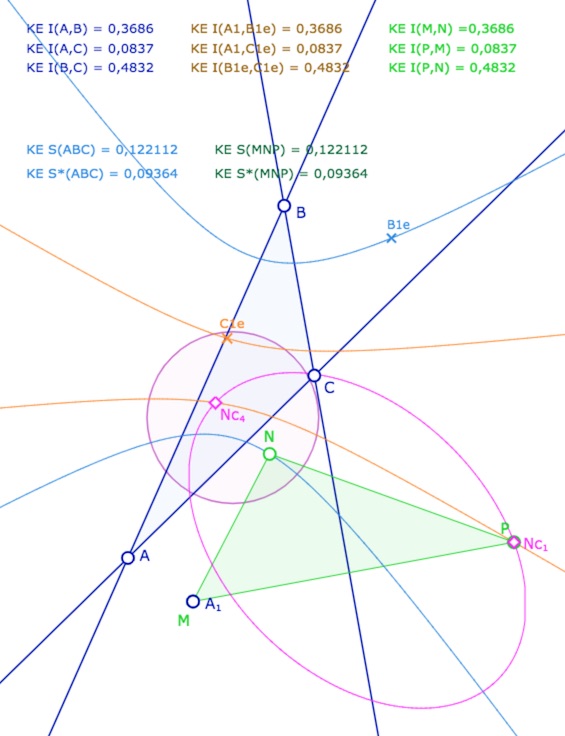
Illustration 1 : le cercle rose est représenté par une hyperbole – P sur les 4 points.
Deux cas sont avec même spin, deux cas avec des spins opposés.
Autre illustration
Illustration 2 : le cercle rose est représenté par une ellipse – P sur les 4 points.
Deux cas sont avec même spin, deux cas avec des spins opposés.
Dans certains cas, les deux coniques rose et orange n’ont que deux intersections. Dans ce cas les triangles ont même spin., sur les deux intersections.
Manipulation de la figure
Placer \(M\) sur \(A_1\), \(N\) sur la conique bleu, et \(P\) sur les 4 points \(Nc_i\).
Déplacer \(N\) sur la conique bleue, les points \(A, B, C\) et \(A_1\).
Préférer ouvrir cette figure (plus grande, et commentée) dans un nouvel onglet.
B – Dans le prolongement KH du modèle hyperbolique KB
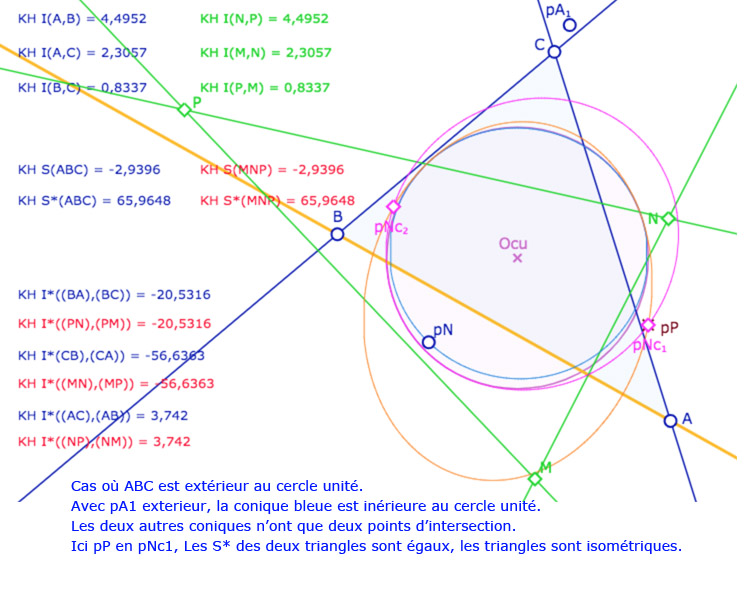
On fait exactement la même figure, avec les mêmes notations. On rappelle que les KH-cercles extérieurs au cercle unité sont toujours tangents à ce cercle (en les point de contact de la polaire du centre). Il faut être vigilant, dans KH, à ce que les points doivent être tous soit intérieurs au cercle unité, soit tous extérieurs car une isométrie ne peut échanger un point de l’intérieur au cercle unité (\(q < 0\)) avec un point extérieur (\(q > 0\)). Cette précaution prise, on a le même résultat vis à vis des invariants \(S\) et \(S^*\). Voici une galerie de ce que l’on peut explorer.
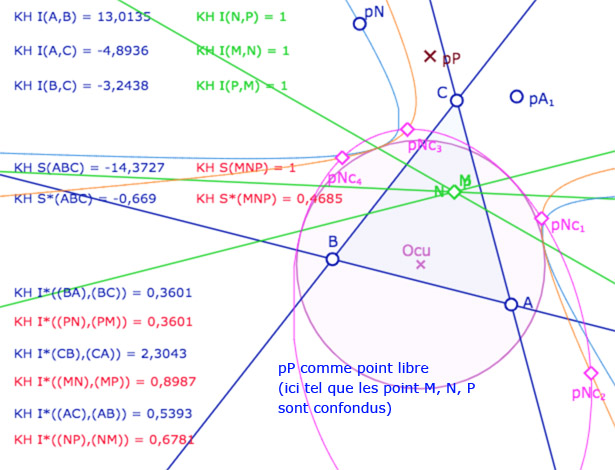
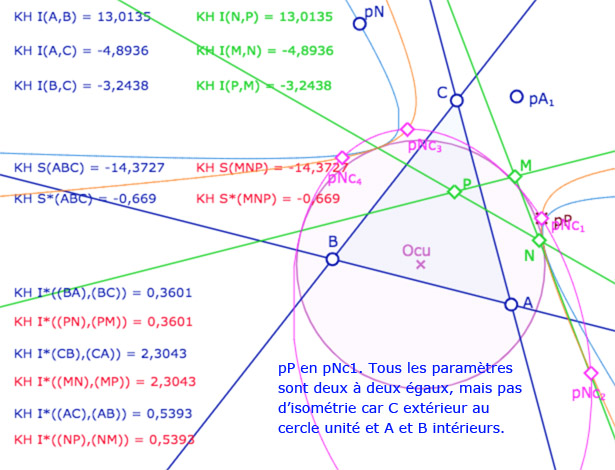
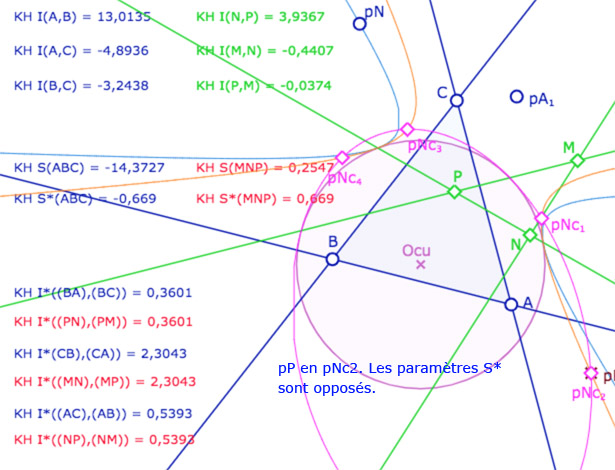
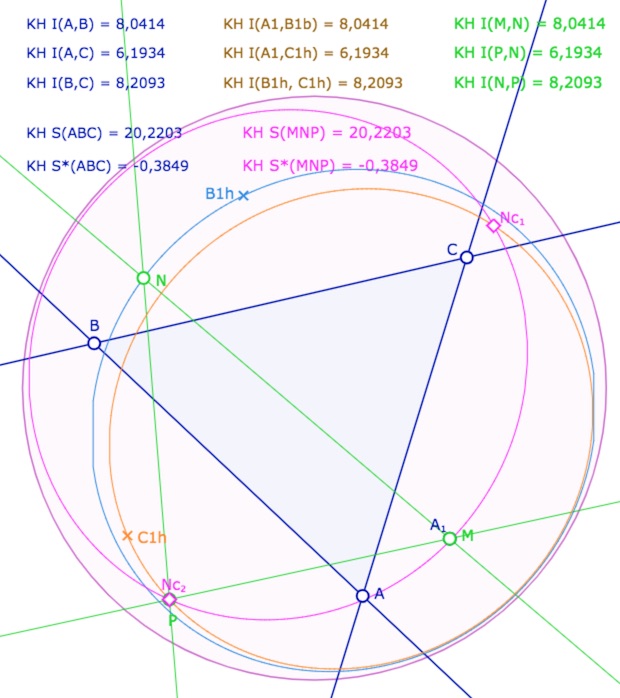
Quatre illustrations dans KH avec \(M\) en \(A_1\), \(N\) sur la conique bleue
et \(P\) sur l’un des 4 points \(Nc_1, Nc_2, Nc_3, Nc_4\).
Le cas du modèle hyperbolique KB : quand tous les points utilisés sont dans le cercle unité
Dans ce cas, les KH-cercles étant à l’intérieur du cercle, sont des nécessairement des ellipses. Elles n’ont alors – semble-t-il – que deux points d’intersection qui correspondent aux deux cas où le spin est celui du triangle initial.
Manipulation de la figure dans KH
Placer \(M\) sur \(A_1\), \(N\) sur la conique bleu, et \(P\) sur les 4 points \(Nc_i\).
Déplacer \(N\) sur la conique bleue, les points \(A, B, C\) et \(A_1\).
Préférer ouvrir cette figure (plus grande, et commentée) dans un nouvel onglet. Plus facile, par exemple, pour reproduire l’illustration précédente.
Troisième cas d’égalité des triangles – version angles
Dans l’article précédent, à la section sur les angles, on a défini l’invariant de deux droites – l’angle de deux droites – \(I^*(d_1,d_2)\) à partir de leurs pôles \(P_1\) et \(P_2\), par \(I^*(d_1,d_2)=I(P_1,P_2)\) : l’angle de deux droite est la distance entre leurs pôles. On avait d’ailleurs signalé cette remarque de Daniel Perrin :
Ce qui précède est une nouvelle illustration de la puissance de la polarité. Toute assertion concernant les longueurs aura désormais une traduction en termes d’angles et réciproquement.
Daniel Perrin – Partie 4 – page 150
On peut alors définir le spin angulaire d’un triangle \(ABC\) par le spin associé des droites du triangle \(S^* \left((AB), (BC), (CA)\right)\), \(S^*\) étant lui-même défini par dualité. On le notera simplement \(S^*(ABC)\). Dans les figures, il est construit à partir des pôles des droites du triangle.
On a alors un cas d’égalité des triangles qui n’existe pas dans le cas euclidien :
Si deux triangles ont leurs angles de droites égaux et ont même spin angulaire, alors ils sont égaux.
Voilà un point fondamentalement différent du cas euclidien où l’on sait bien que la donnée des trois angles d’un triangle ne le détermine qu’à similitude prés. De fait, en géométrie euclidienne, comme la somme des angles d’un triangle est égale à π, se donner trois angles n’est rien de plus que s’en donner deux et l’argument de dimension montre que cela ne suffit certainement pas à déterminer un triangle à isométrie près. On n’a plus cette contrainte en géométrie non euclidienne. La dissymétrie entre longueurs et angles qui apparaît ainsi en géométrie euclidienne est une nouvelle manifestation de l’absence de polarité qui tient au fait que la forme q est dégénérée.
Daniel Perrin – Partie 4 – Page 155
Illustration dynamique du théorème (version KE)
Dans les deux figures précédentes, sur l’aspect « longueurs » de ce troisième cas d’égalité, on avait ajouté le spin angulaire des deux triangles \(ABC\) et \(MNP\), et on a pu vérifier que, quand il y a « égalité des triangles », il y a égalité aussi des spins angulaires, ce qui n’est qu’un sens du théorème. On se propose ici de réaliser une figure qui illustrera pour les angles ce que l’on a fait pour les longueurs, et en particulier construire des triangles ayant les mêmes angles de droites mais dont les spins angulaires sont opposés et donc les triangles non isométriques. Cela pourrait paraître délicat à réaliser car on n’a pas (pas encore) de report d’angle. Mais comme le signale régulièrement Daniel Perrin dans son texte, son approche dispose d’un outil conceptuel extraordinairement efficace, la dualité. On va facilement pouvoir réaliser une telle figure, simplement par dualité de la version « longueur ».
Avant de détailler la méthode utilisée, voici une galerie de copies d’écran de la prochaine figure. On a choisi (par facilité car il n’y a pas de problème dans le cas elliptique) d’afficher directement les angles en degrés, au lieu de l’invariant \(I^*\) qui définit \(S^*\), soit l’angle \(\theta\) tel que \(I^*(d_1, d_2) = cos^2 \theta\), avec \(\displaystyle \theta \in \left[ 0, \frac{\pi}{2} \right]\). (On saute alors – juste pour cette figure – au chapitre 5)
Galerie de 4 illustrations (dans KE) sur le théorème dans sa version angulaire
Le principe de la construction
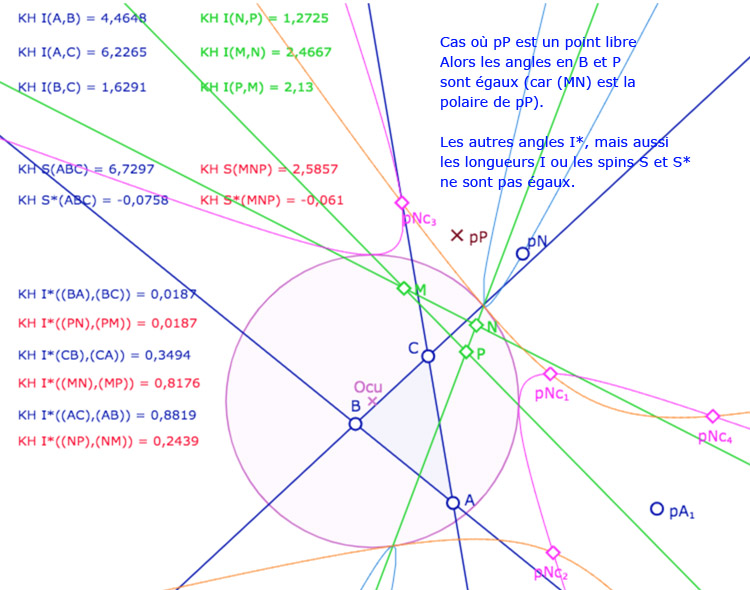
On transforme une partie de la figure précédente en macro-construction : depuis le cercle unité \(CU\), les sommets \(A, B, C\), le point \(A_1\) et le point \(N\) on renvoie les trois coniques, bleue, orange, rose, et les 4 points d’intersection \(Nc_1, Nc_2, Nc_3, Nc_4\). On applique alors cette macro à la configuration suivante :
On se donne un point \(pA_1\), et un point \(pN\) (le préfixe \(p\) – pour pôle – rappelant que l’on est dans la figure duale). On applique la macro aux pôles des droites, \(KEpoleAB, KEpoleBC, KEpoleAC\), puis \(pA_1\) et \(pN\). La macro envoie, en particulier la conique bleue (qui est le lieu auquel va être attaché \(pN\)) et les 4 points notés ci-dessous \(pNc_1, pNc_2, pNc_3, pNc_4\). On se donne enfin un point \(pP\), et on construit le triangle \(MNP\) intersection des polaires elliptiques des trois points \(pA_1\) (le point \(M\) de la figure précédente), \(pN\) et \(pP\). On aimante ensuite \(pN\) à la conique bleue, et \(pP\) aux 4 points \(pNc_1, pNc_2, pNc_3, pNc_4\).
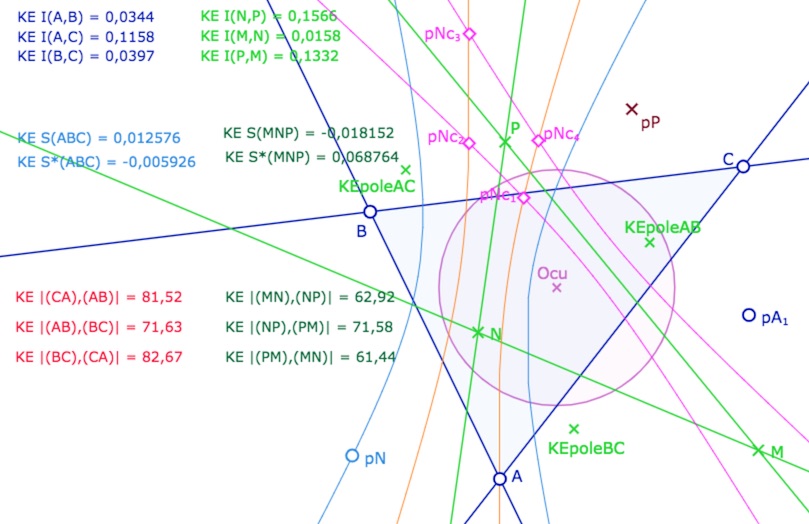
Dans cette illustration, \(pP\) n’est pas sur les points d’intersection des coniques.
Et donc les triangles \(ABC\) et \(MNP\) n’ont pas les angles égaux,
mais c’est le cas dès que \(pP\) est bien sur l’un des 4 points.
Manipulation de la figure
• Placer \(pP\) sur l’un des 4 points \(pNc_1, pNc_2, pNc_3, pNc_4\).
• Déplacer le point \(pN\) qui doit rester sur la conique bleue et le point \(pA_1\).
• Agir sur les sommets \(A, B, C\), mais aussi déplacer le centre \(O_{cu}\).
Préférer ouvrir cette figure dans un nouvel onglet (figure plus grande, sans contrainte permettant d’afficher les points de construction, les pôles et les coniques.
Illustration dynamique dans le plongement hyperbolique KH
La figure est construite de la même façon, mais KH n’est pas une géométrie hyperbolique, juste le plongement de la géométrie hyperbolique à l’intérieur du cercle unité. On se propose d’illustrer des résultats un peu plus généraux que le théorème lui-même, en particulier, si les points n’ont pas toujours même signe par rapport à la forme quadratique, et dans ce cas, il n’y a pas de mesure d’angles. Ainsi, pour les mesures, on revient à l’invariant initial \(I^*\), qui, lui, existe dans tous les cas.
On commence par illustrer le théorème lui-même, avec les six points \(A, B, C\) et \(M, N, P \) soit tous dans le cercle unité, et donc dans le cadre hyperbolique de KB, soit tous à l’extérieur – donc spécifiquement dans le plongement KH.
Sept illustration de la prochaine figure qui présentent 7 cas particuliers de la version « angulaire » du théorème
On poursuit en illustrant la même figure mais dans un contexte « hors théorème » car deux sommets de \(ABC\) sont intérieurs au cercle unité et un autre extérieur, donc il ne peux y avoir d’isométrie sur \(MNP\). Mais c’est intéressant de voir que l’on trouve encore des situations à quatre cas, deux avec le même invariant \(S^*\) pour les deux triangles, et deux avec des valeurs opposées.
Cinq illustration de la prochaine figure qui présentent 5 cas hors du contexte du théorème.
Manipulation de la figure
• Placer \(pP\) sur l’un des 4 points \(pNc_1, pNc_2, pNc_3, pNc_4\).
• Déplacer le point \(pN\) qui doit rester sur la conique bleue et le point \(pA_1\).
• Agir sur les sommets \(A, B, C\), mais aussi déplacer le centre du cercle unité \(O_{cu}\).
Préférer ouvrir cette figure dans un nouvel onglet pour une manipulation plus générale.
Dans les deux cas – iframe dans le site directement ou en ligne – on peut toujours revenir à la configuration initiale en rechargeant soit l’iframe soit la page DGPad.
Formules d’Al-Kashi
et applications
Pour les deux premiers « cas d’égalité des triangles », qui mélangent longueurs et angles, il faut une formule reliant les deux, du type « formule d’Al-Kashi ». Daniel Perrin obtient ainsi (p. 157)
Soient \(A, B, C\) trois points distincts et non isotropes. En notant \(a, b, c\) les droites \((BC), (AC), (AB)\) respectivement, alors :
\(I(B,C) = \left(1-I(A,B)\right)\left(1-I(A,C)\right)I^*(b,c)-I(A,B)I(A,C)+2S(A,B,C)\)
Corollaires
Si le point \(A\) est différent de \(B\) et de \(C\) et si les droites \(b\) et \(c\) ne sont pas isotropes, alors :
\(I^*(b, c) = \displaystyle \frac{I(B,C)+I(A,B)I(A,C)-2S(A,B,C)}{ \left(1-I(A,B)\right)\left(1-I(A,C)\right)}\)
Ainsi, dans un triangle \(ABC\), l’angle de droites \(I^*(b, c)\) se calcule à partir des longueurs et du spin des trois sommets.
On a la version duale du corollaire précédent
\(I(B, C) = \displaystyle \frac{I^*(b,c)+I^*(a,b)I^*(a,c)-2S^*(a,b,c)}{ \left(1-I^*(a,b)\right)\left(1-I^*(a,c)\right)}\)
Premier cas d’égalité des triangles
On considère deux triplets de points non isotropes et non alignés. Alors deux triangles ayant des côtés égaux, formant en le sommet commun des angles de droites égaux, et ayant même spin, sont égaux.
Avec la contrainte pour KH, sur la position des points par rapport au cercle unité, comme dans le cas précédent du troisième cas d’égalité.
Illustration dans KE et figure dynamique
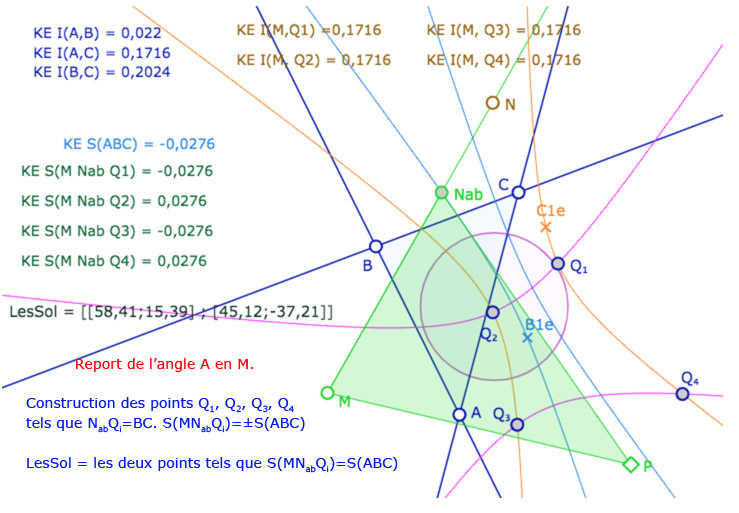
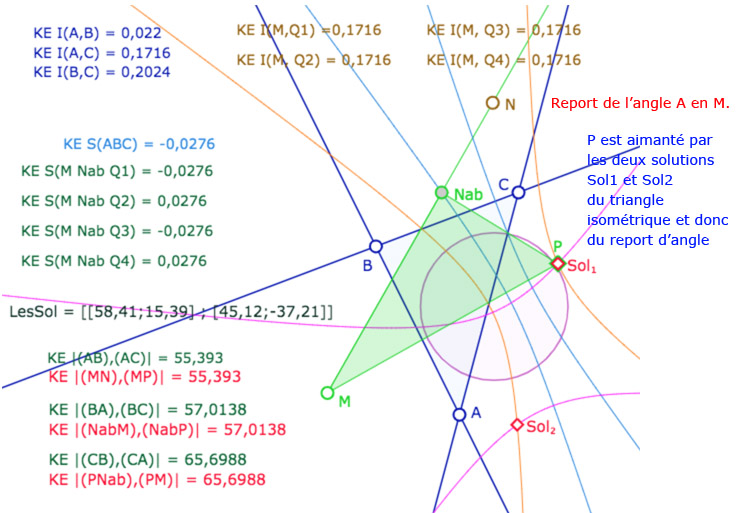
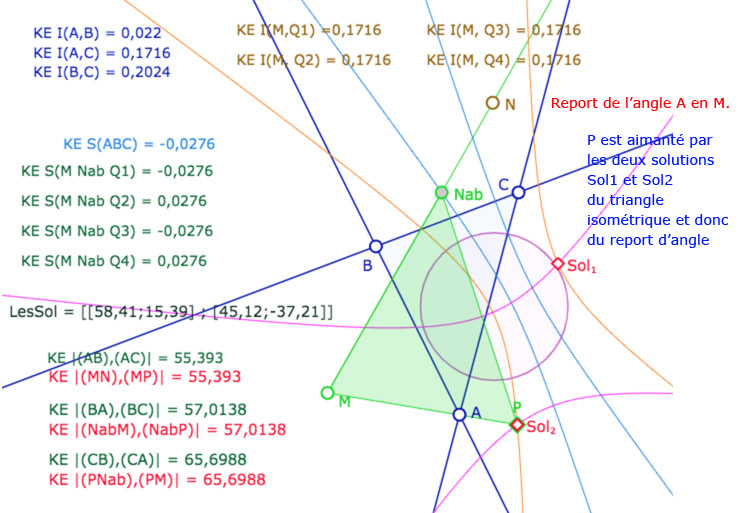
En pratique faire un outil de report d’angle ou illustrer le premier cas d’égalité des triangles revient à faire la même figure. Voici une première illustration. Dans un premier temps on se propose de reporter en un point \(M\) depuis une droite \((MN)\) – l’angle de droite en \(A\) du triangle \(ABC\). On commence par construire \(N_{ab}\) une des intersections de \((MN)\) avec le cercle de centre \(M\) de rayon \(AB\) – soit la conique bleue – et de ce point, comme dans les figures précédentes, les 4 intersections de cercles \(Q_1, Q_2, Q_3, Q_4\) qui réalisent \(N_{ab}Q_i=BC\). On a calculé les longueurs concernées, ainsi que les spins des triangles : deux points conviennent, deux autres non. Comme les intersections des coniques ne sont pas continue en manipulation directe, on utilise un petit programme JavaScript pour déterminer, dans la liste \(LesSol\), ceux des deux points solutions, que l’on nomme \(Sol_1\) et \(Sol_2\). Un point \(P\) est aimanté par ces deux points. En même temps que le report d’angle, on illustre le théorème précédent sur les triangles \(ABC\) et \(MN_{ab}P\).
Galerie de 5 copies d’écran de la figure suivante – dans le modèle elliptique KE
Ouvrir la figure associée dans un nouvel onglet
On voit que cette figure est, de fait, construite à partir du troisième cas d’égalité des triangles, ce serait de même pour le deuxième cas d’égalité.
Deuxième cas d’égalité des triangles
Soient trois droites \(a, b, c\) non isotropes et non concourantes. On note \(A, B, C\) les intersections des droites \(b, c\), \(a, c\) et \(a, b\) respectivement. Alors si deux triangles ayant
• Les mêmes angles en \(B\) et \(C\),
• La même longueur \(I(B,C)\), et
• Le même spin angulaire \(S^*(a, b, c)\)
sont égaux.
La contrainte pour KH porte sur l’invariant \(I^*\) des angles, ce qui se traduit par le fait que les pôles des trois droites doivent être tous trois soit à l’intérieur, soit à l’extérieur du cercle unité.
Autres conséquences
de la formule d’Al-Kashi
Alignement de trois points (p. 158)
Soient \(A, B, C\) trois points non isotropes. Alors \(A, B, C\) sont alignés si et seulement si \(2S(A, B, C)=I(A,B)+I(B,C)+I(C,A)-1\).
En particulier si les trois points sont alignés, on a alors
\(4I(A,B)I(B,C)I(C,A)=\left(I(A,B)+I(B,C)+I(C,A)-1 \right)^2\)
Cas particulier où deux points des trois points sont orthogonaux
Si les trois points \(A, B, C\) sont alignés et non isotropes, et si \(B, C\) sont orthogonaux, alors \(I(A, B)+I(B, C)=1\).
Manipulation d’une figure associée à ces propriétés

Utiliser les indications précédentes, (précisées dans la figure en ligne suivante).
Préférer ouvrir la figure dans un nouvel onglet.
Conséquence pour l’invariant de « couples mixtes »
Juste avant d’introduire le spin de trois points ou de trois droites, Daniel Perrin avait défini l’invariant d’un coupe « point-droite » (p. 151) de la façon suivante :
Soit \(A\) un point et \(d\) une droite, tous les deux non isotropes.
Alors on défini \(I(A,d) = I(A,D)\) où \(D\) est le pôle de \(d\).
La quantité \(I(A,d)\) joue le rôle de distance d’un point à une droite. D’après ce qui précède, en notant \(N\) le projeté orthogonal de \(A\) sur \(d\), c’est-à-dire l’intersection des droites \(d\) et \((AD)\), alors, si \(N\) n’est pas un point isotrope, on a \(I(A,d) + I(A,N) = 1\).
Illustrations
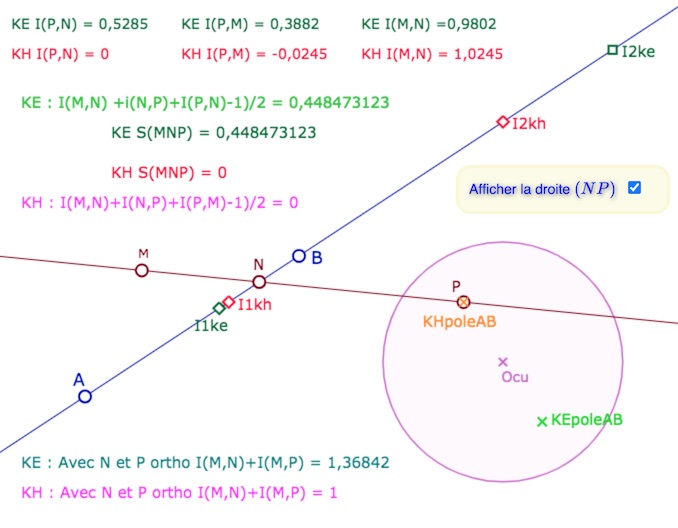
On peut revenir sur la figure précédente pour illustrer cette dernière relation, en plaçant \(P\) sur un des pôles (KE ou KH) de la droite \((AB)\), \(N\) sur \((AB)\) et \(M\) sur la droite \((NP)\). Alors, \(N\) est le projeté orthogonal de \(M\) sur \((AB)\). On illustre, dans les deux cas, (outre \(I(P,N) = 0\)) l’égalité \(I(M,N)+I(M,P) =1\) :
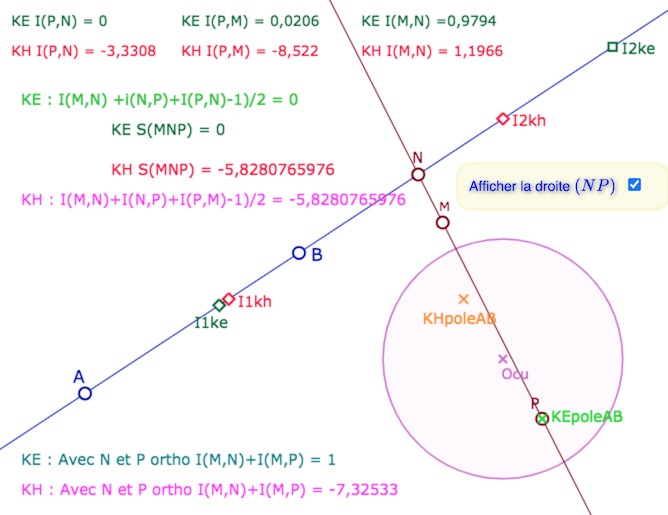
Projection orthogonale \(N\) du point \(M\) sur la droite \((AB)\)
Ci dessus dans KE, ci-dessous dans KH.
Les triangles isocèles
Le chapitre 4 se termine par une étude détaillée des triangles isocèles, avec deux approches, dont une basée sur cette relation qui découle des corollaires de la formule d’Al-Kashi : avec les notations précédentes, on a
\(\left(1-I(A,B)\right) \left(1-I(B,C)\right) \left(1-I(C,A)\right) \left(I^*(a,b)-I^*(a,c)\right) =\)
\(\left(I(A,B)-I(A,C)\right) \left(1+2S(A,B,C)-I(A,B)-I(B,C)-I(C,A)\right)\)
En conséquence, pour trois points \(A, B, C\) non isotropes, non alignés, et tels que les droites \(a=(BC), b=(AC), c=(AB)\) ne soient pas tangentes au cercle unité, on a la propriété suivante :
Si de plus \(A\) n’est orthogonal ni à \(B\) ni à \(C\), et si \(B\) et \(C\) on même signe par rapport à la forme quadratique – ie, pour KH uniquement, tous les deux sont intérieurs ou extérieurs au cercle unité – alors il y a équivalence entre \(I(A,B)=I(A,C)\) (longueurs égales) et \(I^*(a,b)=I^*(a,c)\) (angles égaux en \(B\) et \(C\)).
Dans ce cas on dit que le triangle \(ABC\) est isocèle en \(A\).
Bien entendu – et c’est l’autre définition – dans ce cas une symétrie orthogonale passant par \(A\) échange les points \(B\) et \(C\).
Propriétés des triangles isocèles
La hauteur du triangle issue de \(A\) est aussi médiatrice, médiane et bissectrice du triangle. La médiane et la bissectrice issue de \(A\) qui ne sont pas égale à la hauteur coïncident.
Réciproquement, si dans un triangle une médiatrice est aussi médiane (ou hauteur ou bissectrice) alors le triangle est isocèle.
Par contre, l’autre médiatrice de \(B\) et \(C\) n’est pas une droite remarquable du triangle : elle ne passe pas par le sommet \(A\).
Manipulation d’une figure dans KE et KH
Dans cette figure, les angles sont représentés par les invariants \(I^*\).
On a ajouté les deux autres médiatrices (vert clair et orange), passant par les points \(J\) qui ne sont pas « droites remarquables du triangle ».
Agir sur \(M\) pour modifier la symétrie orthogonale du triangle, mais aussi sur \(A\) et \(B\).
On peut aussi déplacer le cercle unité par son centre.
Préférer ouvrir cette figure dans un nouvel onglet.
Liste des autres articles sur ces modèles
Les modèles projectifs KE et KH – 1 – les droites | KE KH – 2a – Cercles
KE KH – 2b – les « cercles-paraboles » | KEKH – 3 – Longueurs – distances – angles