Dans la conjugaison avec le disque de Beltrami, que ce soit dans le menu PS ou dans les anciens articles sur la PS (Malfatti ou pentagone orthogonal) et même plus récemment dans l’article sur l’utilisation des macros de KB par conjugaison, nous avons toujours utilisé la projection originale de Beltrami. On va vu que celle-ci, en envoyant son origine sur la surface – le point \(X\) du repère 3D – en l’origine de son cercle-limite, place de fait l’horicycle image de la pseudosphère à la droite de l’origine du cercle, avec cette conséquence que les autres feuilles que la feuille principale, même les deux adjacentes, sont peu visibles dans cette correspondance.
Quelques figures un peu lourdes (de la section « points multifeuilles ») peuvent ralentir l’arrivée des premières figures de l’article. Attendre un peu, si nécessaire, les relancer avec l’icone appropriée de l’iframe.
Introduction
En voyant cette illustration de la projection de la pseudosphère sur le plan avec un angle très faible entre les bornes de la feuille principale, et en lisant ces deux lignes, on comprend vite qu’il est possible d’adapter cette projection.
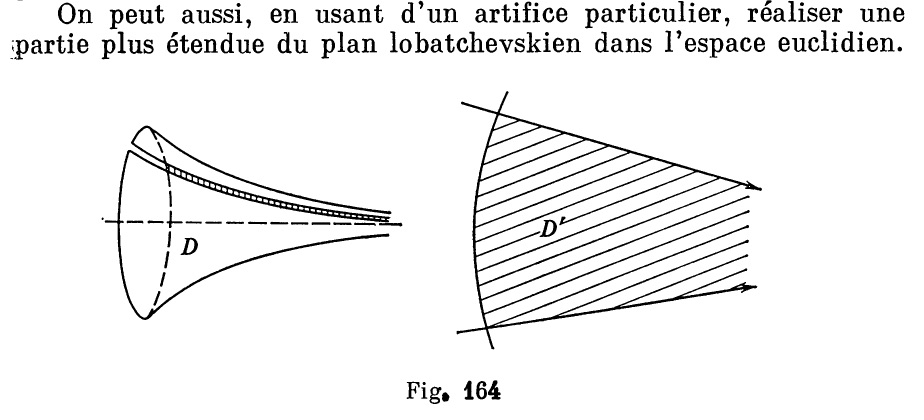
« Géométrie Supérieure » – Nicolai Efimov (Ed. MIR – 1981) – page 557
Un moyen de le faire, implicitement suggéré par cette illustration, est de déplacer l’origine de la projection de Beltrami, toujours sur l’axe des abscisses, mais à gauche du centre du cercle. On trouve alors cette généralisation à la projection de Beltrami (il y a 1 à la place \(k\) dans la version originale) :
\(x = \displaystyle \frac{\theta^2+ch^2(u)-k^2}{\theta^2+ch^2(u)+k^2} \quad\) et \(\quad y = \displaystyle \frac{-2\theta k}{\theta^2+ch^2(u)+k^2}\)
L’image de l’origine du repère de Beltrami sur la pseudosphère dans le disque de Beltrami est alors le point \(A\) d’abscisse \(x_A = \displaystyle \frac{1-k^2}{1+k^2}\).
Dans le contexte de la géométrie dynamique, on fait naturellement l’inverse : on se donne une nouvelle image de l’origine, ci dessous le point \(O_{ex}\) (pour « extension de l’origine »), manipulable, on en déduit la valeur de \(k^2\) ce qui permet d’appliquer la transformation précédente.
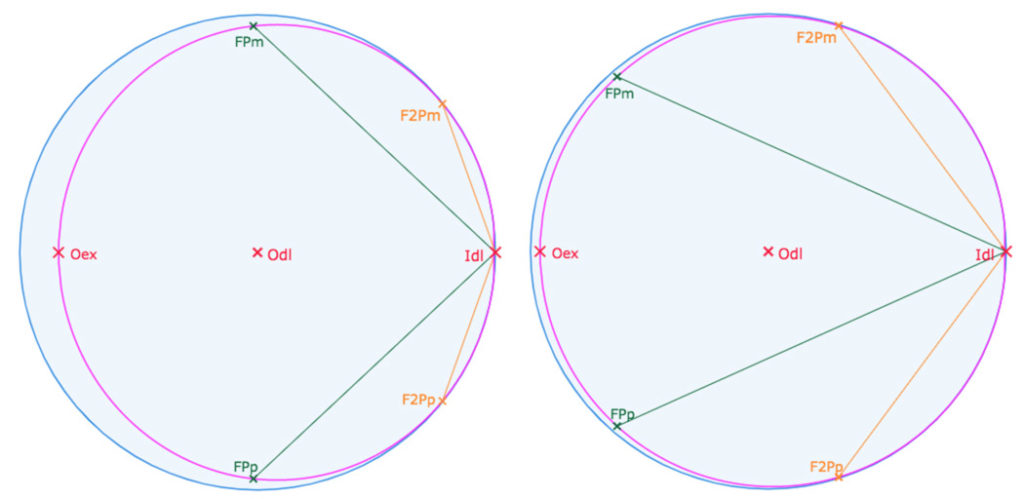
\(FP_m\) et \(FP_p\) sont les limites de la feuille principale, \(F2P_m\) et
\(F2P_p\) celles des feuilles adjacentes autour de la feuille principale.
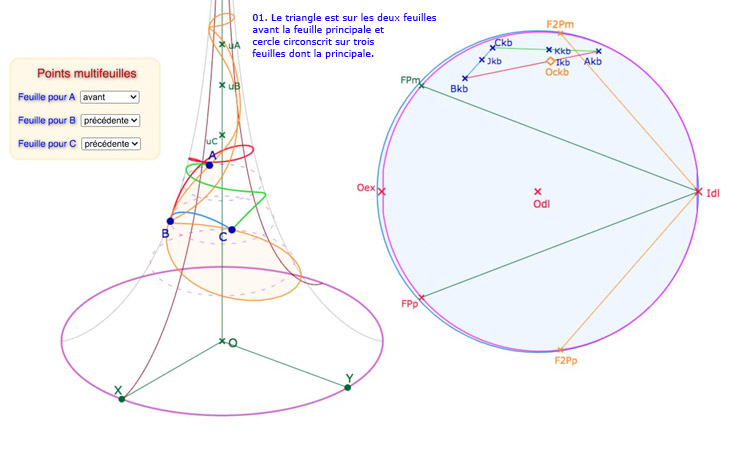
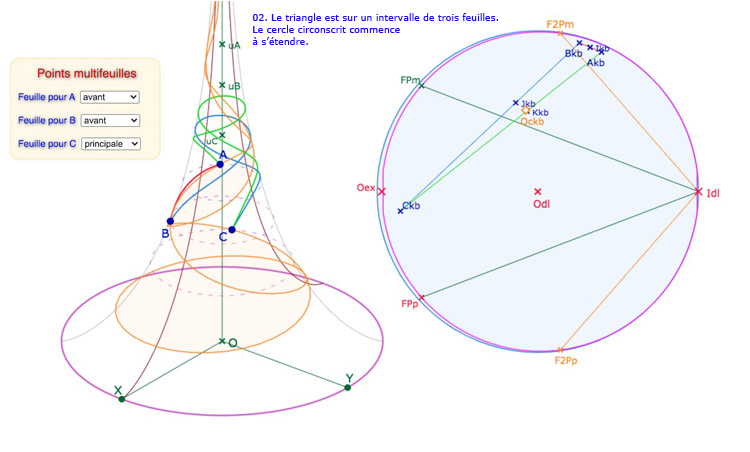
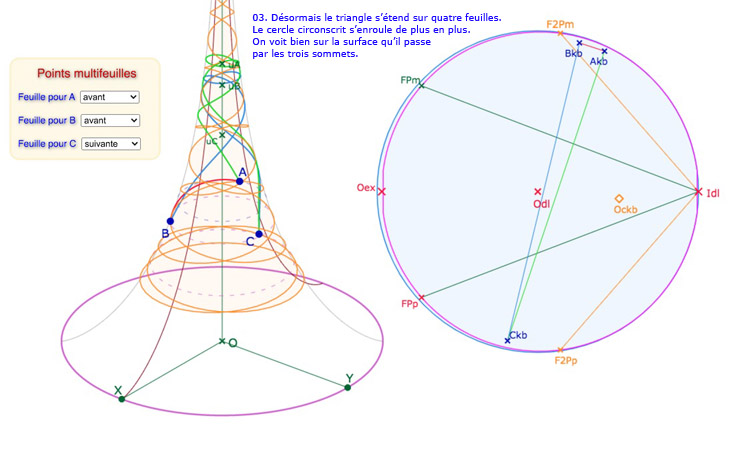
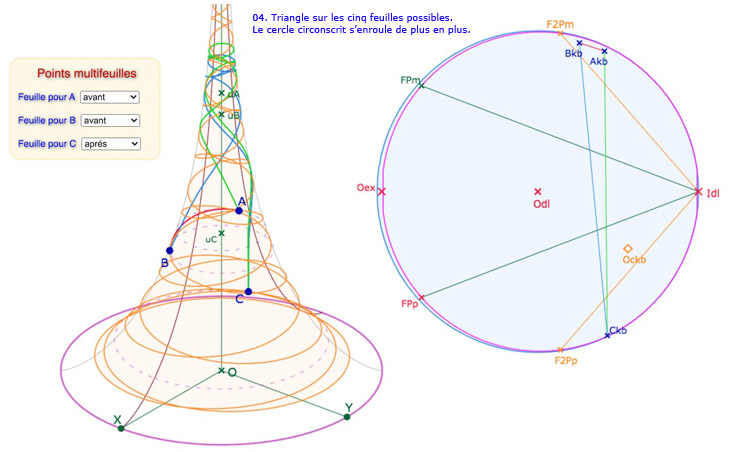
Il ne faut être illusionné sur la taille de l’horicycle limite de la pseudosphère : on n’agrandit bien entendu pas du tout la place de la PS dans la représentation du plan hyperbolique (la traduction du texte de Efimov est d’ailleurs assez ambigüe sur ce sujet). En pratique, on étend seulement la feuille principale avec comme conséquence de déployer aussi les autres feuilles. Voici l’image \(A_{kb}, B_{kb}, C_{kb}\) d’un triangle \(ABC\) sur la pseudosphère.

Passage de la version originale de Beltrami à l’extension des feuilles adjacentes.
Les droites ne restent pas parallèles à elles-mêmes comme pourrait le suggérer cette illustration.
Macro « Feuille principale adjacentes »
On a déjà développé une macro « Droite de la feuille principale » dans l’article sur les macros de la PS par conjugaison. Comme elle est conçue, on peut l’appliquer soit à la feuille principale soit au trois feuilles, la principale et les deux adjacentes. Voici un exemple de base avec la macro appliquée aux feuilles adjacentes.
• Dans un premier temps, déplacer le point \(O_{ex}\) et apprécier cette vision dynamique, assez extraordinaire, de ce qu’est un isomorphisme. Les trois droites sur la pseudosphère, construites depuis KB, sont bien entendu stables – elles auraient pu être construites de manière intrinsèque – alors qu’elles sont construites depuis les trois points \(A_{kb}, B_{kb}, C_{kb}\) eux-mêmes dépendant de \(O_{ex}\).
• Ensuite, on peut jouer sur les paramètres des différents points de la pseudosphère pour tester les droites sur plus d’une feuille. En pratique, le fait d’avoir choisi les droites potentiellement sur trois feuilles, cela permet de voir surtout les droites de l’équateur à l’équateur même si elles sont juste sur un peu plus d’un tour.
Préférer ouvrir cette figure dans un nouvel onglet, sans aucune contrainte, en particulier avec toutes les macros disponibles.
Utiliser la figure précédente (hors iframe) pour construire des figures … pour les lecteurs habitués à cette pratique.
En particulier, si vous avez déjà utilisé les macros de conjugaison sur la PS, la structure proposée ici est exactement la même. On se reportera à cet article pour revoir l’utilisation de ces macros. Deux précisions :
• à propos de l’application de la macro KBdroites 6, vous aurez remarqué les deux points \(Mf_1\) et \(Mf_2\). On utilise le premier pour construire les droites sur la feuille principale, le second sur cette feuille et ses deux adjacentes.
• à propos des macros de transfert : il n’y a plus besoin de montrer les trois points \(O_{dl}, I_{dl}, J_{dl}\) car on a choisi ici d’avoir un cercle de Beltrami unité. Il suffit de montrer seulement \(O_{dl}\). Bien entendu il faut montrer – en premier dans toutes les macros de transfert vers la PS – la constante associée à l’extension, nommée dans la figure \(k^2_{AB}\).
On peut faire les figures que l’on souhaite, et explorer le déploiement des feuilles adjacentes.
Mais, bien entendu, pour les personnes non concernées par cette utilisation assez technique, l’article se poursuit de manière classique.
Exemple de base :
le cycle circonscrit à un triangle
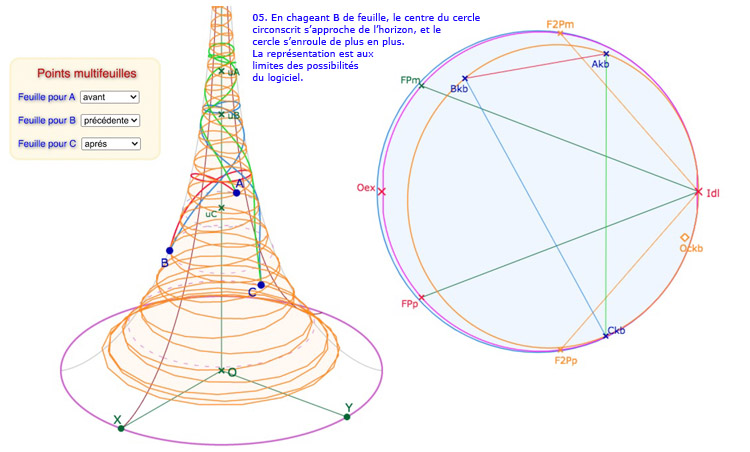
On commence par profiter de ce déploiement des feuilles adjacentes pour explorer une situation usuelle qui devient un peu plus visible. Ce sera l’occasion de fixer des données pour des constructions plus élaborées. Commençons par un cercle circonscrit dont le centre est sur la feuille suivant la feuille principale.
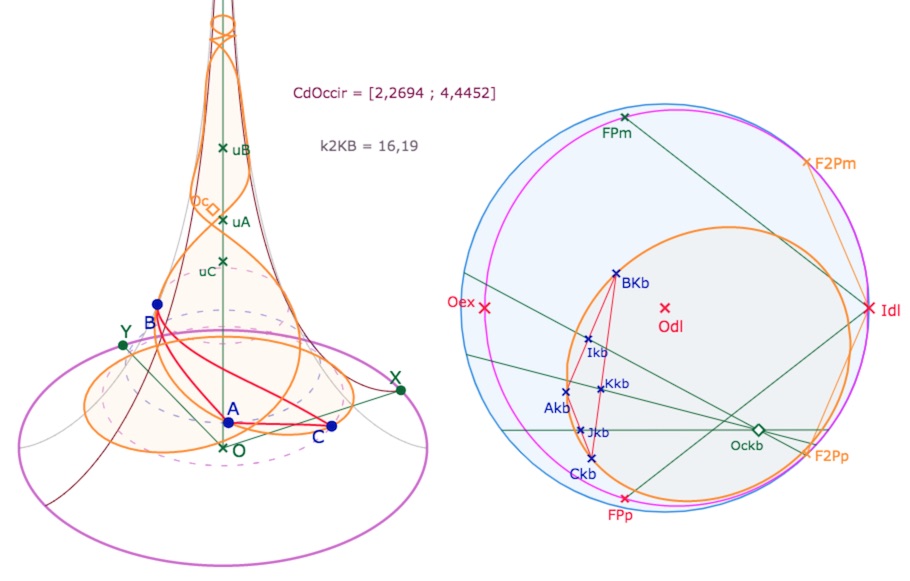
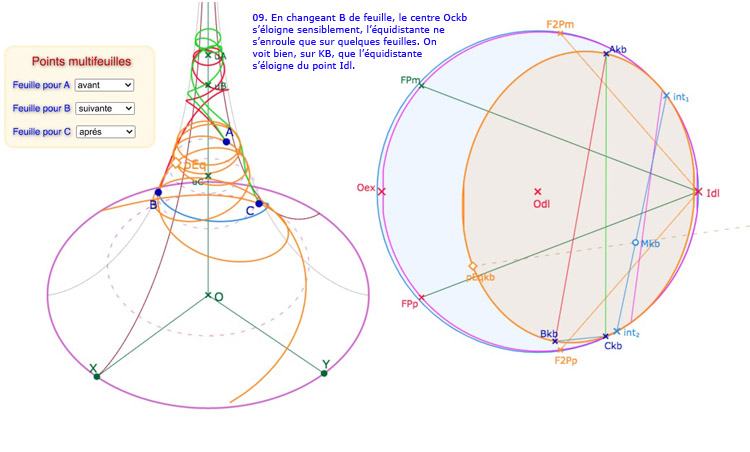
Le centre \(Oc_{kb}\) du KB-cercle circonscrit n’est pas sur la feuille principale, et le cercle circonscrit s’étend sur 4 feuilles. On a choisi ici de ne pas construire les médiatrices pour alléger la figure.
Lancer cette première figure de base dans un nouvel onglet. Pour une ouverture rapide cette figure n’implémente que le cas du cercle circonscrit entièrement sur la pseudosphère.
Cercle circonscrit partiel
Il suffit de déplacer déplacer un des sommets du triangle sur son horicycle pour que le cercle circonscrit, dans KB, rencontre l’horicycle de la pseudosphère et donc ne soit qu’en partie sur la surface.
Pour rendre compte de nombreux cas possibles dans une seule figure, on a modifié (pour la figure suivante) la KB-macro « perpendiculaire » qui renvoie une droite euclidienne entière. Dans ce cas, les médiatrices d’un KB-triangle sont toujours concourantes dans le plan euclidien. C’est le sens de ce point qui change selon que cette intersection est à l’intérieur ou non du cercle horizon. En effet, comme l’avait déjà calculé Beltrami dans son « Essai d’interprétation … », ou comme le présente Daniel Perrin dans son exploration des modèles KE et KH (présentation et page sur les cycles), si les médiatrices se coupent en dehors du cercle horizon, c’est toujours le centre du cercle circonscrit mais au sens du plongement projectif de KB dans KH, et, pour KB, ce point est le pôle de la perpendiculaire commune aux trois médiatrices : on a ainsi dans la même construction le cycle circonscrit que ce soit un cercle ou une équidistante (ou un horicycle mais pas accessible – exactement s’entend – à la manipulation directe).
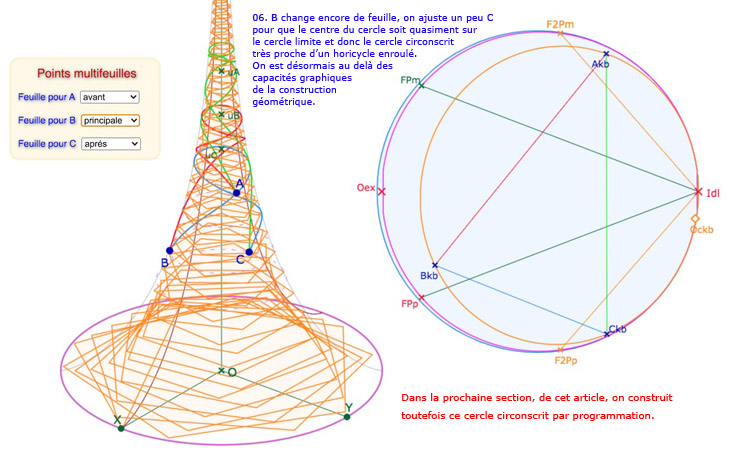
La figure se présente désormais comme ci-dessous. On a laissé les médiatrices (en pointillé) dans cette première illustration. On a choisi une configuration où le cercle circonscrit est très proche d’un horicycle, le centre du cercle étant quasiment sur le cercle-limite de Beltrami.
Dans cette configuration, le cercle circonscrit – dans KB – coupe l’horicycle de la pseudosphère en deux points, ici \(int_2\) et \(ex_2\). La construction de la partie du cercle circonscrit effectivement sur la pseudosphère se réalise assez classiquement (présentée dans cet article sur les macros de conjugaison), depuis un point \(M_{cc}\) du segment \([int_2 ex_2]\), la demi-droite \([Oc_{kb} M_{cc})\) coupe le cercle en \(Pcc_{kb}\) renvoyé sur la pseudosphère en \(P_{cc}\). Point dont on fait ensuite le lieu (par la macro PS et Transfert 6)
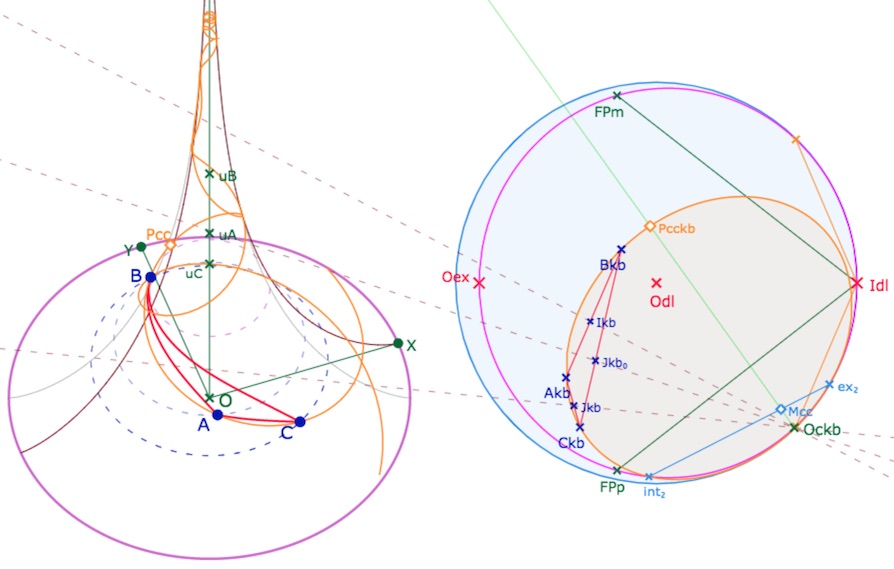
Cercle circonscrit au triangle, de l’équateur à l’équateur, en faisant de nombreux tours sur la surface
Lancer la figure dans cette configuration. On peut agir à la marge sur les points car le segment \([int_2 ex_2]\) est assez volatil : en particulier, il faut qu’il reste sous le point \(I_{dl}\). Cette figure contient, en partie, la suivante, mais ce même segment \([int_2 ex_2]\) peut alors être perturbant. Une autre version de la figure est proposée plus loin.
Équidistante
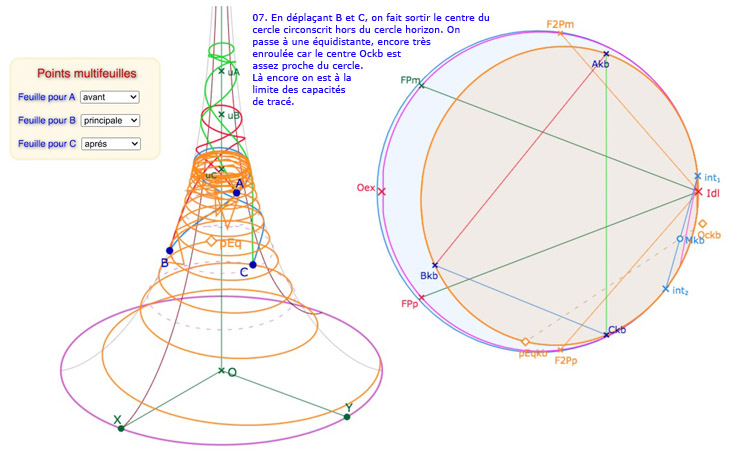
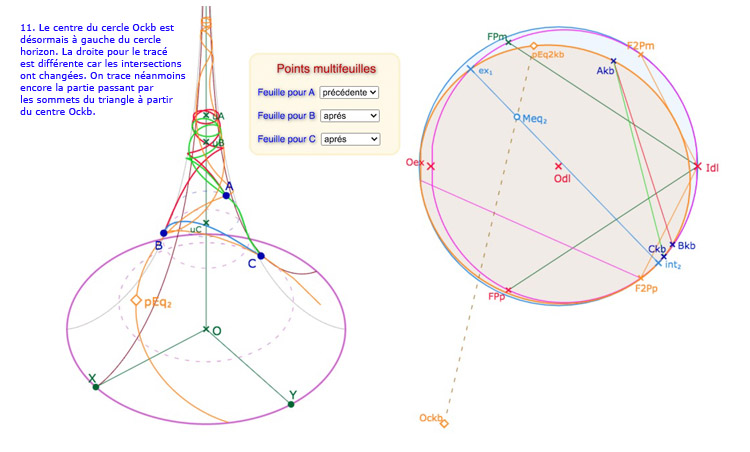
En manipulant les sommets du triangle, de quelques pixels seulement – sur leurs horicycles ou par leurs latitudes – rapidement le centre \(Oc_{kb}\) sort du cercle-limite, et donc devient le pôle de la perpendiculaire commune (la droite rose ci-dessous dans KB que l’on n’a pas renvoyé sur la PS). Le cycle circonscrit devient alors une équidistante. La construction est identique (ci-dessous partant du point à l’infini \(I_{dl}\). La seule différence est qu’on a choisi de limiter l’équidistante de l’équateur (le point \(ex_2\) dans KB) jusqu’à la limite de la feuille avant la feuille principale (le point \(ex_1\) sur le méridien \([FP_m I_{dl}]\)).
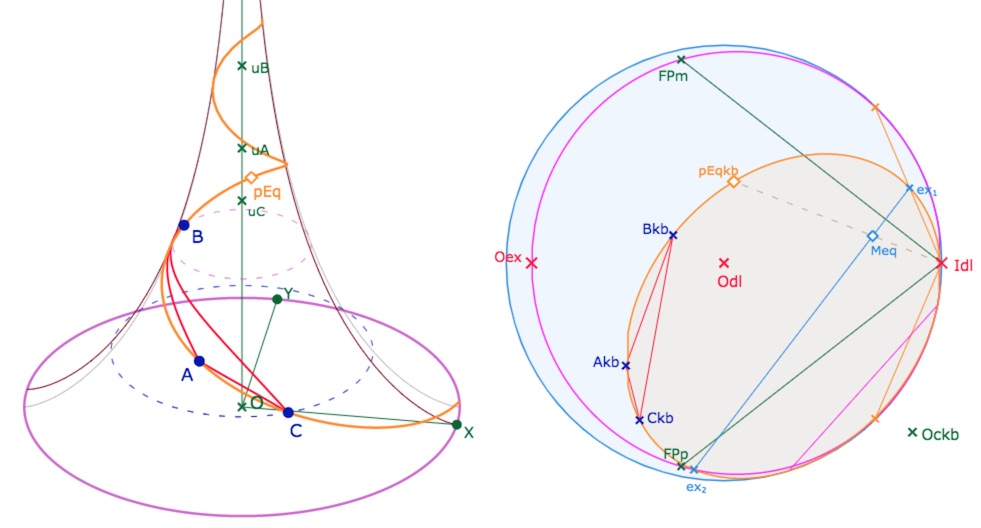
Autre partie de l’équidistante
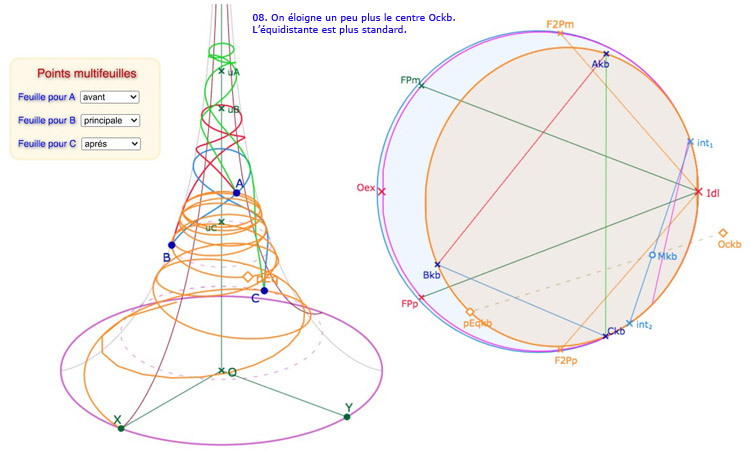
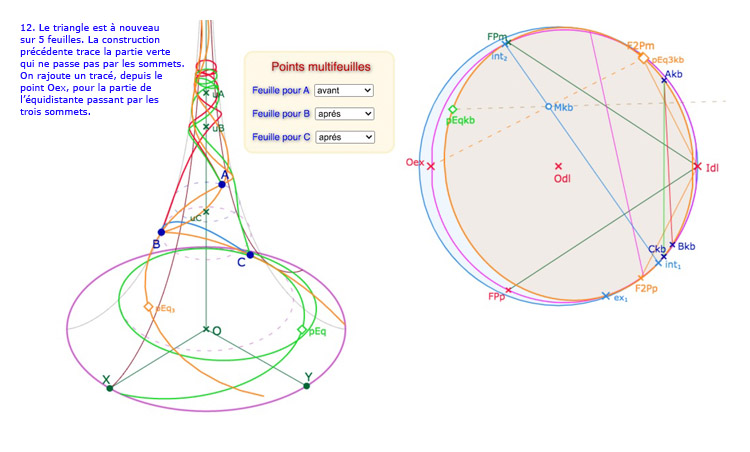
On voit bien que, dans cette configuration, les deux coniques se coupent en deux autres points, dont un au delà de la feuille adjacente. Ce sont les points \(int_1\) et \(int_2\). Il existe donc une autre partie de l’équidistante circonscrite au triangle \(ABC\), sur la pseudosphère qui est disjointe de la première (car séparée par une partie hors de la surface). L’intérêt de cette construction dépend de ce que l’on appelle « équidistante ». Soit c’est l’objet mathématique, représenté dans le modèle par une conique, et la construction suivante a du sens. Soit c’est la partie « du même côté de l’axe de la perpendiculaire commune que le triangle », dans ce cas, on se limite à la construction précédente.
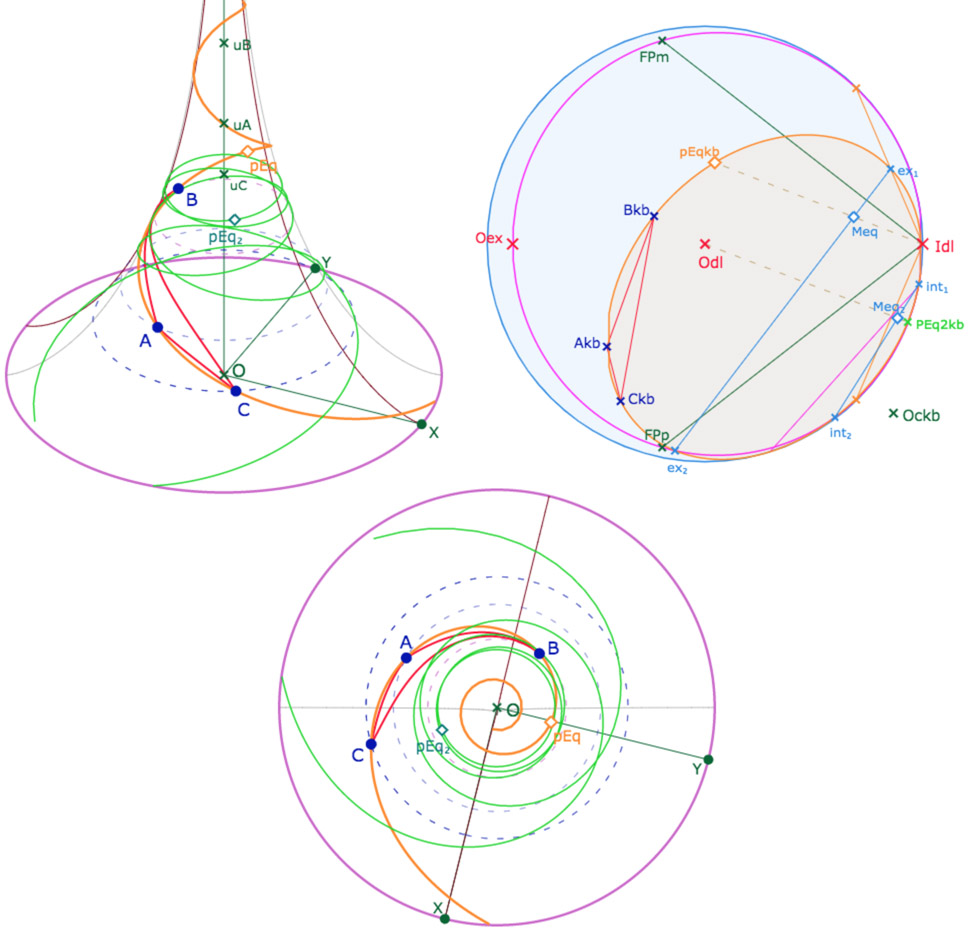
La seconde partie de l’équidistante – en vert, lieu du point \(pEq_2\) – va de l’équateur à l’équateur.
Lancer la figure dans cette configuration. Cette figure reste une figure de travail, au sens où tous les échanges d’intersections des coniques ne sont pas travaillés, mais elle est intéressante à manipuler. Éventuellement, densifier le lieu vert. Par exemple – avec une densité réglée au maximum – quand le segment \([int_1 int_2]\) se rapproche d’un méridien, et donc \(int_1\) proche de \(I_{dl}\), soit en restant en dessous, on obtient ceci :
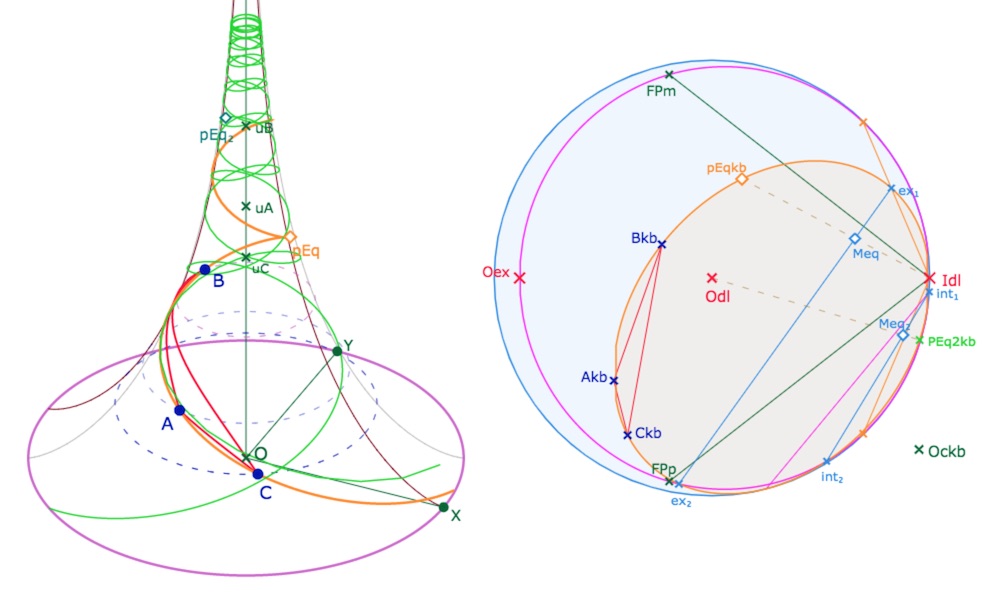
… soit même quand ce segment franchi le point critique \(I_{dl}\), avec une extrémité un peu au dessus comme ici. La figure est finalement assez stable.
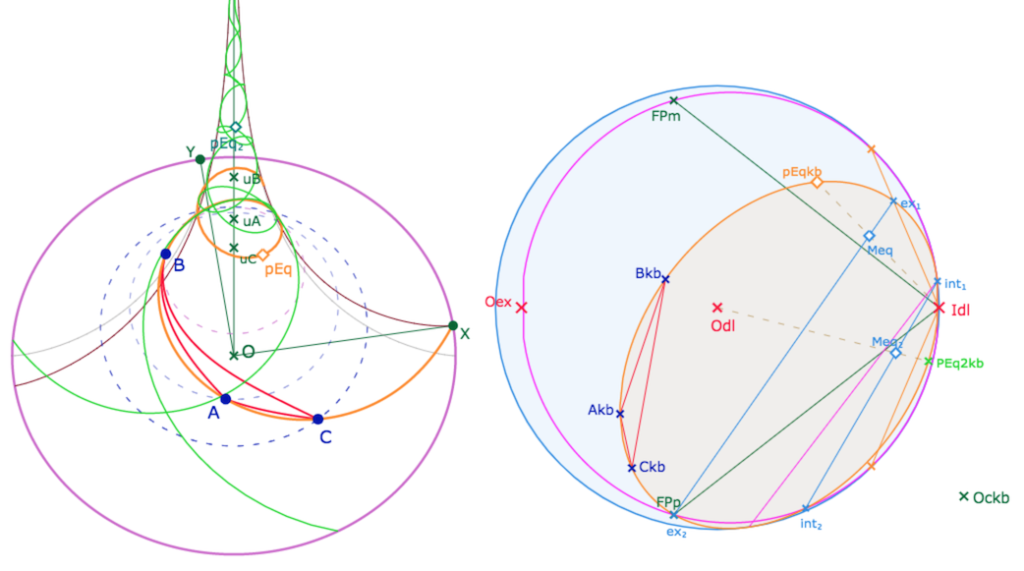
Bien-sûr, dans cette configuration, comme l’équidistante passe près de \(I_{dl}\) dans KB,
elle monte très haut (illustration coupée) sur la pseudosphère avant de redescendre.
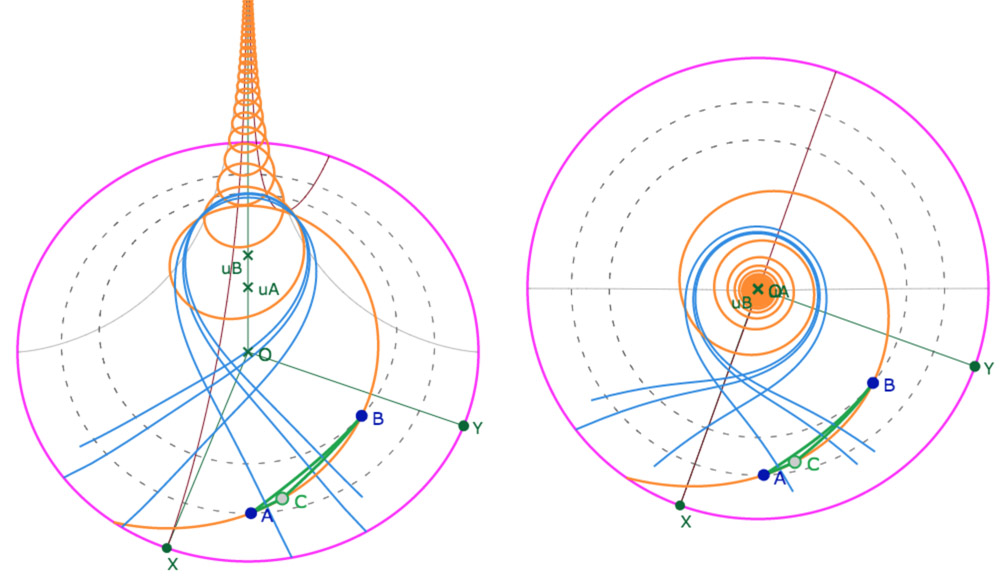
Pour rappel, le cas où la perpendiculaire commune aux médiatrices est un méridien a déjà été abordé en détail dans cette page, à la section que nous avons appelé « le rêve de Coxeter », avec un magnifique enroulement de l’équidistante, dont voici – pour le plaisir – à nouveau une illustration :
Figures avec des points multifeuilles
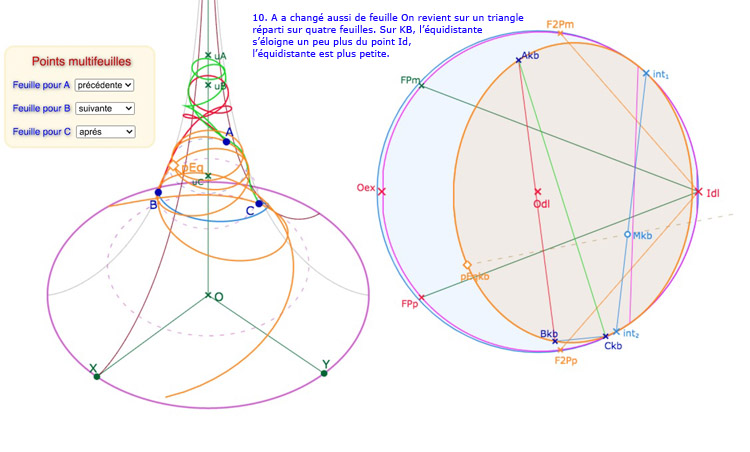
Avec ce décalage de l’origine, on voit bien mieux les deux feuilles autour de la feuille principale. On peut donc placer les points de base du triangle sur ces 5 feuilles et explorer quelques figures standards dans ce contexte.
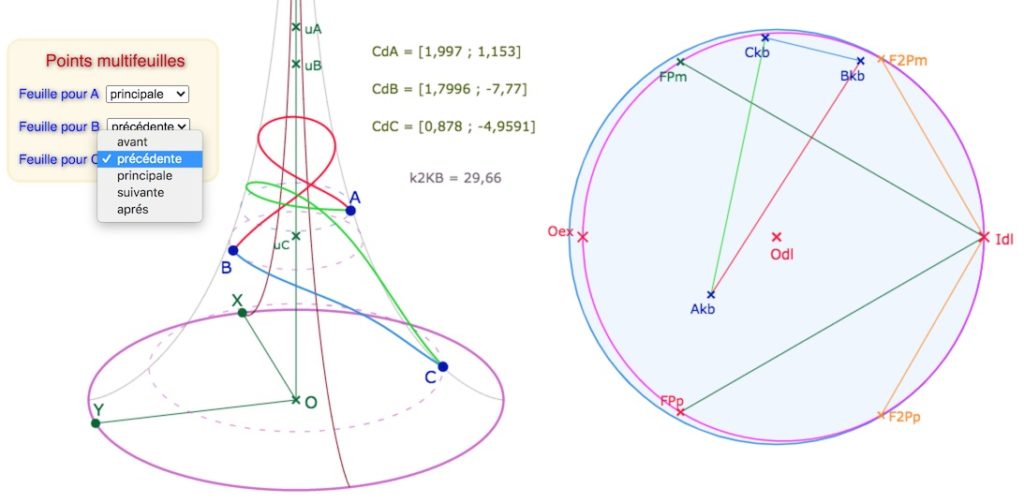
« avant » désigne la feuille « -2 », soit, sur KB des points à droite du segment \([F2P_m \, I_{dl}]\)
« après » désigne la feuille « +2 », soit, sur KB des points à droite du segment \([F2P_p \, I_{dl}]\)
La figure de base
Exploration de la situation de base, en changeant les points de base de feuilles,
et en déplaçant les points ou leurs latitudes. Tourner et pencher la pseudosphère.
Préférer ouvrir cette figure dans un nouvel onglet. Utilisable pour faire soi-même des figures.
Les figures sur les droites ne sont pas extraordinaires. On va donc s’intéresser aux cycles. Le lecteur (très motivé) peut construire le cycle inscrit/exinscrit du triangle podaire d’un triangle, l’orthocentre étant le centre du cercle inscrit, ou le pôle de la perpendiculaire commune des hauteurs quand il est hors du cercle limite. On a renoncé à illustrer cette figure (trop de droites à afficher pour que ce soit vraiment clair).
Quelques illustrations du cercle inscrit d’un triangle
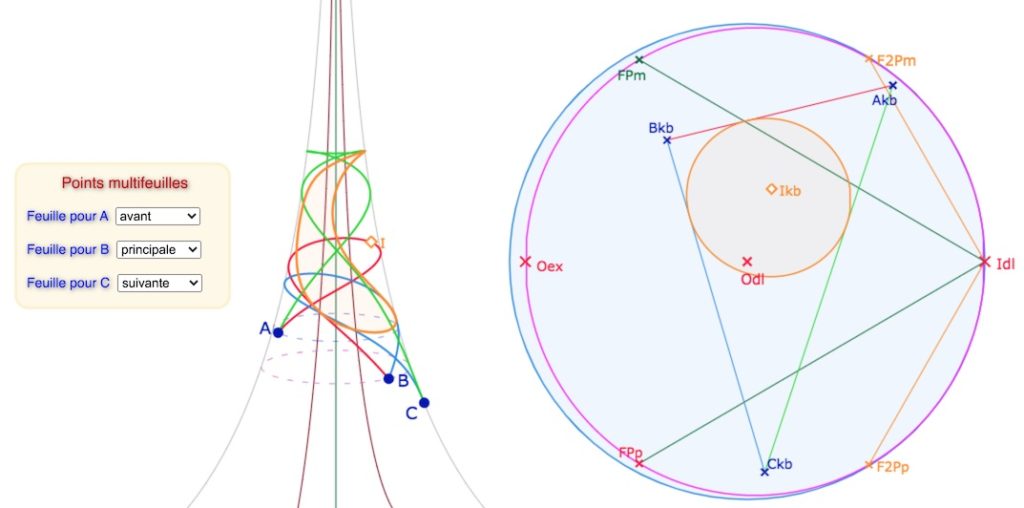
Ci-dessus, un cercle inscrit qui tient dans une feuille – largement – pour un triangle réparti sur 4 feuilles de la surface.
Ci-dessous, un cercle inscrit qui se déploie exactement sur une feuille pour un triangle réparti sur 5 feuilles.
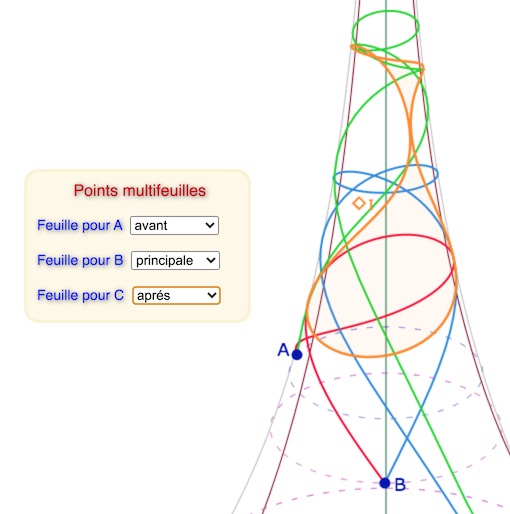
Manipulation de la figure
En plus des manipulations précédentes, penser à déplacer \(O_{ex}\)
pour illustrer l’invariance du cercle inscrit alors qu’il est renvoyé depuis KB.
Préférer ouvrir cette figure dans un nouvel onglet (plus grande, plus facile à manipuler)
La construction de Malfatti multi-feuille
La figure n’est pas si extraordinaire que cela, en particulier il faut manipuler la figure pour vraiment apprécier la configuration. En voici une illustration avec un triangle sur 4 feuilles. Sur la PS, on a ajouté le triangle des centres des cercles pour voir les points de contact de ces cercles deux à deux.
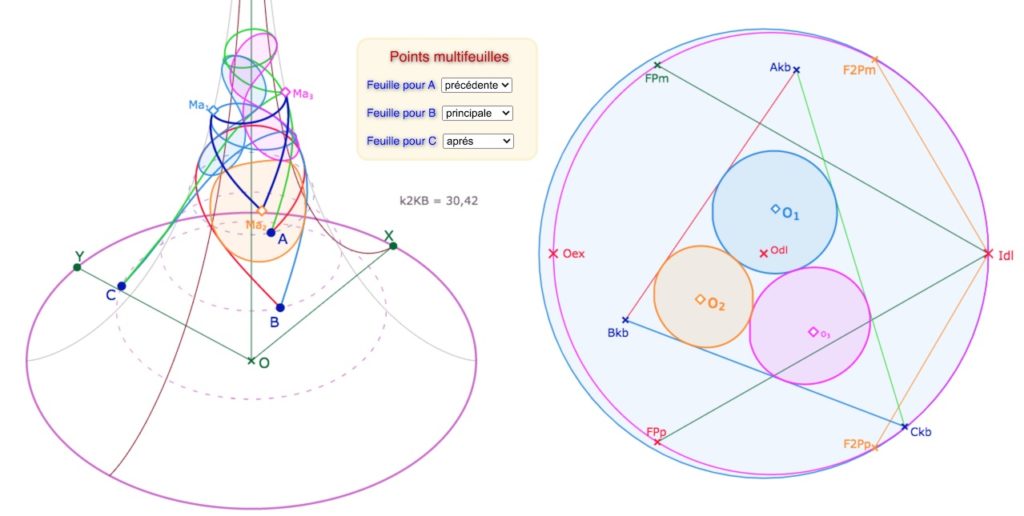
Voici une autre configuration, avec un triangle sur 5 feuilles, et sa vue de dessus
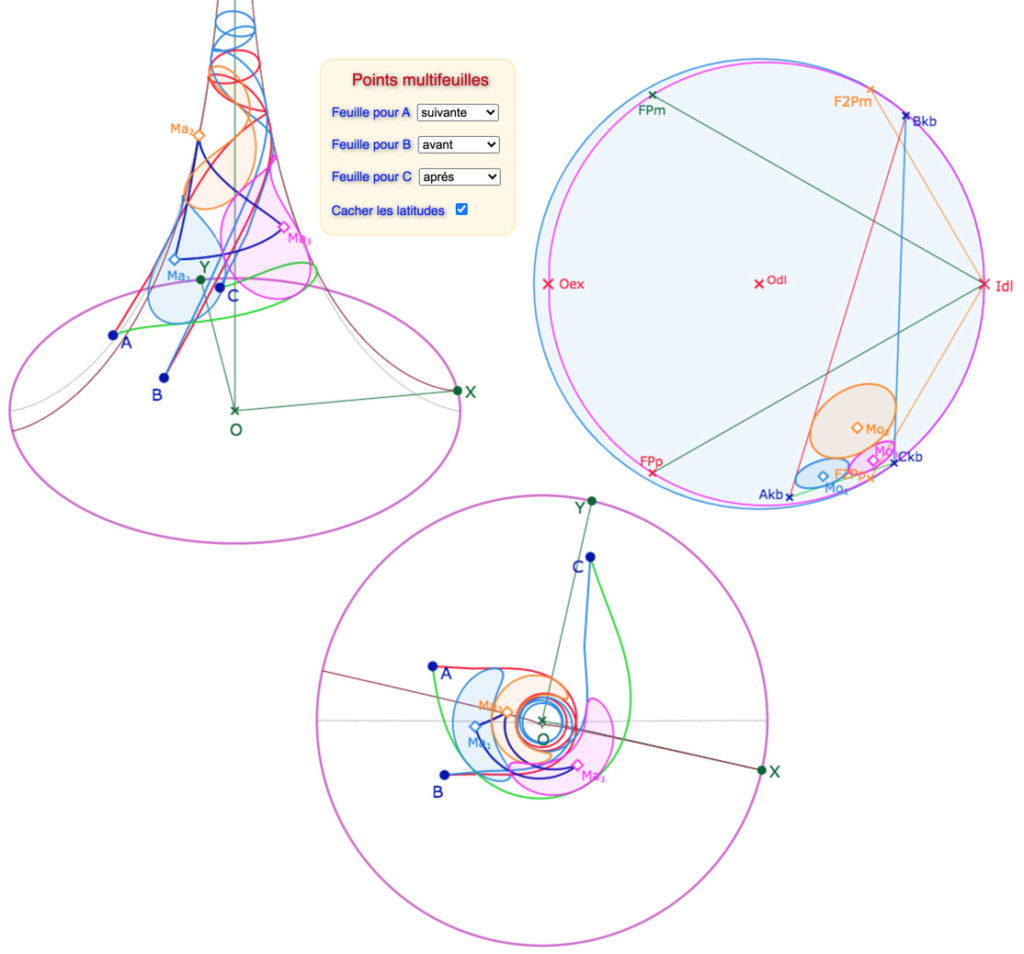
Lancer la figure associée dans un nouvel onglet (chargement rapide)
Cycle circonscrit
On reprend le cycle circonscrit car dans ces configurations, la partie très enroulée peut facilement être celle qui passe par les trois sommets, alors que ce n’était pas le cas dans la figure de la section précédente. Et c’est aussi l’occasion de voir des cercle circonscrits eux aussi très enroulés.
Voici une galerie de douze configurations, six avec un cercle circonscrit, six avec une équidistante.
On peut reproduire facilement les 10 premiers exemples avec la figure ci-dessous
La diapo 6 est proposée pour justifier la prochaine section de programmation
Figure à manipuler
Commencer par changer de feuille les différents points avant de les déplacer, eux, ou leurs latitudes.
Pour que les points soient manipulables les lieux sur la pseudosphère sont densifiés à 1500 (seulement)
Préférer ouvrir la figure dans un nouvel onglet – peut mettre 10 s à s’ouvrir. La figure est plus grande, donc plus facile à manipuler, toutefois avec des lieux plus denses, mais à densité modifiable (dans l’inspecteur d’objets)
Deux autres figures complémentaires … qui peuvent mettre 20 s à s’ouvrir
Figure contenant la configuration 11 de la galerie
Figure contenant la configuration 12 de la galerie
Version programmée d’un cycle circonscrit
proche de l’horicycle
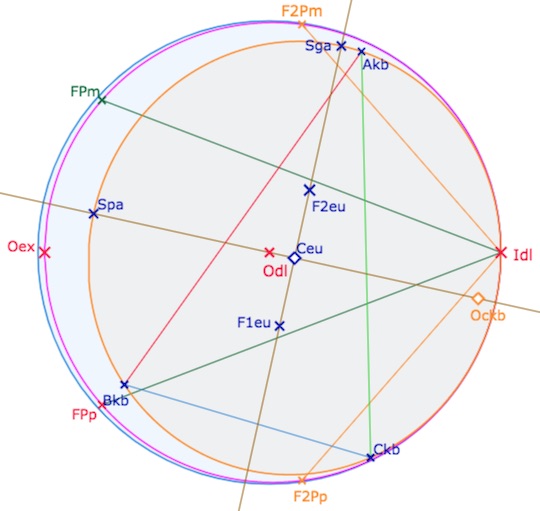
La construction géométrique standard autorise des lieux jusqu’à 5000 objets par lieu. Mais on peut, par programmation, fait des lieux par les listes de segment de taille bien plus grande. Voici comment on peut opérer. Le logiciel permet de récupérer l’axe focal de la conique. On note \(C_{eu}\) le centre euclidien de la conique, \(S_{ga}\) un sommet du grand axe et \(S_{pa}\) un sommet du petit axe.
Pour un paramètre n compris entre 0 et 1000 (par exemple), un point de la conique est donné par \(C_{eu}+(S_{ga}-C_{eu}) \displaystyle \, cos \left(\frac{2πn}{1000}\right)+(S_{pa}-C_{eu}) \, sin \left(\frac{2πn}{1000} \right)\).
Ensuite on renvoie ce point sur la surface, le tout dans une liste de segment. Pour cela on reprend le contenu de la macro de transfert sous forme d’expression-programme :
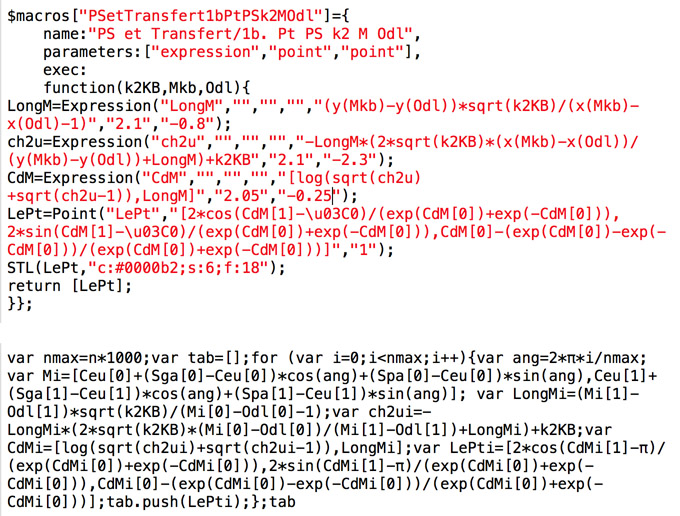
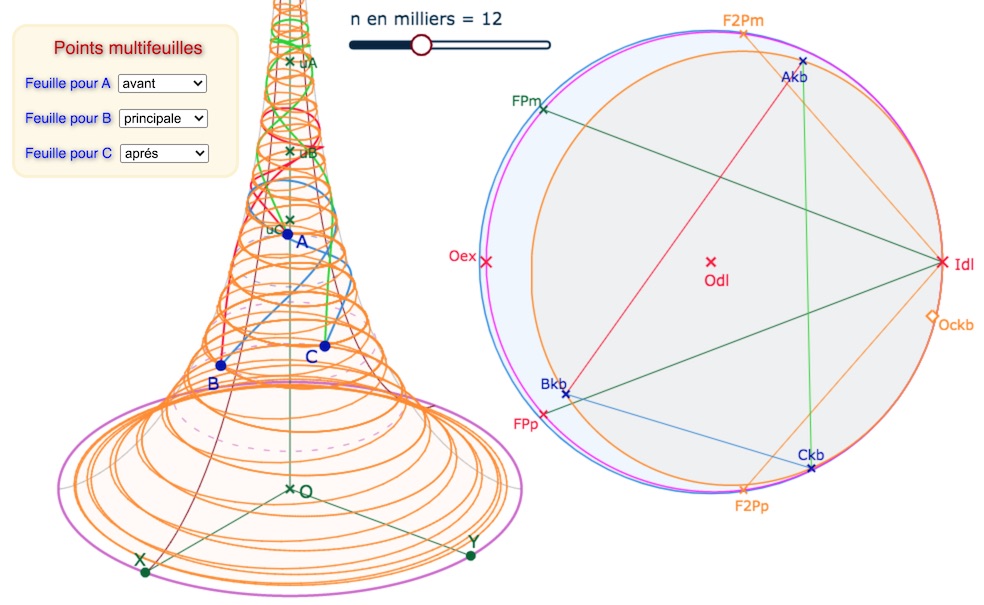
On a choisit un curseur \(n\) qui va de 2 à 30. Le nombre de terme est \(1000n\). Dans la figure enregistrée, n est réglé à 2. Ensuite, après avoir modifié les points du triangle, on augmente la valeur de n. En voici quelques illustrations.
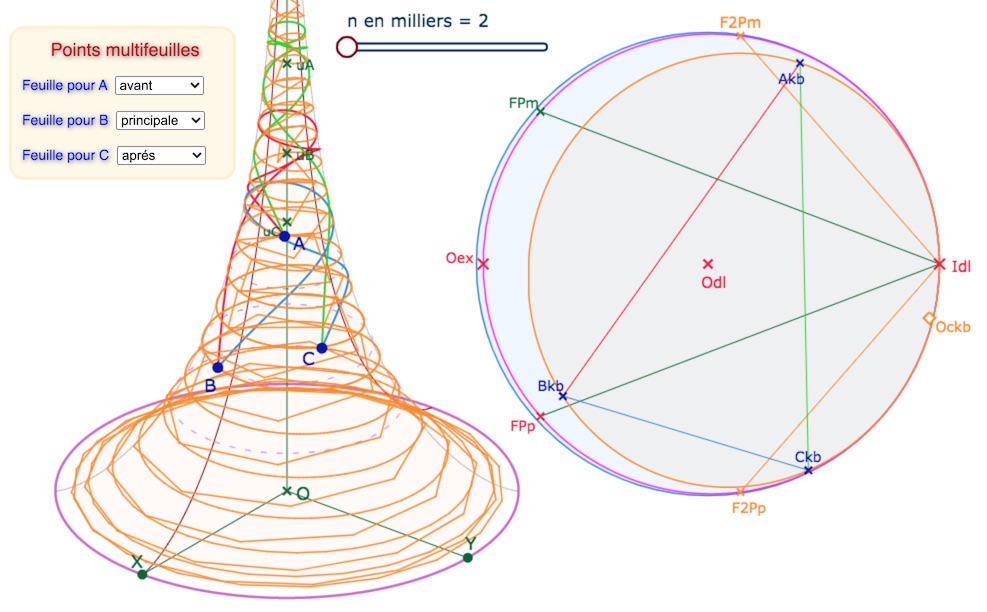
Ci-dessus avec n minimal et ci-dessous, n à 12
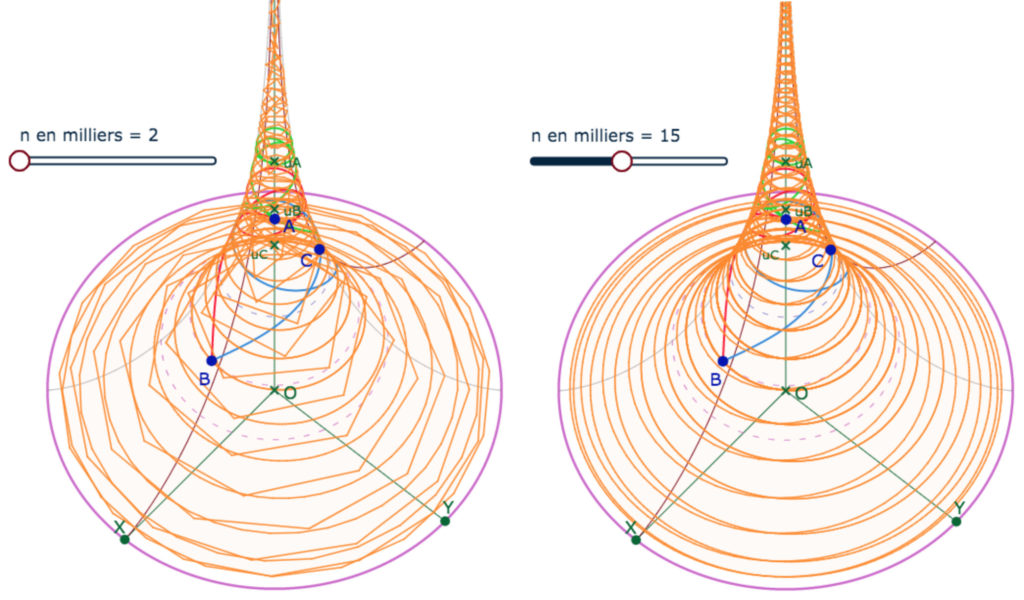
Autre point de vue
Lancer cette première figure dans un nouvel onglet (elle s’ouvre en moins de 10 secondes, plus rapide que les deux précédentes).
En pratique on manipule la figure avec \(n=2\), et quand on a la situation que l’on veut illustrer, on augmente \(n\).
Ajout de l’équidistante par programmation
Dans la figure précédente, l’équidistante est tracée mais par la méthode de la section précédente. On poursuit donc la programmation du cas de l’équidistante. Il suffit d’adapter ce qui précède. On choisit toutefois de pondérer la densité de la liste aux frontières de la surface (les images de \(int_1\) et \(int_2\)) de la façon suivante.
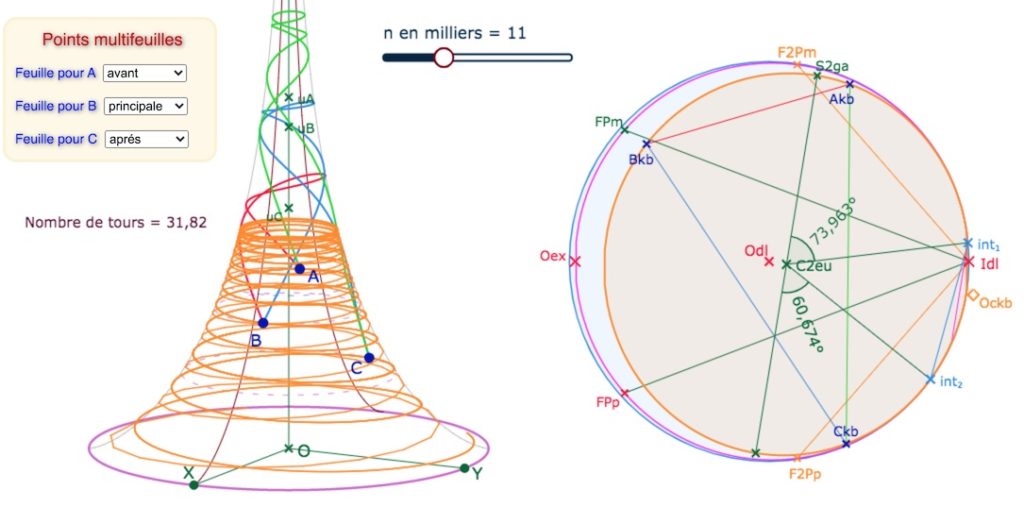
Sur 1000 segments, on en consacre 400 pour la partie entre \(int_1\) et \(S_{2ga}\), 200 pour la partie entre ce point et son symétrique (amplitude \(\pi\) sur le cercle), et à nouveau 400 pour le retour sur \(int_2\). Quand le point \(int_1\) est trop proche de \(L_{dl}\) – le point à l’infini – la figure peut ne pas être correcte, en particulier le cas où \(int_1\) est en dessous de \(L_{dl}\) n’est pas traité. Par ailleurs, on aura compris que seul le cas où \(Oc_{kb}\) se trouve à droite du cercle limite est traité (le cas de « la configuration 12 » précédente n’est pas abordé).
Quand \(int_1\) est vraiment proche de \(L_{dl}\), on voit ci-dessous que même avec la pondération ci-dessus, et avec plus de 20 000 segments, on a encore un visuel saccadé proche de l’horizon :
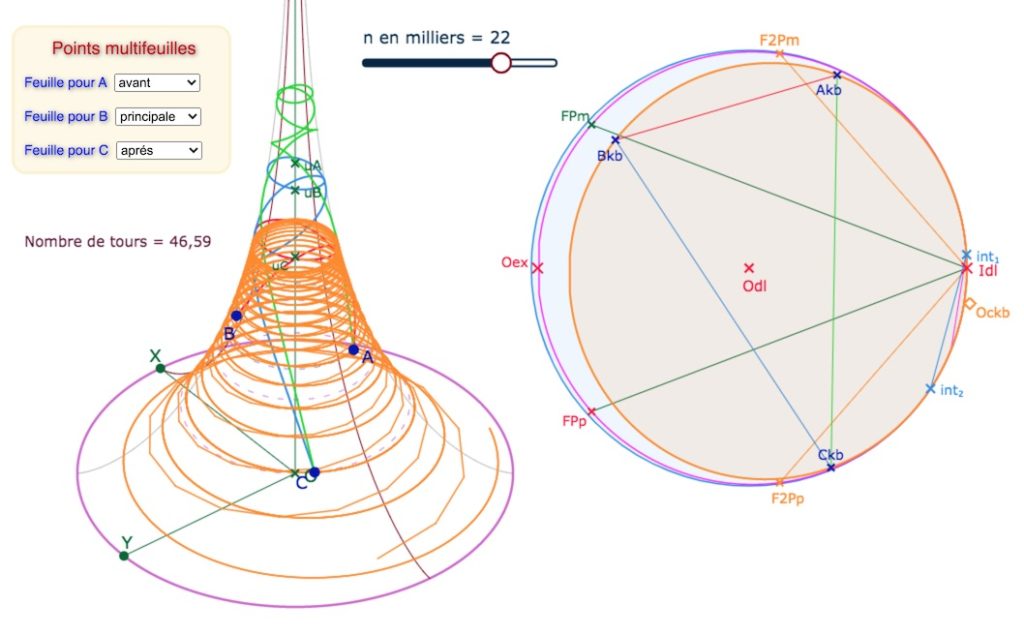
Pour l’équidistante il est facile de compter le nombre de tours. On peut adapter la démarche pour le cercle circonscrit. Toutefois, le nombre de tours obtenu est nécessairement minimisé. La construction du cercle, même proche de l’horicyle, est plus stable que l’équidistante comme on le voit en comparant l’illustration précédente et celle-ci :
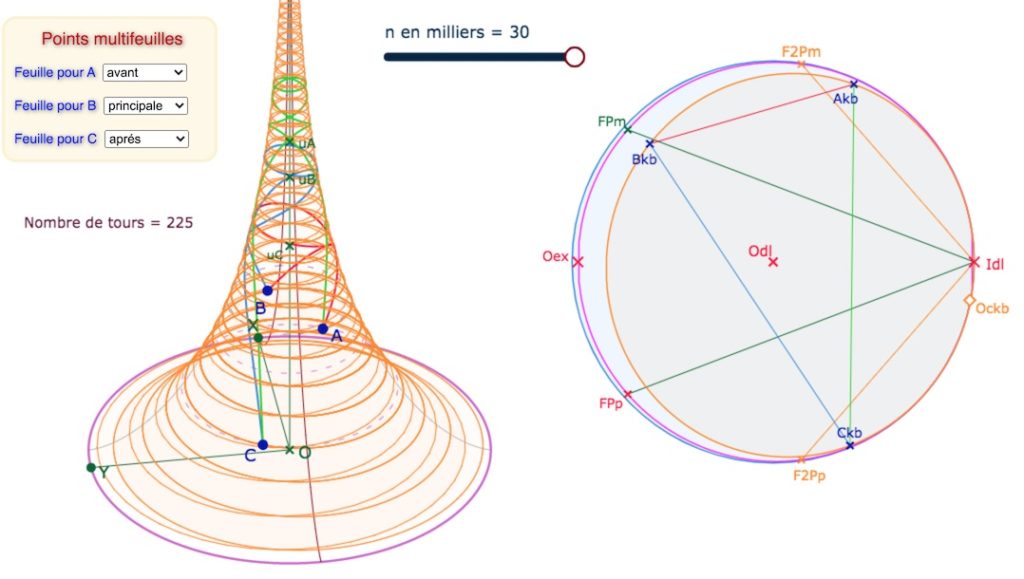
Pour un nombre de tour assez grand, ce nombre est un peu minimisé. Pour des petit nombre de tours,
la valeur affichée est trop faible (par exemple 2 au lieu de 5).
Lancer cette figure finale dans un nouvel onglet (ouverture sur l’équidistante)
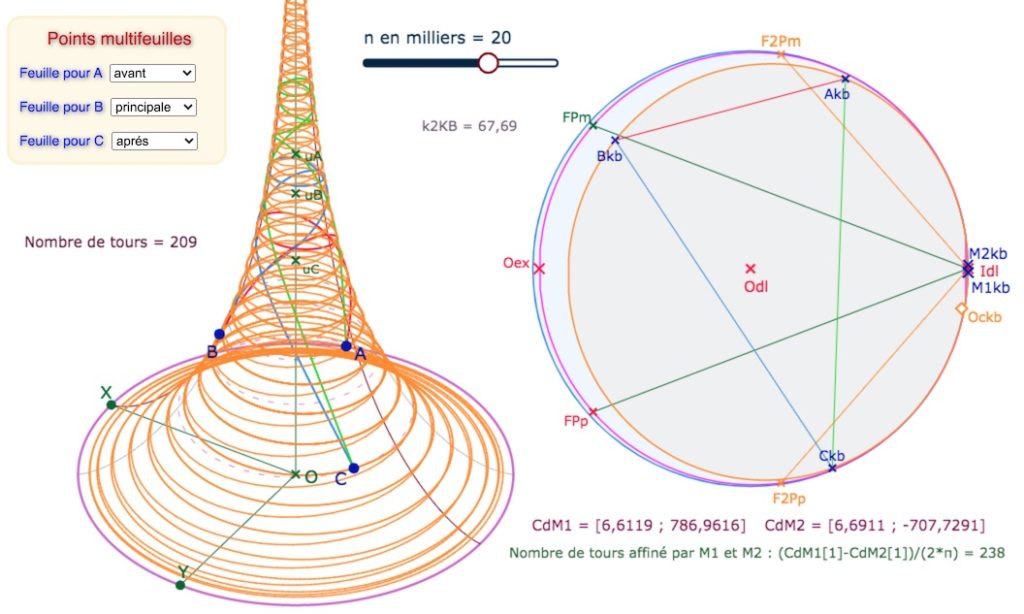
Essai d’optimisation du nombre de tours en prenant deux points sur le cercle \(M_{1kb}\) et \(M_{2kb}\)
Ci-dessous, même configuration vue de dessus et d’une partie de la latitude nécessaire (6,69)
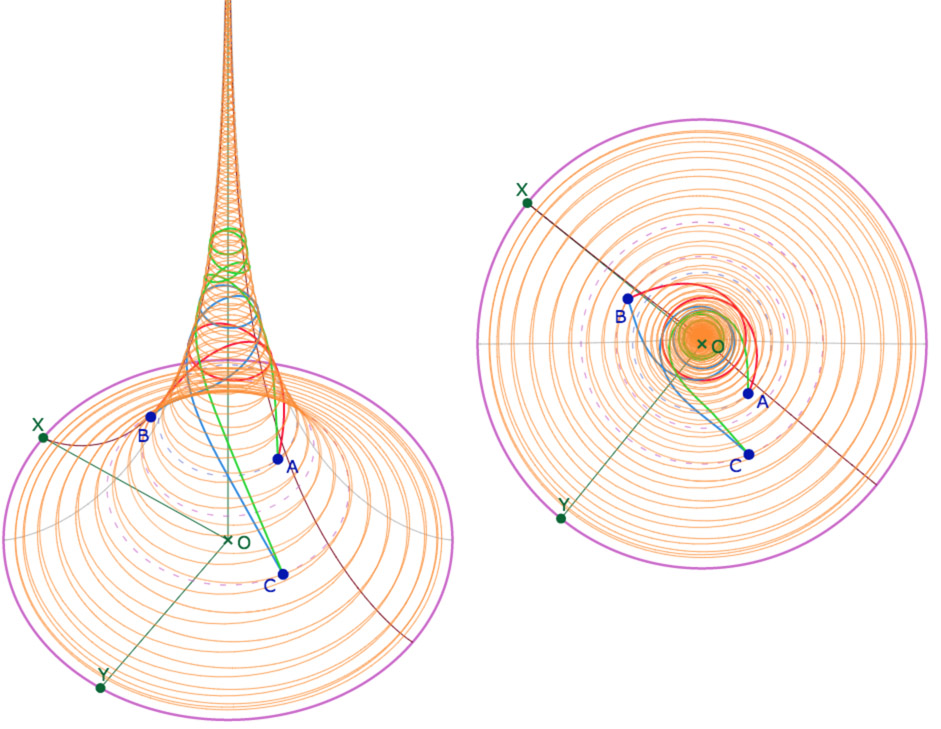
Lancer la figure ci-dessus dans cette configuration (quelques secondes d’ouverture)