Après avoir illustré la première partie du mémoire de Janos Bolyaï, nous abordons maintenant la partie consacrée à la constructibilité des segments, et à la quadrature du cercle en géométrie hyperbolique. Il est le seul à son époque à s’intéresser à cette question, et son résultat est largement passé inaperçu avant d’être redécouvert à l’occasion de la publication de la correspondance de Gauss.
Construction de \(\Pi(x)\) et \(\Delta(\alpha)\)
Cette seconde partie commence par la construction de l’angle de parallélisme (§ 34). Bolyaï met en évidence – de manière intrinsèque, hyperbolique – la construction suivante, très simple, justifiée par les résultats des § 25 et § 27.
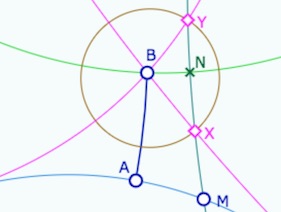
Angle de parallélisme \(\mathbf{\Pi(AB)}\)
Depuis \([AB]\), on mène les perpendiculaires en \(A\) et \(B\), notons les \(\Delta_A\) et \(\Delta_B\). Depuis un point \(M\) de \(\Delta_A\) – on rappelle que Bolyaï ne travaille en fait que sur des demi-droites – on même la perpendiculaire à \(\Delta_B\) qu’elle coupe en \(N\). Le quadrilatère \(AMNB\) a trois angles droits, et un angle aigu (en \(M\)).
Alors le cercle de centre \(B\) et de rayon \(AM\) coupe le segment \([MN]\), en un point \(X\) tel que \([BX)\) est parallèle à \([AM)\). Bolyaï prend soin de montrer l’existence de points \(M\) sur \(\Delta_A\) pour que ce point d’intersection \(X\) existe.
Illustration du parallélisme dans le modèle DP …
où l’on voit les points idéaux, et donc « confirme » – illustre bien – que les droites sont parallèles.

On notera aussi que le cercle coupe la droite \((MN)\) en un second point \(Y\) tel que
la droite \((BY)\) est la seconde parallèle à \((AM)\) issue de \(B\).
Bolyaï ne parlent pas de cette seconde parallèle car il ne travaille « que d’un côté », n’utilisant que des demi-droites. Cette construction est aussi celle de la parallèle (d’un côté) à une droite issue d’un point, propriété utilisée dans la construction suivante.
Construction du segment \(\mathbf{\Delta(a)}\)
Voyons maintenant la construction (§ 35) de la longueur \(\Delta(a)\). On se donne un angle \(\angle a = mAn\), on veut construire sur \([Am)\) un point \(S\) tel que l’angle de parallélisme de \(AS\) soit \(a\), soit \(\Delta(a)=AS\).
Soit \(B\) un point quelconque sur \([Am)\). Notons \(K\) le pied de la perpendiculaire à \([An)\) issue de \(B\). Par la construction précédente on sait tracer la parallèle à \([An)\) issue de \(B\) du côté de \(n\). C’est la demi-droite \([Bb_1)\). Bolyai montre alors que l’on peut toujours prendre \(B\) sur \([Am)\) pour que la droite\((BK)\) et la perpendiculaire à \([Bb_1)\) passant par \(A\) soient sécantes. Soit \(H\) cette intersection.
Alors le pied de la perpendiculaire à \([Am)\) issue de \(H\) est le point \(S\) cherché.
On voit ci-dessous que cette perpendiculaire est aussi parallèle à \([An)\) et \([Bb_1)\) ce que montre aussi Bolyaï.
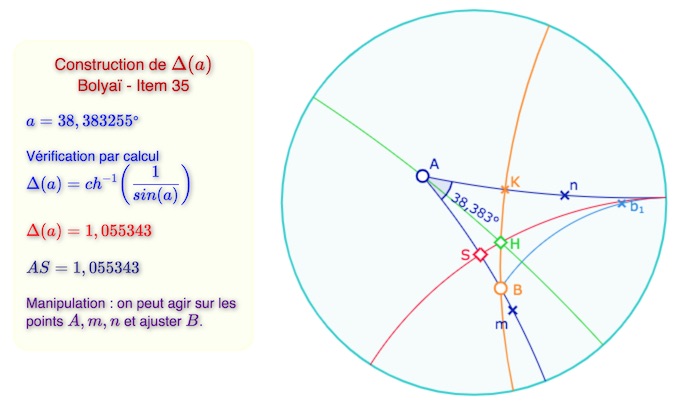
Les vérifications numériques sont assurément inutiles :
la construction est fondamentalement celles de l’orthocentre d’un triangle ayant un point idéal.
Lancer la figure associée à cette illustration dans un nouvel onglet.
Cette construction est conceptuellement plus délicate que celle du § 34, en particulier car il s’agit d’un résultat sur un triangle idéal (ayant au moins un sommet à l’infini) ou encore – avec notre lecture contemporaine – sur le pinceau des hauteurs d’un trilatère – concept très éloignés des débuts de la géométrie hyperbolique
La principale difficulté est d’assurer l’existence de l’intersection des deux hauteurs. Le fait que Bolyai l’étudie et en donne une caractérisation montre qu’il a une vision très claire de la situation – on pense naturellement à certaines constructions de Legendre. Dit avec un regard contemporain, la position limite, quand l’orthocentre est le point idéal « de l’autre côté » est réalisée quand \(\angle kAm\) est l’angle de parallélisme … du pied de la hauteur idéale rose ci-dessous. D’où son résultat.
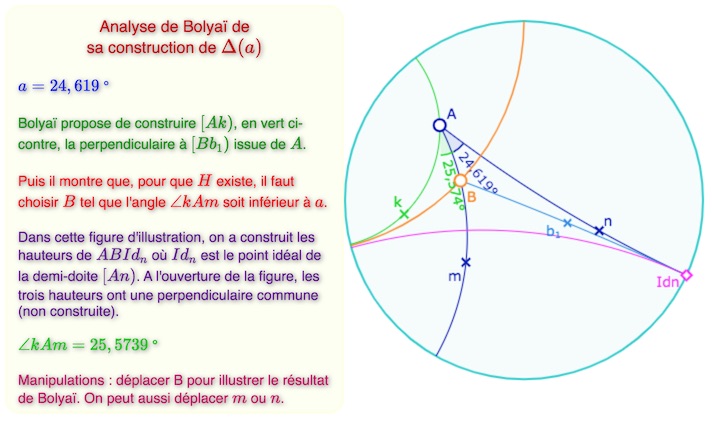
Lancer la figure associée à cette illustration dans un nouvel onglet.
Nous avons illustré ici les constructions de Bolyaï qui sont « hyperboliques » au sens de indépendantes d’un modèle dans lequel on travaille. Bien entendu, dans un modèle, comme celui du disque de Poincaré où on a directement accès à l’infini, les constructions de \(\Pi(x)\) et de \(\Delta(a)\) sont bien plus simples et immédiates.
Constructivité des segments
On commence par revenir sur la problématique du calcul de l’expression \(X\) égal au rapport de deux arcs parallèles d’horicycles concentriques.

Rappel de la situation présentée dans l’article précédent
Lancer la figure associée à cette illustration dans un nouvel onglet.
Pour traiter l’aspect constructif des segments, Bolyaï se place désormais dans le cas où l’angle \(u\) est droit. Alors l’angle \(v\) devient un angle de parallélisme, et compte tenu des calculs réalisés en fin de la première partie, on peut désormais écrire :
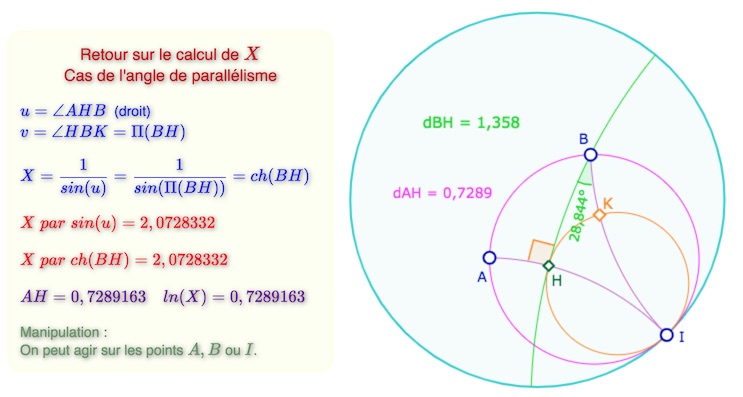
Dans cette figure on considère l’horicycle de centre \(I\) passant par \(A\). \(B\) est un point de cet horicycle.
Puis on construit \(H\) le pied de la perpendiculaire à \([AI)\) issue de \(B\). La parallèle à \([AH)\) passant par \(B\)
coupe l’horicycle concentrique au premier, passant par \(H\) en \(K\).
Rappel : la référence au \(ln(X)\) n’est pas explicitement dans le mémoire de Bolyaï
Lancer la figure associée à cette illustration dans un nouvel onglet.
Premier exemple de constructibilité
Dans les paragraphes suivants (le § 36 comme lemme, puis le § 37) Bolyaï explique comment, en utilisant le théorème de Thalès sur l’horisphère, il peut construire un point particulier sur un horicycle, pour peu que son correspondant soit \(\Sigma\)-constructible sur l’horisphère. Ce paragraphe 37 se termine ainsi :

Bolyaï – Fin du § 37 (dans la traduction de Jules Hoüel)
Rappel : \(L\) désigne des horicycles, \(F\) des horisphères et \(R\) est l’angle droit.
Et donc l’angle \(\displaystyle \frac{\pi}{6}\) est \(S\)-constructible car il est \(\Sigma\)-constructible. Bolyaï propose alors la construction suivante :
\(AH\) est \(S\)-constructible ssi les éléments de l’horicycle se sont.
Or, Ici \(\displaystyle X=ch(BH)= \frac{1}{sin(B)}=2\) est \(\Sigma\)-constructible, donc \(AH\) est \(S\)-constructible.
Caractérisation de la \(S\)-constructivité des segments
On retient traditionnellement de son mémoire, cette caractérisation même si elle n’est pas exprimée de cette façon :
Un segment de longueur \(r\) est \(S\)-constructible ssi \(sh(r)\) est \(\Sigma\)-constructible.
Les formules de trigonométrie hyperbolique permettent d’exprimer la caractérisation indifféremment avec \(ch(r)\) ou même \(e^r\). Bien entendu c’est aussi équivalent à \(\displaystyle sh \left( \frac{r}{2} \right)\) \(S\)-constructible car on passe de\(sh(r)\) à \(\displaystyle sh \left( \frac{r}{2} \right)\) par des relations constructibles (second degré).
La \(S\)-quadrature du cercle
La \(S\)-quadrature consiste à construire d’une part, un cercle d’aire \(\pi\) et d’autre part construire un carré de même aire. La situation hyperbolique est bien différente de la situation euclidienne.
Les \(S\)-carrés ne sont pas des quadrilatères ayant 4 angles droits, cela n’existe pas, mais des quadrilatères ayant les côtés de même longueur et les mêmes angles aux sommets. Il existe des carrés de tout angle compris – strictement – entre 0 et 90°.
Bolyaï montre, après plusieurs précurseurs, mais avec sa propre démarche, que l’aire d’un triangle est ce que l’on appelle le défaut d’angle, \(\pi-\hat{A}-\hat{B}-\hat{C}\), et donc qu’un carré d’aire \(\pi\) est un carré d’angles aux sommets \(\displaystyle \frac{\pi}{4}\).
L’angle est constructible, mais le problème n’est pas là : qu’en est-il du côté du carré ?
Prélude à la \(S\)-construction d’un cercle d’aire \(\pi\)
On rappelle que l’aire du disque de rayon \(r\) est \(4\pi \displaystyle sh^2 \left( \frac{r}{2} \right)\) (montré au § 32). Ainsi un disque d’aire \(\pi\) a pour rayon \(r_0\) tel que \(\displaystyle sh \left( \frac{r_0}{2} \right)=\frac{1}{2}\). Donc \(r_0\) est constructible. Bolyaï va même aller jusqu’à proposer une construction effective de \(r_0\) par une transformation particulièrement astucieuse.
Transformation d’un arc d’horicycle en angle
Dans un premier temps, il montre que l’arc d’horicycle allant de \(A\) à \(B\) à pour longueur \(\displaystyle 2 sh \left( \frac{AB}{2} \right)\).
Remarque : Bolyaï parle de « l’arc d’horicycle », alors qu’il y a deux horicycles passant par \(A\) et \(B\). Cela vient du fait que travaillant sur des demi-droites, il n’a « qu’un côté du plan ». Mais en fait la droite \((AB)\) est axe de symétrie du plan hyperbolique qui échange les deux horicycles.
« Construction de l’horicycle » passant par deux points \(A\) à \(B\)
Par « construire un horicycle », on entend ici – pour rester dans l’esprit de BolyaÏ – simplement construire les deux parallèles en \(A\) et \(B\) qui caractérisent cet horicycle … et qui vont être utiles dans les constructions suivantes. Pour cela, il suffit de prendre le milieu des deux points – qui se construit avec la médiatrice de ces deux points, par intersection de deux cercles – et ensuite construire, par § 34, en \(A\) et \(B\), l’angle de parallélisme \(\displaystyle \Pi \left( \frac{AB}{2} \right)\).
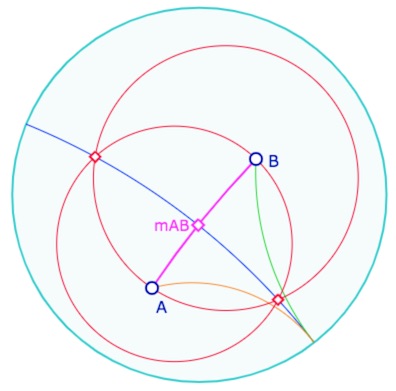
Ensuite, Bolyaï construit un angle \(\theta\) tel que \(tan \, \theta = \displaystyle 2 sh \left( \frac{AB}{2} \right)\) de la manière suivante :
On se donne donc deux points \(A\) et \(B\) et on considère « l’horicycle » par ces deux points comme ci-dessus. Dans la figure suivante, on a noté \(I\) le centre de cet horicycle, pour simplifier l’écriture des demi-droites (éviter d’ajouter des points pour écrire \([Am)\) ou \([Bm)\) comme dans le texte de Bolyaï), mais bien entendu ce n’est pas utile dans la construction.
On construit la perpendiculaire à la demi-droite \([AI)\) issue de \(B\) que l’on nommera \((BH)\) puis la perpendiculaire à cette droite passant par \(B\). On note [BX) la demi-droite du même côté que les autres demi-droite (toujours pour rester dans l’esprit de Bolyaï). Alors la tangente de l’angle \(\theta =\angle IBX\) est égale à l’arc d’horicycle passant par \(A\) et \(B\), soit \(\displaystyle 2 sh \left( \frac{AB}{2} \right)\).
Dans cette figure, déplacer simplement les points \(A\) ou \(B\)
Compte tenu des relations trigonométriques vues à l’article précédent, sur l’angle de parallélisme, et dans le triangle rectangle, la preuve de cette transformation est assez élémentaire :
\( tan \, \theta =\displaystyle \frac{1}{tan \left( \frac{\pi}{2}-\theta \right)} = \frac{1}{tan \left( \Pi(AH) \right)} = sh \left(AH \right)\)Or le triangle \(ABH\) est rectangle en \(H\). On peut donc écrire
\(\displaystyle sh(AH) = sh(AB) \; sin \left( \Pi \left( \frac{AB}{2} \right) \right)\), car, comme on l’a vu dans l’illustration de la « construction de l’horicycle », l’angle \(\angle ABI\) est \(\displaystyle \Pi \left( \frac{AB}{2} \right)\).
Enfin, par \(sin \; \Pi(x) = \displaystyle \frac{1}{ch(x)}\), et \(sh \, 2t = 2 sh \, t \; ch \, t\), on a bien \(tan \, \theta = \displaystyle 2 sh \left( \frac{AB}{2} \right)\).
Construction un disque d’aire \(\pi\)
Bolyaï utilise la construction précédente, mais à l’envers, en partant de l’angle \(\theta\) particulier qui permet cette construction. Voici, dans une figure, un résumé de la démarche :
Préférer ouvrir cette figure dans un nouvel onglet
Construction un carré d’aire \(\pi\)
Reste la constructibilité d’un carré d’aire \(\pi\), c’est-à-dire d’angle au sommet de \(\pi\)/4. Bolyai décompose alors le carré à construire en 8 triangles rectangles d’angles \(\pi\)/4 et \(\pi\)/8, de la façon suivante.
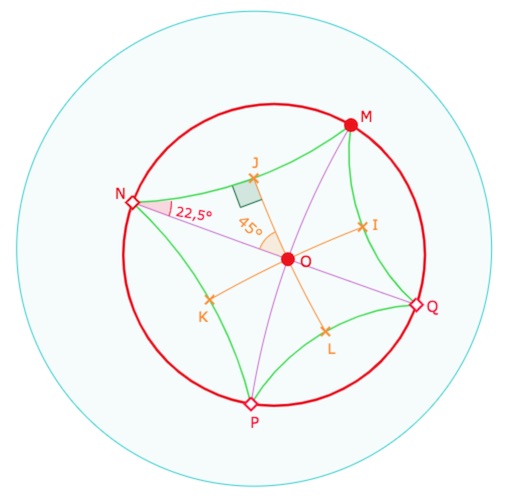
Construire un carré d’aire \(\pi\) revient à construire un triangle rectangle
d’angles \(\pi\)/4 et \(\pi\)/8.
Bolyaï montre, en calculant sa longueur, que le côté opposé à l’angle de 45°; le côté \(x=NJ\), est constructible. Il écrit (\(R\) désigne l’angle droit) :
Soient [les angles] cab =R, acb =R/2, abc =R/4 et ac = x.On pourra exprimer X (§ 31.II) par de simples racines carrées et le construire (§ 37). Connaissant X, on pourra déterminer x (§ 38 ou encore § 29 et § 35). L’octuple du triangle abc est [a pour aire] évidemment π, et, par là un cercle plan se trouve carré géométriquement au moyen d’une figure rectiligne et de lignes uniformes de même espèce(*) (c’est-à-dire de lignes équivalentes à des droites quant à leur comparaison entre elles).
La science absolue de l’espace – Bolyaï – $ 43
(*) Les « lignes uniformes de même espèces » sont des horicycles
Concrètement, avec son vocabulaire, Bolyaï utilise une des formules de trigonométrie du triangle rectangle, à savoir ici, avec les notations de l’illustration précédente, \(ch(x)= \displaystyle \frac{cos \, \hat{O}}{sin \, \hat{N}}= \frac{cos \, \pi/4}{sin \, \pi/8} = \frac{\sqrt{2}} {\sqrt{2-\sqrt{2}}}\).
Cela achève, pour lui, la question de la quadrature du cercle car il a construit le disque d’aire \(\pi\) et il vient de montrer que le (demi-)côté du carré d’aire \(\pi\) est constructible. Par contre il ne propose pas de construction effective du carré comme on l’illustre dans la figure suivante.
Dans cette figure, toutes les quantités mesurées sont réévaluées pendant l’animation
On peut déplacer le centre du cercle pendant l’animation (que l’on peut aussi annuler et relancer)
Préférer ouvrir cette figure dans un nouvel onglet.
Un prochain article abordera les constructions des triangles rectangles d’angles donnés, et même d’un triangle à partir de ses trois angles, proposées par les successeurs de Bolyaï. En effet, une fois que le mémoire de Bolyaï a été connu, autour de 1860, plusieurs auteurs se sont intéressés assez rapidement à ces questions, et ont développé des techniques de plus en plus efficaces. Par ailleurs, en même temps, on a disposé de plusieurs modèles, d’abord celui de Beltrami, et ensuite les modèles conformes de Poincaré.
Bolyaï termine son mémoire en étendant explicitement sa démarche à d’autres polygones réguliers que le carré (en référence aux résultats de Gauss). Il termine son mémoire par ce paragraphe

Dernier paragraphe du § 43 qui termine le mémoire de Bolyaï
La quadrature du cercle correspond au cas particulier \(tan^2 \; z = 1.\)
Au moment de la publication du mémoire, la condition de Gauss était seulement suffisante,
elle est devenue une caractérisation en 1837 avec le théorème de Wantzel
Voici un exemple (hors mémoire de Bolyaï) de cette extension avec la « pentature » et « l’hexature » de \(\pi\) : constructions – à la règle et au compas – de polygones réguliers d’aire \(\pi\). Un polygone régulier de \(n\) côtés a pour aire \((n-2)\pi-\Sigma \, angles\). Ainsi un pentagone régulier a pour aire \(\pi\) si ses angles au sommets sont égaux à \(\displaystyle \frac{2\pi}{5}\), et un hexagone, si ses angles au sommet sont droits.
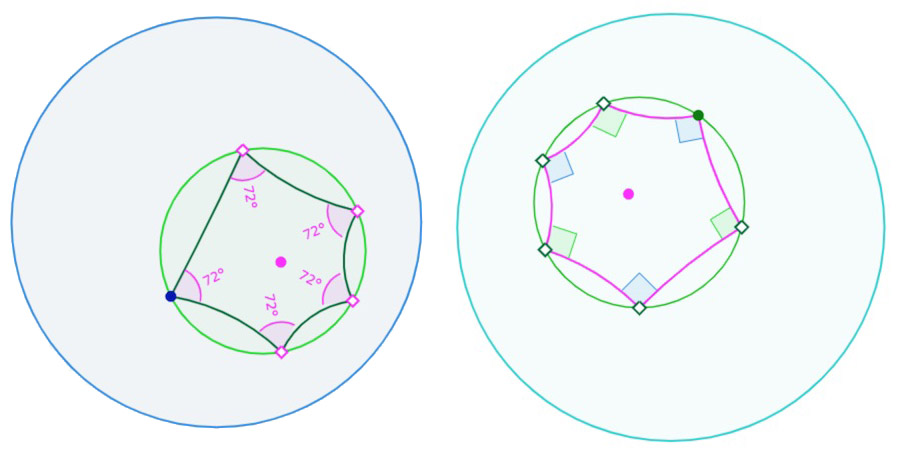
Aperçu des prochains articles sur la constructibilité des polygones réguliers … et des cercles de pavage
L’article intitulé cercles de pavage traite de ces thèmes et propose des figures à « pavages multiples »
Génération 1 de P64 avec remplissage des hexagones