En se posant la question des tangentes à un cercle en géométrie elliptique dans le modèle de Klein, on revient à des problèmes classiques de constructions géométriques … ou presque …
En effet un cercle elliptique a comme support un cercle euclidien. Une tangente elliptique étant un arc de cercle euclidien, son centre est un point à égal distance d’un cercle euclidien et d’un point .
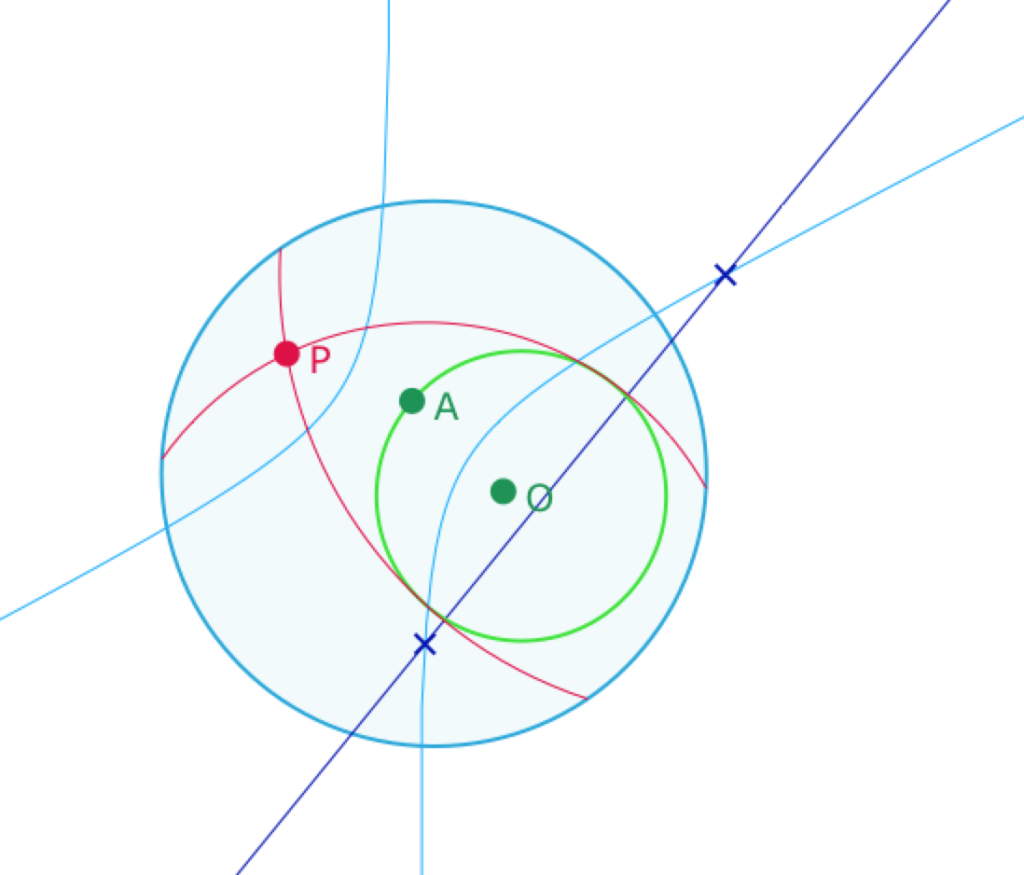
On sait que le lieu des points équidistants d’un point et d’un cercle est une conique. C’est même précisément la conique de cercle directeur ce cercle et de foyer le point en question (l’autre foyer étant le centre du cercle).
Une macro-construction « conique par cercle directeur et foyer », appliquée au cercle euclidien support du cercle elliptique (ci-contre c’est le même) et au point P donne l’hyperbole bleue : le lieu des centres des cercles tangent au cercle vert et passant par P.
Il y aura une tangente au cercle quand la droite (qui assure que le cercle va être une droite elliptique) et la conique (qui assure qu’il sera tangent au cercle support) sont sécantes. Comme une droite rencontre deux fois au plus une conique, il y a bien, comme dans le cas euclidien, en général 2 tangentes en P au cercle elliptique.
Problème classique … ou presque, voyons pourquoi …
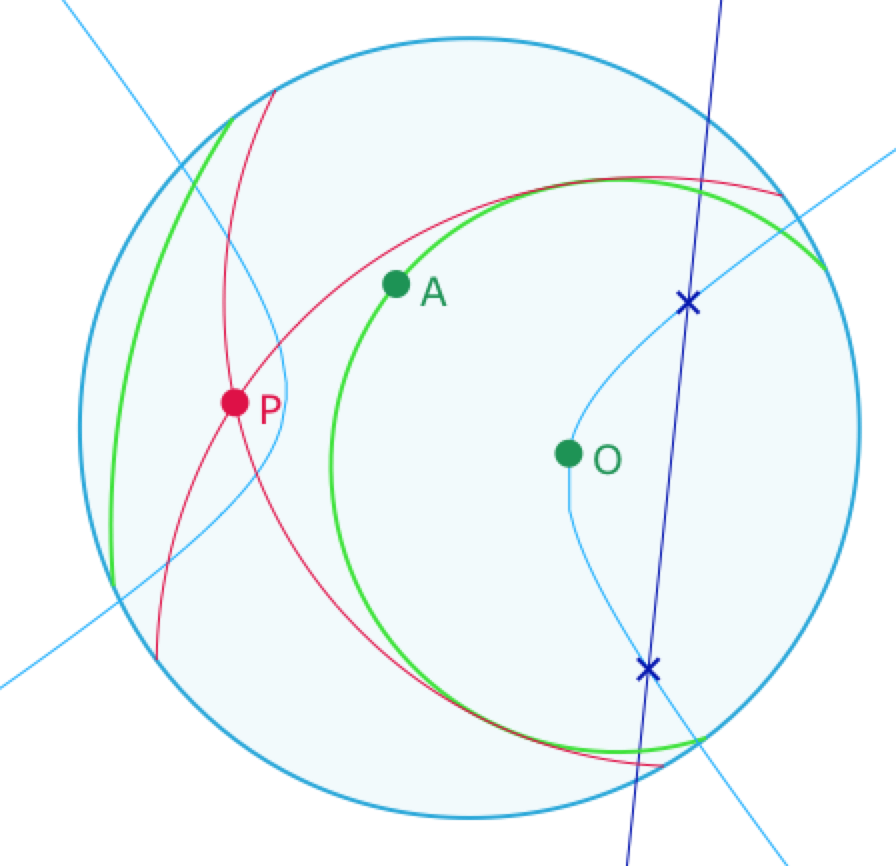
Quand le cercle elliptique est représenté dans le modèle par deux arcs de cercle, la partie extérieure au cercle est la partie entre les deux arcs, comme ci-contre.
On a donc bien encore une hyperbole coupée par par une droite ce qui donne deux tangentes.
On sait que le lieu des points équidistants d’un cercle et d’un point est une hyperbole quand le point est extérieur au cercle et une ellipse quand le point est intérieur au cercle.
On pourrait penser, par réflexe euclidien, que la conique ne peux donc jamais être une ellipse puisqu’il ne peut y avoir de tangente à un cercle par un point à l’intérieur du cercle.
Mais la situation elliptique est plus subtile, car le cercle support peut porter l’arc le plus «euclidiennement éloigné» du centre elliptique. Dans ce cas, le point P, entre les arcs de cercle, peut être à la fois elliptiquement à l’extérieur du cercle et euclidiennement à l’intérieur du cercle support.
Alors le lieu des cercles tangents est une ellipse, comme ci-dessous, et ce qui aboutit encore deux solutions.

En fait que la conique soit une hyperbole ou une ellipse n’a aucune importance ici car la situation est fondamentalement projective (dualité entre points et droite, pôle et polaire), qui ne différencie pas les types de conique.
On peut agir sur les points O, A et P.