Pentagone régulier associé

En manipulant la dernière figure sur les cercles circonscrits de la page sur les cercles elliptiques, on s’aperçoit que l’on peut assez facilement arriver à faire passer – visuellement du moins – le cercle de centre pA par exemple par les deux autres centre pB et pC des cercles circonscrits. On peut alors se poser la question de la simultanéité de cette propriété pour les trois cercles.

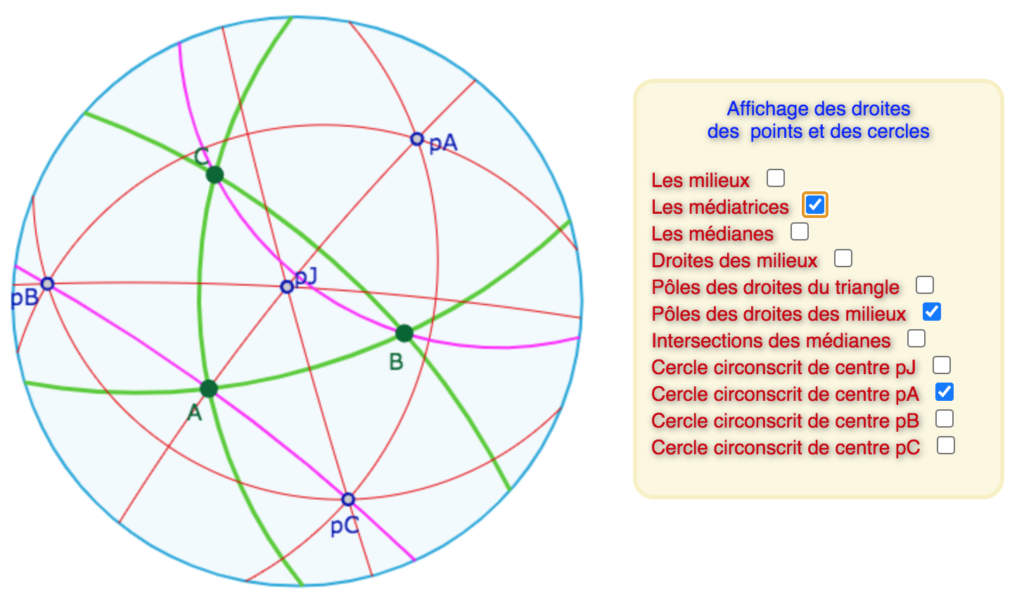
En faisant la construction avec un triangle équilatéral, l’exploration peut être plus fine. Tout d’abord pour un triangle équilatéral, une médiatrice est une hauteur et donc axe de symétrie du triangle. Cette figure comporte alors de nombreuses propriétés.

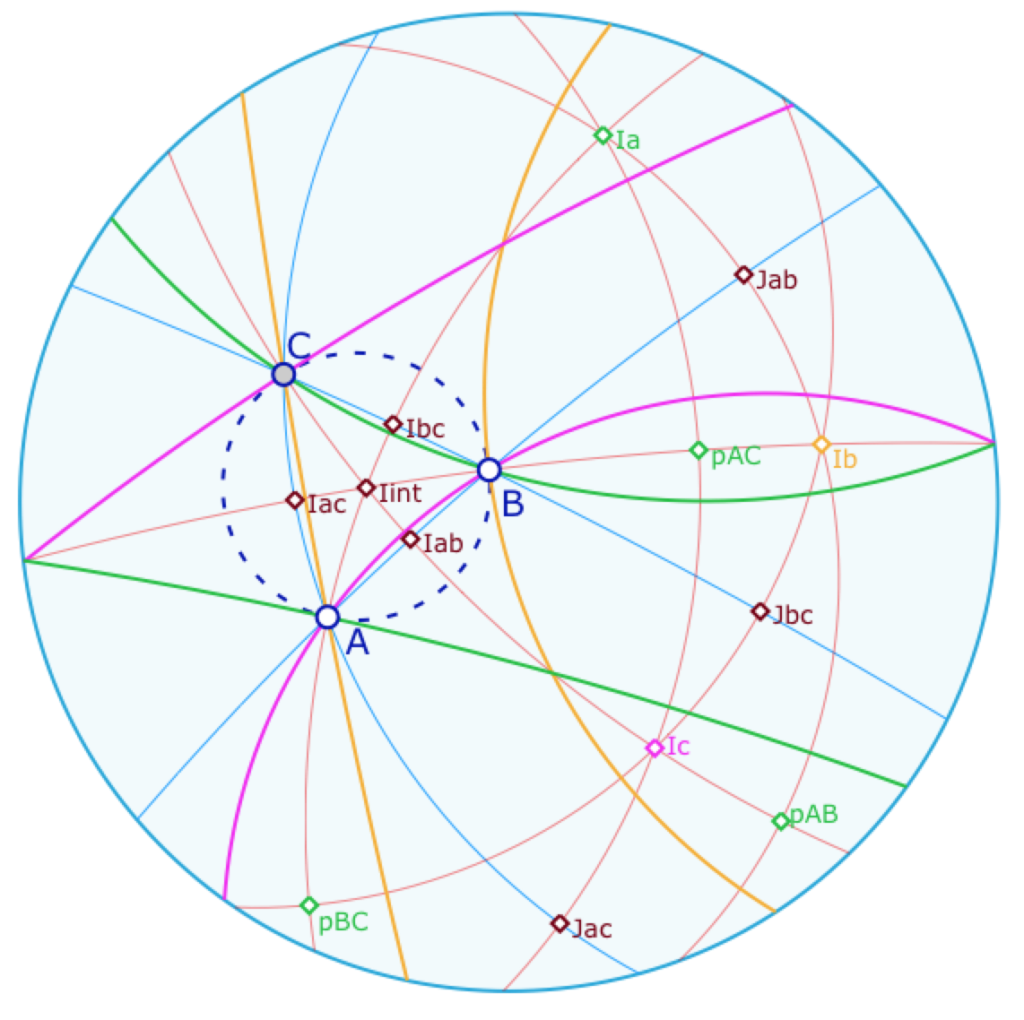
a – Les cercles circonscrits « extérieurs » sont tangents au cercle circonscrit « intérieur ». En effet les centres des cercles (Iint et par exemple Ic) étant sur une médiatrice sont sur un axe de symétrie passant par un sommet du triangle : les deux cercles circonscrits sont nécessairement tangents en ce sommet (pour le cercle de centre Ix en X, avec X =A, B, ou C).

b – Les milieux extérieurs Jab, Jbc et aJc sont équidistant d’une distance de 60° (ils ne forment pas un triangle équilatéral car ils sont alignés. (preuve : car les médiatrices sont deux à deux à 60° – par composition rotation de 120° de centre Iint – et sont axe de symétrie des côtés).

c – Les trois centres Ia, Ib et Ic forment un triangle équilatéral

pour les mêmes raison et de plus, eux, ne sont pas alignes.

d – Les pôles pXY et les milieux Jxy sont les deux milieux des centres de cercle circonscrit Ix et Iy.

La figure avec des possibilités de vérifications

Les cercles circonscrits de centres Ia, Ib ou Ic sont tangents au cercle circonscrit de centre Iint.
Le cercle de centre B passant par le centre Ia passe par les centres Ib et Ic. On cherche à le faire passer aussi par A et C.

Un triangle équilatéral très particulier : quand les cercles circonscrits passent par les centres des autres cercles circonscrits

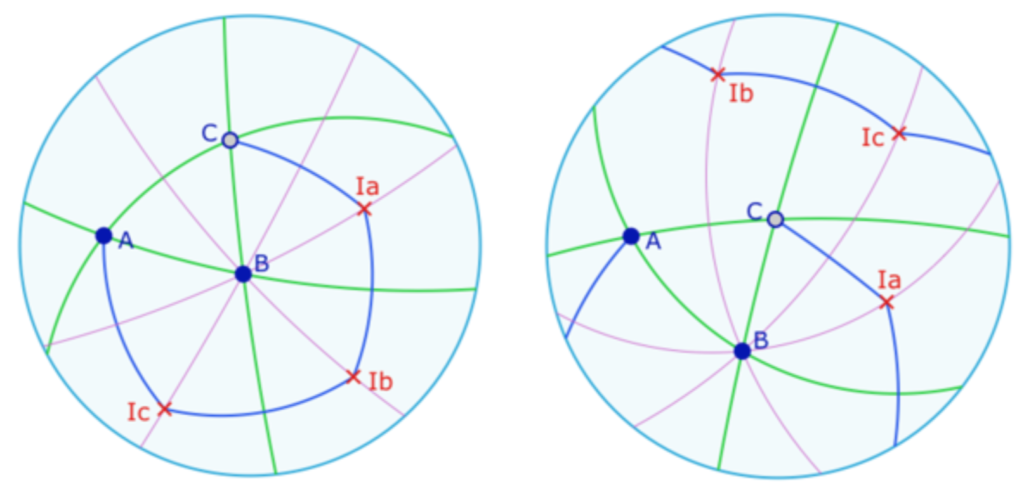
Dans la figure précédente, on arrive à faire passer le cercle de centre B passant par Ia par les points A et C en déplaçant le point B. Dans ce cas tous les centres Ix sont sur les cercles circonscrits extérieurs. Pour que cette configuration soit réalisable, il faut qu’avec le triangle initial, ces points soient les sommets d’un pentagone régulier. Et donc que le triangle initial soit un triangle équilatéral avec un angle de 72°.

Si l’angle serait facile à construire, ce qui importe, c’est de construire le côté associé.

Un peu de trigonométrie sphérique

Pour cela, il faut connaitre un peu de trigonométrie de la géométrie elliptique, c’est-à-dire de géométrie sphérique, les formules sont les mêmes. Deux formules sont utiles ici. On note a l’angle en le sommet A, opposé au côté [BC]. On note BC la distance elliptique de B à C (et pas seulement la longueur comme sur la sphère).

La « loi des cosinus » : \(cos BC = sin AB. sin AC . cos a + cos AB.cos AC\)

La formule des sinus : \(\displaystyle \frac{sin a}{sin BC}=\frac{sin b}{sin AC}=\frac{sin c}{sin AB}\)

Par un triangle équilatéral d’angle \(a=\displaystyle \frac{2\pi}{6}\), il vient \(cos BC = \displaystyle \frac{1}{\sqrt{5}}\) et \(sin BC = \displaystyle \frac{2}{\sqrt{5}}\), soit \(AB = BC = AC = tan^{-1}(2)\)

Chaque cercle circonscrit de centre Ia, Ib, Ic passe par les deux autres centres et est aussi de rayon atan(2).

Cette figure avait été le premier pentagone régulier elliptique. Voir les autres polygones réguliers des pages elliptiques : le changement de rotation de l’animation quand un arc de cercle change d’orientation est tout à fait intéressant à observer en terme de rapport entre modèle et interface …