Après avoir proposé , dans un précédent article, un environnement adapté à la réalisation de figures sur la pseudosphère de manière intrinsèque, nous proposons ici un environnement qui intègre, en plus, l’utilisation de la conjugaison avec le modèle de Klein-Beltrami.
La façon dont cet article est rédigé suppose – pour une construction effective des figures – que le lecteur soit déjà familiarisé avec les macros, et qu’il ait déjà réalisé quelques figures de l’article précédent (pour la pratique de la pseudosphère) et de l’article sur les macros de KB, ou encore celui traitant des figures sur la PSH car nous allons reprendre une partie des méthodes utilisées.
Les sections de l’article
• Présentation du contexte
• Les macros de la figure de base
• Bissectrices et cercle inscrit d’un triangle
• Les cercles exinscrits (suite de la précédente)
• Le cercle circonscrit partiel ou l’équidistante partielle
• Trilatère sur la pseudosphère
• Du modèle hyperbolique KB au modèle projectif KH
Présentation du contexte
et des choix retenus
Dans la présentation de la conjugaison, nous avions discuté du choix de paramétrisation de la longitude sur la feuille principale. Par exemple dans l’article sur les constructions intrinsèques, la feuille principale de la pseudosphère est paramétrée sur \([0, 2\pi[\). Or on a vu que, compte tenu de la projection de Beltrami, on a une bien meilleure lisibilité de la conjugaison avec KB, si la feuille principale est paramétrée sur \([-\pi, \pi[\). Pour une approche « pédagogique », nous avions alors proposé des figures permettant un choix entre les deux paramétrisations. Mais après une présentation initiale de découverte, cette démarche n’est plus pertinente, et artificiellement lourde. Dans cet article, nous retenons uniquement la paramétrisation sur \([-\pi, \pi[\).
Par rapport à l’article précédent, il suffit de modifier à la marge les macros de dessin (il n’y a qu’une ligne à modifier par point retourné). En pratique, les macros des figures de cet article ne sont donc pas exactement les mêmes que celles de l’article sur les macros intrinsèques.
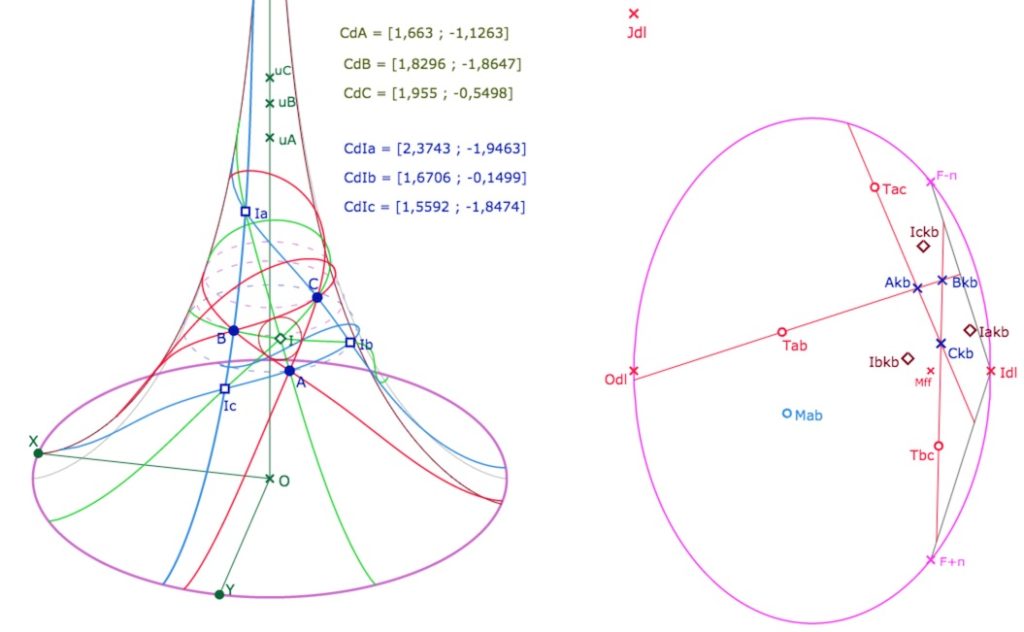
Principe de conjugaison – Horicycle image de la pseudosphère dans KB
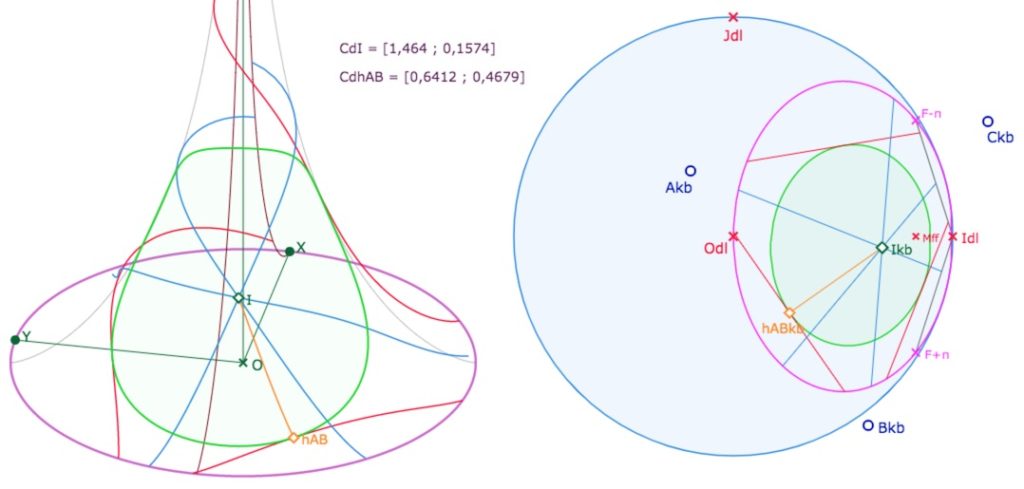
En une illustration, rappelons les principes généraux de la conjugaison entre les deux modèles, et son intérêt. Des points en manipulation directe sur la pseudosphère, ici \(A, B, C\), sont envoyés sur le « disque limite » de Beltrami – le modèle hyperbolique KB – en \(A_{kb}, B_{kb}, C_{kb}\). Les médiatrices sont tracées, à la fois sur la pseudosphère (de manière intrinsèque) et dans KB. Comme KB est un modèle de tout le plan hyperbolique on peut construire le cercle circonscrit, de centre \(o_{kb}\) qui n’est pas sur la pseudosphère – limitée à l’ellipse rose. On peut alors envoyer sur la pseudosphère (lieu rouge) la partie du cercle circonscrit au triangle \(ABC\) qui est sur la pseudosphère, ce qui ne serait pas possible de manière intrinsèque puisque le centre du cercle n’est pas sur la surface. Nous proposerons de faire cette figure au cours de cet article.
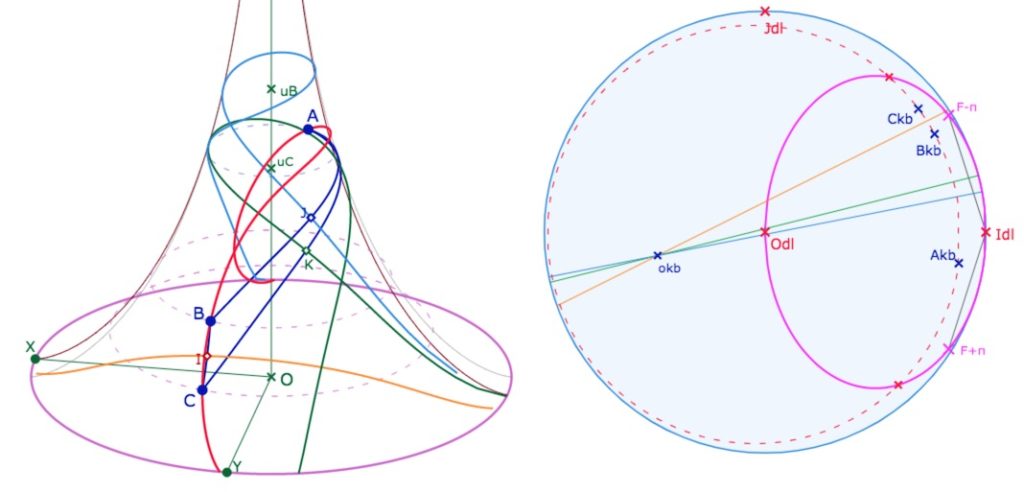
L’image de la pseudosphère par la projection de Beltrami – construite pour envoyer les géodésiques de la surface sur des droites euclidiennes – est l’ellipse rose qui, pour KB, est un horicyle de centre \(I_{dl}\), l’unique point à l’infini accessible à la pseudosphère.
La feuille principale de la pseudosphère (qui part du méridien passant par \(X\)) s’étend, dans le disque, du méridien issu de \(F_{-\pi}\) à celui passant par \(F_{+\pi}\).
Une macro « droite de la feuille principale pour la PS » dans KB.
Comme on l’a fait pour les deux autres modèles pseudosphériques, (ici pour la PSH et là pour la PSE), avant de présenter les macros de transfert, il peut-être intéressant de réaliser une macro « droite de la feuille principale pour la PS » dans KB, même si c’est moins essentiel cette fois, puisque l’on peut toujours construire les droites sur la PS depuis ses constantes (alors calculées depuis KB).
Comme pour les deux autres modèles il faut construire un segment dans une région précise. Il y a 4 points possibles d’intersection de la droite \((A_{kb}B_{kb})\) avec
• soit l’horicycle image de l’équateur : ce sont les points \(fh_1\) et \(fh_2\),
• soit le méridien \([F_{-\pi}O_{dl}]\) : le point \(fm\),
• soit le méridien \([F_{+\pi}O_{dl}]\) : le point \(fp\).
On illustre la programmation du choix des extrémités de la feuille principale avec une version en Blokckly – juste pour voir les imbrications conditionnelles – et la version en JavaScript qui peut être transformée en macro.
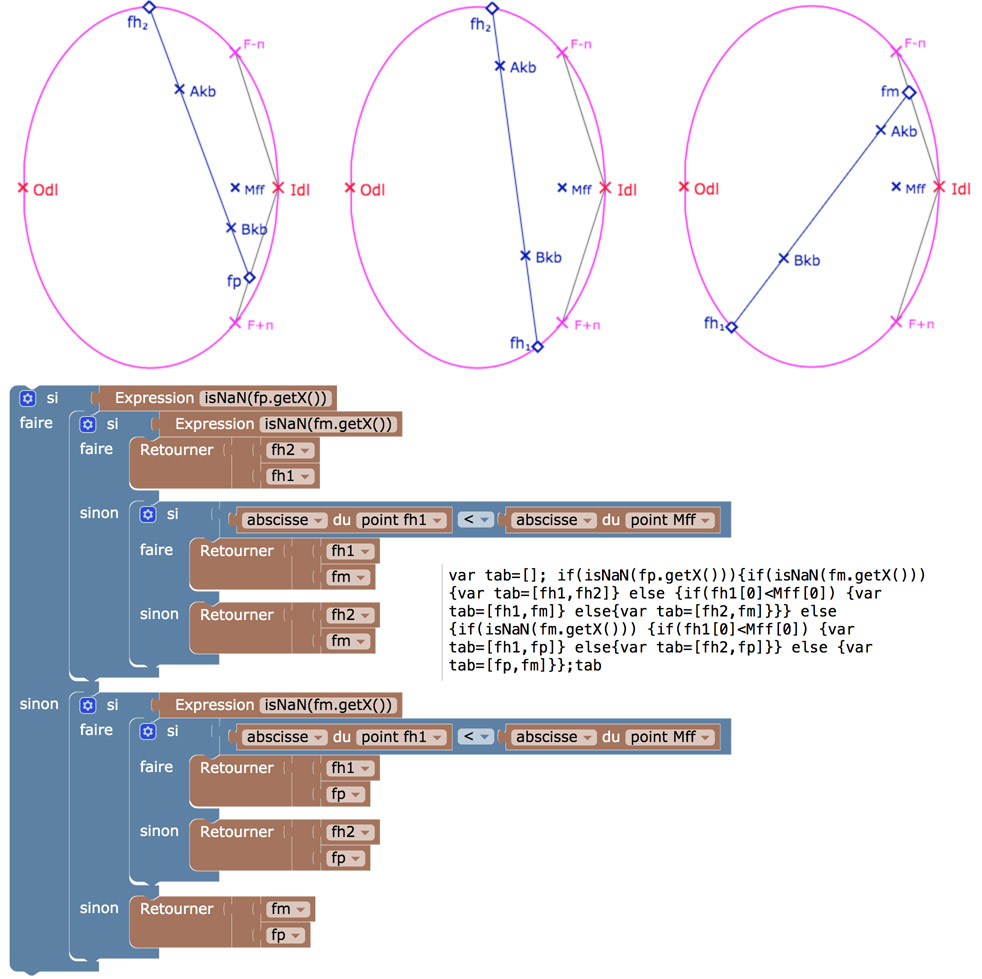
Application de la macro illustrée dans le tout dernier cas : d’un côté de la frontière de la feuille principale à l’autre côté.
Les macros embarquées
par la figure initiale
On a choisi de proposer à la fois l’essentiel des macros intrinsèques du premier article sur ce sujet, ainsi qu’une grande partie des macros KB comme déjà organisées pour les constructions sur la PSH, et bien entendu quelques macros de transfert. Il est peu probable que vous utilisiez toutes ces macros, mais globalement, cette double entrée « géométrie intrinsèque / conjugaison » autorise beaucoup plus de souplesse dans les choix que chacun peut faire pour ses constructions.
Lancer la figure initiale dans un nouvel onglet
Le premier niveau des dossiers et le contenu des dossiers sur KB
Dans l’illustration suivante, tout d’abord, à gauche, les six dossiers de premier niveau, trois sur KB, et trois sur la PS et le transfert entre les deux, puis au centre et à droite, l’intérieur des trois dossiers KB repris ou simplifiés de l’utilisation sur PSH. Le seul ajout est la macro construite ci-dessus placée en KBdroites 6. On détaillera son utilisation plus loin.
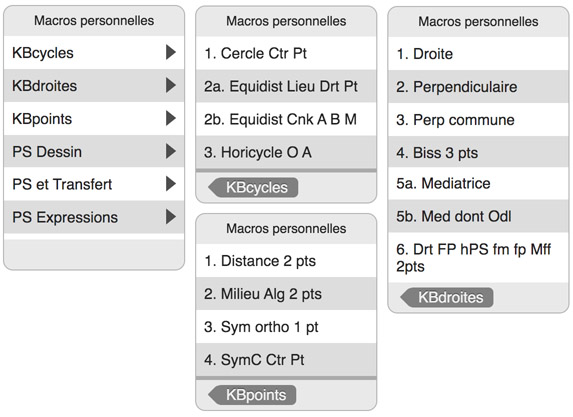
On rappelle que dans toutes les macros de KB (sauf la nouvelle KBdroites 6) on montre le cercle limite de Beltrami, et que cela efface le centre du cercle \(O_{dl}\). Il faudra le rendre à nouveau visible (outil gomme) pour utiliser les macros de transfert de KB vers PS.
Voici les macros des trois autres dossiers. Les dossiers PS Dessins et PS Expressions sont la reprise des mêmes de l’article précédent sur les constructions intrinsèques sur la pseudosphère.
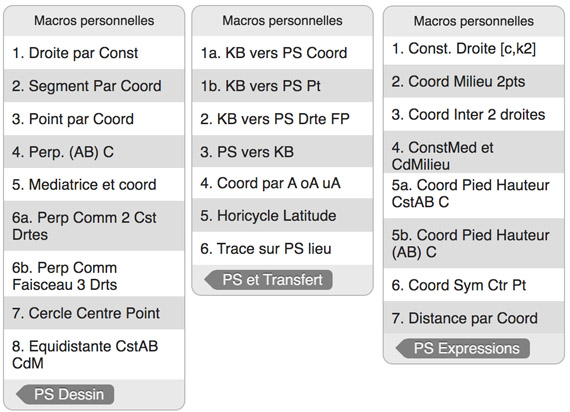
Le dossier PS et Transfert contient 6 macros. Il est organisé pour que l’on voit dans son écran d’ouverture, les quatre macros de transfert, les premières que l’on aura à utiliser.
Les macros de KB vers PS, que l’on nommera dans la suite Transfert 1a, Transfert 1b et Transfert 2 ont toutes les quatre mêmes objets initiaux : dans l’ordre les trois points \(O_{dl}, I_{dl}\) et \(J_{dl}\), puis un point \(M_{kb}\) que l’on veut transférer.
• Transfert 1a renvoie les coordonnées beltramiennes du point sans le construire. Cela peut être utile pour calculer soit les constantes d’une droite, soit dessiner un cercle.
• Transfert 1b renvoie les coordonnées d’un point et le construit aussi sur la surface. On a toujours besoin des coordonnées d’un point de la surface si on veut le réutiliser par la suite.
• Transfert 2 construit le lieu du point sur la surface. Cela suppose que le point \(M_{kb}\) est le point d’un segment ou d’une droite – typiquement d’une droite de la feuille principale.
On pourrait être surpris de ces objets initiaux, car dans l’utilisation des macros de la PSH (ce serait pareil pour la PSE), on n’a besoin que du centre \(O_{dl}\). Cela vient du fait qu’ici on peut agrandir le cercle de Beltrami pour avoir la partie de projection (l’ellipse rose) assez grande, alors que dans les deux autres modèle le cercle est toujours un cercle unité. On aurait pu, par contre, se passer de \(J_{dl}\) en modifiant la macro.
La macro Transfert 3 (PS vers KB) s’applique à un point de la surface. Elle a pour objets initiaux les coordonnées de ce point, et les deux points \(O_{dl}, I_{dl}\). Elle a été utilisée pour construire les trois points \(A_{kb}, B_{kb}, C_{kb}\). Elle pourrait être utilisée, éventuellement pour des vérifications par exemple.
Le second écran de ce dossier contient deux macros d’archive et une macro qui sera effectivement utilisée. Tout d’abord les macros de construction de points sur la pseudosphère – que l’on notera PS 4 et PS 5 ce ne sont pas des « transfert » – sur les coordonnées d’un point et la construction d’un « cercle horicycle ». On y a ajouté la macro utilisée dans la dernière figure de l’article précédent, pour tracer des horicycles, que l’on a renommé Trace sur PS lieu que l’on référencera Transfert 6 : elle construit un lieu sur la pseudosphère depuis un point du plan, en désignant deux points (et pas leurs coordonnées) le point sur la PS et l’antécédent de cette « fonction lieu » très générale. En pratique on l’appliquera pour les traces de cercles ou d’équidistante sur la PS quand des éléments constituant sont en dehors de la surface comme dans l’illustration d’introduction.
Une première figure :
le cercle inscrit du triangle
Lancer la figure initiale dans un nouvel onglet
Pour ce qui est des droites remarquables d’un triangle, dans les macros intrinsèques, il manque les bissectrices, c’est donc par cela que l’on va commencer.
Étape 1 – deux bissectrices dans KB
On construit deux bissectrices (3 sommets du triangle et le cercle limite), puis leur intersection \(I_{kb}\), centre du cercle inscrit. Pour cette intersection, on se place en mode standard (flèche gauche sélectionnée) et on utilise l’interface du logiciel : en cliquant sur l’intersection des deux (les deux segments doivent être surlignés), la palette contextuelle des points apparait et on choisit l’icone « point » en haut à droite de la palette pour créer l’intersection.
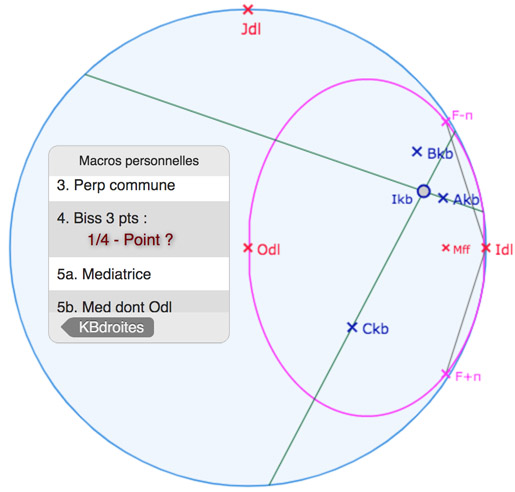
Les bissectrices sont des droites KB. On les cache (outil gomme) et on va construire leurs traces sur la feuille principale.
Étape 2 : les bissectrices sur la feuille principale dans KB
On commence par construire les droites restreintes à la feuille principale en utilisant deux de ses points, ici un sommet du triangle et le centre du cercle inscrit de la façon suivante :
Utilisation de la macro KBdroites 6 : Drte FP hPS fm fp Mff 2 pts
On montre dans l’ordre, l’horicycle de la pseudosphère (rose) hPS, les deux méridiens limites de la feuille principale fm (celui du haut, frontière moins \(\pi\)) et fp (du bas, frontière plus \(\pi\)), puis le milieu de leurs extrémités, le point Mff, et enfin les deux points de la droite à construire, comme \(C_{kb}\) et \(I_{kb}\). On applique cela trois fois, pour les trois bissectrices.
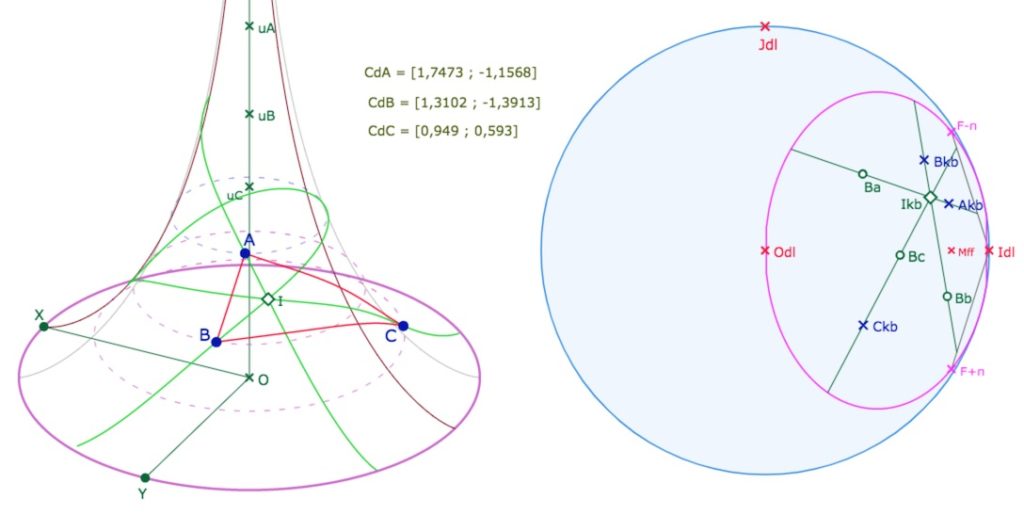
Étape 3 : retour sur la pseudosphère
Il suffit ensuite de prendre un point sur chacune de ces droites, ce sont les points \(B_a, B_b\) et \(B_c\), et appliquer, trois fois, la macro Transfert 2 (KB vers PS Drte FP), ce qui construit les trois bissectrice, sur la feuille principale.
Dans l’illustration précédente, on a aussi appliqué Transfert 1b (KB vers PS Pt) qui place le centre du cercle inscrit sur la pseudosphère.
Etape 4 : ajouter le cercle inscrit
Avec les macros dont on dispose, il y a deux façons de finaliser le cercle inscrit. On a besoin des coordonnée du centre et d’un point du cercle. En effet, sauf si on a envie de voir la construction dans KB, on évitera de le construire dans KB car la construction n’est pas nécessaire et nécessite une quarantaine d’objets. On a déjà dessiné le centre du cercle. On utilise Transfert 1a pour avoir les coordonnées du centre, nommé CdI dans l’illustration suivante.
Pour le point du cercle on peut le construire dans KB ou simplement calculer ses coordonnées sur la pseudosphère.
Version 1 : construction dans KB
• On commence par construit la perpendiculaire à \((B_{kb}C_{kb})\) issue de \(I_{kb}\). On utilise à nouveau la macro Transfert 1a qui donne les coordonnées du point, que l’on renomme par exemple CdhBC
• Ensuite on construit le cercle sur la pseudosphère par la macro PS Dessin 7 (Cercle Centre Point).
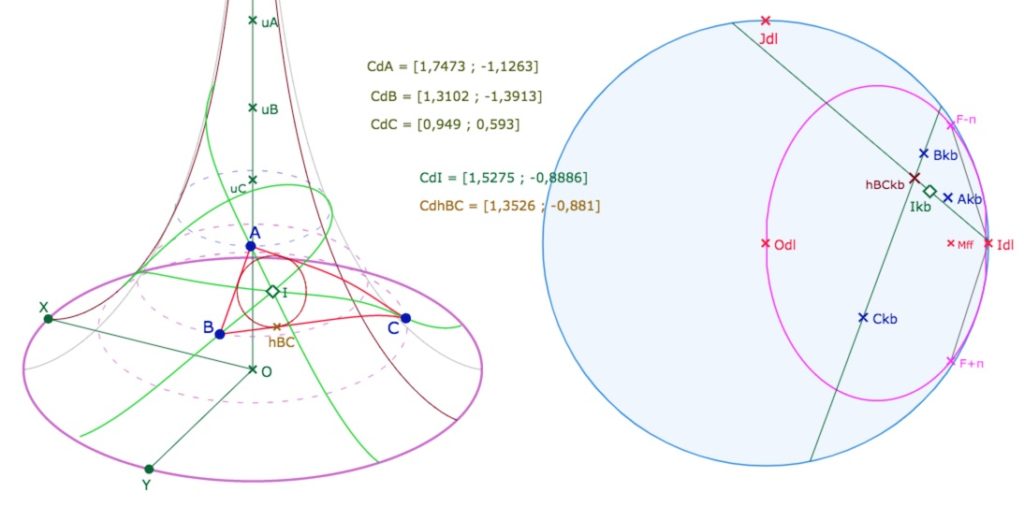
Sur cette illustration, on a ajouté le point \(hBC\) mais ce n’est pas nécessaire pour la construction. Pour ce point, on a utilisé la macro PS Dessin 3 (Point par Coordonnées).
Remarque technique : la formulation « que l’on renomme par exemple CdhBC » est possiblement ambigüe car il peut y avoir confusion entre le nom de la variable et le commentaire texte de l’expression. Ceci a été détaillé et commenté dans l’article précédent (section « Utilisation des items de base »). En général quand il n’y a qu’un terme, sans espace, il est préférable de renommer la variable (donc avec l’inspecteur d’objet) plutôt que de modifier le commentaire (avec l’outil calculatrice). De toute façon, le logiciel n’utilise en interne que le nom de la variable.
Version 2 : calcul direct sur la surface (plus rapide et utilise moins d’objets)
On peut calculer les coordonnées du projeté orthogonal du centre du cercle inscrit sur un des côtés du triangle avec PS Expressions 5b en montrant les coordonnées (par exemple) de \(B, C\) et \(I\). On obtient une expression dont le commentaire est Coord Hc. On termine comme dans la version 1, avec PS Dessin 7 (il n’est pas nécessaire de modifier le commentaire)
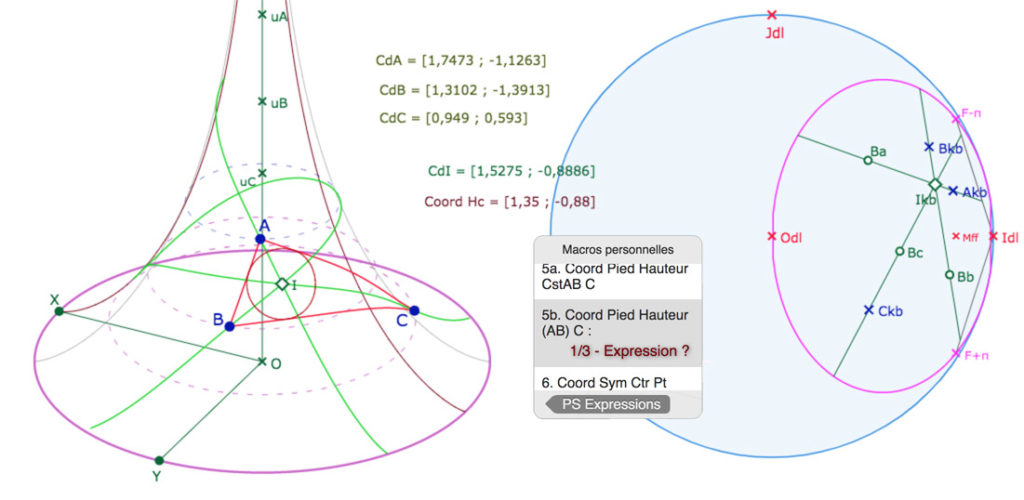
Avant de poursuivre, si on le souhaite, on peut enregistrer cette première figure. La méthode d’enregistrement a été présentée dans la toute première section de l’article précédent sur les macros de la PS.
Poursuite de la figure :
les cercles exinscrits
D’un point de vue constructif, il n’y a réellement que deux nouvelles droites à construire dans KB pour obtenir les informations permettant de construire les trois cercles exinscrits et les bissectrices extérieures. Bien entendu, pour finaliser la figure on sera amené à en construire bien d’autres, en particulier avec KBdroites 6 autour de la feuille principale. Mais techniquement la construction reste simple, c’est essentiellement un enchaînement de macros des dossiers PS Transfert et PS Expressions. Ce qui prend du temps c’est de la rendre la plus lisible possible.
Étape 1 : placement des points sur la surface – première droite de KB
Dans un premier temps, il faut toutefois se placer dans une configuration où les cercles exinscrits vont bien être entièrement sur la surface. C’est en fait le seul point sur lequel il faut être attentif, le reste se déroule quasiment tout seul. Pour cela on peut placer les latitudes des sommets, et les sommets, dans une configuration proche de celle-ci à gauche : les latitudes sont plus hautes que dans l’illustration précédente.
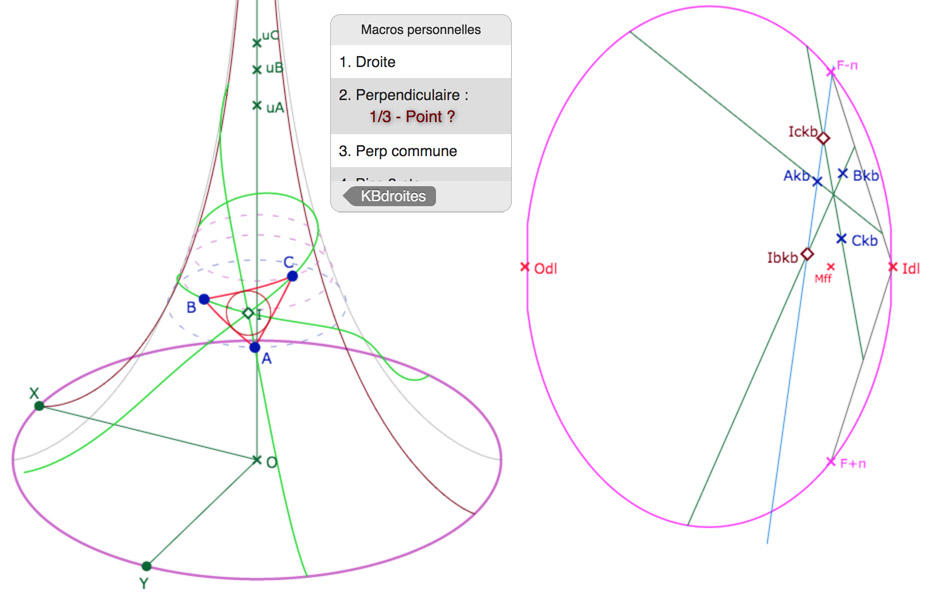
Dans l’illustration de droite, on a construit la première droite avec KBdroites 2, la perpendiculaire à la bissectrice du sommet \(A_{kb}\), issue de ce point. (droite bleue ci-dessus qui dépasse l’horicycle rose car c’est une droite limitée par le cercle de Beltrami – qu’il faut montrer pour appliquer la macro. Cette droite coupe les deux autres bissectrices en les deux centres de cercles exinscrits \(Ic_{kb}\) et \(Ib_{kb}\).
Étape 2 – Les bissectrices extérieures sur KB et PS, les trois centres des cercles
2a. Les bissectrices dans KB
Désormais on utilise la macro KBdroites 6 : Drte FP hPS fm fp Mff 2 pts, dont les objets initiaux ont été détaillés à l’étape 2 de la section précédente.
• Tout d’abord avec les points \(Ic_{kb}\) et \(B_{kb}\) : c’est la bissectrice extérieure passant par \(B_{kb}\), ce qui permet de construire le troisième centre de cercle exinscrit \(Ia_{kb}\). (Illustration de gauche).
• On peut ensuite cacher les trois première bissectrices intérieures (elles sont déjà tracées sur la pseudosphère). On applique à nouveau deux fois KBdroites 6 avec les centres des cercles exinscrits.
Sur l’illustration de droite, on a déjà placé trois points sur les bissectrices pour la construction sur la surface avec Transfert 2.
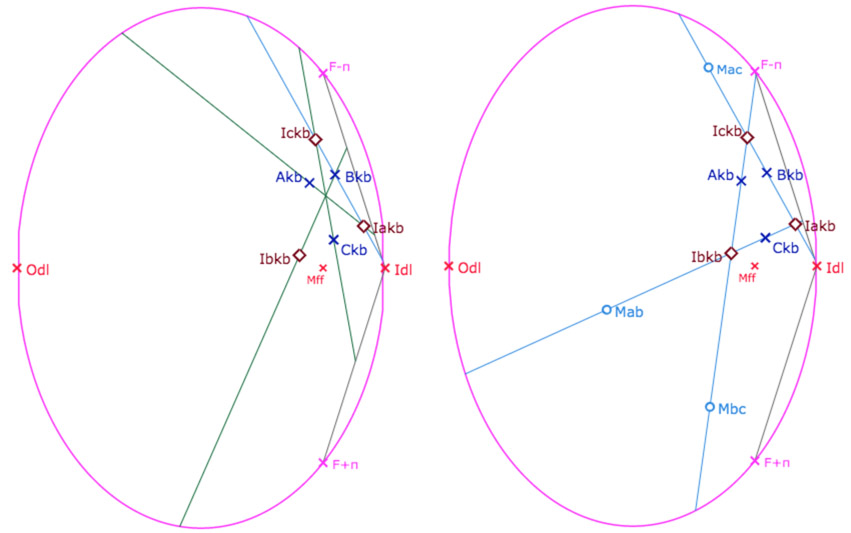
2b. Passage sur la pseudosphère, centre des cercles exinscrits
Dans l’illustration suivante, on a donc
• d’abord utilisé trois fois la macro Transfert 2 (KB vers PS Drte FP) sur les points \(M_{ab}, M_{bc}, M_{ac}\),
• ensuite, on utilise la macro Transfert 1a (KB vers PS Coord) sur les centres des cercles exinscrits. Dans l’illustration, on a renommé les noms des variables coordonnées (inspecteur d’objets).
• enfin, la macro PS Dessin 3 pour construire les centres des cercles exinscrits sur la surface.
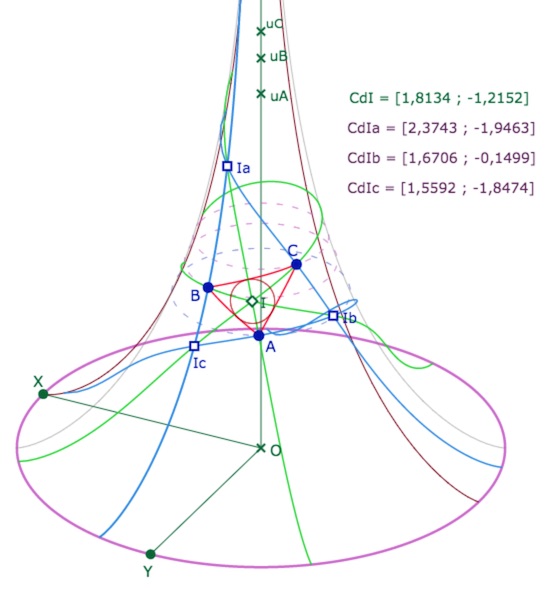
Les trois bissectrices extérieures, en bleu clair, et les trois centres des cercles exinscrits
Étape 3 – Tracer les droites (limitées à la feuille principale) du triangle
Avant de construire les cercles, pour voir qu’il sont bien tangents aux côtés, il faut tracer les droites passant par les sommets du triangle. On pourrait le faire avec les macros intrinsèques mais on n’a pas retenu la macro « Feuille principale intrinsèque » donc on va utiliser à nouveau KBdroites 6, sinon, avec les droites multifeuilles, la figures peut facilement devenir assez illisible.
• Commencer par supprimer les lieux « segments côtés du triangle » sur la pseudophère.
• On peut cacher les KB-bissectrices extérieures avant de poursuivre, pour plus de lisibilité.
• Utiliser à nouveau trois fois KBdroites 6 aux sommets du triangle pris deux à deux et poser des points, sur ces droites, ci dessous, \(T_{ab}\), \(T_{bc}\) et \(T_{ac}\).
• Puis Transfert 2 (KB vers PS Drte FP) sur chacun des points \(T_{ab}, T_{bc}\) et \(T_{ac}\). Cela donne :
Étape 4 – Finalisation de la figure
Il reste à déterminer un point de chacun des cercles exinscrits. Pour préparer une étape supplémentaire, on choisit de calculer les projections des trois centres exinscrits tous sur la même droite \((AB)\).
• On applique donc la macro PS Expressions 5b (projection orthogonale d’un point sur une droite) aux points \(A\) et \(B\) et à chaque centre \(I_a, I_b, I_c\) successivement. Dans l’illustration, on a modifié le commentaire produit (mode expression, icone calculatrice), mais on peut ne pas le faire, en plaçant chaque commentaire à côté du centre concerné par exemple.
• Puis on applique enfin la macro de tracé de cercle PS Dessin 7.
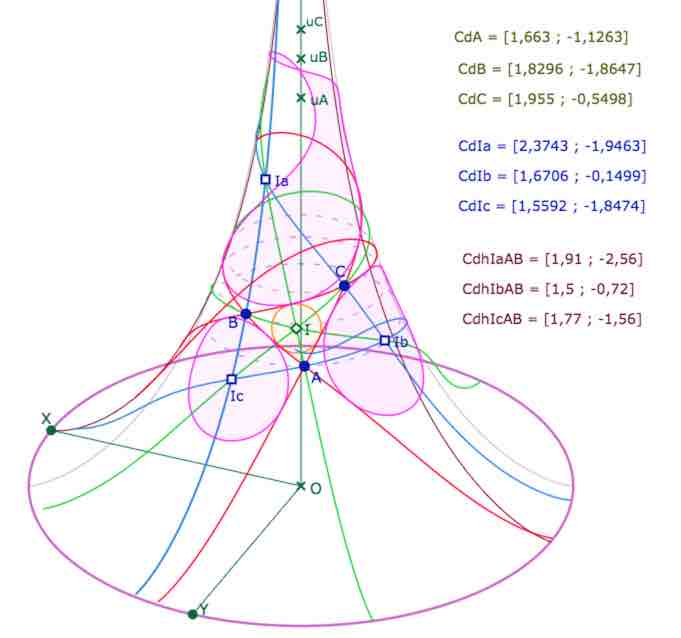
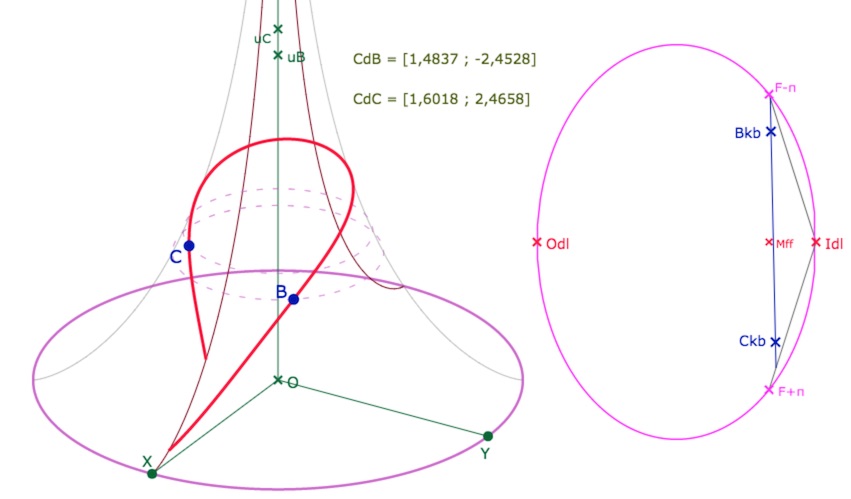
On voit que l’on a été prudent. On peut abaisser la latitude \(u_A\), largement, ce qui rapproche le centre \(I_a\) de la feuille précédent la feuille principale (se voit clairement sur KB) et donc fait du cercle exinscrit un cercle multifeuille (au moins sur trois feuilles) :
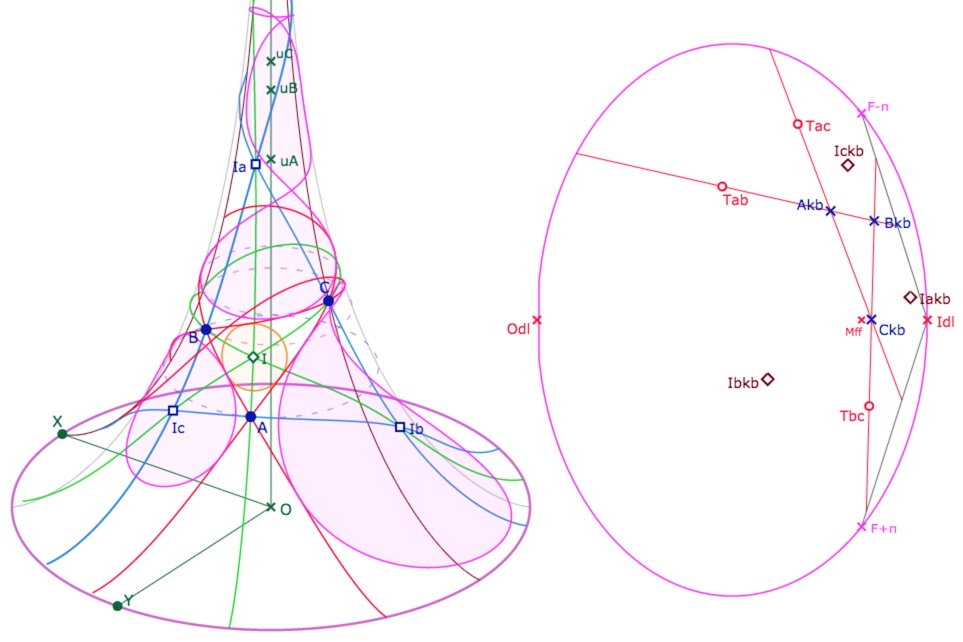
Vue de dessus de la même configuration
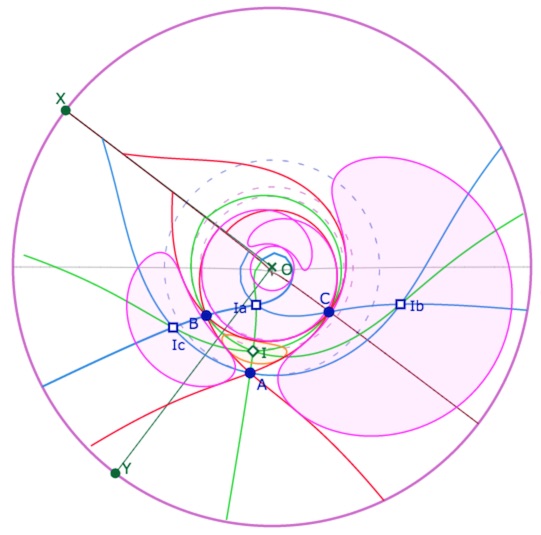
Complément sur une propriété métrique
Cette propriété a déjà été mentionné dans cet article sur les macros de KB. On se propose de la vérifier à nouveau sur la pseudosphère. On peut juste lire le résultat ci-dessous, ou faire ces derniers calculs
La propriété : le milieu \(K\) de \(A\) et \(B\), est aussi le milieu des projections sur \((AB)\) des centres \(Ia\) et \(Ib\) ainsi que le milieu des projection orthogonales de \(Ic\) et \(I\).
Pour réaliser ce complément sur la figure, il faut :
• calculer les coordonnées de \(K\) milieu de \(A\) et \(B\) ; macro PS Expressions 2
• calculer les coordonnées de la projection orthogonale du centre du cercle inscrit sur \((AB)\) : macro PS Expressions 5b appliquées à \(A, B\) et \(CdI\) (expression produite dans l’étape 4 de la section précédente).
• calculer les distances (PS Expressions 7) \(d(K,hIAB)\) et \(d(K,hIcAB)\), puis \(d(K,hIaAB)\) et \(d(H,hIbAB)\). Ci-dessous, les calculs de distance sont illustrés à 7 décimales.

Traces sur la PS du cercle
ou de l’équidistante
circonscrite à un triangle
Dans cette section on regarde comment construire, sur la pseudosphère, la partie d’un cercle ou d’une équidistante circonscrite à un triangle, en particulier quand le centre du cercle ou la perpendiculaire commune aux médiatrices ne sont pas sur la pseudosphère, et donc que les calculs intrinsèques ne s’appliquent pas.
Pour aller à l’essentiel on a choisi de vous proposer une figure déjà avancée, car il n’est pas nécessaire de refaire ce qui a été fait dans les sections précédentes.
Lancer la figure Médiatrice de base illustrée ci-dessous
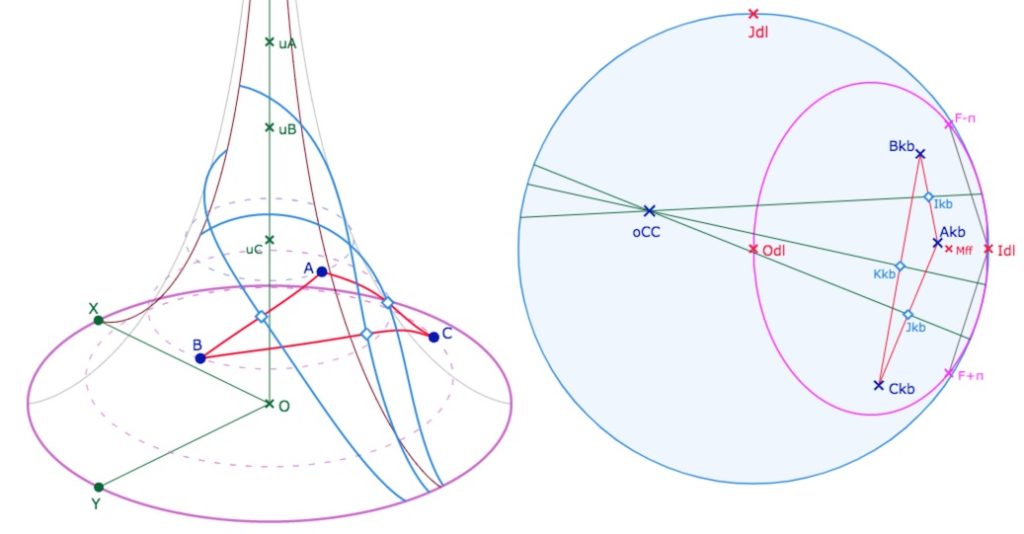
On a construit les médiatrices « entières » dans KB, mais pour plus de lisibilité, sur la pseudosphère, on a gardé leurs traces seulement sur la feuille principale, avec les macros usuelles comme KBdroites 6.
Etape 1 – Trace sur la pseudosphère du cercle circonscrit au triangle
Il n’est pas nécessaire de nommer les points comme cela est fait dans la suite : ils sont nommés ici juste pour communiquer avec plus de précision.
• Construire le cercle circonscrit dans KB avec la macro KBCycles 1
• Dans l’environnement standard de DGPad (flèche gauche active), construire les deux intersections des deux coniques \(u_{CC}\) et \(v_{CC}\), avec la palette contextuelle des intersections (s’approcher d’une intersection et quand les deux coniques sont surlignées, cliquer et choisir l’icone point en haut comme illustré ci-contre).
• Sur le segment \([u_{CC} \; v_{CC}] \) prendre un point nommé ci-dessous \(M_{ccir}\). La demi-droite de centre \(Odl\) passant par \(M_{ccir}\) coupe le cercle circonscrit au triangle en \(PtC_{kb}\).
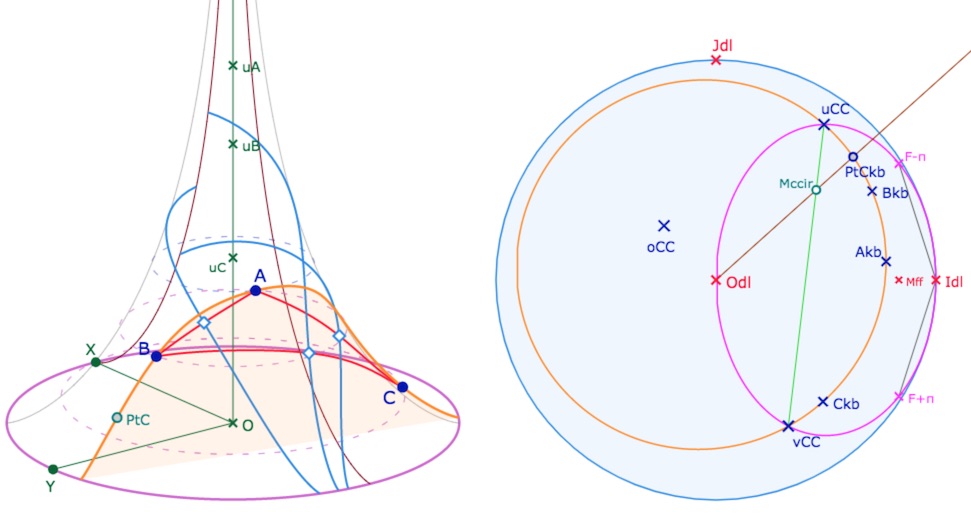
• Envoyer alors ce point sur la pseudosphère par la macro PS et Transfert 1b : KB vers PS Pt : on construit le point nommé ci-dessus \(PtC\).
• Terminer par la macro PS et Transfert 6 : Trace sur PS Lieu. On montre d’abord ce point \(PtC\) puis le point \(M_{ccir}\).
Ci dessus on a choisi de colorier (opacité à 0.1) ce lieu, mais cela n’est pas nécessaire et peu induire parfois en erreur.
Étape 2 – Même démarche pour le cas de l’équidistante.
Se placer dans le cas où les médiatrices ne sont pas concourantes. Il suffit de descendre \(u_A\) par exemple.
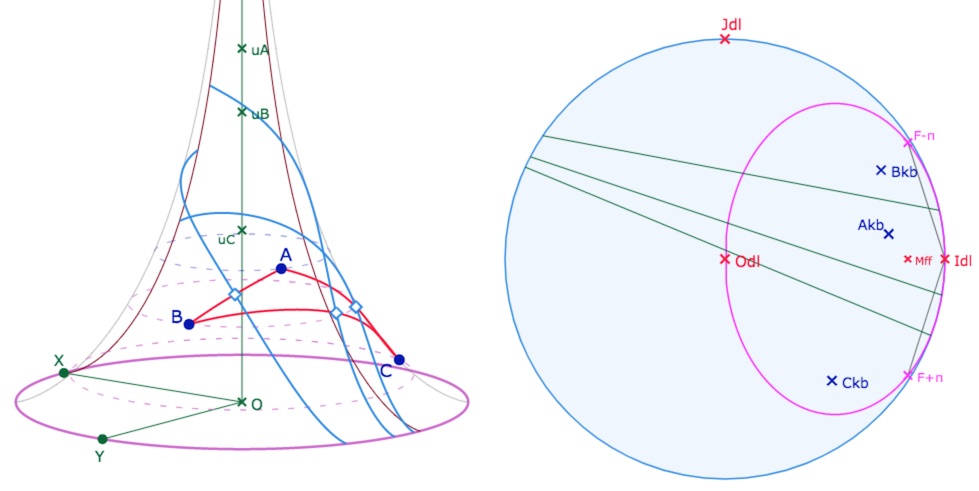
• Commencer par construire la perpendiculaire commune aux médiatrices par KBdroites 3.
• Pour pouvoir appliquer la macro suivante, il faut créer deux points d’intersection entre la perpendiculaire commune et deux médiatrices. (dans la prochaine illustration, nommés \(H_1 \) et \(H_2 \), mais il n’est pas nécessaire de les nommer).
• Appliquer alors la macro KBCycles 2b : Equidist Cnk AB M à ces deux points et un sommet, par exemple \(A_{kb}\).
• Comme dans le cas du cercle circonscrit, construire les deux intersections des deux coniques, ci-dessous nommées \(u_{Eq}\) et \(v_{Eq}\).
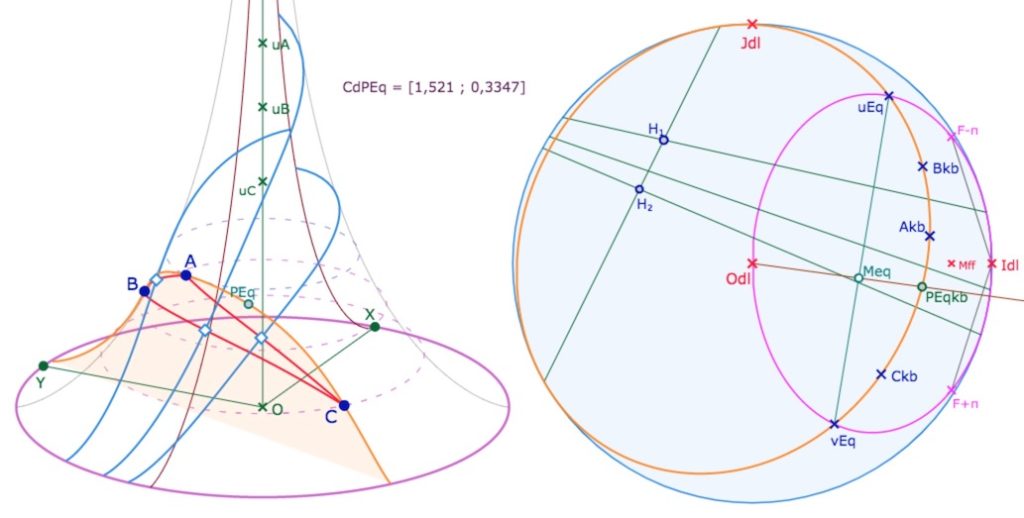
• Sur le segment \([u_{Eq} \; v_{Eq}] \) prendre un point nommé ci-dessous \(M_{eq}\). La demi-droite de centre \(Odl\) passant par \(M_{eq}\) coupe le cercle circonscrit au triangle en \(PEq_{kb}\).
• On termine comme ci-dessus, avec la macro PS et Transfert 1b qui construit sur la pseudosphère le point \(PEq\), et enfin le lieu de ce point quand \(M_{eq}\) décrit le segment entre les deux intersections, par la macro PS et Transfert 6.
Chacun comprend bien que l’on fait deux fois la même construction, une fois pour le cercle, quand les médiatrices sont concourantes et une autre fois pour l’équidistante quand elles ont une perpendiculaire commune. On a expliqué (dans le menu DP) en quoi ces deux aspects sont distincts puisque l’on a deux types de faisceaux de droites différents. Pour cette construction, on aurait pourtant envie qu’ils relèvent d’un seul point de vue, pour réaliser une seule construction. Le lecteur averti aura reconnu cet autre point de vue, les autres le découvriront dans la dernière section de cet article.
Étape 3 – Affiner (éventuellement) cette construction
L’intersection de deux coniques contient, dans le cas général, 4 points. Quand il n’y a que deux points, comme ici – mais aussi comme on l’a bien détaillé aussi dans le modèle non arguésien de Hilbert, ces deux points peuvent dynamiquement ne pas rester les mêmes. On ne va pas résoudre la question comme présenté dans le cas de Hilbert, car il faudrait entrer dans le code des macros, on peut simplement refaire la figure dans ce cas là (quand la perpendiculaire commune rentre dans l’horicycle de la pseudosphère) :
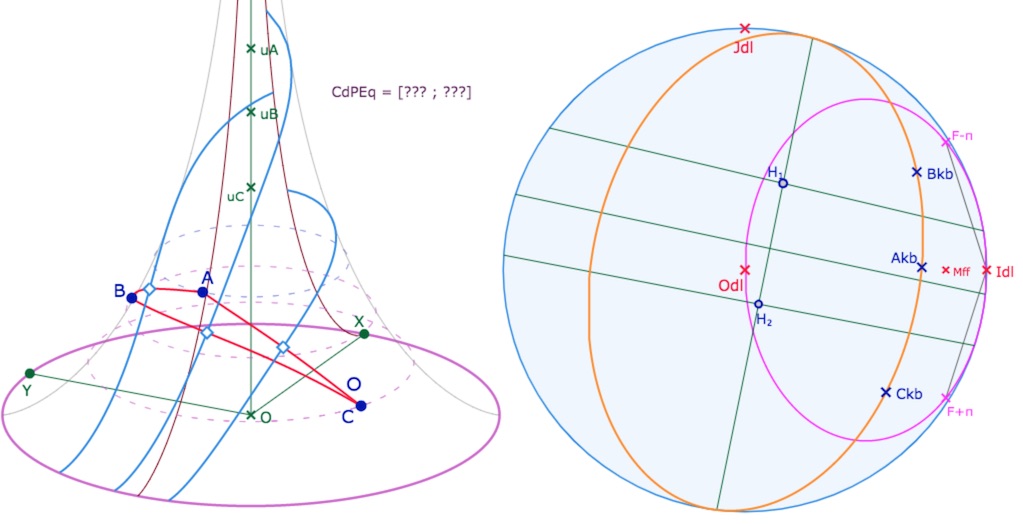
Dans cette configuration les deux intersections des coniques ne sont plus \(u_{Eq}\) et \(v_{Eq}\), mais les deux autres, ici encore non nommées, qu’il faut construire pour poursuivre la figure.
Il y a des solutions simples, pour éviter de refaire l’étape précédente, mais demanderait d’entrer un peu plus dans le fonctionnement du logiciel, par exemple par la construction de macros, ou encore de rendre les points d’intersection booléens comme fait dans le modèle non arguésien de Hilbert. Ce que l’on a choisi de ne pas développer (pour le moment).
Remarque : le changement d’intersection ne se produit pas avec le cercle. On peut raisonnablement penser qu’ici cela apparaît car la perpendiculaire commune – de par sa construction – change d’orientation quand elle franchit le centre du cercle.
Trilatère sur la pseudosphère
On termine cet article par deux propositions de constructions sur les trilatères … en free-style, et le complément culturel annoncé à la section sur les cycles circonscrits. On propose au lecteur cette nouvelle figure de base … assez minimaliste.
:
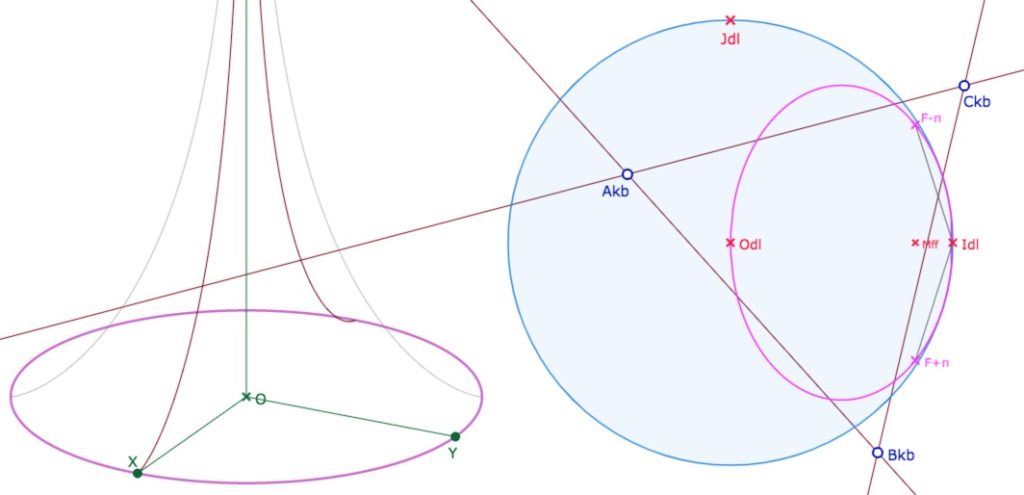
Lancer cette nouvelle figure de base (dans un nouvel onglet).
Les trois points \(A_{kb}, B_{kb}, C_{kb}\) sont pris dans le prolongement projectif du modèle KB (en pratique, dans le plan usuel, on y reviendra dans la dernière section). Il faut bien-sûr que les droites coupent l’horicycle limite de la pseudosphère pour que les trilatères existent sur la pseudosphère.
Fonctionnement des points de base du trilatère
Les trois points \(A_{kb}, B_{kb}, C_{kb}\) sont des points dit « flottants » c’est-à-dire qu’ils ne sont pas liés au repère 3D : ils ne changent pas de place quand la pseudosphère tourne par exemple. C’est bien entendu le cas aussi du centre \(O_{dl}\) du cercle de KB. Un point est rendu flottant avec l’icone « punaise » de la palette de comportement sous le point.
Comme ces quatre points sont flottants cela signifie aussi qu’ils sont indépendants les uns des autres : si on déplace \(O_{dl}\) toute la construction dans le cercle se déplace mais avec les trois points \(A_{kb}, B_{kb}, C_{kb}\), eux, immobiles. Il faut donc y penser … et si possible éviter de déplacer le point \(O_{dl}\) : il vaut mieux déplacer le centre du repère 3D, origine de la pseudosphère.
Construction générique préalable
• On commencera par construire la trace des droites sur la feuille principale selon la méthode déjà détaillée plus haut.
• Éventuellement enregistrer cette figure pour la relancer ensuite pour passer à une nouvelle construction.
Première figure proposée : les hauteurs et le cercle inscrit du triangle orthique
Pour prendre une KB-perpendiculaire, utiliser plutôt les droites usuelles préalables (marron) que leurs traces à l’intérieur de l’horicycle rose.

Le trilatère rouge, ses hauteurs bleues, le triangle orthique vert et son cercle inscrit de centre l’orthocentre
Bien entendu, on peut faire entrer les trois points \(A_{kb}, B_{kb}, C_{kb}\) sur la pseudosphère.
Deuxième figure proposée ; le cercle inscrit d’un trilatère
Pour conserver les premières droites du trilatère sur la pseudosphère, on peut simplement supprimer les hauteurs dans KB, ou encore ouvrir la figure partielle dans un autre onglet avec DGPad, si elle a été enregistrée. Pour les bissectrices, il suffit de les prendre avec KBdroites 4 sur les sommets \(A_{kb}, B_{kb}, C_{kb}\). Il est assez rapide de finaliser la figure suivante. Le cercle sur la pseudosphère est construit de manière intrinsèque (KBcycles 1) par ses coordonnées obtenues par PS et Transfert 1b. KB vers PS Pt.
Du modèle hyperbolique KB au modèle projectif KH
La section précédente sur les trilatères est l’occasion pour proposer l’élargissement conceptuel suivant.
Réflexions sur une figure fausse issue de l’application d’une macro
Au tout début de cet article sur les troncatures de pavages dans KB, on a présenté la macro algébrique KB–milieu de deux points, utilisée ici. En fait il suffit qu’une droite définie par deux points coupe le cercle-limite de Beltrami pour qu’elle puisse s’appliquer. Il s’agit bien du milieu hyperbolique des deux points quand ils sont tous les deux à l’intérieur du cercle, mais cette construction a-t-elle un sens quand les deux points sont à l’extérieur du modèle KB, ou encore quand un est à l’intérieur et l’autre à l’extérieur ? On peut déjà simplement explorer la situation sur le triangle \(A_{kb}B_{kb}C_{kb}\).
Relancer la figure de base des trilatère (dans un nouvel onglet) pour faire ceci

• à gauche, avec un point à l’intérieur et un autre à l’extérieur, les éventuelles médianes ne sont pas concourantes, ce qui n’a rien de surprenant : le symétrique de \(A_{kb}\) par rapport à \(K\) est un point à l’intérieur du cercle, donc ne peut pas être \(C_{kb}\) : ce point \(K\) ne peux pas être milieu des deux sommets du triangle.
• à droite, la situation est plus troublante, si les trois points sont extérieurs au triangle, les droites « candidates-médianes » sont toujours concourantes. Cela-a-t-il un sens mathématique ?
Présentation succincte du modèle KH
Cette situation a déjà été abordée, à l’intérieur de ce site s’entend, dans cette présentation des modèles projectifs KE-KH largement étudiés par Daniel Perrin. (KE pour Klein Elliptique et KH pour Klein Hyperbolique). KH est un plongement projectif du modèle hyperbolique KB. C’est d’abord un plan projectif, et ce n’est pas un modèle hyperbolique … il y a même des questions d’incidence.
Si vous n’aviez pas entendu parlé de l’approche – novatrice, d’une grande rigueur et tellement efficace – que fait Daniel Perrin des géométries non euclidiennes, un petit détour vers cet article sera, certes assez dépaysant, mais aussi des plus rafraichissants. Dans la suite, on résume en quelques ligne la situation rencontrée ici.
Dans KH, par la nature même des objets, le milieu de deux points existe seulement si ces deux points sont intérieurs au cercle, ou s’ils sont tous les deux extérieurs. L’orthogonalité dans KH (comme KE) est issue d’une forme quadratique. Il en résulte, entre autres, parmi de nombreux résultats que
• deux points ont toujours deux milieux.
• la polaire de l’un des milieux est une médiatrice de ces deux points passant par l’autre milieu.
Dans KH les médianes d’un triangle dont les trois points sont tous intérieurs ou extérieurs au cercle sont concourantes. Reste cette question : pourquoi les calculs faits a priori dans le contexte de la distance au sens de Cayley dans KB donnent les mêmes milieux que dans KH ? Daniel Perrin a largement abordé cette question, avec ses propres invariants (la géométrie étant l’étude des groupes opérant sur des invariants). Toujours dans curvica974, un autre article traite de la question de la distance dans KE et KH. Et, on y illustre comment Daniel Perrin, avec son invariant, retrouve bien les formules de Cayley dans KB . Ainsi notre macro KBpoints 2. Milieu Alg 2 pts fourni bien un milieu de deux points, au sens de KH, quand les deux points sont extérieurs au cercle.
Réaliser quelques figures dans KH et sur la PS
On propose au lecteur de jouer un peu avec quelques macros de KH dans une figure adaptée.
Lancer la nouvelle figure PS_Conjug_Trilatere_KH dans un nouvel onglet dont voici les nouvelles macros dans le dossier KH.

• Pour toutes les macros de KH on montre d’abord le cercle de Beltrami. Pour voir les deux milieux de deux points, diminuer significativement le rayon du cercle.
• KH 4 est en réalité l’invariant de Daniel Perrin. Ce n’est qu’une première étape avant la distance. On verra qu’il peut prendre des valeurs négatives. Se référer à l’article sur les distances de KE et KH pour plus de précision.
• On rappelle que quand une macro utilise un cercle (ici toutes les macros), alors le centre \(O_{dl}\) du cercle est caché. On le retrouve avec l’icone « gomme ».
• Par défaut les milieux sont nommés \(I_{kh}\), affinement entre les deux points \(J_{kh}\), à l’extérieur. On les a renommés respectivement \(I_{1}\) et \(I_{2}\).
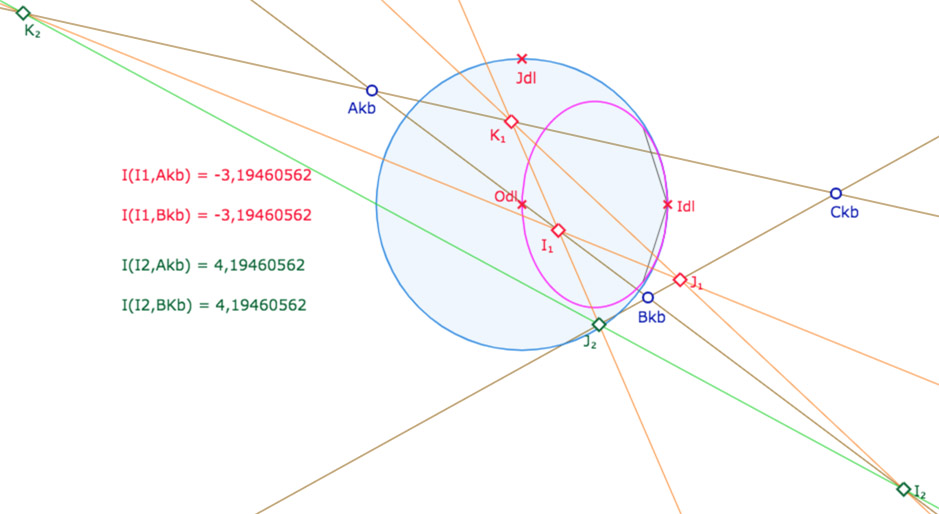
KH n’est pas un modèle hyperbolique : ci-dessus les 4 droites des milieux d’un triangle.
On ajouté les valeurs rendues par l’invariant sur la droite \((A_{kh}B_{kh})\).
On notera que \(d(I_1, A_{kb})+d(I_2, A_{kb})=1\).
Tester aussi la valeur de \(d(I_1, I_2)\) … ce n’est pas un bug, voir l’article.
Figure réalisable : les (vraies) médianes d’un trilatère
On utilise les mêmes méthodes que dans les figures précédentes.
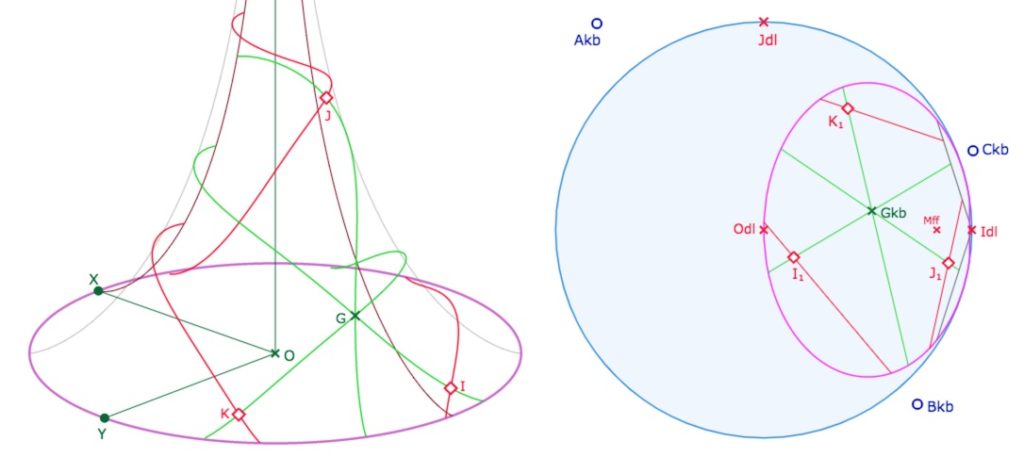
En rouge les droites du trilatère, en vert les médianes du trilatère.
Ici seuls les milieux sont construits avec KH, le reste est réalisé avec les macros usuelles.
Hauteurs d’un trilatère et le cycle exinscrit du triangle orthique associé
On a commencé les constructions sur les trilatères avec les hauteurs et le cercle inscrit du triangle orthique associé. On poursuit avec une configuration où le cycle tritangent au triangle orthique est soit un cercle, inscrit ou exinscrit, soit une équidistante exinscrite.
Pour conserver les droites rouges de la figure précédente il suffit de supprimer les milieux indicés 1.
On peut aussi reprendre la figure depuis le début en lançant à nouveau PS_Conjug_Trilatere_KH dans un nouvel onglet.
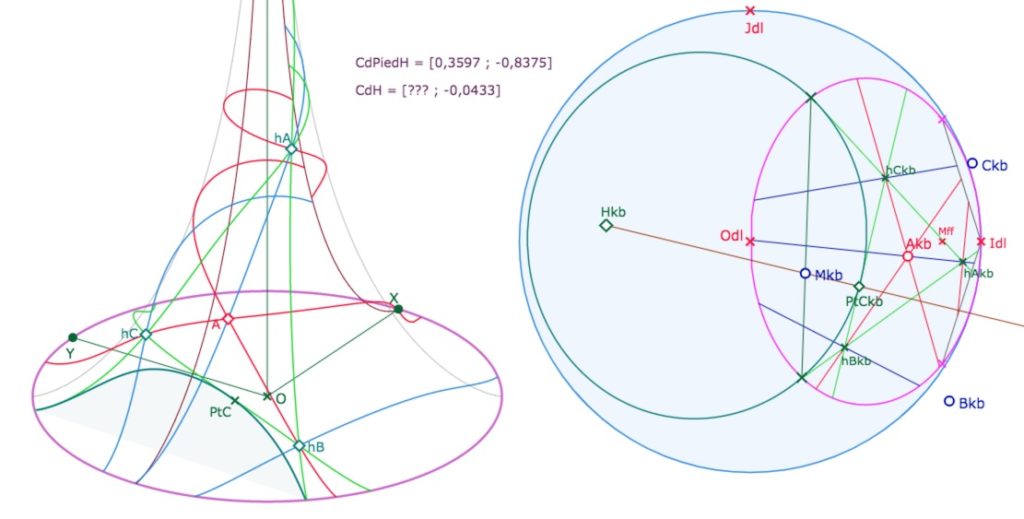
Ci-dessus, les droites sont toujours en rouge, les hauteurs sont bleues, le triangle orthique en vert clair et le cercle exinscrit, de centre \(H_{kb}\) dans KB, en cyan. Il est construit comme le cercle circonscrit dans une section précédente, c’est le lieu (par PS et Transfert 6) de \(PtC\) en fonction de \(M_{kb}\).
L’intérêt de ce point de vue projectif est que l’on a en même temps la construction du cercle exinscrit et de l’équidistante exinscrite : car \(H_{kb}\) est soit le centre du cercle soit le pôle de l’équidistante : cette équidistante est toujours, pour KH, un cercle de centre \(H_{kb}\).
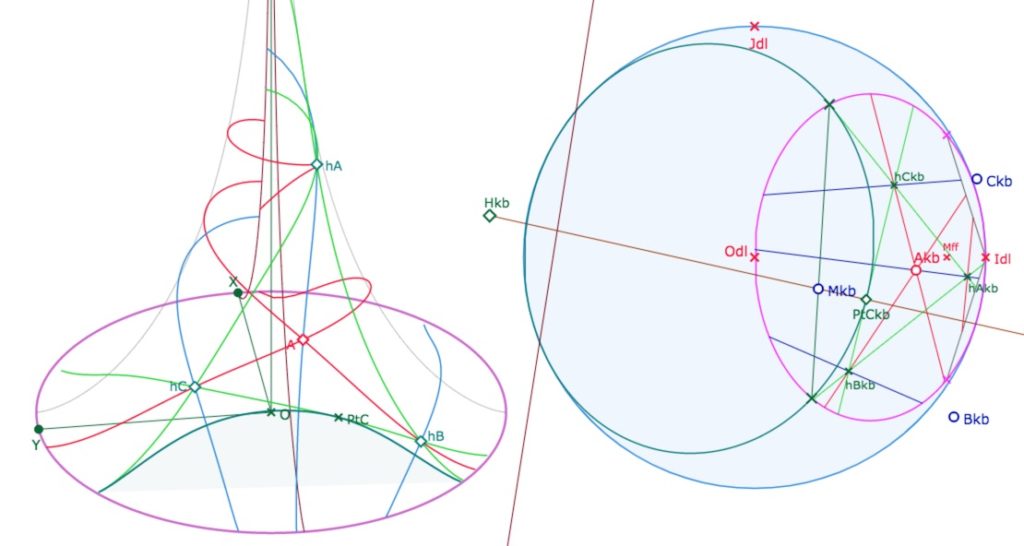
Quand \(H_{kb}\) est en dehors du cercle, sa polaire est la perpendiculaire commune aux hauteurs. Le cercle de centre \(H_{kb}\) (dans l’environnement KH) est bitangent au cercle c’est alors aussi une équidistante pour KB.
Plus de précisions sur les cercles de KE et KH dans cet autre article. En particulier on y explique pourquoi l’équidistante peut prendre une forme différente quand le triangle orthique devient lui-même un trilatère comme ci-dessous.
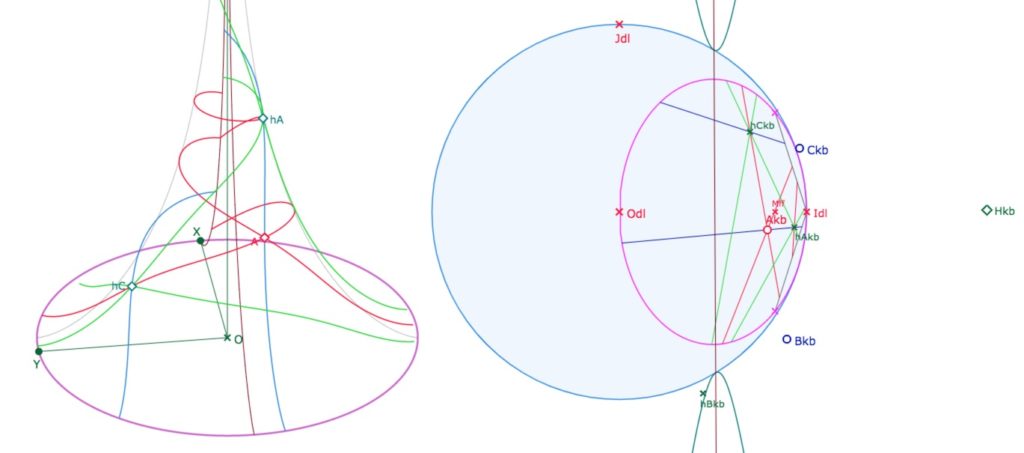
Quand le pied d’une hauteur devient lui aussi extérieur au cercle, le cycle associé est alors entièrement extérieure au cercle – et donc n’a aucune trace sur la pseudosphère. Le cycle est tangent au cercle de Beltrami en les deux points de contact de la polaire de \(H_{kb}\) comme dans le cas usuel de KB ci-dessus.
Bien entendu, le point \(H\) peut aussi être le centre d’un cercle exinscrit du triangle orthique entièrement inscrit dans la pseudosphère comme ici :
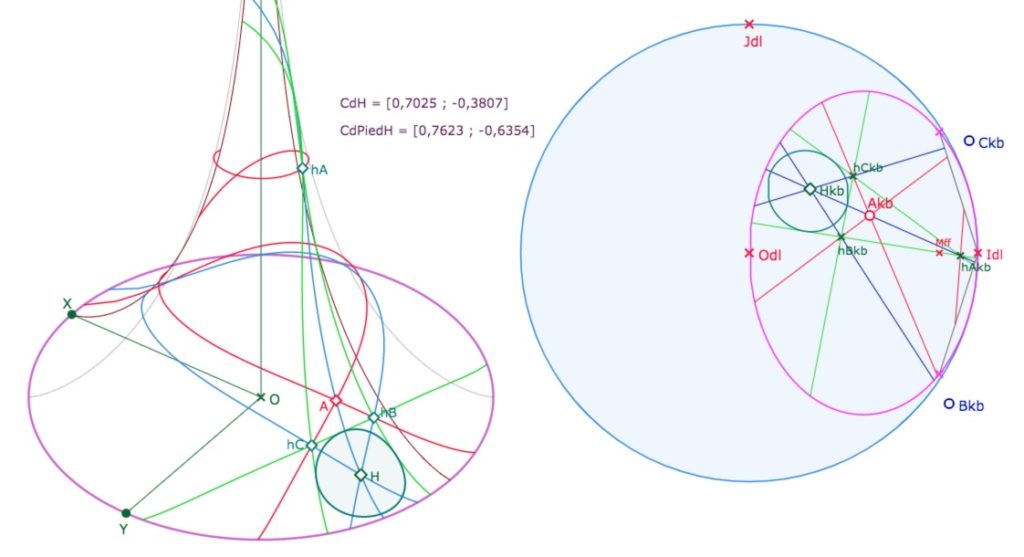
Mais il faut faire une construction supplémentaire, car les deux coniques de KB ne se coupant pas les points \(M_{kb}\) et \(PtC_{kb}\) n’existent plus. On voit que l’on a
• renvoyé les coordonnées de l’orthocentre et de l’une de ses projections sur un côté du triangle par PS et Transfert 1a puis
• utilisé la macro PS Dessin 7. Et alors cette construction fonctionne aussi quand l’orthocentre est à l’intérieur du triangle orthique et que le cercle devient ainsi le cercle inscrit.
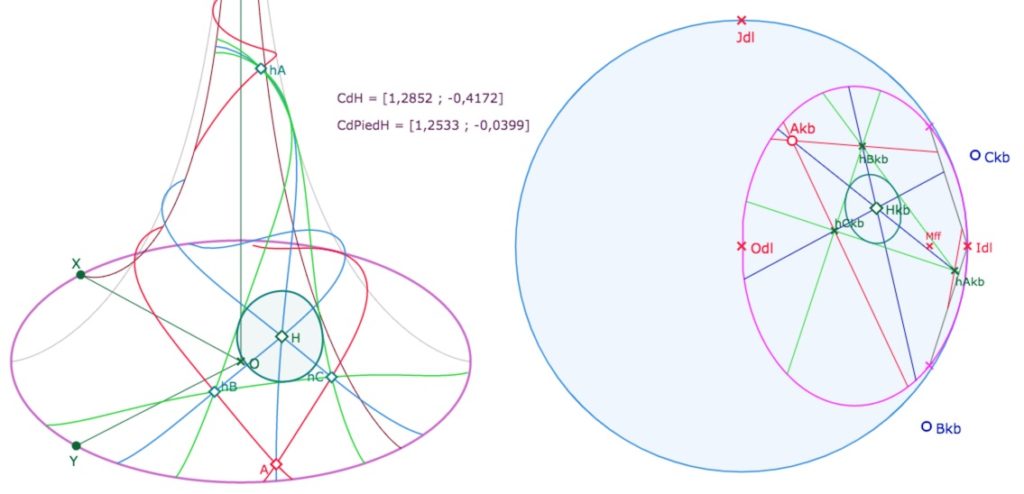
Il y a tant à explorer encore, mais on a choisi d’arrêter l’article ici.
Rappel des trois articles actuellement disponibles sur le site concernant les modèles projectifs KE et KH.
Les modèles projectifs KE et KH – 1 – les droites
KEKH – 2a – Les cercles (introduction)
KE KH – 3 – Longueur, distance et angles
Spécial lecteurs qui ont moins de temps
Même si l’esprit de l’article est d’apprendre à faire ces figures, on peut être intéressé sans avoir vraiment envie – ou simplement le temps – de faire tout cela. Alors voici, aussi, les figures faites dans ce site, avec une ou deux figures de travail, non reprises dans l’article.
Il faut dézipper le fichier et glisser les figures sur l’application en ligne https://www.dgpad.net/