Cet article est une présentation rapide des macros du modèle de géométrie hyperbolique du modèle de Klein-Beltrami (KB) comme il a été présenté dans cette page. C’est aussi l’occasion de présenter un résultat métrique – absolu – sur les cycles exinscrits d’un triangle. Cet ensemble de macro est utilisé pour les figures par conjugaison avec la pseudosphère (PS) et, toujours, avec la pseudosphère hyperbolique (PSH). D’autres pages proposeront ce types d’utilisation.
Reprendre la page de présentation de l’utilisation des macros de DGPad.
Les macros de KB
Comme les objets, en dehors du cercle limite, sont des points ou des segments, il n’y a aucune ambiguïté sur la demande « cercle », c’est toujours le cercle limite de Beltrami, celui dans lequel on fait la figure. Dans les macros KB – contrairement aux macros dans le disque de Poincaré (menu DP) ou le disque de Klein (menu ELL), le cercle horizon est le dernier objet à montrer dans les macros.
On rappelles que l’usage d’un cercle dans une macro – donc toujours ici – cache le centre de ce cercle. Ce n’est pas important ici, car le centre n’est utilisé que dans la macro KB Med dont Odl qui sert essentiellement pour reproduire des angles et en particulier dans les pavages – un article spécifique sera consacré à cette question.
Pour faire réapparaitre le cercle, activer l’outil gomme et sélectionner le centre du cercle Odl.
Classiquement, les macros sont regroupées en trois dossiers : Points, Droites et Cycles.
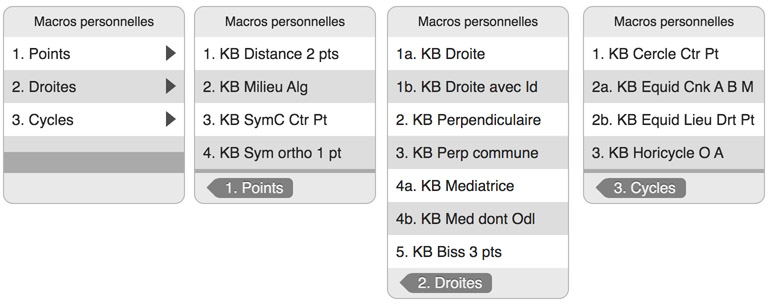
Le dossier « Points«
Les macros sont classiques. On consultera cette page sur les troncatures de pavages pour la présentation des macros algébriques Milieu et Symétrie Centrale.
Contrairement aux autres modèles hyperboliques ou elliptiques, il n’y a pas de macro intersection de deux droites car on utilise simplement l’outil usuel de DGPad d’intersection de deux segments : il faut donc être en mode standard, c’est-à-dire l’icone de gauche du tableau de bord activée.
A propos de la macro KB distance : par construction, la macro renvoie la distance certes, mais au même endroit. Si on veut l’appliquer plusieurs fois, il convient de déplacer le renvoi. Cela se fait pendant que l’on est en mode macro.
Par ailleurs, le nom de la variable associée à la distance, s’appelle \(dMN\) par défaut avec un suffixe. Par exemple, si on l’applique à trois points \(A, B, C\) cela donne : \(dMN, dMN0\), et \(dMN1\) qu’il convient ensuite de modifier dans le mode aspect des objets (icone « roue »).

Modification de dMN déjà effectuée, celle de dMN0 en cours
Le dossier « Droites »
Différence entre les deux macros KB droite : la première construit la droite hyperbolique passant par deux points (la corde du cercle en fait) et la seconde (avec Pt idéaux) ajoute les extrémités de la corde, ce sont les points à l’infini. Cela peut être utile dans certaines constructions.
Différence entre les deux macros KB médiatrice : il y a la macro générique, standard, pour laquelle on donne deux points et le cercle du modèle. Pour construire cette médiatrice, on utilise le pôle d’une droite. Or cette droite passe par un des deux points, ce qui n’est pas possible si un des points est le centre du cercle du modèle, car le pôle est à l’infini. C’est pour cela qu’il y a une seconde macro KB Med dont Odl qui construit la KB-médiatrice entre un point et le centre du cercle du modèle. Cette macro attend, d’abord le cercle du modèle, ensuite l’autre point que le centre du cercle.
Le dossier « Cycles »
Différence entre les deux macros KB équidistante : la première (Cnk A B M) rend une conique (Cnk) et demande trois points : A et B sont les points de l’axe de l’équidistante et M est le point par lequel passe l’équidistante. Cette première macro est plus esthétique au sens où elle trace toute la conique, mais ne correspond par à la définition de l’équidistante par image d’un point par les droites d’un faisceau. Elle correspond plutôt à une définition métrique : l’ensemble des points à même distance de la droite (AB) que le point M, et dans le modèle KB, donc ajoute la partie de la conique de l’autre côté de l’axe que le point M.
La seconde macro (Lieu Drt Pt) construit seulement le lieu attendu (une seule partie de la conique). Elle demande non plus deux points mais la KB-droite, l’axe de l’équidistante, et un point par lequel passe l’équidistante. Cette seconde macro est plus conforme à la définition de l’équidistante retenue dans ce site.
A propos de la macro KB Horicycle O A : cette macro attend un point situé sur le cercle (le centre de l’horicycle) et un autre point, appartenant à l’horicycle. Contrairement aux autres macros pour lesquelles les points attendus peuvent être créés pendant l’application de la macro, le point \(O\) doit, lui, être créé avant. Cela vient du fait que ce point appartient au cercle qui est lui-même demandé comme objet initial de la macro : c’est logiquement complexe à trancher comme situation.
La figure contenant toutes ces macros
Lancer (dans un nouvel onglet) la figure de base avec toutes ces macros KB.
Dans la suite quelques détails techniques – d’interface – sur des figures que l’on peut réaliser assez rapidement, puis une figure un peu plus sophistiquée qui illustre un résultat métrique absolu, c’est-à-dire vrai dans les contextes euclidien, elliptique ou hyperbolique.
Construire des points d’intersection – Exemple des médianes
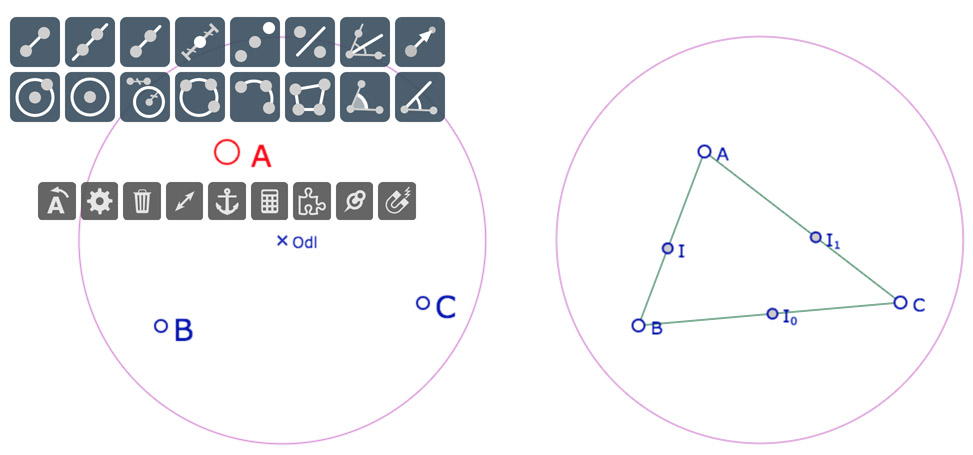
On veut construire les KB-milieux \(I, J, K\) du triangle \(ABC\). Pour cela on commence par construire les côtés du triangle, qui sont des segments euclidiens, en utilisant l’interface de construction du logiciel. Il faut être alors en mode standard, sélectionner un point (comme \(A\) ci-dessous) et, dans la palette contextuelle des points, sélectionner l’outil segment (icone la plus à gauche de l’illustration de gauche) et lâcher la souris – ou le doigt – sur un autre sommet.
Puis on utilise ensuite trois fois la macro KB Milieu Alg ce qui créé les milieux nommés automatiquement \(I, I_0, I_1\) comme l’illustration de droite.
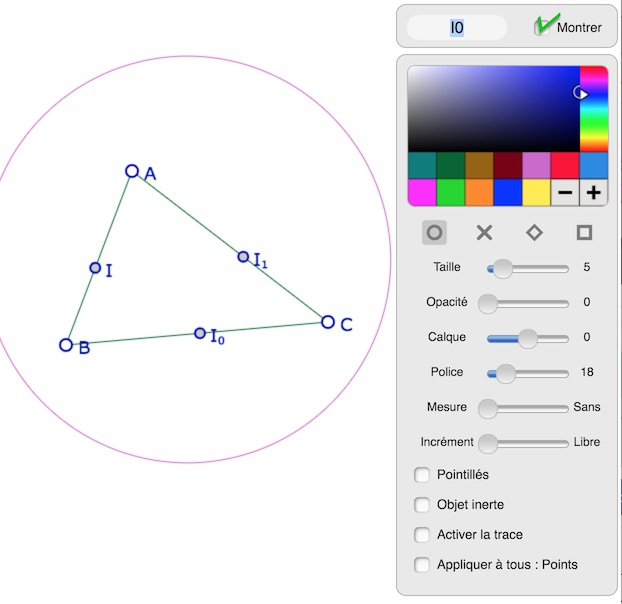
On passe alors en mode Inspecteur des objets (icone « roue » du tableau de bord) pour changer les noms des milieux.
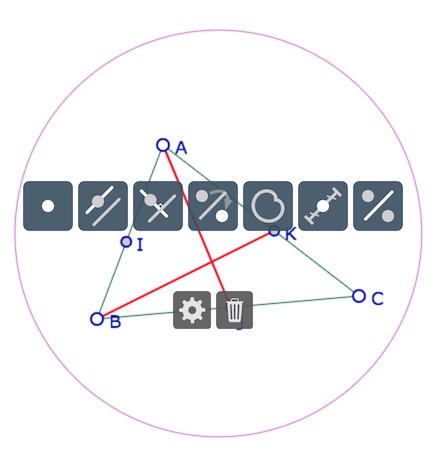
Pour les médianes – dont on sait qu’elles sont concourantes – on revient en mode standard, pour construire les médianes comme segment euclidien. Pour l’intersection, on la construit à partir de deux médianes. Pour cela, toujours en mode standard, on se rapproche de l’intersection de deux médianes jusqu’à ce qu’elle soient toutes les deux surlignées comme ci-dessous, et on choisi l’icone point à gauche de la palette.
Nommer des points – Cacher/Montrer des objets
Pour que les figures aient l’aspect des illustrations de ce site, il faut pratiquer un peu l’interface du logiciel comme déjà signalé plus haut. On nomme les points à partir du module aspect des objets (icone « roue »). Cacher ou montrer les objets se fait dans le mode « gomme« .
Exemple du cycle circonscrit
(cercle et équidistante)
Depuis trois points, on peut construire les droites ou les segments, puis les médiatrices. On aurait pu faire comme dans les macros DP, à savoir une macro de type Bachmann, à savoir une macro Cycle par pinceau et point, mais on ne l’a pas fait. Et donc il faut faire deux construction : si les méditrices sont concourantes, on construit le cercle circonscrit, sinon, on construit la perpendiculaire commune aux médiatrices et l’équidistante circonscrite.
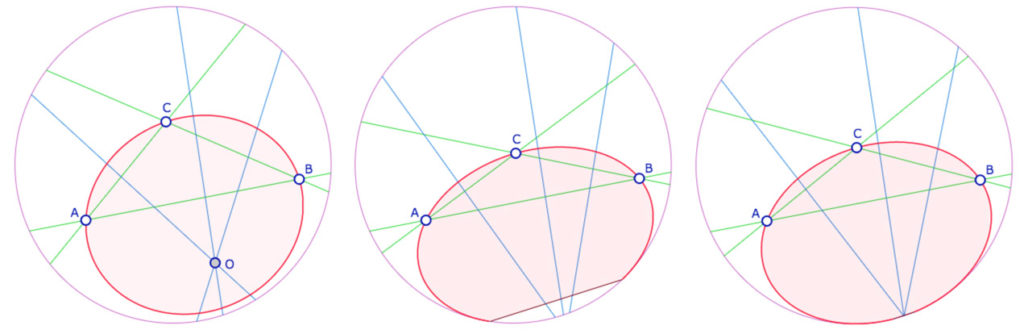
à gauche l’application de KB Cercle, au centre l’application de KB Equidist Lieu,
à droite, la même macro dans une situation proche de l’horicycle (on distingue la l’axe de l’équidistante)
Complément technique : comment obtenir un triangle ayant un horicycle circonscrit ?
En prenant trois points de base \(A, B, C,\) on ne peut pas atteindre (à la souris ou au doigt) le cas de l’horicycle.
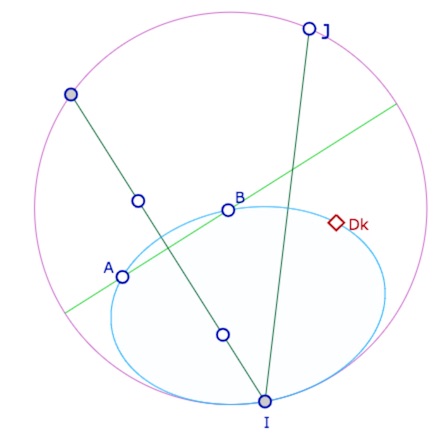
Pour construire un triangle avec un horicycle circonscrit, on choisit de construire \(C\) à partir de \(A\) et \(B\). Pour cela, il faut prendre un des points idéaux de la médiatrice de \(A\) et \(B\). Puis prendre une droite passant par ce point, et construire \(C\) comme symétrique de \(A\) ou \(B\) par rapport à cette droite.
Mais comment prendre un point idéal de la médiatrice de \(A\) et \(B\) ? Le plus simple reste de prendre deux points sur cette médiatrice et utiliser la macro Droite avec Pts idéaux (voir ci-contre) puis on termine la figure avec la macro Sym Ortho 1 pt qui donne le point \(D_k\) ci-contre.
La construction de l’horicycle de centre \(I\) passant par \(A\) passe bien par \(B\) et \(D_k\).
Remarque pratique : dans l’illustration précédente, et la figure ci-dessous, la conique représentant l’horicycle est de densité 1500, alors qu’elle n’est que de 500 par l’application de la macro. Si on voulait refaire cette figure, cela se règle dans l’inspecteur d’objet sur la conique.
Manipulation de la figure ainsi construite
On peut déplacer \(A, B\) ou J. On notera qu’en déplaçant \(J\) on voit \(C\) parcourir l’horicycle de centre \(I\) passant par \(JA/latex].
Illustration d’une propriété métrique absolue
Une autre utilisation des macros peut être la construction du cercle inscrit et des cercles exinscrits d’un triangle (on pourrait étendre au cycles exinscrits sans difficulté. C’est l’occasion de parler d’une propriété absolue sur les points de contact des cercles inscrits et exinscrits sur un côté du triangle (au sens large, sur la droite support).
Nous proposons au lecteur de faire la figure suivante. On se donne trois points [latex]A\), \(B\) et \(C\) , puis \(I\) le centre du cercle inscrit au triangle, \(K\) le milieu des points \(B\) et \(C\). Puis, par les perpendiculaires aux bissectrices, on construit les bissectrices extérieures. On se place dans un contexte où les trois centres des cercles exinscrits existent. Ce sont les points \(M, N, P\). La propriété que l’on va illustrer est vraie aussi avec les équidistantes, c’est bien entendu une propriété des pinceaux de droites, indépendante de la nature du cycle, mais pour un premier contact avec le modèle KB, on a préféré ne pas ajouter les macros des pinceaux de droites.
Puis on construit les projetés orthogonaux, sur la droite \((BC)\) des centres des 4 cercles. On note ainsi \(h_I, h_P, h_M\) et \(h_N\) le pied de la perpendiculaire issue du centre correspondant,\(I, P, M\) et \(N\) respectivement. Si on avait une équidistante à la place d’un cercle, il aurait fallu utiliser la droite du pinceau associé à l’équidistante, orthogonale à \((BC)\). Mais, comme déjà mentionné, cette macro n’est pas proposée ici.
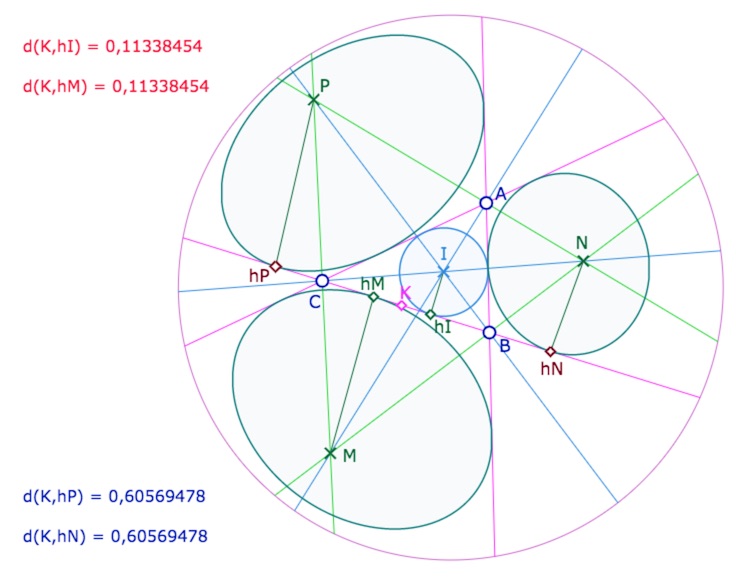
Puis on utilise la macro KB Distance 2 pts, et on s’aperçoit – constate ou illustre – de \(K\) est le milieu des points de contact d’une part du cercle inscrit et du cercle exinscrit directement opposé, et d’autre part des deux autres cercles exinscrits avec la droite \((BC)\).
Note d’interface : nous avons mentionné plus haut le changement de nom de la variable dMNxx qui donne la distance de deux points. Mais ici les expressions de type d(K,hX) ne sont pas des changements de nom des variables, mais des commentaires texte. Ils ne se traitent pas dans l’outil « aspect des objets » mais dans l’outil « expression » (icone calculatrice). Ne pas oublier de valider par le bouton vert.

La première ligne renvoie le calcul effectué par la macro (avec le nom de la variable à gauche),
la seconde ligne permet à l’utilisateur de rédiger un commentaire.
Pour faire cette figure, lancer à nouveau la figure de base avec toutes ses macros KB.
On peut aussi ne pas avoir le temps de « jouer avec KB » et préférer ouvrir la figure finalisée.
Éléments de preuve de cette propriété
Dans un futur menu Bachmann, on montrera cette propriété dans un cadre absolu. En attendant, on peut voir le principe de cette preuve, dans le cadre euclidien, où la propriété est assez immédiate.
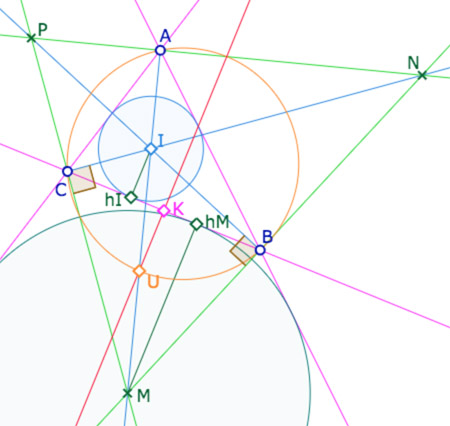
Dans le contexte euclidien, la preuve que \(K\) est milieu des contacts du cercle inscrit et du cercle exinscrit opposé est une conséquence de
• la cocyclicité des points \(I, C, M, B\), sur le cercle de diamètre\([IM]\).
• l’intersection \(U\) de la bissectrice \((AI)\) avec le cercle circonscrit à \(ABC\) – par des arguments d’angle – est sur la médiatrice de \(B\) et \(C\).
• Le centre du cercle passant par \(I, C, M, B\) étant à la fois sur la bissectrice \((AI)\) et sur la médiatrice de \([BC]\), c’est donc le point \(U\).
• Et donc par projection, \(K\) est à la fois milieu de \(B\) et \(C\) et de \(h_I\) et \(h_M\).
Cette première propriété étant acquise – c’est ce qui est le plus délicat à montrer de manière absolue, hors cocyclicité – le reste est assez immédiat, même dans un contexte général puisque l’on n’utilise que des symétries.
Voyons l’argument général, en reprenant la figure dans KB.
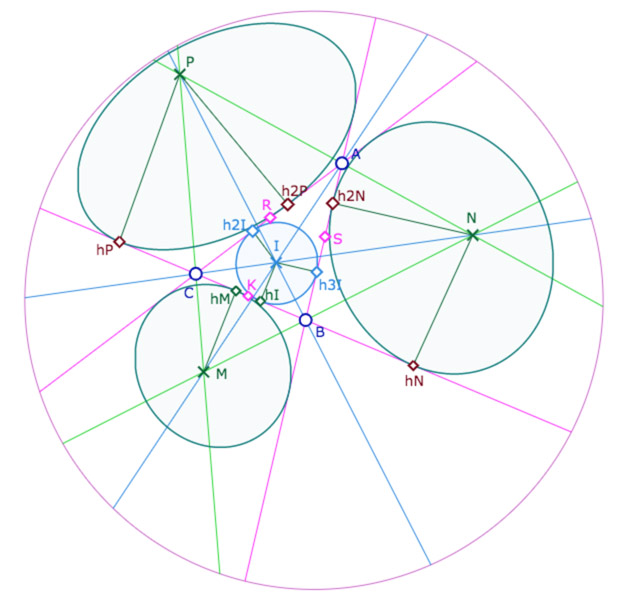
On nomme \(R\) le milieu de \(A\) et \(C\), et \(S\) celui de \(A\) et \(C\). On a la même propriété des contacts sur ces deux côtés. Partons du point de contact \(h_P\) du cercle de centre \(P\) sur \((BC)\). Son symétrique par rapport à la bissectrice \((MP)\) est le contact de ce cercle sur \((AC)\), soit le point \(h_{2P}\). Son symétrique par rapport à \(R\) est le contact sur cercle inscrit, soit le point \(h_{2I}\). Le symétrique de ce point par rapport à la bissectrice \((AM)\) est le point \(h_{3I}\). Son symétrique par rapport à \(S\) est le point de contact du cercle de centre \(N\), soit le point \(h_{2N}\). Enfin le symétrique par rapport à la bissectrice \((MN)\) est le point de contact \(h_N\).
On à donc \(h_N = s_{(MN)} \,o \, s_S \, o \, s_{(AI)} \, o \, s_R \, o \, s_{(MP)} \; (h_P)\).
Dans le cas général \(s_{(MN)} \, o \, s_S \, o \, s_{(AI)} \, o \, s_R \, o \, s_{(MP)}\), composée de trois symétries orthogonales – de droites en faisceaux – en alternance avec deux symétries centrales échange \(B\) et \(C\) et laisse la droite \((BC)\) globalement invariante. Dans le cas euclidien, en prenant le vectorialisé des applications, la symétrie centrale est exclue, donc la composée est la symétrie orthogonale d’axe la médiatrice de \([BC]\). Ce qui achève la preuve euclidienne.
La preuve absolue consiste à montrer ce résultat par les propriétés des droites en pinceau. Elle est proposée dans cet article publié depuis.