Milieu et symétrique algébriques dans KB
Dans la présentation des macro-construction du modèle de Klein Beltrami, nous n’avions pas proposé de macro « milieu », il fallait utiliser la médiatrice de deux points pour construire un milieu. Ce n’était pas essentiel car il s’agissait de ne construire que quelques milieux.
Mais pour construire les milieux et surtout massivement des symétriques de symétrie centrale, il devient nécessaire de calculer les coordonnées d’un KB-milieu et d’un KB-symétrique d’autant que c’est en fait très simple … ce qui révèle aussi une certaine paresse, parfois, de l’auteur de ce site … pourquoi ne pas l’avoir fait avant ?
Le milieu algébrique
On rappelle que la distance de deux points \(A\) et \(B\) est donnée par \(d(A,B) = \displaystyle \frac{1}{2} \left\vert ln \left(\frac{AU}{AV} : \frac{BU}{BV}\right) \right \vert\).
L’égalité \(AB=2AI\) aboutit à \(\displaystyle \left( \frac{IV}{IU} \right)^2=\frac{AV.BV}{AU.BU}\).
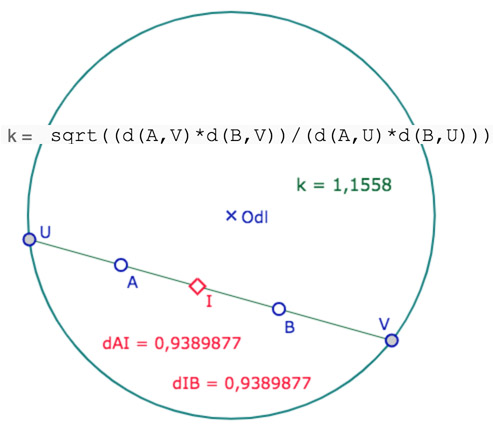
Or on sait que la ligne de niveau \(\displaystyle \frac{MA}{MB}=k\) est un cercle de diamètre \([RS]\) avec \(R=\displaystyle \frac{A+kB}{1+k}\) – entre \(A\) et \(B\) – et \(S=\displaystyle \frac{A-kB}{1-k}\). C’est donc l’écriture de \(R\) qu’il faut retenir pour le KB-milieu.
Lancer une figure sur la ligne de niveau (s’ouvre dans un autre onglet)
En pratique, pour éviter de créer autant d’expressions intermédiaires que de milieux utilisés, on a choisit d’intégrer \(k\) dans l’écriture du point \(I\). De même, les points idéaux de la droite \((AB)\) peuvent servir plusieurs fois, on a donc crée deux macros dont une – la plus utilisée – demande les 4 points \(A, B, U, V\).
Le symétrique algébrique
Pour le symétrique \(B\) d’un point \(A\) par rapport à un point \(I\), on trouve \(\displaystyle \frac{BV}{BU} = \frac{AU}{AV} \times \left(\frac{IV}{IU}\right)^2\).
Bien entendu les points \(U\) et \(V\) sont les points idéaux de la droite \((AI)\). Mais, comme on va utiliser une animation sur le point de troncature, ce point va être à un moment superposé au point \(I\). Dans ce cas, la droite disparait … et toute la figure construite sur ce symétrique avec. Pour remédier à cela on peut envisager une modification de type « programmation paresseuse » comme ceci :
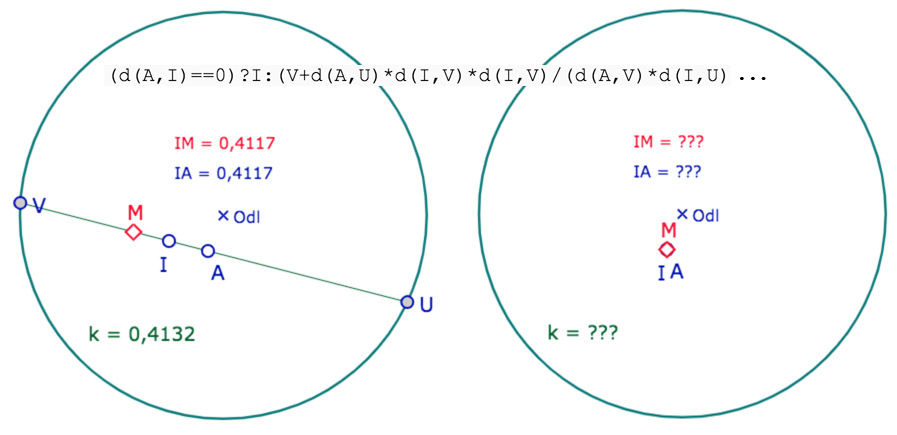
Dans l’expression ci-dessus, le symétrique de \(A\) est déclaré étant \(I\) si \(A\) est en \(I\) sinon on fait le calcul (ci-dessus incomplet, car trop long). L’illustration de droite montre que quand la droite disparaît, quand \(A\) est en \(I\), le point \(M\) existe toujours car, dans l’expression, seul le cas concerné est évalué.
Mais quand on transforme cette construction en macro, la subtilité de la programmation paresseuse du test JavaScript, opérationnelle ci-dessus, disparait, probablement car les points idéaux sont évalués (construit) juste avant le test.

Mais finalement on n’a pas besoin de mettre en œuvre des procédures aussi générales, avec le centre de symétrie en manipulation directe puisque les centres que l’on va utiliser seront déjà construits. On va donc utiliser simplement la construction de base, mais à partir des points idéaux de la KB-droite qui contient ce point, souvent déjà construits par ailleurs. Cela demande juste à l’utilisateur de montrer 4 points initiaux pour construire un symétrique, mais cela a l’avantage de construire ce point sans aucun objet intermédiaire. Là encore on construit deux macros pour la symétrie centrale, selon que les points idéaux sont déjà construits ou non.
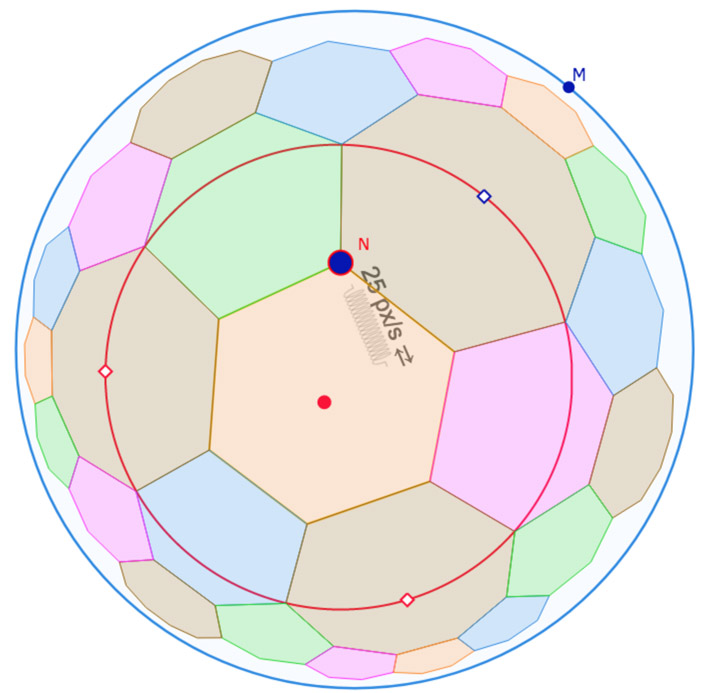
Troncature de P54
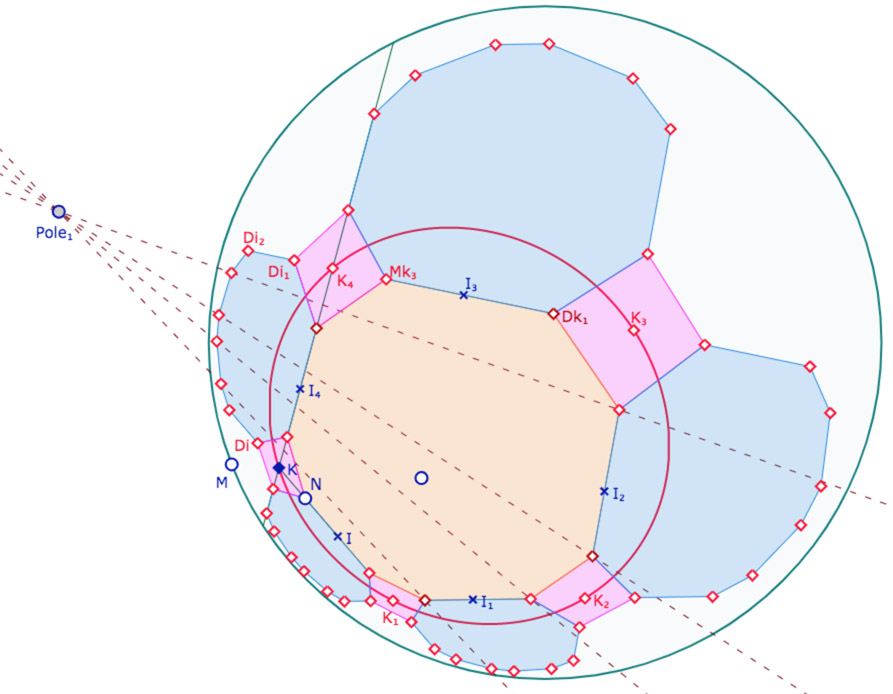
On reprend les méthodes déjà utilisées pour les pavages de KB. On ne revient pas sur les détails génériques. Abordons la troncature du pentagone initial \(KK_1K_2K_3K_4\) à l’intérieur du cercle de pavage. On a donc un décagone.
Étape 1
On nomme \(I\) est le milieu de \([KK_1]\) et on prend un point \(N\) sur le segment \([KI]\).
La première étape consiste à prendre les symétriques de ce décagone par rapport aux côtés du pentagone initial. C’est la même méthode que dans les pavages, avec le pôle du côté, par division harmonique. Par exemple les points \(Di_1\) et \(Di_2\) sont les symétriques de \(Mk_3\) et \(Dk_1\) car ces point sont alignés sur \((K_3K_4)\). \(Di_1\) est aussi le symétrique de \(Mk_3\) par rapport à \(K_4\) car l’angle en \(K_4\) est droit. De même, \(Di\) est le symétrique dd \(N\), à la fois par rapport à la droite \((KK_4)\) et par rapport au point \(K\). Le premier symétrique du décagone effectué, on transforme cette partie en macro appliquée aux quatre autres côtés.
Étape 2
Les cinq autres décagones sont les symétriques du décagone central par rapport aux sommets du pentagone initial. On termine la figure par les dix carrés. Il ne manque qu’un point pour chaque carré. Les macros de la symétrie centrale sont utilisées, en tout, 55 fois dans cette figure.
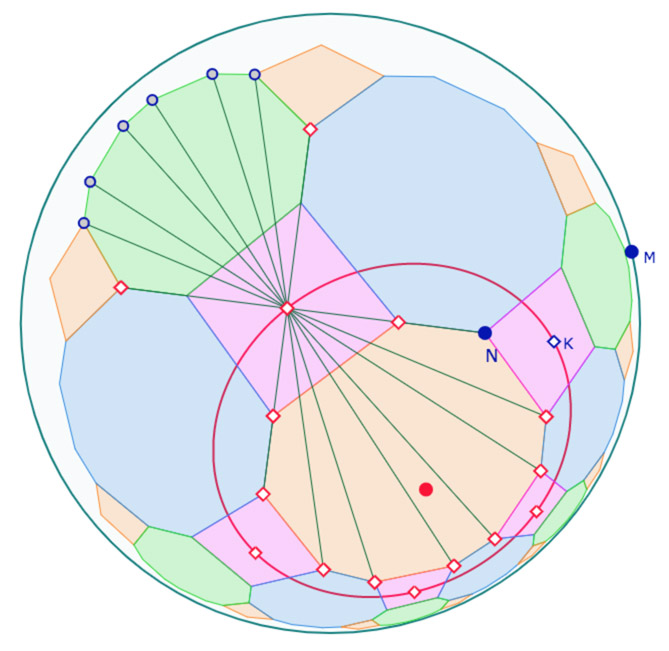
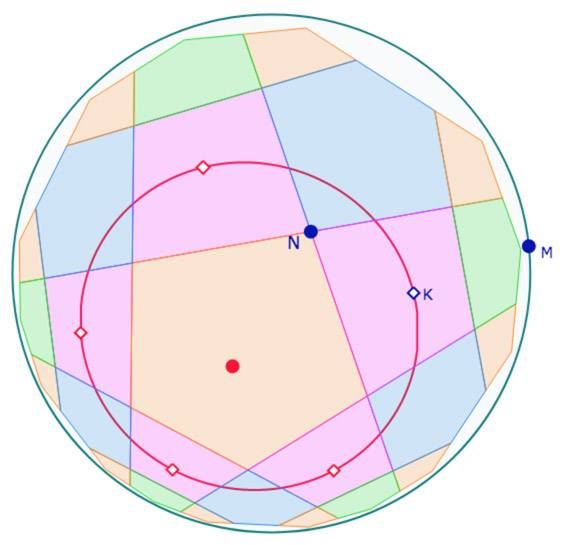
Cas où \(N\) est en \(I\) : pavage de pentagones (non orthogonaux) et de carrés de mêmes côtés.
La figure dynamique
Dans cette figure, on peut déplacer le centre du cercle de pavage pendant les deux animations
Préférer lancer la figure (sans restriction) dans un nouvel onglet.
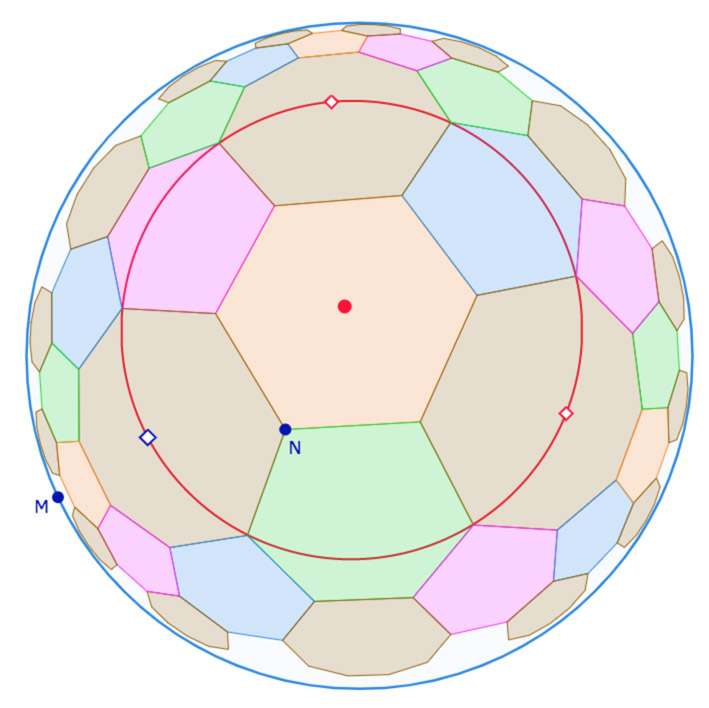
Troncature de P64
Les hexagones orthogonaux se transforment en dodécagones. Comme on part d’un hexagone, la symétrie centrale est est encore plus utilisée que dans la figure précédente. La construction est donc proche de celle de la figure précédente. On propose directement la figure finale.
Mais pour le plaisir de lancer soi-même la seconde animation, il n’y a que le point \(N\) d’animé. Pour animer le point \(M\) il faut :
• être en mode standard (la flèche de gauche active)
• puis cliquer sur \(M\) et choisir l’outil de comportement « ressort » (dernière icone en bas à droite)
• mettre le ressort à 30 ou 45 pixels/s
Faire la manipulation proposée ci-dessus. Puis déplacer le centre du cercle de pavage pendant les deux animations
Préférer lancer cette figure dans un nouvel onglet (et faire la seconde animation)
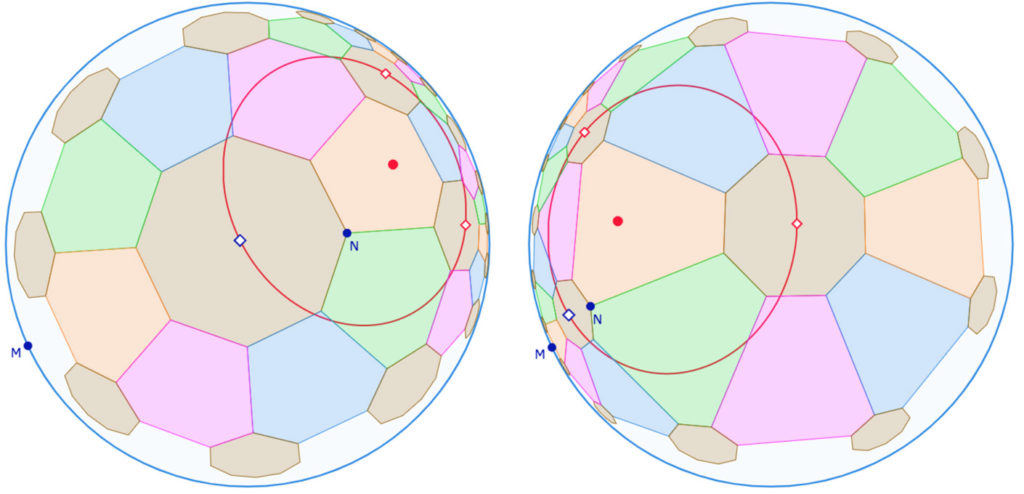
Troncature de P38
On a ici un pavage de triangles d’angles au sommet de 45°. Les 8 triangles autour d’un point forment un angle plat par groupe de 4triangles successifs. Il y a donc beaucoup de symétries centrales pour finaliser la figure. Voici une image de la troncature quand elle est nulle, soit le point \(N\) en \(K\).
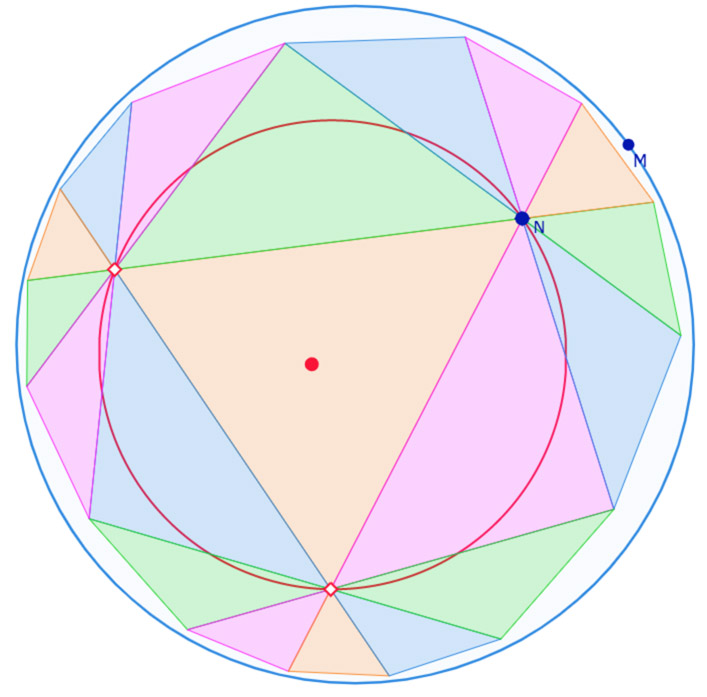
La troncature est donc composée d’hexagones et d’octogones, dont les trois premiers autour des sommets \(K, K_1, K_2\) comme on les voit ci-dessous. Dans cette illustration, on a ajouté trois autres octogones
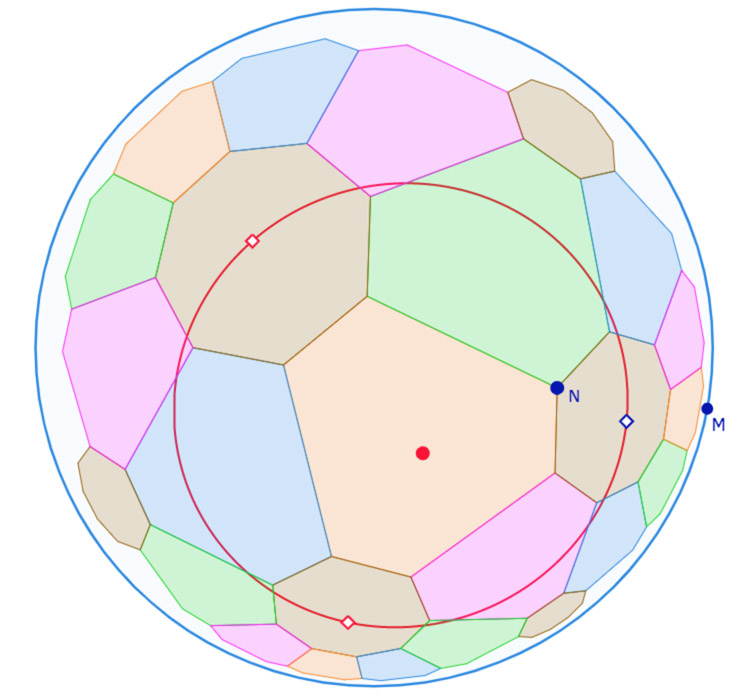
La figure précédente est assez longue à lancer (de l’ordre de 45 s), c’est pour cela qu’on propose de l’ouvrir dans un autre onglet. Elle est sans animation.
Remarque technique : pour ajouter une animation aller-retour sur un segment – cas du point \(N\) – il faut que l’inclinaison du ressort par rapport au segment soit d’un angle de plus 45°, on voit alors apparaitre une icone d’aller retour à côté de la vitesse, comme cela :
Suite de la figure
Dans la figure précédente, autour de chacun des trois octogones centrés sur les sommets du triangle initial, on a donc construit 4 octogones dans le prolongement de 4 des 8 rayons de ces octogones. On poursuit la figure on ajoutant quatre octogones autour de chacun des trois de base, soit donc 12 autres octogones.
Pour les lecteurs très curieux ou très motivés, on peut lancer cette nouvelle figure dans un nouvel onglet, sachant que la figure n’apparaîtra que dans une quinzaine de minutes (en moyenne dépend du processeur).
Une fois ouverte, la figure est très fluide, c’est seulement le temps de chargement qui est prohibitif, dû probablement à l’utilisation massive de macro-constructions.
Les troncatures réalisant
un polygone régulier
Pour les deux troncatures, il y a toujours une position du point \(N\) pour lequel le décagone (dans P54) ou le dodécagone (dans P64) est un polygone régulier. Au lieu de calculer – avec le trigonométrie hyperbolique – la position de \(N\) solution de cette régularité, on se propose de programmer la position de \(N\), avec Blockly, comme on a programmé les droites du modèle de Hilbert de la géométrie non arguésienne.
Dans l’illustration ci-dessous, sur la troncature de P54, on nomme cCarre la KB-longueur du côté des carrés (rose) de la troncature, et cPoly la KB-longueur de l’autre côté (bleu) du décagone.
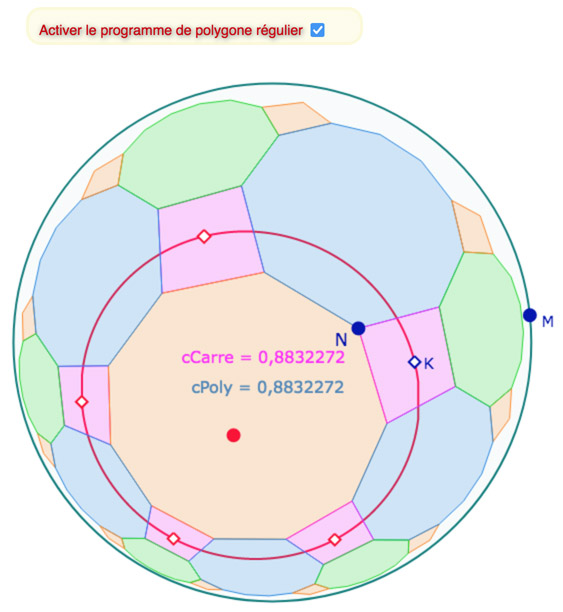
Le code Blockly est, comme dans d’autres pages de ce site, une dichotomie élémentaire.
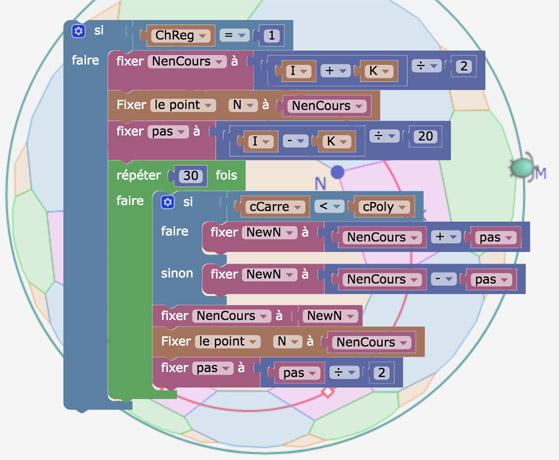
Lancer cette figure dans un nouvel onglet.
Utilisation : déplacer \(N\) juste pour voir la différence des deux longueurs s’afficher en temps réel. Puis cocher la case qui lance le programme.
Manipulation de la figure : ensuite, on peut déplacer \(M\) et surtout le centre du cercle de pavage. Comme il n’y a qu’un pavage P54, la valeur numérique de l’égalité des deux côtés est constante, indépendante de la position du centre du cercle de pavage. On notera qu’avec cette programmation, la figure est moins fluide, bien évidemment. Le code Blockly est dans le point \(M\).
Relancer la figure pour désactiver le code : si vous désactivez le code en décochant la case, le point \(N\) ne redevient pas un point sur objet, il devient un point libre, et donc ne restera plus sur le segment \([KI]\). D’où l’intérêt de travailler sur une figure en ligne, puisque que l’on peut relancer la figure initiale, en rechargeant la page, pour avoir à nouveau \(N\) sur le segment \([KI]\).
Version P64
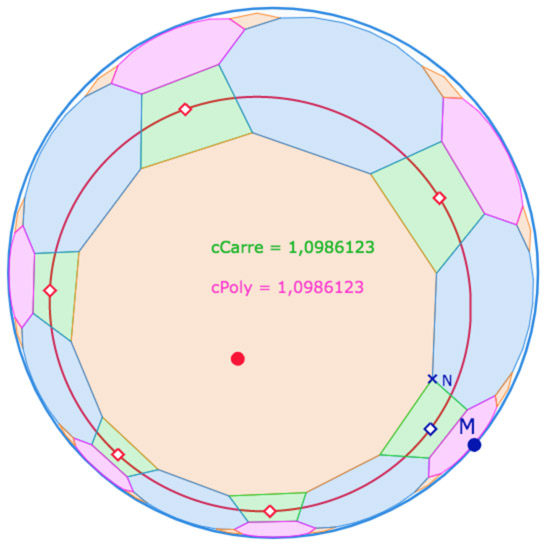
Lancer cette figure dans un nouvel onglet. Mêmes consignes qu’à la figure précédente.
Version P38
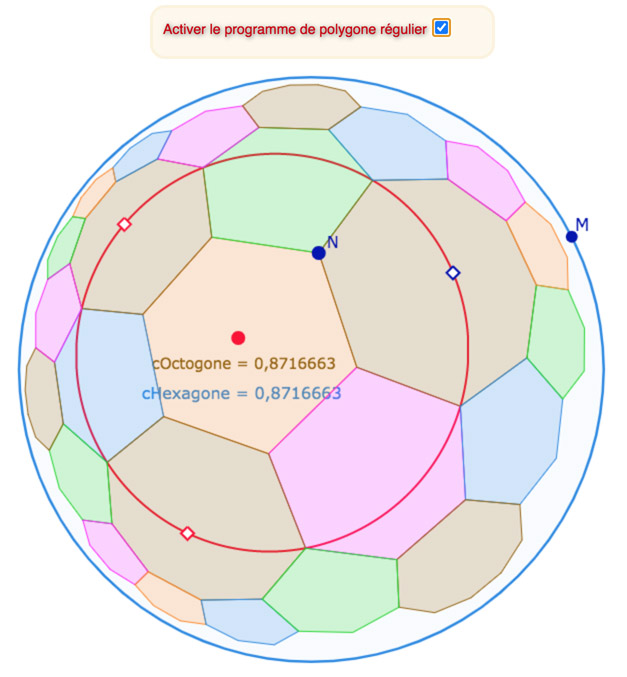
Lancer cette figure dans un nouvel onglet (toujours avec environ 45 s d’attente pour l’affichage).
Modification du code utilisé (toujours dans \(M\)) : pour placer \(N\) assez porche de la solution, on a dû l’initialiser à \(\displaystyle \frac{2I+K}{3}\) ou lieu de \(\displaystyle \frac{I+K}{2}\) .