Parmi la série de pages proposant de réaliser des figures hyperboliques dans un modèle, celle-ci est peut-être paradoxalement le meilleur rapport « investissement/satisfaction ». Bien entendu, même si les macros sont simples d’utilisation, faire des figures hyperboliques sur une surface 3D est un objectif non trivial, il faut donc rentrer dans la démarche retenue. Par exemple, il faut travailler à la fois dans KB, pour faire un figure préalable, et ensuite l’envoyer sur la PSH. C’est pourtant plus simple que sur la pseudosphère usuelle (PS) car, sur la PSH, comme on ne peut pas faire de constructions intrinsèques, le retour des objets sur la surface est, d’une certaine façon, automatisé. Par ailleurs, les figures obtenues sont assez superbes … d’autant qu’on propose en fin d’article un petit challenge bien sympathique.
Quelques pré-requis
Si on n’a jamais utilisé les macro-constructions de DGPad, on consultera d’abord cette présentation et on fera, éventuellement, quelques figures dans le modèle KB (lien ci-après) pour se familiariser dans un environnement non euclidien simple d’accès. Si on a déjà pratiqué les macros, on peut néanmoins éventuellement relire les premières lignes de l’article de présentation des macros de KB. En effet, on va les reprendre en partie, et les enrichir, dans une organisation structurées autrement.
Enfin, si on tombe un peu par hasard sur cet article, il faut bien entendu avoir vu quelques figures du menu PSH, au moins la présentation de la nappe pour comprendre pourquoi il y aura la liste LesCoef et la fonction g à passer en paramètre pour finaliser les figures sur la surface.
On travaillera sur deux figures préconstruites, proposées dans l’article, d’abord une pour les triangles et ensuite une pour les trilatères … avec là encore, une petite surprise sur les trilatères. On pourra bien entendu ajouter des points de base sur la pseudsophère hyperbolique. Voici une copie d’écran de la figure de base pour les triangles pour situer le contexte.

En particulier, on observera que l’on n’a pas tracé, a priori, les droites passant par les sommets du triangles, ni dans KB ni sur la PSH. Cela permet de choisir de tracer soit les droites soit les segments.
La première partie de cet article est dans la présentation du choix retenu pour la construction des objets sur la PSH, et de la façon dont sont articulées les macros pour y parvenir.
Lancer cette figure dans un nouvel onglet pour explorer les macros au fur et à mesure de la description.
Constructions finale sur la PSH
Il y a plusieurs façons d’organiser le retour d’une figure de KB sur une surface pseudosphérique. Par exemple, comme sur la pseudosphère usuelle (PS) on peut construire intrinsèquement les droites ou les cercles, les macros renverront seulement des coordonnées ou des paramètres qui seront ensuite utilisés par les macros intrinsèques. La méthode n’étant pas possible pour la PSH, on a retenu l’idée de renvoyer systématiquement le lieu d’un point courant (on dit en géométrie dynamique « point sur objet ») de l’objet construit dans KB. Cette unique macro fonctionne donc aussi bien pour les segments, les droites et même les cercles. Une autre macro fait quasiment la même chose mais ne renvoie que le point en question (nécessaire si on a un point d’intersection à construire par exemple).
La démarche utilisée est donc très simple :
– On construit la figure que l’on veut, dans KB, à partir des points images \(A_{kb},B_{kb},C_{kb}\).
– Sur chaque objet construit (segment, droite ou cercle) on place un point, et
– Une macro transforme ce point en le segment, la droite ou le cercle correspondant sur la PSH.
C’est assez magique, et c’est pour partager cela que cet article a été écrit.
Si on veut juste tester le principe rapidement, on peut s’amuser à le faire uniquement sur les trois droites du triangle \(ABC\), et remplir ce triangle sur la PSH, cela prend deux minutes. On peut aussi continuer avec les médianes … ou aller plus loin si on est plus concerné par ce modèle.
Organisation générale des macros
Les macros sont organisées en dossiers, trois pour le modèle KB, deux pour la PSH, et un dossier de Transfert dans les deux sens. A priori, avec les figures proposées à l’utilisation, on ne devrait pas avoir besoin du sens PSH vers KB, mais les macros pour ce passage sont disponibles si on veut ajouter des points de base.
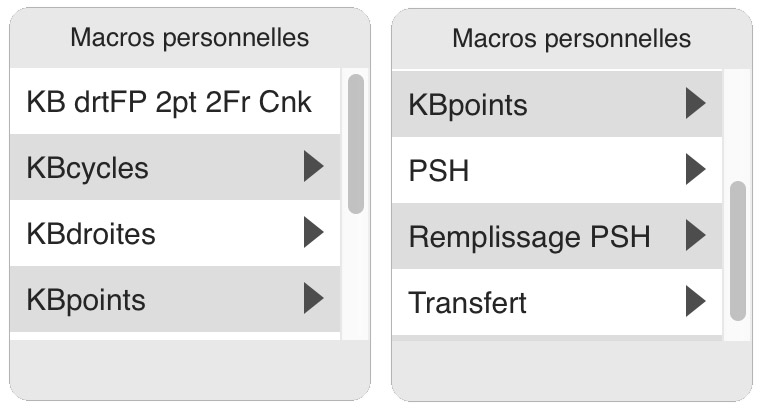
Le premier niveau des macros disponibles dans les figures
On notera en premier lieu une macro KB hors des menus KB. En effet, cette macro est propre à l’utilisation du modèle de Klein-Beltrami associé à une surface pseudosphérique hyperbolique. Elle est à considérer comme une macro de finition pour de belles figures, avec des droites bien lisses sur la PSH. Si on ne travaille qu’avec des segments par exemple elle est inutile. A priori son utilisation est donc à prévoir dans un second temps. Détaillons l’utilisation de cette macro.
KB drtFP 2pt 2fr Cnk : le code de cette macro a déjà été présenté succinctement, en particulier pour l’enchainement des points logiques internes, dans la section « Exemple des hauteurs » de la page sur les droites de la PSH mais son utilisation pratique n’a pas été détaillée. Cette macro construit, en toutes circonstances, dans le modèle KB, seulement la partie de la Feuille Principale d’une droite (drtFP) passant par 2 points (2pt) de KB, en donnant dans l’ordre ces deux points, les deux segments verticaux verts de l’illustration précédente – celui de gauche puis celui de droite – frontières de la feuille principale (2fr) puis l’équidistante frontière de la PSH, dans KB, à savoir la conique bleue (Cnk).
Contexte d’utilisation de cette macro : comme souvent dans ces cas, c’est plus long à décrire qu’à faire. On rappelle que sans cela, l’enroulement d’une droite sur plusieurs feuilles peut ne pas être esthétique.
Par contre un point important à signaler est que cette macro demande deux points de la droite. Or si on a pris, dans le menu KBdroite, une bissectrice, une perpendiculaire ou une perpendiculaire commune, il peut être nécessaire de construire (prendre sur la droite) un autre de ces deux points, voire les deux. C’est pour cela qu’il a été dit que cette macro est à utiliser « dans un second temps », sauf si on dispose déjà de deux points de la droite.
Les macros de KB

Les trois dossiers de KB
Les points
Par rapport aux premières macros de KB présentées dans cette page, nous avons ici ajouté les macros algébriques de milieu et symétrique par rapport à un point construites dans cette page sur les troncatures. En particulier on peut très rapidement construire les médianes.
Les droites
En plus des droites que l’on voit dans l’illustration, il y a également les bissectrices. On a aussi laissé les KB-droites de base. Mais comme ces macros demandent deux points, si on peut l’utiliser, a priori on utilisera plutôt la macro sur les droites FP (de la feuille principale).
La question du segment
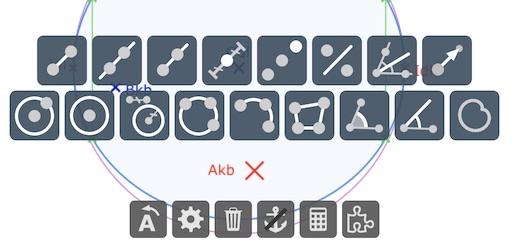
Un KB-segment est le segment euclidien de mêmes extrémités. On a choisi de ne pas en faire une macro. Cela signifie qu’on le construit avec l’interface de base du logiciel, donc en mode standard (la flèche gauche du tableau de bord activée), en sélectionnant un point on choisit l’icone de segment en haut à droite comme dans l’illustration ci-contre. On relâche la souris sur le point à l’autre extrémité du segment.
Les cycles
Dans un premier temps, a priori on utilisera seulement la macro sur le cercle qui reste dans l’équidistante limite de la surface, car les autres cycles sortant de cette limite, c’est un peu plus long à gérer correctement.
Les trois dossiers autour de la PSH

Les trois derniers dossiers
Les deux macros du dossier PSH
Pour une utilisation standard, ce dossier ne sera pas utilisé, il sert en effet à construire un nouveau point sur la surface. Pour cela on prend un point sur objet, uM par exemple, sur le segment vert porté par l’axe (Oz). On applique alors la macro Equidist LesCoef g uA qui construit le cercle 3D associé à cette latitude uM, et rend aussi son centre que l’on nomme oM dans la suite (il n’est pas nommé comme cela par la macro, et il n’est pas nécessaire de le nommer dans la figure).

à gauche : on prend un point sur l’axe, il faut choisir l’icone « point » à droite. Avant cela il faut être « en mode standard ».
à droite : on a construit le cercle latitude uM. Son centre oM (qui a la forme du point C) est souvent « sur » le point uM sauf aux extrémités de la surface, c’est pour cela qu’on déplace uM vers une des extrémités pour pouvoir appliquer la macro qui donne les coordonnées (pour bien distinguer le centre (2° point) et la latitude (3° point). On prend le point M sur le cercle 3D comme à gauche.
Le dossier Transfert
La première macro de ce dossier construit un objet sur la PSH à partir d’un point de KB.
Drt LesCoef g Odl Mkb : nommée Drt (pour Droite), elle s’applique aux segments, aux cercles (et même aux lieux en général). Dans l’illustration suivante, on se propose de construire le segment \([BC]\) sur la PSH.
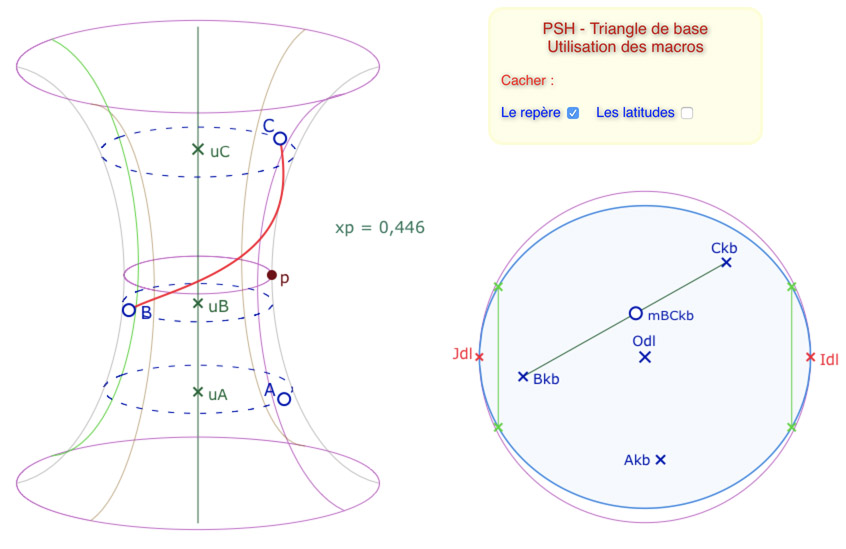
Étape 1 : on construit le segment \([B_{kb}C_{kb}]\).
Étape 2 : on prend un point sur objet de ce segment (même procédé que l’illustration précédente). Ici il est nommé \(mBC_{kb}\). Il n’est pas nécessaire de le nommer.
Étape 3 : on applique la macro précédente en montrant les deux expressions LesCoef et g (non présentes dans l’illustration), le centre du cercle \(Odl\), et donc, ce point \(mBC_{kb}\). La macro construit aussitôt le segment rouge sur la PSH.
Réglage de la densité
Par défaut la densité est réglée à 200, ce qui est suffisant en général pour une droite de la feuille principale. Par contre c’est trop pour un simple segment. On peut limiter la densité à 50 ou même parfois à 20 pour certains segments. Pour cela on sélectionne l’outil « inspecteur d’objets » (la roue du tableau de bord) et on sélectionne le segment sur la PSH.
Pt LesCoef g Odl Ptkb : cette macro s’applique comme la précédente, mais comme son nom l’indique (Pt), elle ne place que le point sur la PSH et pas un lieu.
PS vers KB xp CdA Odl : cette macro envoie un point de la PSH sur KB. Pour cela on donne xp (seulement), les coordonnées du point et le centre du cercle. Elle ne s’applique que si vous ajoutez un point à la PSH.
Les macros de remplissage
Elles sont élémentaires à appliquer. Dans une utilisation un peu rapide, on n’utilisera probablement que celle du triangle. Voici ce qu’elle donne.
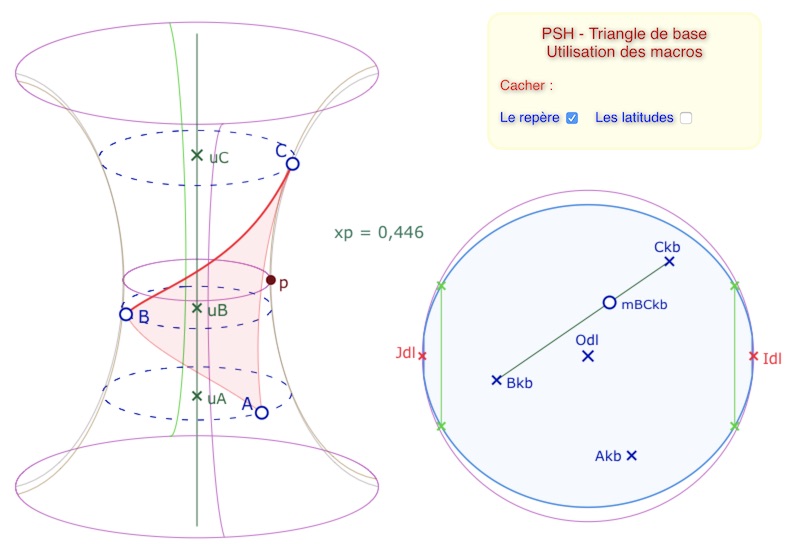
On remarquera le léger filet sur le pourtour du triangle, c’est parce que les segments de la liste de segments ne sont pas réglés à « 0 » car les points et les segments ne peuvent pas être tous les deux à « 0 ». Les modification (couleur, opacités) se règlent aussi dans l’inspecteur d’objets.
Les autres remplissages pourront être utilisés dans la dernière section Un morceau de troncatures que l’on propose au lecteur curieux … et un peu motivé quand même.
Remarque technique : on a présenté le remplissage des polygones sur la PS et la PSH dans cet article. Un lecteurs régulier de ces articles, et un peu vigilant, remarquera que l’on a enlevé la demande de l’expression xp dans la liste des objets initiaux de la macro. On a bien entendu modifié le code interne de la macro pour permettre cela.
Accompagnement de constructions pratiques
Si ce n’est pas déjà fait, lancer la figure de base dans un nouvel onglet.
La figure la plus simple à réaliser est celle-ci avec la macro KB DrtFP 2pt 2fr Cnk
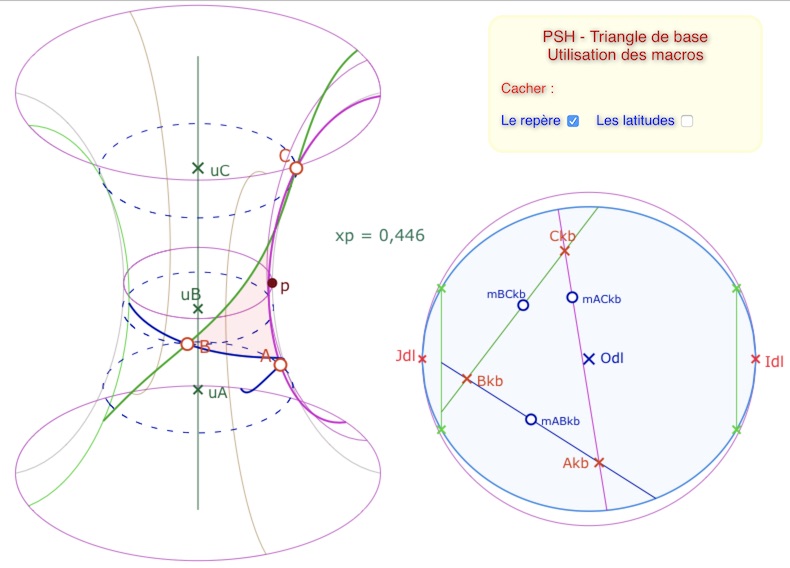
C’est intéressant de déplacer, sur la PSH, le point A ou sa latitude pour avoir une droite qui fait le tour de la feuille principale, son image sur KB allant d’un bord de la feuille principale à l’autre.
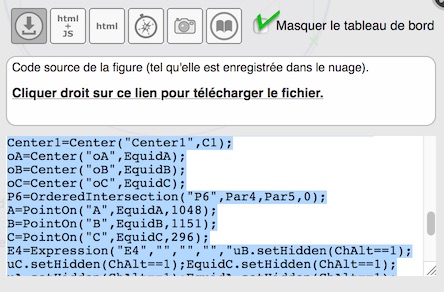
Enregistrement des figures produites
Pour télécharger votre figure, cliquer sur l’icone de téléchargement, celle avant les deux nuages dans le tableau de bord. Vous arrivez sur cette boite à dialogue. Enregistrer le fichier comme indiqué. Il s’appelle DGPad_file.txt.
Changer son nom, et lui mettre l’extension .dgp. Pour l’ouvrir, il suffit alors de déposer le fichier sur la fenêtre de travail de DGPad (en ligne ou desktopApp).
Exemple d’une démarche possible pour la construction des hauteurs
Comme on veut, au final, utiliser la macro KB drtFP qui demande deux points pour une droite, le plus pertinent est d’utiliser les pieds de hauteurs, pour les envoyer eux aussi sur la PSH. Il est préférable de
– Commencer par construire les KB-droites générales (peu d’objets intermédiaires), construire les pieds des hauteurs (illustration de gauche). Remarquer que l’usage des macros de KB cache le centre du cercle \(Odl\). Le faire réapparaitre (icone « gomme ») avant l’application des macros suivantes.
– Ensuite cacher les droites construites et construire les droites sur la seule feuille principale (illustration du centre)
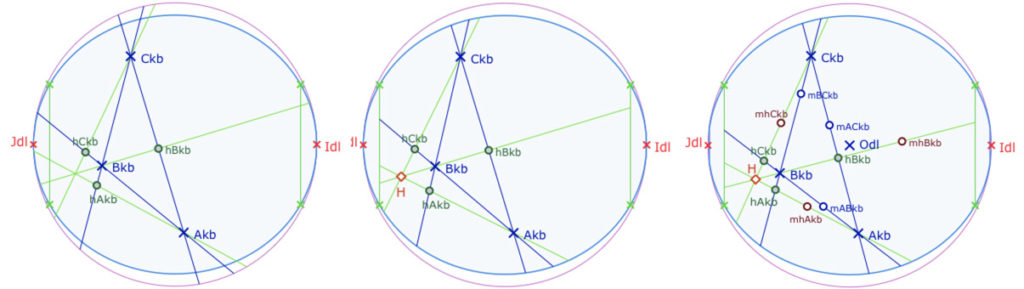
– Enfin, prendre des points sur chacune des droites pour renvoyer le tout sur la PSH. C’est l’illustration de droite. Il n’est pas nécessaire de nommer les points, ici ils sont nommés pour illustration. Puis on applique les deux macros de transfert, pour les lieux et les points, ce qui donne :
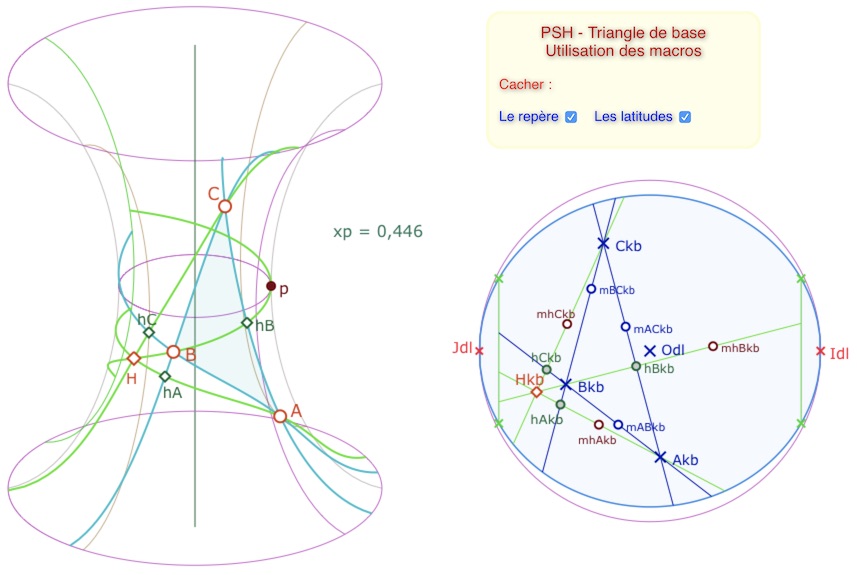
Ensuite, on traite le cas où les hauteurs ont une perpendiculaire commune. On fait de même qu’à l’étape précédente (KB-droite puis KB drtFP)
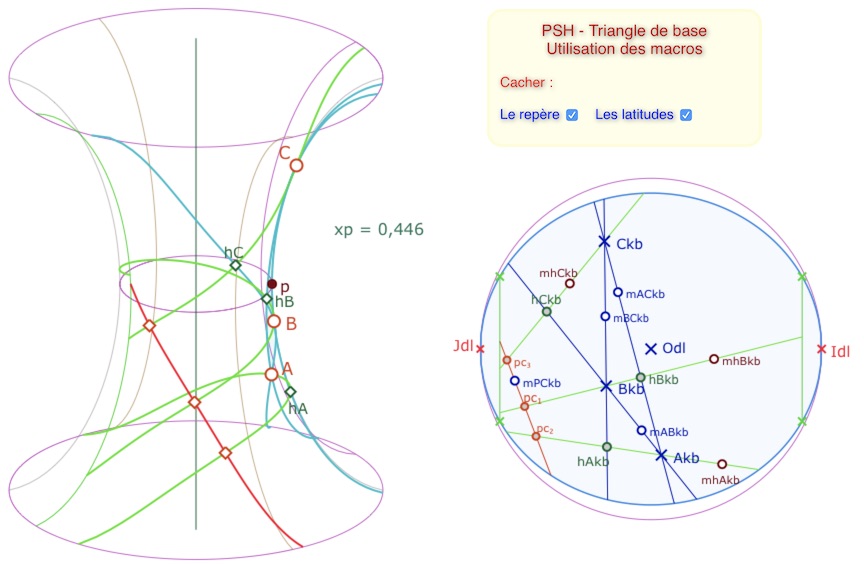
Enfin, bien entendu, on cache tous les points de construction intermédiaires (les \(mXYkb\)).
Le cas du cercle circonscrit au triangle
On fait de même avec les médiatrices. Partant des médiatrices, on dispose des milieux des segments. On peut ajouter un point (intersection avec la droite opposée) pour appliquer la macro KB drtFP. Dans l’illustration suivante, on n’a même pas tracé les médiatrices sur la PSH pour montrer que la macro Drt LesCoef g Odl Mkb s’applique bien directement au point \(mCirckb\) de l’ellipse (KB-cercle circonscrit au triangle).
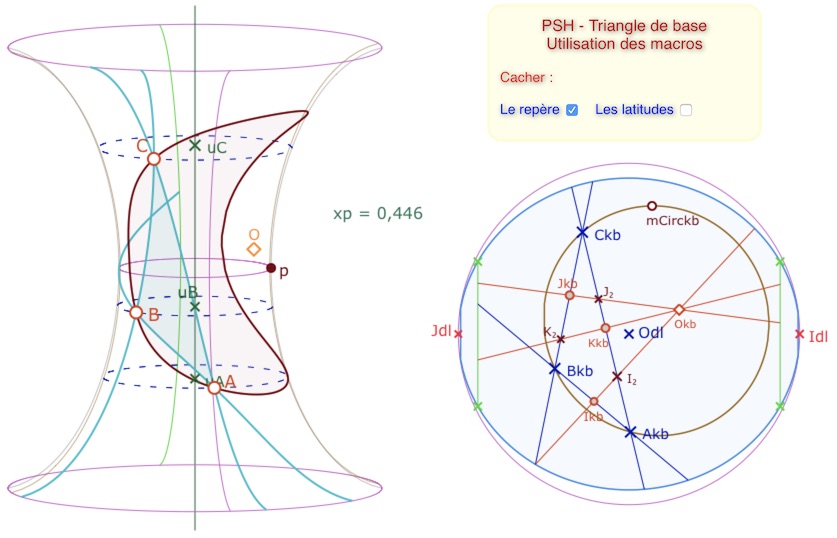
Application de la macro de tracé de droite pour obtenir le cercle circonscrit à ABC.
Les cercles sont par défaut tracés à une densité de 200. Néanmoins, pour que l’ellipse qui représente le KB-cercle soit correctement tracée, mettre une densité à 1000 (outil « inspecteur d’objets »). Pour les illustrations de cette page, dès qu’il y a un cercle il est à densité 1000 ou 1500.
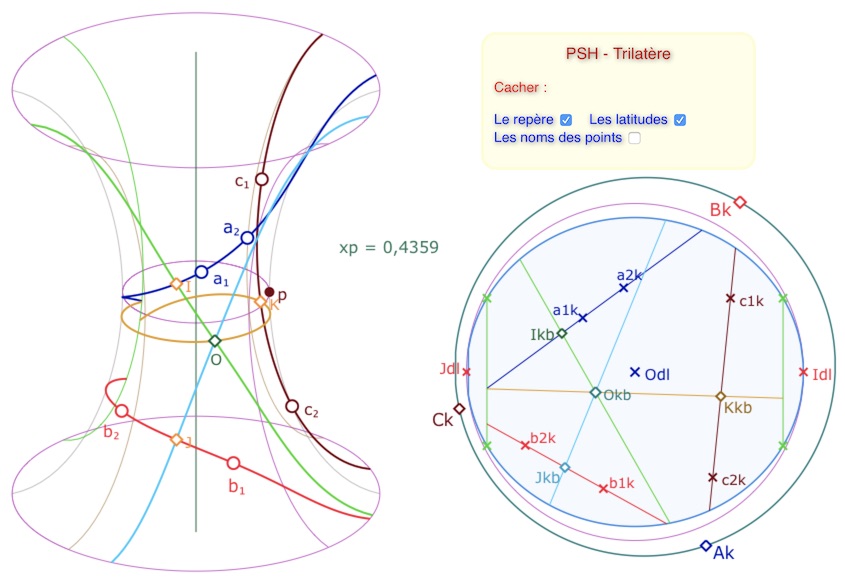
Quelques figures avec les trilatères de la PSH
On part de cette figure, où cette fois, les droites des trilatères sont pré-construites car il n’y a pas de choix entre segments et droites. Il y a 12 paramètres pour régler la position d’un trilatère, 6 points, deux par droite et les 6 latitudes de ces points.

Lancer cette figure des trilatères sur la PSH dans un nouvel onglet.
On utilise les mêmes macro-constructions que dans la figure précédente. Cela signifie que l’on ne dispose pas de macros spécifiques des faisceaux de droites dans KB. C’est en effet l’occasion d’utiliser, concrètement, le plongement projectif du plan hyperbolique. Nous en avons parlé succinctement dans cette page, dans le cadre du modèle DP. Dans KB, la situation est plus simple car le modèle KB étant déjà projectif, les calculs sont les mêmes, et donc les macros aussi. En pratique, on utilise les macros sur les sommets \(A_k, B_k, C_k\) du triangle du plongement projectif associé au trilatère (le prolongement des droites euclidiennes support du trilatère).
Exemple des bissectrices
Si on veut prendre la bissectrice des deux droites \((a1_{kb} a2_{kb})\) et \((b1_{kb} b2_{kb})\), on applique la macro Biss 3pts du dossier KBdroites sur les points \(a1_{kb}, C_k, b1_{kb}\). Dans l’illustration suivante, on a commencé par construire les bissectrices du trilatère, elles sont cachées, puis le cercle inscrit du trilatère, de centre \(I_{kb}\), et ses points de contact (avec la macro Perpendiculaire), puis les KB-droites passant par un sommet et le point de contact sur le coté opposé (en vert dans KB et sur la PSH). Ces trois droites sont concourantes en un point que l’on appelle le point de Gergonne, déjà présenté dans plusieurs modèles. Avant d’envoyer le tout sur la PSH, on utilise la macro KB drtFP à partir des points de contact et du point de Gergonne.
Dans cette illustration, on a fait entrer un des sommets sur la surface pour qu’on voit bien que la droite passe effectivement par le sommet. En faisant cette figure, bien entendu, on peut modifier les données des droites de base pour que le trilatère devienne aussi un triangle.
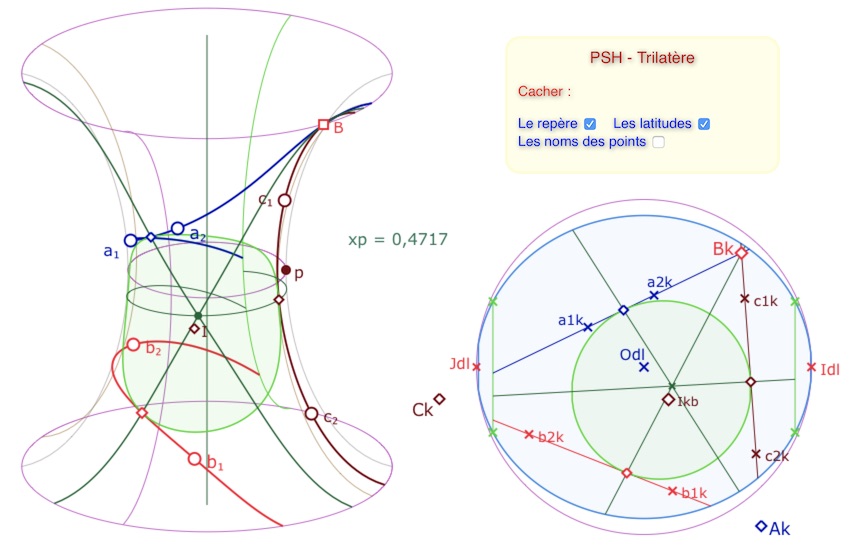
Construction du point de Gergonne d’un trilatère
On pourrait aussi refaire la figure sur les hauteurs proposée dans cette page, de la même façon. On peut aussi explorer une situation très simple, mais peut-être plus surprenante.
Les médianes d’un trilatère
Bien entendu le milieu d’une droite n’a pas de sens, mais dans le cadre d’un trilatère, on peut utiliser le plongement projectif de KB dans un plan idéal hyperbolique KH (présenté dans cet article). Dans ce contexte, le milieu de deux points simultanément intérieurs ou extérieurs au disque limite existe, et il est donné par les mêmes formules que pour les points tous les deux intérieurs au cercle limite. On peut alors construire le milieu des sommets du plongement avec la même macro Milieu Alg 2 pts du dossier KBpoints. On peut donc construire les médianes d’un trilatère, par plongement. Voici ce que cela donne :
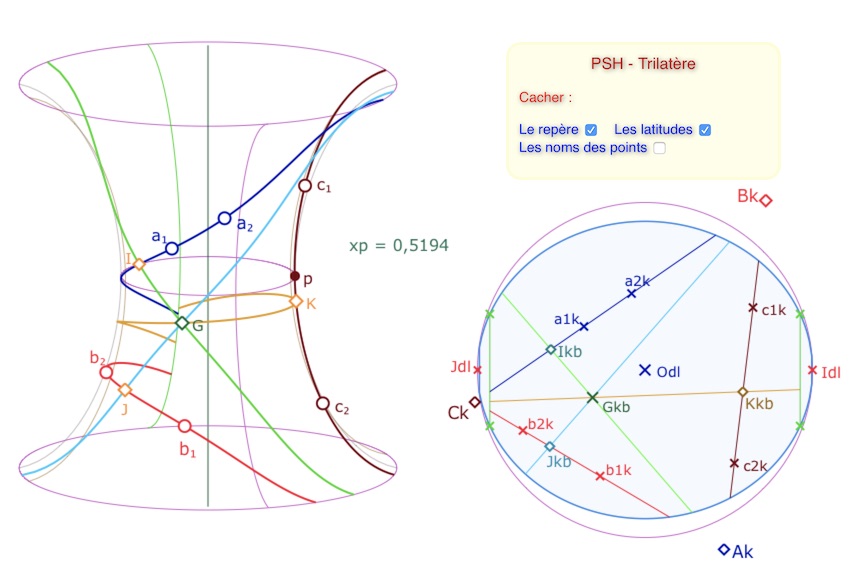
Les médianes d’un trilatère n’ayant aucun sommet sont concourantes
Si on fait cette figure, là aussi on peut rendre les trois sommets appartenant à KB et surtout existants sur la surface pseudosphérique. Attention, si on ne prend pas de précaution particulière (qui demanderait un peu plus de programmation), quand un point (par exemple \(IA_k\)) est intérieur et un autre (\(IB_k\) ou\(IC_k\)) est extérieur, les points produits par la macro « milieu » existent … mais ils ne peuvent avoir le sens de milieux hyperboliques. Nous y reviendrons dans un prochain article.
Les médiatrices du trilatère
Une fois que l’on dispose des milieux, on peut prendre la perpendiculaire aux côtés du trilatère en ces milieux. Le modèle KB n’est pas conforme mais le modèle PSH l’est, on voit bien, visuellement s’entend, sur la PSH, cette orthogonalité.
Ces médiatrices du triangle \(A_kB_kC_k\) sont concourantes en un point \(O_{kb}\) qui est le centre du cercle circonscrit au triangle … quand les trois points sont dans le plongement projectif hors de KB (sinon cela passe par l’inverse du point … on ne détaillera pas les aspects théoriques sous-jacents dans cet article … ce n’est pas le lieu, on est sur les macros de PSH).
Troncature de P54 sur la PSH
Pour le fun, pour les personnes qui aiment jouer avec la géométrie dynamique, voici une dernière proposition de construction sur la PSH. Dans cet article sur les troncatures dans KB on a déjà présenté cette troncature de P54.
Bien entendu, on ne va pas pouvoir envoyer toute la figure sur la PSH, car elle ne rentre pas dans l’équidistante limite de la surface, mais on voit bien que l’octogone central (au centre du pentagone de base, et, a minima, les 5 carrés autour peuvent facilement rentrer dans la PSH, en tout cas pour une étendue importante du paramètre \(p\). Voici ce que l’on propose au lecteur de réaliser, à partir d’une figure pré-construite.
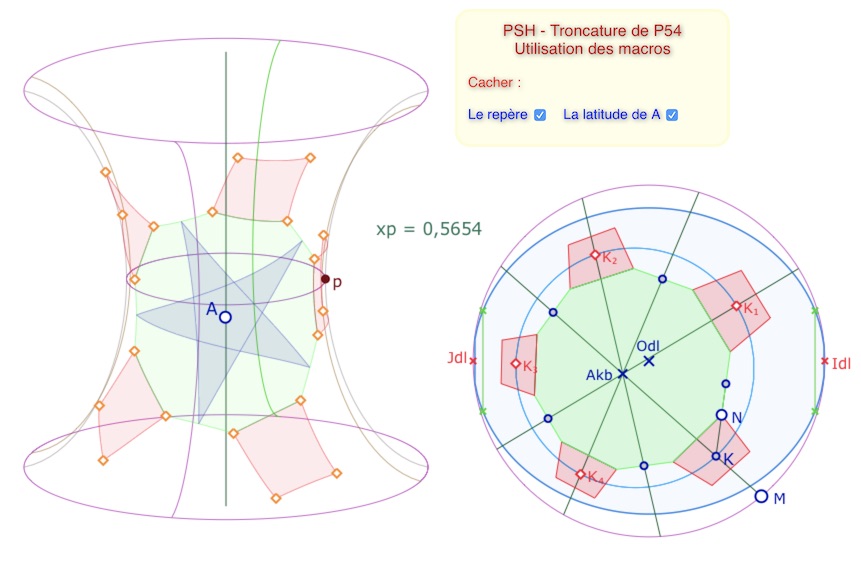
Sur la figure finale on pourra faire une animation sur \(M\), éventuellement sur \(N\) selon la façon dont on choisit de construire les symétriques.
La figure de départ et les nouvelles macros disponibles
On part d’un seul point de la surface, le point \(A\), centre de la configuration que l’on va construire, et en particulier centre d’un polygone orthogonal, d’image \(A_{kb}\) dans KB. Un point \(M\) sur le cercle horizon détermine un premier point \(K\) sur le cercle de pavage de P54.
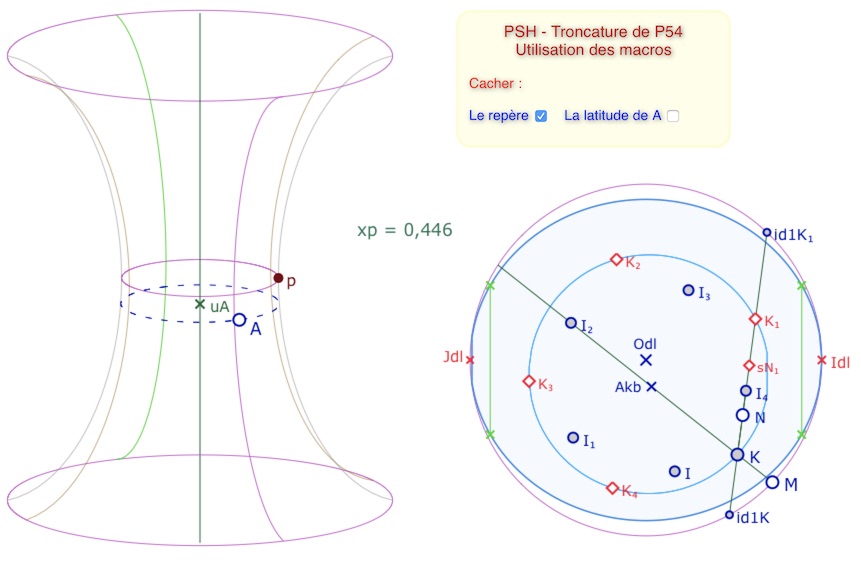
Lancer cette figure préparatoire dans un nouvel onglet
On dispose alors du pentagone orthogonal \(KK_1K_2K_3K_4\). Puis on a construit les milieux \(I, I_1, I_2, I_3, I_4\). Ensuite un point \(N\) est pris sur le segment \([KI_4]\). C’est le point de troncature.
La question des symétriques par rapport aux milieux
Dans la présentation des macros, le symétrique de \(A\) par rapport à un point \(I\) nécessitait juste ces deux points. Le calcul nécessite de tracer la droite \((AI)\), et donc le symétrique n’existerait pas si les deux points sont confondus, ce qui ferait effondrer la troncature dans ce cas.
On utilise alors une autre macro pour le symétrique qui demande 4 points, ci-dessus, les points \(I_4, N, id_1K,id_1K_1\), les deux derniers étant les points idéaux de la droite qui porte les deux premiers. Avec cette macro, le point \(N\) peut se superposer à \(I_4\), et son symétrique, ci-dessus, \(sN_1\) continuer d’exister et donc la figure aussi. L’ordre dans lequel on montre les deux points idéaux n’est pas important.
En préalable, il faut donc utiliser la macro Droite et Pts idéaux du dossier KBdroites à tous les cotés du pentagone initial, ce qui permet d’utiliser la macro SymC Ctr Pt 4 pts pour construire tous les sommets des carrés de troncature.
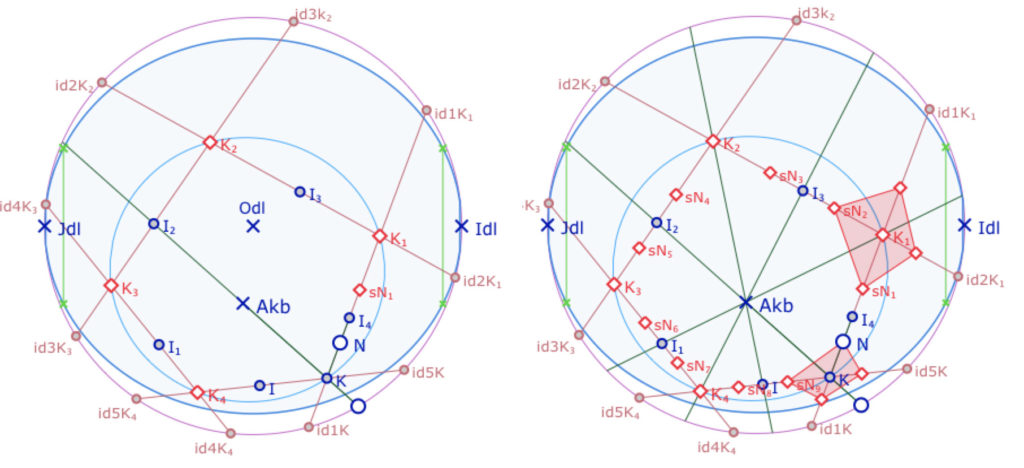
Début de la construction dans KB : on construit essentiellement des symétriques
par rapport à des points, parfois par rapport aux bissectrices (droites passant par le centre)
La réalisation de la figure
Pour changer de coté du pentagone, il faut aussi prendre le symétrique de \(N\) (par exemple, et des autres points) par rapport à la bissectrice en \(K\). On n’utilisera pas la macro Biss 3 pts, car les bissectrices sont simplement les droites passant par un sommet du pentagone et son centre \(A_{kb}\) comme on le voit dans la première illustration.
D’une manière générale, on a caché les noms des points (en décochant la case) pour que la figure soit lisible.
Bien entendu, il y a une macro pour remplir le décagone sur la PSH. Voici une première version de travail (intermédiaire).
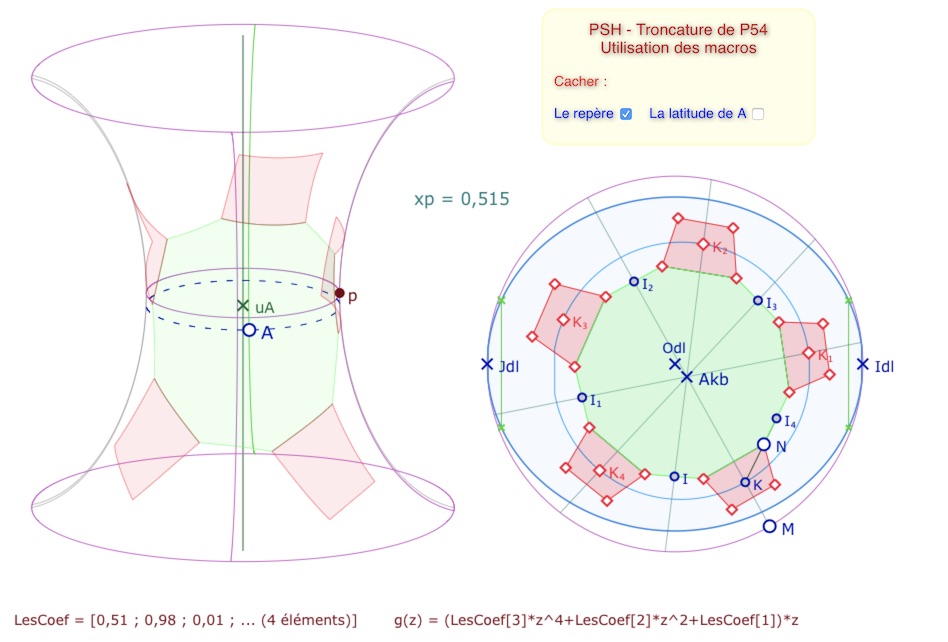
Voici un exemple d’illustration quand \(N\) est en \(I_4\), avec les sommets des polygones sur la PSH. On notera que l’on n’a pas tracé de segments sur la PSH.
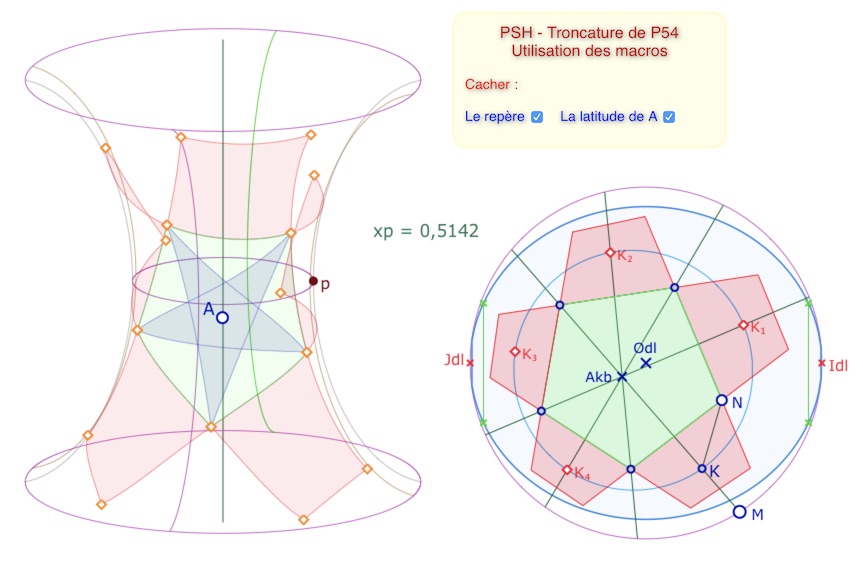
On peut aller plus loin : en élargissant l’équidistante limite, c’est-à-dire en diminuant la valeur de \(xp\), on peut faire entrer les 6 premiers octogones, le central et les 5 autour … mais sur trois feuilles de la PSH. On utilise essentiellement la macro SymC Ctr Pt 2pts, on construisant les symétriques de l’octogone central (en vert) par rapport à chaque milieu des cotés du pentagone initial, les points \(I, I_1, I_2, I_3, I_4\). C’est très rapide (sauf pour ajouter les sommets sur la PSH, il faut les faire un par un)
Ici, on affiche l’image des sommets pour bien vérifier que l’on reste sur la surface.
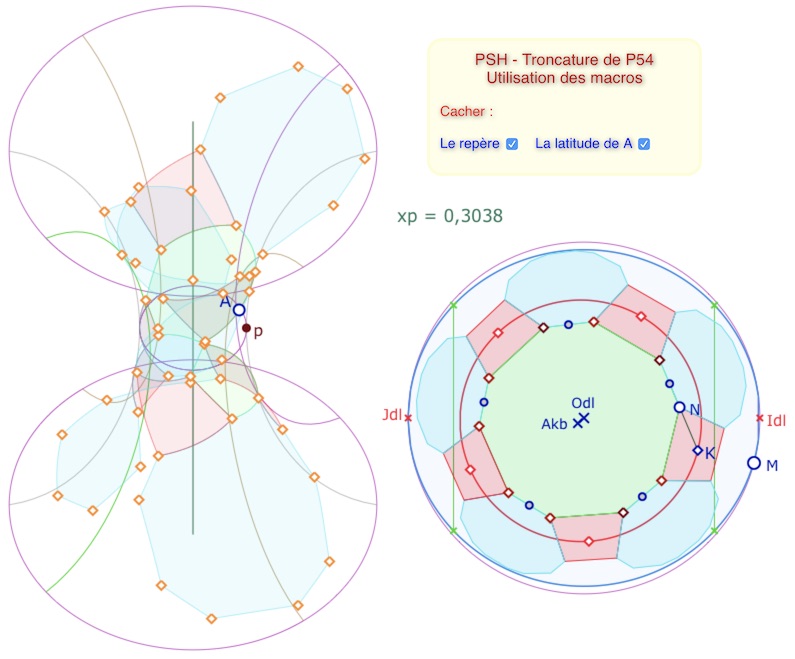
avec des carrés et des pentagones, ici, sans les sommets.
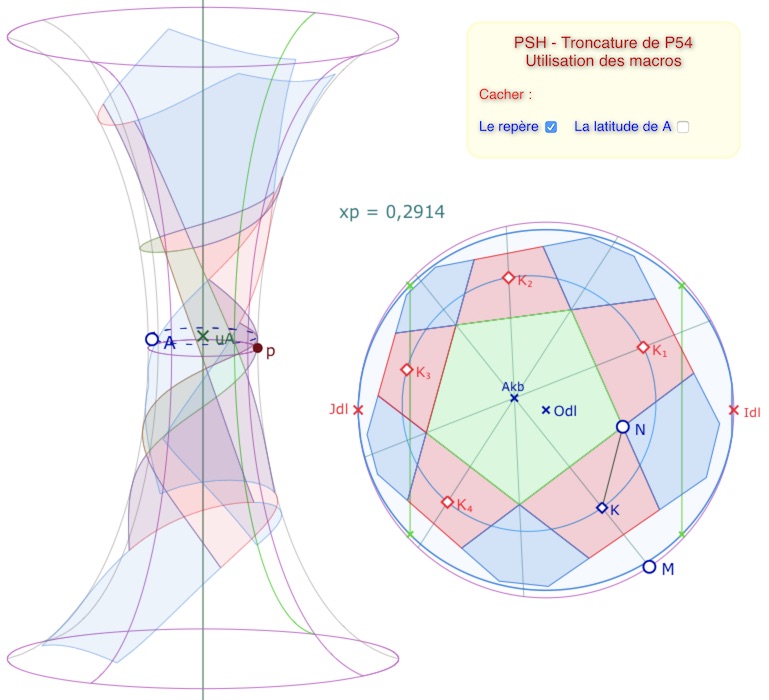
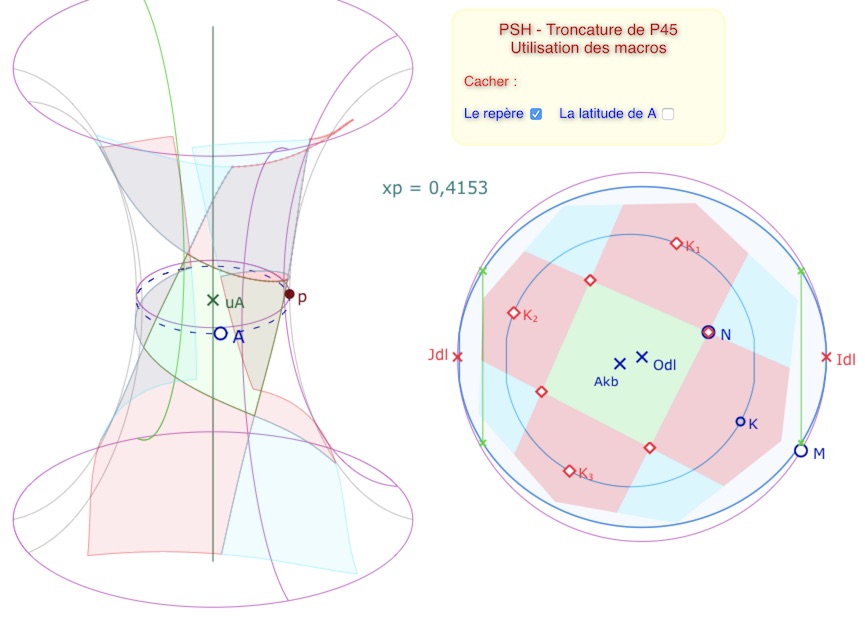
Troncature de P45 sur la PSH
On a déjà vu qu’il est facile de passer du pentagone orthogonal au carré à 72° depuis la figure précédente. On a présenté la manipulation dans un autre article, mais on propose ici de travailler directement sur la figure préparée à cet effet, avec, bien entendu, une macro de remplissage d’octogone sur la PSH puisque le carré central devient un octogone dans la troncature.

On part de cette pré-construction déjà avancée. Le départ est comme la construction précédente. Mais pour la construction des pentagones centrés en les quatre sommets du carré initial, il faut ajouter une nouvelle droite à chaque sommet. Par exemple depuis les points \(sN_1\) et \(sN_2\), on construit, par KB-symétrie orthogonale, les points \(Dk_2\) et \(Dk_3\). Mais pour construire \(Dk_4\), le dernier sommet du pentagone, on doit construire la droite \((K_1Dk_2)\). On rappelle que l’utilisation de ces macros cache le centre du cercle \(Odl\) qu’il faut remontrer avant le remplissage sur la PSH.
Lancer cette figure initiale dans un nouvel onglet
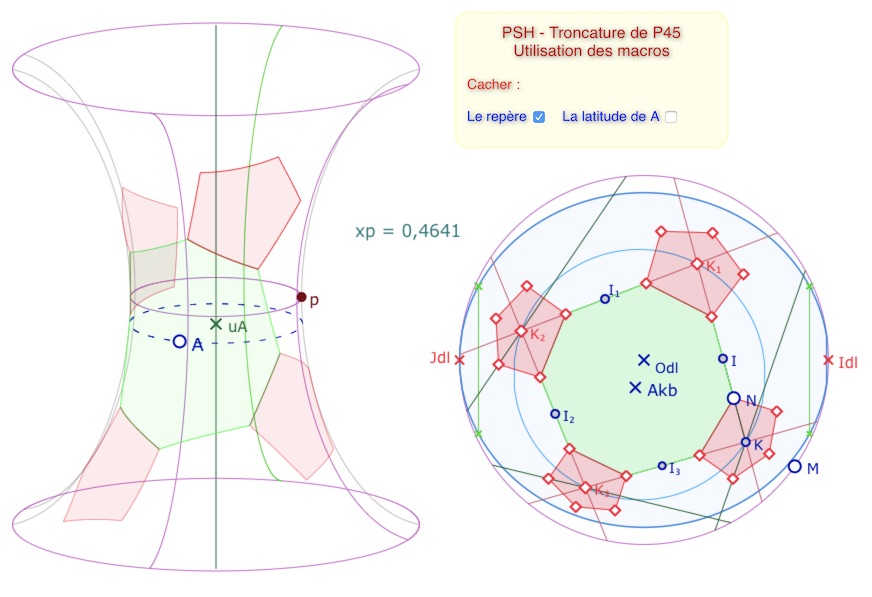
Puis on termine facilement la figure comme dans le cas précédent. La troncature rentre sur la PSH même pour des valeurs de \(p\) assez grandes.
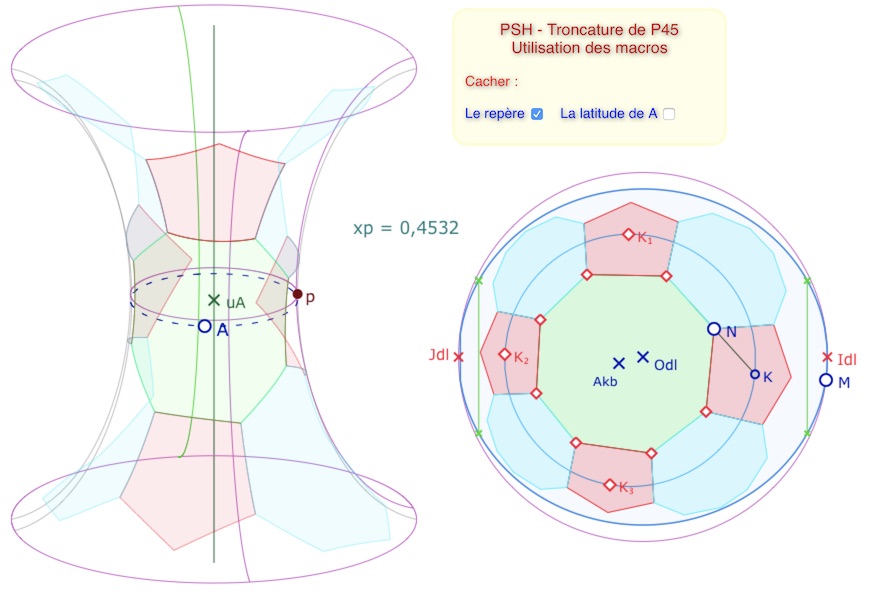
Voici une illustration dans le cas où \(N\) est au milieu de \([KK_1]\).
Pour les personnes qui n’ont pas le temps, voici les figures finales en téléchargement, même si le but de l’article est de proposer de les faire.