Nous poursuivons l’illustration du travail très approfondi de Daniel Perrin sur les modèles que nous avons appelé KE (elliptique) et KH (hyperbolique, plongement projectif de KB) présentés dans cette page d’introduction. La référence est toujours le PDF DPPartie4 de ce livre de Daniel Perrin, en cours de publication. Les numéros des pages mentionnées sont celles de ce fichier.
Cette page n’aborde que quelques uns des nombreux points développés dans les chapitres 4 et 5. Le chapitre 4 traite des invariants projectifs associés à une forme quadratique dans le cadre général d’un corps quelconque, et le chapitre 5 précise les spécificités de cette question sur le corps des réels.
On rappelle que, dans KH,
• Les points du cercle unité sont les points isotropes pour la forme quadratique associée.
• Les droites euclidiennes tangentes au cercle unité (droites isotropes) ne sont pas des droites de KH, et donc, par deux points appartenant à cette droite, on n’a pas l’axiome d’incidence de base de la géométrie.
• L’intérieur du cercle unité est le modèle de géométrie hyperbolique de Klein-Beltrami (noté KB dans ce site).
L’invariant « longueur » I(x,y)
Si l’on y réfléchit bien, la définition de la longueur est toujours tributaire de l’action d’un groupe. En effet, quand dit-on que deux bâtons ont même longueur ? Simplement lorsque, déplaçant l’un pour amener l’une de ses extrémités sur une extrémité de l’autre, on peut aussi faire coïncider les deux autres extémités. Qu’on appelle déplacement, mouvement, superposition … l’action ainsi effectuée, il s’agit toujours finalement de faire agir un groupe sur un ensemble et d’étudier sa double transitivité. C’est ce que nous faisons dans le cas des géométries non euclidiennes. Le tout est de trouver un invariant convenable.Il y a bien entendu les invariants vectoriels, \(q(a), q(b), \varphi(a,b)\) […]. Il s’agit de les transformer en invariants projectifs et on sait bien qu’il suffit pour cela de faire des rapports.
Daniel Perrin – Partie 4 – Chapitre 4 p age 143
Pour deux points \(a\) et \(b\) non isotropes, on définit \(\displaystyle I(a,b) = \frac{\varphi(a,b)^2}{q(a)q(b)}\).
Premières propriétés et première figure
• Tout d’abord \(I(M,N)\) est nul ssi \(M\) et \(N\) sont orthogonaux.
• Un cas particulier important est celui où \(I(A,B)=1\), ce qui correspond à une distance nulle. Pour deux points \(A\) et \(B\) non isotropes,\(I(A,B)=1\) si les deux points sont confondus, ou si la droite \((AB)\) est tangente au cercle unité.
• Pour deux points \(A\) et \(B\) non isotropes, tels que la droite \((AB)\) soit non isotrope, un point \(M\) de \((AB)\) vérifie ,\(I(M,A)=I(M,B)\) ssi \(M\) est milieu de \(A\) et \(B\).
Valeurs numériques de l’invariant (page 176)
• Pour KE, l’invariant de deux points \(M\) et \(N\) vérifie \(0 ≤ I(M,N) < 1\).
• Pour KH, si les deux points \(M\) et \(M\) sont
– intérieurs au cercle unité, \(I(M,N) > 1\)
– extérieurs au cercle unité et \((MN)\) non sécante au cercle unité \(0 ≤ I(M,N) < 1\)
– extérieurs au cercle unité et \((MN)\) sécante au cercle unité \(I(M,N) > 1\)
– l’un intérieur et l’autre extérieur au cercle unité \(I(M,N) < 0\)
Nous allons illustrer ces propriétés dans la figure dynamique suivante. Cette figure contient une droite \((AB)\), ses KE et KH pôles par rapport au cercle unité et les KE et KH milieux de ces deux points. Il y a aussi une tangente au cercle unité pour tester la propriété des droites isotropes et le point de contact avec le cercle (seul point isotrope de la figure). On dispose ensuite de trois points \(M, N, P\), et des KE et KH invariants \(I(M,N)\), \(I(M,P)\) et \(I(P,N)\).
Ces trois points \(M, N, P\) sont aimantés par les deux droites (à 20 pixels) et par tous points de la figure (à 5 pixels) pour illustrer les premières propriétés mentionnées
Utilisations de la figure
1. Commencer par placer un des points \(M, N, P\) sur la droite \((AB)\), et les deux autres sur les deux pôles de la droite. Les deux invariants sur \(M\) sont nuls.
2. Vérifier que les 4 milieux sont bien des milieux, au sens de l’invariant, y compris quand la droite \((AB)\) coupe le cercle.
3. Comment placer \(M, N, P\) pour que les trois valeurs de l’invariant KE (ou KH) soient nulles ? Pour que les trois invariants KH soient égaux à 1 ?
4. Comment placer \(M, N, P\) pour que l’on ait \(I(P,N)=I(M,N)\) simultanément dans KE et dans KH comme ci-dessous ?

Préférer ouvrir la figure dans un nouvel onglet
Bonus : chercher à obtenir ces deux résultats, d’abord sur KH

Puis sur KE et KH
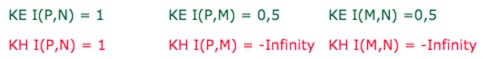
Rappel pratique : On modifie significativement la figures simplement en déplaçant le centre du cercle unité \(O_{cu}\) ou en modifiant son rayon, directement en tirant dessus à la souris ou au doigt.

Quand Euclide n’écoute pas (p. 144) …
Retour sur les cercles
Dans cette précédente page, nous avions définis la notion de cercle à partir des symétries orthogonales, sans aucune référence à une métrique ou a une expression numérique d’un rayon. Alors que l’invariant n’est pas encore une vraie distance (à peine une longueur, si une longueur peut être négative), on peut déjà illustrer que – comme on l’imagine bien – le cercle de centre \(O\) passant par \(A\) est bien l’ensemble des points \(M\) tels que \(I(O,M) = I(O,A)\).
Dans la figure suivante, en rouge le KH-cercle et en vert le KE-cercle, tous les deux, de centre \(O\) passant par \(A\). Les points apparents sont les points de construction de ces deux cercles – par symétries orthogonales.
On peut déplacer les points \(O\) et \(A\) ainsi que le centre du cercle et le cercle.
Les triangles ayant un cercle circonscrit « parabole«
On se propose aussi de « confirmer » que, dans l’article consacré aux « cercles-paraboles », on avait bien construit des cercles au sens de la ligne de niveau constante. Même si c’est superflu, c’est surtout l’occasion de manipuler l’invariant sur ces figures.
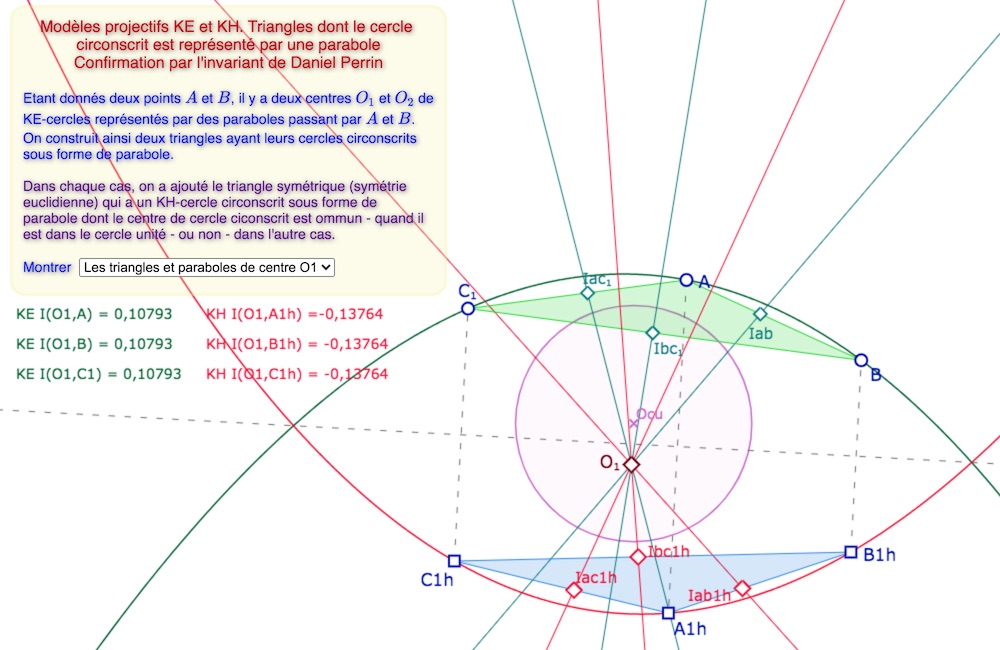
Dans cette première illustration, le centre \(O_1\) du KE-cercle parabole circonscrit au triangle \(ABC_1\) étant à l’intérieur du cercle unité, il est aussi (l’unique) centre du KH-cercle parabole circonscrite au triangle symétrique (dans la symétrie euclidienne d’axe \((O_1O_{cu})\). L’invariant KH a une valeur négative, parce que le centre \(O_1\) est à l’intérieur du cercle unité et les points de la parabole sont à l’extérieur.
Par contre, dans l’illustration suivante, le second centre \(O_{2e}\) du KE-cercle parabole étant à l’extérieur du cercle unité, il existe des configurations où, non seulement \(O_{2e}\) est toujours centre du KH-cercle parabole, symétrique du premier dans la symétrie euclidienne d’axe \((O_{2e}O_{cu})\) (les trois premières lignes de calcul des longueurs), avec les KH-médiatrices du triangle \(A_{2h}B_{2h}C_{2h}\) concourantes en un autre KH-centre de cercle circonscrit, le point \(O_{2h}\), dont on illustre qu’il est « à même distance » des trois points du triangle (les trois dernières ligne de calculs de longueurs). On ne l’a pas construit pour ne pas alourdir la figure, mais le KH-cercle circonscrit associé n’est plus la parabole bleue. Pour le construire, il suffirait de prendre les KH-symétriques par rapport à \(O_{2h}\) des sommets du triangle \(A_{2h}B_{2h}C_{2h}\), et construire la conique passant par ces trois points symétriques et leurs trois points antécédents.
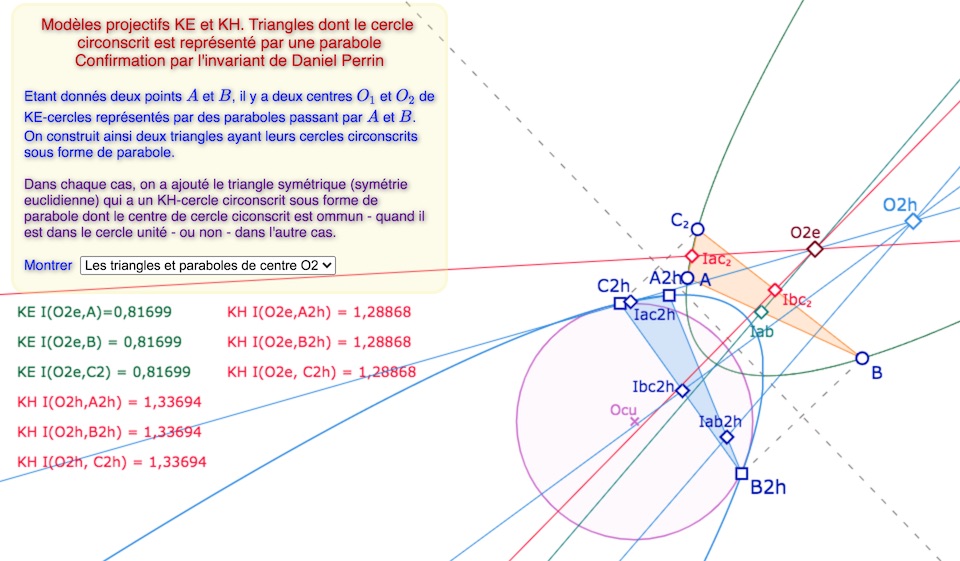
Lancer la figure associée dans un nouvel onglet pour différentes explorations.
Deux résultats intermédiaires (préliminaires)
Daniel Perrin s’amuse à associer quelques uns de ses résultats à des noms bien connus
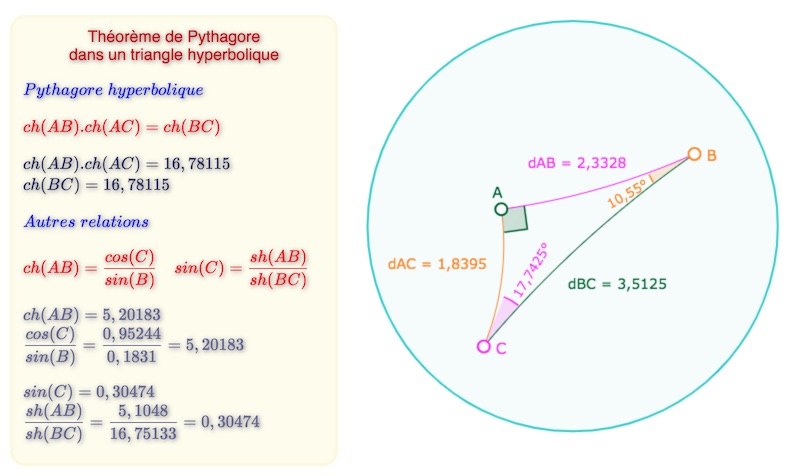
Nous énonçons maintenant un analogue non euclidien du théorème de Pythagore. Le lecteur ne s’étonnera pas d’en trouver une variante multiplicative. […]
Daniel Perrin – Partie 4 – p 145
Inutile de dire que Pythagore n’est pour rien dans ce résultat, mais je n’hésiterai jamais à affubler les théorèmes de noms évocateurs.
Théorème de Pythagore
Soient \(A, B, C\) trois points non isotropes, On suppose le triangle rectangle en \(A\).
Alors \(I(B,C) = I(A,B) \times I(A,C)\)
Manipulation d’une figure associée
On peut agir sur les trois points \(A, B, C\), mais aussi déplacer le centre du cercle unité et son rayon.
Il n’y a pas de réciproque, sauf dans certaines conditions sur lesquelles on reviendra ultérieurement.
Lien avec d’autres articles du site
Un « autre » Pythagore hyperbolique a été présenté – dans le disque de Poincaré – (en fait le même bien entendu) à la fin de cet article sur le manuscrit de Bolyaï
Ouvrir la figure associée à cette illustration, pour manipulation, dans un nouvel onglet.
Invariant dans KH et birapport de KB – Formule de Laguerre
Lorsque l’on est dans le cas hyperbolique, l’invariant I(a, b) a une description simple en termes du birapport des points a, b et des points isotropes de la droite (ab). […]
Daniel Perrin – Partie 4 – page 146
De même, j’appelle cette relation formule de Laguerre, mais c’est seulement par analogie avec la formule euclidienne usuelle. On ne prête qu’aux riches.
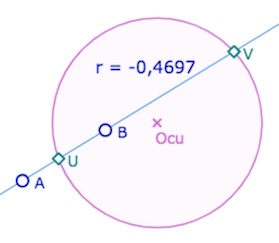
On rappelle que Daniel Perrin parle du « cas hyperbolique » quand la droite \((AB)\) coupe le cercle unité. Alors la partie intérieure au cercle peut être interprétée dans le contexte du modèle de Klein-Beltrami. On s’intéresse au birapport \(\displaystyle r_{AB} = \frac{\overline{AU}}{\overline{AV}} : \frac{\overline{BU}}{\overline{BV}}\).
Alors (Formule de Laguerre) \(4 \, I(A,B) = \displaystyle r_{AB} + \frac{1}{r_{AB}}+2\)
On peut déplacer les deux points \(A\) ou \(B\), ou encore le centre du cercle unité.
Le rapport est recalculé à chaque manipulation
De l’invariant I à la distance
S’agissant de la transitivité sur les couples de points a,b, l’invariant I donne naissance, dans les géométries réelles, à une “vraie” distance d(a, b),avec des formules presque identiques dans les deux cas. Précisément, si l’on pose d = d(a, b) et I = I(a, b), la formule qui lie la distance d et l’invariant I est I = cos2 d dans le cas elliptique et I = ch2 d dans le cas hyperbolique.
Daniel Perrin – Partie 4 – page 176
En pratique, il n’y a aucun problème dans KE. Par contre, dans KH, on se limitera aux points à l’intérieur du disque unité – le modèle KB – pour une cohérence interne, même si l’expression de cette distance conserve du sens pour deux points \(A\) et \(B\) extérieurs au cercle unité si la droite \((AB)\) coupe le cercle unité.
On a donc, dans KE, \(d(A,B) = cos^{-1}\left(\sqrt{I(A,B)}\right)\), et
dans KH, \(d(A,B) =argch \left(\sqrt{I(A,B)}\right) = ln \left( \sqrt{I(A,B)}+\sqrt{I(A,B)-1} \right)\).
Illustrations sur une figure dynamique
On reprend la même figure que celle de la présentation de l’invariant, mais avec ces nouvelles distances. Les trois points \(M, N, P\) sont toujours aimantés par la droite \((AB)\) et par tous les points de la figures. La distance dans KE est exprimée en degrés.
Utilisation dans KE
• Par exemple en plaçant \(M\) sur le KE-pôle de \((AB)\) et \(N\) sur la droite \((AB)\), alors \(d(M,N) =90\). C’est la distance maximale de deux points de KE.
• Comment placer \(M, N, P\) pour que les trois mesures soient à 90 (triangle tripolaire) ?
De nombreuses situations sont à tester en dehors de celles proposées
.Utilisation dans KH
• Le sens de la distance dans KH . Dans la configuration de l’ouverture – on peut relancer la figure avec l’icone de l’iframe – on peut placer un point sur \(A\), un sur \(B\) et le troisième sur \(I_{kh}\), alors les trois distances existent et \(I_{kh}\) est à même distance des deux points. Mais si on place \(B\) de l’autre côté du cercle, tel que la droite coupe le cercle, \(I_{kh}\) étant dans le cercle, la notion de milieu continue d’exister, au sens donné dans la page d’introduction, et celle de l’invariant précédent, mais pas en terme de distance.
• Tester quand les deux points \(A\) et \(B\) sont à l’intérieur du cercle unité. On est dans le modèle KB, il n’y a donc qu’un seul milieu au sens de la distance : \(I_{kh}\).
• Comment placer les trois points \(M, N, P\) pour qu’un point soit le milieu des deux autres aussi bien dans KE que KH comme ci-dessous ?

Préférer ouvrir cette figure dans un nouvel onglet
Relation avec la distance de Cayley
La « formule la Laguerre » ci-dessus permet de montrer (p. 180-181) que, dans KB, la formule de la distance obtenue par l’invariant, basé sur la forme quadratique initiale est la même que la formule de Cayley présentée pour le cercle de KB. On a donc, en notant toujours \(r_{AB}\) le birapport :
\(d(A,B) =argch \left(\sqrt{I(A,B)}\right) =\displaystyle \frac{1}{2} \mid ln(r_{AB}) \mid \, = \, \frac{1}{2} \mid ln(r_{AB}^{-1})\mid \)
Daniel Perrin avait annoncé cela dès ses premières pages d’introduction en ces termes, dans la dernière phrase de cette citation :
Nous entrons dans le vif du sujet. Attention, par rapport aux textes standard sur les géométries non euclidiennes, ce livre présente une singularité. En effet, les points et les droites que nous définissons ici ne vérifient pas toujours l’axiome de base de la géométrie d’Euclide : par deux points passe une droite et une seule. Il nous semble, en effet, qu’il est préférable de renoncer à cet axiome dans un premier temps, même si le poids des traditions s’y oppose. Cette généralisation ne concerne d’ailleurs que le cas hyperbolique pour lequel elle revient à ajouter aux points du disque de Klein les points extérieurs. Dans ce cas, on verra que le surcroît d’efficacité obtenu en utilisant la polarité vaut bien quelques concessions. On verra tout au long des chapitres suivants qu’on retrouve aisément les résultats usuels en spécialisant les résultats généraux aux points et droites hyperboliques.
Daniel Perrin – Partie 4 – page 22 (le disque de Klein est ce que l’on nomme le « modèle KB » ici)
L’approche de Daniel Perrin est donc un autre point de vue, plus large que l’approche classique, centré sur la cohérence de traiter en même temps les deux géométries, elliptique et hyperbolique, car toutes les deux basées sur une forme quadratique non dégénérée – contrairement au cas euclidien – qui aboutit aux mêmes – ou présente autrement les résultats de Klein … puisque c’est son fil d’Ariane.
Il y a beaucoup plus de résultats dans son traité, dont Al-Kashi non euclidien, mais aussi le spin d’un triangle, notion dont il est l’auteur, très utile dans le cas elliptique. A part le spin, et les formules de trigonométrie, les principaux autres résultats ont déjà été illustrés dans les pages du menu ELL de ce site, dans le modèle usuel de la sphère projetée sur le plan. Nous les reprendrons dans le cadre de ces nouveaux modèles.
Angles de droites
Dans cette section aussi, nous allons retrouver, avec son approche, les mêmes résultats – et les mêmes formules – que dans les pages traitant plus classiquement de la géométrie elliptique, dans le cadre plus large de tout le plan elliptique : le modèle KE.
Un invariant pour les droites
Daniel Perrin propose un invariant sur les droites, \(I^*(d_1, d_2)\), comme il l’a proposé sur les points. C’est (un prélude à) la notion d’angle de droites. Même si ce n’est pas sa définition, une propriété équivalente à la définition de cet invariant est le résultat suivant :
Soient \(d_1\) et \(d_2\) deux droites non isotropes, \(P_1\) et \(P_2\) leurs pôles respectifs. Alors \(I^*(d_1, d_2) = I(P_1, P_2)\).
Autrement dit, l’angle de deux droites est la « distance » entre leurs pôles.
Ce qui précède est une nouvelle illustration de la puissance de la polarité. Toute assertion concernant les longueurs aura désormais une traduction en termes d’angles et réciproquement.
Daniel Perrin – Partie 4 – page 150
Il en résulte que (conséquences immédiates) :
• Deux droites sont perpendiculaires ssi leur invariant est nul
• L’invariant de deux droites est égal à 1 si elles sont confondues ou si elles se coupent en un point isotrope (autrement dit sont parallèles pour KB).
Les valeurs numériques de \(I^*(d_1, d_2)\) (pour deux droites non isotropes)
Dans KE, on a toujours \(0 \le I^*(d_1, d_2) \le 1\).
Dans KH, comme pour l’invariant des longueurs dont c’est un dual, il y a plusieurs cas
• Si \(d_1\) et \(d_2\) sont toutes deux extérieures au cercle unité, on a \(I^*(d_1, d_2) \ge 1\),
• Si une des deux droites coupe le cercle unité et pas l’autre, on a \(I^*(d_1, d_2) \le 0\),
• Si les deux droites se coupent à l’intérieur du cercle unité, on a \(0 \le I^*(d_1, d_2) \le 1\),
• Si les deux droites se coupent sur le cercle unité, \(I^*(d_1, d_2)= 1\),
• Si les deux droites coupent le cercle unité, et sont sécantes en dehors, on a \(I^*(d_1, d_2)> 1\).
Illustration dynamique
Dans la figure suivante on s’intéresse à l’invariant (pour KE et KH) des deux droites \((AB)\) et \((BC)\). On a construit les KH pôles \(KHp_{AB} \, KHp_{BC}\)et les KE pôles \(KEp_{AB} \, KEp_{BC}\) de ces deux droites. On a tracé
• La droite – rouge – \((B\, KHp_{AB})\), la KH-perpendiculaire à \((AB)\) passant par \(B\).
• La droite – orange – \((B\, KHp_{BC})\), la KH-perpendiculaire à \((BC)\) passant par \(B\).
• La droite – vert foncé – \((B\, KEp_{AB})\), la KE-perpendiculaire à \((AB)\) passant par \(B\).
• La droite – vert clair – \((B\, KEp_{BC})\), la KE-perpendiculaire à \((BC)\) passant par \(B\).
Utilisation de la figure : Le point \(C\) est aimanté par les deux droites passant par \(KHp_{AB}\) ou \(KEp_{AB}\), pour tester l’invariant de deux droites orthogonales.
De même \(A\) est aimanté par les deux droites passant par \(KHp_{BC}\) ou \(KEp_{BC}\).
Enfin, le point \(B\) est aimanté par le cercle unité pour tester le cas des droites KB-parallèles.
Placer aussi le point \(B\) à l’intérieur du cercle unité, pour tester l’un des différents cas détaillés plus haut.
Préférer ouvrir cette figure dans un nouvel onglet
Angle de droites
Dans le cas elliptique comme dans le cas hyperbolique où les droites \(d_1\) et \(d_2\) se coupent à l’intérieur du cercle unité (dans le modèle KB donc), on pose :
\(I^*(d_1, d_2) = cos^2 \theta\), avec \(\displaystyle \theta \in \left[ 0, \frac{\pi}{2} \right]\).
\(\theta\) est l’angle non orienté des droites \(d_1\) et \(d_2\).
On reprend la figure précédente avec les mêmes aimantations sur les mêmes droites. On a calculé les trois angles de droites du triangle \(ABC\) et la somme des angles. Pour que les trois angles existent pour KH, il faut que les trois points soient dans le cercle unité.
Préférer lancer cette figure dans un nouvel onglet.
On sait que la somme des angles d’un triangle elliptique est toujours supérieure à 180°, et pourtant on remarquera que, dans certaines configurations ce n’est pas le cas : il suffit de rendre un angle obtus pour que la propriété ne soit pas vérifiée : c’est la définition de l’angle de droites qui n’est pas suffisante, il faut arriver à définir les angles de demi-droites.
Même si c’est nettement plus technique et que l’on consacrera des pages aux triangles de KE et KH, comme c’est un peu dommage de terminer sur celle figure, on poursuit un peu plus loin, comme teaser d’un futur article sur les triangles, par les angles de demi-droites.
Angles de demi-droites
On a retenu comme « définition » de \(I^*\) de deux droites la propriété que c’est (aussi) l’invariant de leurs pôles. C’est une définition élémentaire, tout de suite opérationnelle d’un point de vue des constructions géométriques. Mais pour passer aux demi-droites il faut adopter une approche plus calculatoire, essentiellement pour retrouver un signe initial. Une définition équivalente, avec le vocabulaire et les notations de Daniel Perrin, s’écrit (voir page 197 et surtout page 151 pour les détails)
\(\displaystyle I^* \left( (AB),(AC) \right) = \frac{\varphi(A \wedge B, \, C \wedge A)^2}{q(A \wedge B) \, q(C \wedge A)}\)
avec \(q(A \wedge B) = q(A)q(B)- \varphi(A,B)^2\) et
\(\varphi(A \wedge B, A \wedge C) = q(A) \varphi(B,C) – \varphi(A,B) \varphi(A,C)\)
Les formules valent pour KE. Pour KH, il faut changer de signe. En pratique pour le prochain calcul de \(I^+\), il suffira de changer de signe, pour KH, seulement le numérateur, à cause de la valeur absolue.
Notre objectif ici est d’en donner une variante en termes de demi-droites, ce qui revient essentiellement à préciser les signes dans cette formule.
Daniel Perrin – Partie 4 – page 197
Pour cela, on prend la « racine carrée » de l’invariant précédent, en conservant le signe de de la forme polaire \(\varphi\), soit (à quelques précisions d’utilisation que l’on ne détaille pas ici) :
Pour trois points \(A, B, C\) non isotropes du plan KE ou KH, tel que \(A\) ne soit orthogonal si à \(B\) ni à \(C\), on défini l’invariant des demi-droites d’origine \(A\) par
\(\displaystyle I^{+} \left( [AB), [AC) \right) = \frac{\varphi(A \wedge B, A \wedge C)}{\sqrt{\mid q(A \wedge B) \, q(A \wedge C) \mid}}\)
La valeur absolue ne sert que pour KH bien entendu … et on n’a pas défini la notion de « demi-droite », ce qui serait nécessaire pour KE, et sera fait au prochaine article d’où le contexte de « teaser » de cette dernière partie de l’article.
Angle de demi-droites
On a \(I^+([AB),[AC)) \in [-1,1]\).
L’angle non orienté des demi-droites \([AB)\) et \([AC)\) est, par définition le nombre \(\theta = cos^{-1} \left(I^+([AB),[AC)) \right)\).
C’est un élément de \([0, \pi]\) : on retrouve donc nos angles obtus dont les angles de droites ne rendaient pas compte.
Figure dans KE
On vérifiera que quand l’invariant des demi-droites est négatif, l’angle des demi-droites associé
est le supplémentaire de l’angle de droite correspondant.
Préférer ouvrir cette figure KE dans un nouvel onglet.
Figure dans KH
Mêmes remarques qu’à la figure précédente. Dans les deux cas \(B\) est légèrement aimanté par la droite \((AC)\).
Il peut falloir parfois bouger un peu le point \(B\) pour que les calculs s’affichent complets comme ci-dessous dans KH :
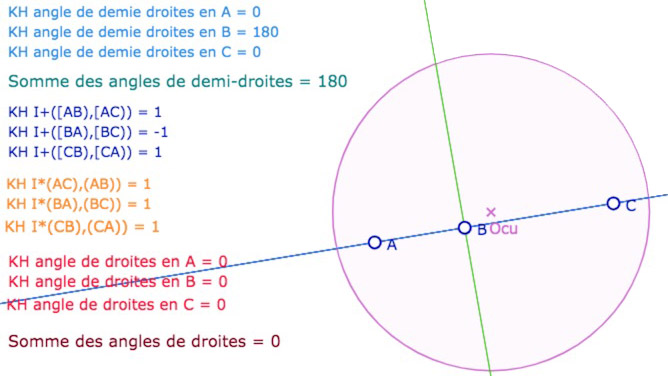
Ce qui valide aussi des propriétés angulaires d’alignement dont on reparlera ultérieurement.
Préférer ouvrir cette figure KH dans un nouvel onglet
Les prochains articles sur KE et KH reviendront sur les triangles (Spin et Al-Kashi pour le 4 ci-dessous), les segments et d’autres sur les cercles.
Les modèles projectifs KE et KH – 1 – les droites | KE KH – 2a – Cercles
KE KH – 2b – les « cercles-paraboles » | KEKH – 4 – Spin d’un triangle