Dans cet article on fait un petit écart sur les cercles de KE et KH en s’intéressant uniquement au cas où ils qui sont représentés par une parabole.
On a déjà réalisé une construction algébrique, donc très efficace, de cette situation dans la page d’introduction aux cercles. Efficace pour un tracé minimaliste mais moins pour l’aimantation d’un point
Rappel de la construction précédente
Dans une première partie, on se propose de reprendre le cas de la parabole d’une manière uniquement géométrique. C’est en particulier utile – et a déjà été utilisé dans l’article précédent sur les cercles – pour le cas où on a besoin d’une aimantation sur cette parabole qui va être construite par un lieu.
Puis, dans une seconde partie, on s’intéresse aux triangles dont le cercle circonscrit est représenté par une parabole.
Approche géométrique
du « cercle-parabole »
Un premier cas particulier – obtenu par construction affine
C’est le cas le plus simple : dans KH, avec la conique tangente au cercle unité quand \(O\) est extérieur au cercle unité. On a donc deux points de contact de la conique (ci-dessous \(U_1\) et \(U_2\)) avec ses tangentes en \(O\). On a donc 4 contraintes affines – sur 5 pour déterminer la conique. Si donc on se donne une contrainte supplémentaire – par exemple « passe par \(A\) » – la conique cherchée est entièrement déterminée. Or on sait que si la contrainte est que ce point \(A\) est le milieu de \([IO]\) alors la conique est une parabole.
Rappel de la construction affine de la parabole passant par les deux points de contact \(U_1\) et \(U_2\) et ses tangentes sécantes en \(O\). On construit \(S\) milieu de \(I\) et \(O\). Alors \(S\) est un point de la parabole, et on itère le procédé : la tangente en \(S\) est la parallèle à \((U_1U_2)\). Elle coupe les tangentes précédentes en \(T_1\) et \(T_2\). Soient \(I_1\) et \(I_2\) les milieux de \([SU_1]\) et \([SU_2]\), puis \(V_1\) et \(V_2\) les milieux de \([I_1T_1]\) et \([I_2T_2]\). Alors, la conique passant par \(U_1,\; V_2,\, S,\, V_1\) , et \(U_2\) est une parabole – ici de plus de sommet \(S\).
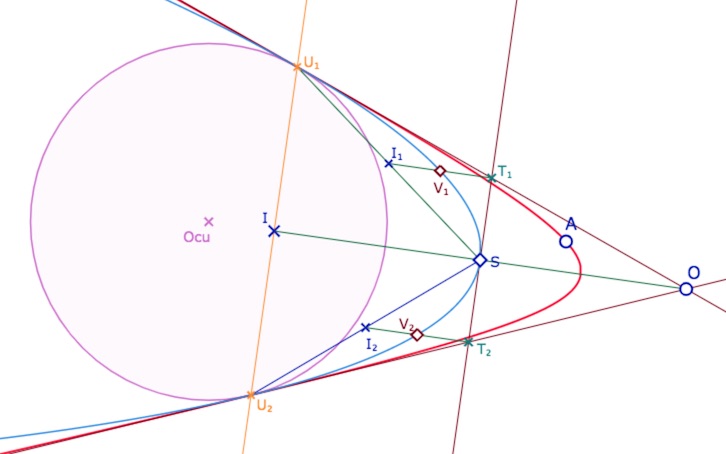
Construction du cercle –« parabole » bitangente au cercle unité, donc de KH.
En pratique c’est le cercle passant par \(S\), le milieu de \(I\) et \(O\) .
On a compris aussi que, comme c’est « encore » une conique, ce n’est pas vraiment cela que l’on cherche.
Un second cas, commun à KE et KH, issu d’une construction projective
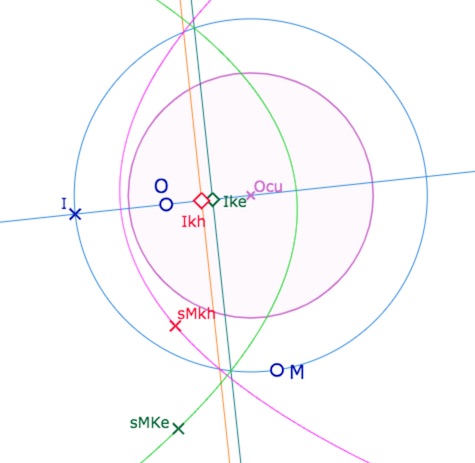
On place le point \(O\), centre du cercle cherché, à l’intérieur du cercle unité. On nomme \(I\) l’inverse de \(O\) par rapport au cercle unité. On considère alors les milieux \(I_{kh}\) et \(J_{kh}\), de KH, de \(O\) et \(O_{cu}\) le centre du cercle unité. Ces milieux existent car les deux points sont tous les deux à l’intérieur du cercle unité. Puis on construit les milieux \(I_{ke}\) et \(J_{ke}\), de KE, des deux mêmes points \(O\) et \(O_{cu}\). Ces deux points, eux, existent toujours, que \(O\) soit intérieur ou non au cercle unité. On construit ensuite les perpendiculaires euclidiennes passant par \(I_{kh}\) et \(I_{ke}\) à \((OO_{cu})\)car elles sont aussi des perpendiculaires pour KE et KH puisque passant par le centre du cercle unité. Ces deux droites sont donc médiatrices dans KH et KE du centre \(O\) du cercle cherché et du cercle de centre \(O_{cu}\) passant par \(I\).
Le lieu du symétrique d’un point \(M\) sur ce cercle par rapport aux médiatrices précédentes de KE et KH – les points \(sM_{kh}\) et \(sM_{ke}\) dans l’illustration précédente, sont dans chaque géométrie, l’unique cercle de centre \(O\) représenté par une parabole.
Pourquoi cette conique est-elle une parabole ?
Le symétrique par rapport à la médiatrice (verte dans l’illustration ci-dessous) du cercle de centre \(O_{cu}\) passant par \(I\) est un cercle (dans l’illustration un KE-cercle) de centre l’image de \(O_{cu}\), le point \(O\), de sommet – sur l’axe \((OO_{cu})\) – l’image du point \(I\) et de second sommet l’image de \(J\). Or \(J\) est le milieu euclidien des deux KE-milieux \(I_{ke}\) et \(J_{ke}\) et donc l’image de ce point est à l’infini (on rappelle que l’image de \(M\), le point \(sM_{ke}\) est, par construction le 4° point de la division harmonique \(J_{ke}\), \(M_p\) et \(M\), le milieu étant alors renvoyé à l’infini). Autrement dit le second sommet de cette conique est à l’infini, ce qui signifie que la conique est une parabole (tangente à la droite de l’infini).
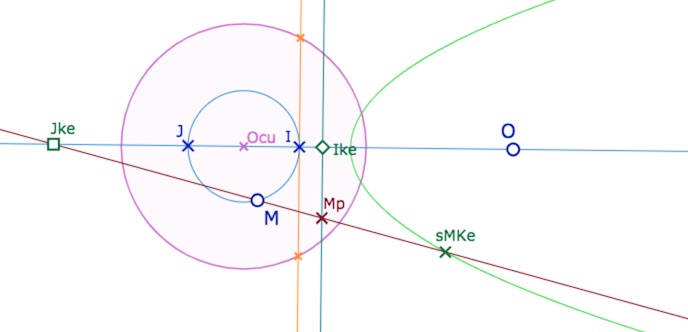
Pour le régionnement du plan vis à vis du type de conique obtenue pour le cercle de centre \(O\) passant par \(A\), on peut ajouter la parabole construite de manière affine dans cette figure pour avoir aussi une parabole dans KH pour \(O\) extérieur au cercle unité.
Tester les cas, dans chaque géométrie, le cas \(O\) dans ou à l’extérieur du cercle unité
Rappel : on peut déplacer aussi le centre du cercle unité et le rayon du cercle unité, en tirant dessus.
Préférer lancer la figure dans un nouvel onglet.
On retrouve, dans ces constructions, que les KE et KH cercles-parabole sont symétriques par rapport à la médiatrice de leur centre \(O\) et du centre du cercle unité \(O_{cu}\).
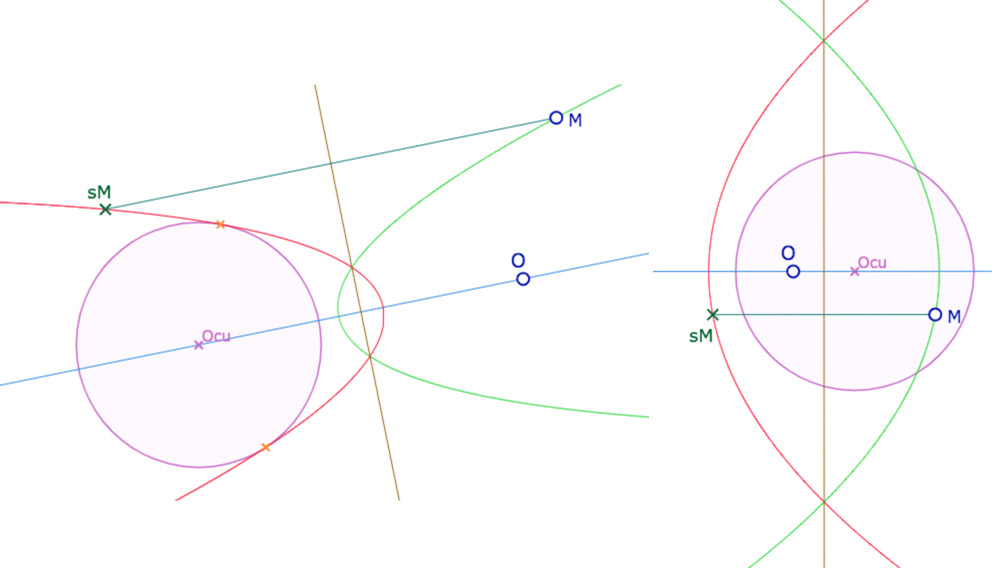
Et c’est en particulier cette construction – par deux lieux – que l’on retient pour les aimantations. On a donc, à notre disposition, deux macros, dans KE et dans KH, pour une parabole algébrique – avec peu d’objets, et une autre par lieu, un peu plus longue.
Construction d’un triangle ayant une parabole
comme KE-cercle circonscrit
Ce qui suit dans la suite de l’article est une exploration dynamique empirique – correcte certes, et partiellement argumentée, mais certaines constructions sont basées sur des conjectures qui nécessitent une preuve mathématique.
Lieu des centres O des KE-cercles passant par A représentés par une parabole
On inverse le questionnement précédent : étant donné un point \(A\), quel est le lieu des centres \(O\) des cercles passant par \(A\) qui est représenté par une parabole ?
On se donne un point \(A\) du plan. On conjecture que le lieu cherché est une conique. Comme c’est clairement un lieu borné, on cherche une ellipse, plus précisément une ellipse de centre \(A\). Explorons cela dans la figure suivante.
La KE-médiatrice « affinement intérieure » de \(A\) et du centre \(O_{cu} \)coupe le cercle unité en 2 points \(E_1\) et \(E_2\). Ces deux points appartiennent à l’ellipse cherchée (voir manipulation proposée ci-dessous, ce serait le principal résultat à montrer, le reste en découlant). Comme la conique est centrée en \(A\), elle passe aussi par leurs symétriques euclidiens \(sE_1\) et \(sE_2\). On a donc 4 points de l’ellipse. Reste un cinquième point à préciser. En pratique on en a deux autres car la médiatrice est aussi KE-axe de symétrie de la conique, donc on peut prendre les KE-symétriques ce sont les points \(s_sE_1e\) et \(s_sE_2e\). On a six points, la conique passant par 5 de ces points passe par le sixième point.
Manipulations proposées :
• On a construit l’unique KE-cercle « parabole » (en orange) de centre \(U\) appartenant au cercle unité. Déplacer \(U\) pour voir que les deux intersections de la médiatrice et du cercle unité sont les seule points du cercle pour lesquels la parabole passe par \(A\). En fait c’est le principal résultat à démontrer,: pourquoi le cercle de cente \(E_2\) passant par \(A\) est-il représenté par une parabole ?. A ce stade, il manque une caractérisation sur les « cercles parabole ».
• \(O\) est un point de l’ellipse, on construit le KE-cercle « parabole (vert clair) avec la macro usuelle – donc indépendant du point \(A\). On vérifie que le cercle-parabole passe bien par \(A\).
Préférer ouvrir cette figure dans un nouvel onglet
Dans cette figure – celle ouverte « dans un nouvel onglet « – le lecteur qui a l’habitude d’utiliser les macros peut prendre la macro KE SymO CU M Drt du dossier KE, pour construire le KE-symétrique de \(O\) par rapport à la médiatrice, et vérifier visuellement que cette droite est axe de symétrie de la conique.
Construction d’un triangle ayant un KE-cercle circonscrit « parabole »
Cette figure étant réalisée, la construction d’un triangle dont le KE-cercle circonscrit est représenté par une parabole est immédiat à finaliser.
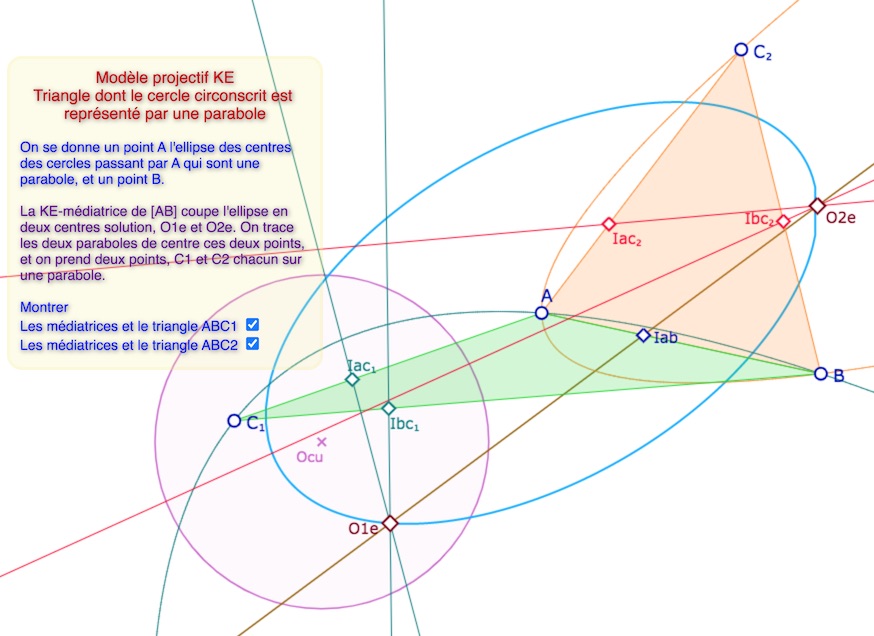
La figure est trop grande pour être ouverte dans cette page. Ouvrir la figure dans un nouvel onglet.
Manipulation proposée : déplacer \(A\), puis \(B\) ou les points \(C_1\) et \(C_2\) sur les deux paraboles.
Rappel : dans KE et KH un triangle admet 4 centres de cercles circonscrits qui sont les pôles des quatre droites des milieux, il y aurait donc matière à poursuivre cette exploration en ce sens. Nous en dirons un mot à la prochaine section.
KE et KH cercles circonscrits sous forme de paraboles
Comme les KE et KH cercles-parabole sont symétriques (dans une symétrie euclidienne), on peut en déduire la construction de triangles de KH qui admettent, à leur tour, un KH cercle circonscrit sous forme de parabole. C’est ce que l’on se propose d’explorer dans cette section.
Cas où le centre du cercle circonscrit est intérieur au cercle unité
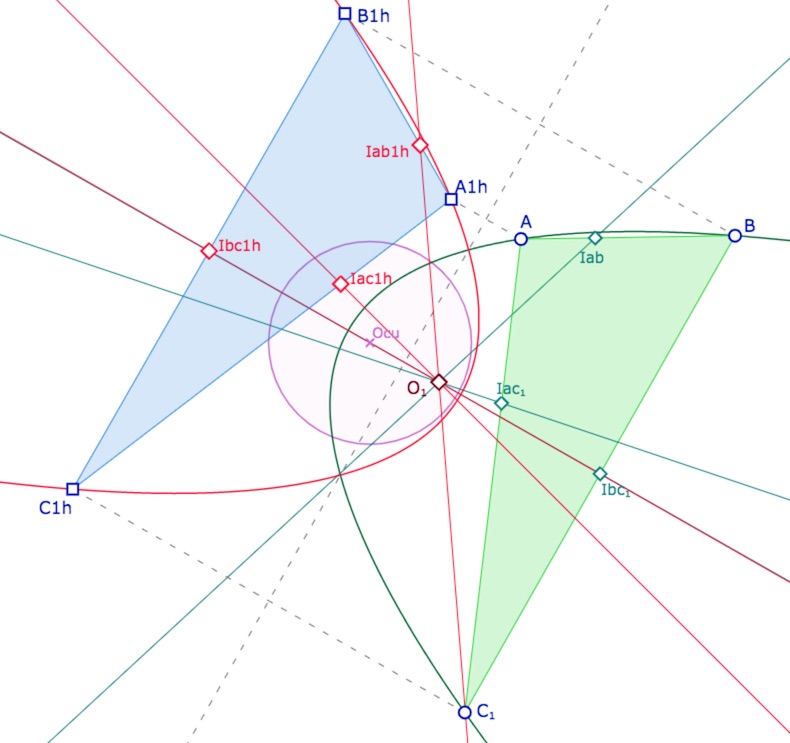
Depuis le triangle \(ABC_1\) de la figure précédente, sur la parabole de centre \(O_1\) (on a enlevé le \(e\) de \(O_{1e}\) car il est désormais commun à KE et KH) on construit le triangle symétrique, dans la symétrie euclidienne d’axe la médiatrice euclidienne de \([O_1O_{cu}]\), c’est le triangle \(A_{1h}B_{1h}C_{1h}\) et on complète par leurs KH symétriques de centre \(O_1\) pour avoir les points permettant de construire la parabole symétrique. On termine par les KH médiatrices du triangle : elles sont bien concourantes en le centre du cercle-parabole \(O_1\). Autre illustration de la même situation.
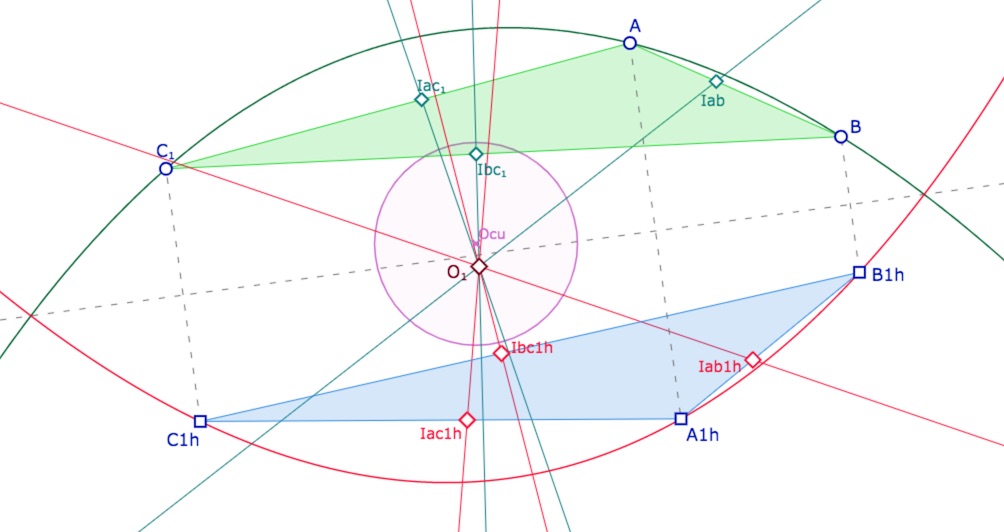
Dans la figure que l’on peut ouvrir un peu plus loin, chacun peut placer aussi les deux triangles \(ABC_1\) et \(ABC_2\) dans le cercle unité, comme ci-dessous. On a laissé la conique initiale « lieu des centres » des paraboles passant par \(A\).
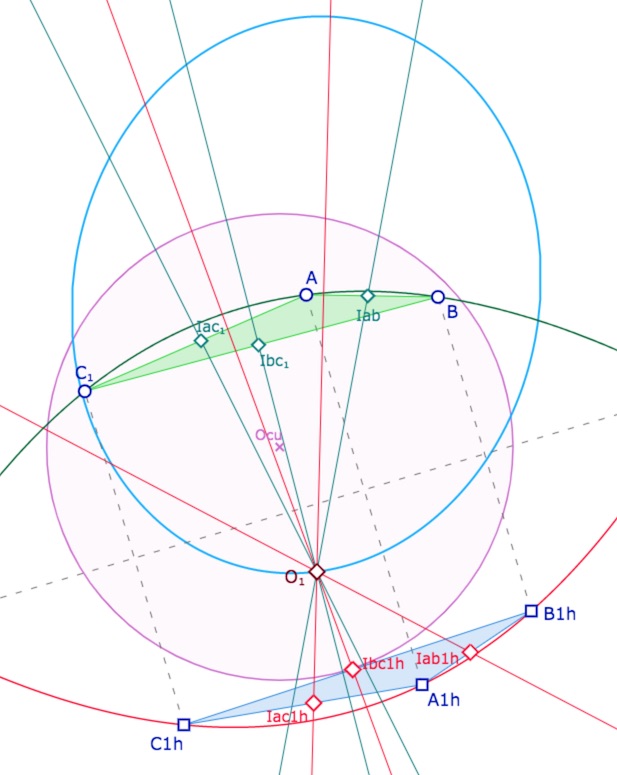
Ci-dessus avec \(ABC_1\), ci-dessous avec \(ABC_2\) à l’intérieur du cercle unité.
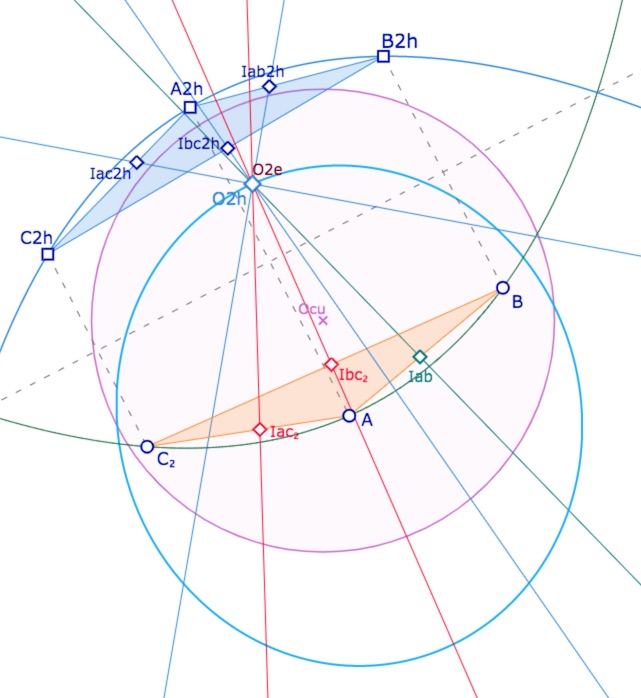
La figure est manipulable un peu plus loin car il est préférable de rendre compte d’une autre situation avant.
Cas où le centre des cercles-parabole est extérieur au cercle unité
On poursuit par une situation identique à la précédente, avec des notations adaptées. La parabole du KH-cercle a encore été construite à partir des symétriques euclidiens \(A_{2h}, B_{2h}, C_{2h}\) puis de leurs KH– symétriques par rapport au point \(O_{2e}\) centre de la seconde parabole de la figure précédente.
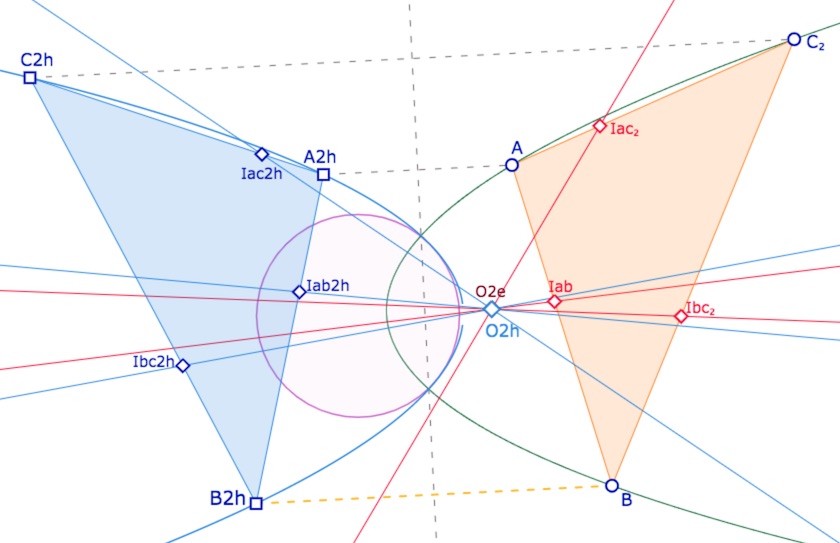
On remarque tout de suite que l’on a gardé le nom \(O_{2e}\) et construit l’intersection des KH-médiatrices qui se coupent en \(O_{2h}\). Dans cette illustration les deux centres \(O_{2e}\) et \(O_{2h}\) coïncident.
Mais cette situation n’est pas générale. Déplaçant les sommets \(A\) et \(B\) du triangle initial, on peut arriver, facilement, à ce type de situations où les KH-médiatrices du triangle \(A_{2h}B_{2h}C_{2h}\) sont bien concourantes, mais en un point \(O_{2h}\) différent de \(O_{2e}\), le centre du KH cercle-parabole, qui a été construit avec lui. De plus, pour le logiciel, les points \(Ibc_{2h}\), \(O_{2h}\) et \(O_{2e}\) sont alignés.
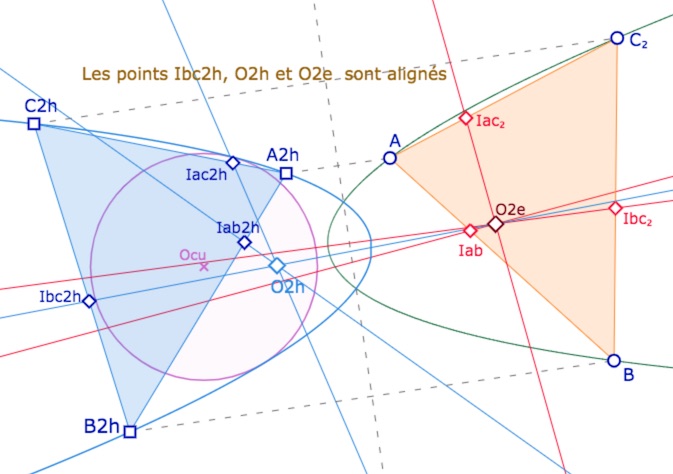
Ouvrir la figure générale de cette section dans un nouvel onglet
Remarque : dans les illustrations la médiatrice passant par \(Iab\) change de couleur dans les deux géométries mais ce n’est pas le cas dans la figure.
Les illustrations proposées dans la suite ne sont pas intégrées dans cette figure. Pour les lecteurs habitués au logiciel, on peut poursuivre soi-même, toutes les macros sont disponibles.
Cette propriété d’alignement est une piste pour expliquer ce résultat : en pratique, on est sur un des trois autres centres de cercle circonscrit du triangle \(A_{2h}B_{2h}C_{2h}\) dont on a rappelé l’existence un peu plus haut, il y a échange des médiatrices alors que l’on a privilégié, dans notre construction le point « affinement intérieur » à deux points … ce qui induit non pas en erreur, mais à tout le moins, une représentation mentale orientée …
Dans l’illustration suivante, on a ajouté deux des quatre droites des milieux (en rose), celles dont les pôles sont les deux centres des cercles circonscrits : Le point \(O_{2h}\) est le pôle de la droite passant par \(Jac_{2h}, \, Jbc_{2h}, \, Jab_{2h}\), la droite des milieux « affinement extérieurs » aux points concernés. Et \(O_{2e}\) est le pôle de la droite passant par \(Jac_{2h}, \, Ibc_{2h}, \, Iab_{2h}\).
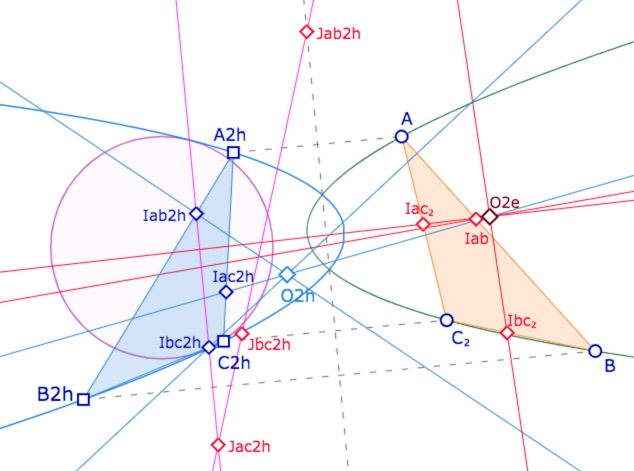
On notera que si \(O_{2h}\) est bien le centre d’un KH-cercle circonscrit à \(A_{2h}B_{2h}C_{2h}\), ce cercle circonscrit n’est plus représenté par une parabole, mais, par exemple comme ci-dessous, une ellipse (en vert).
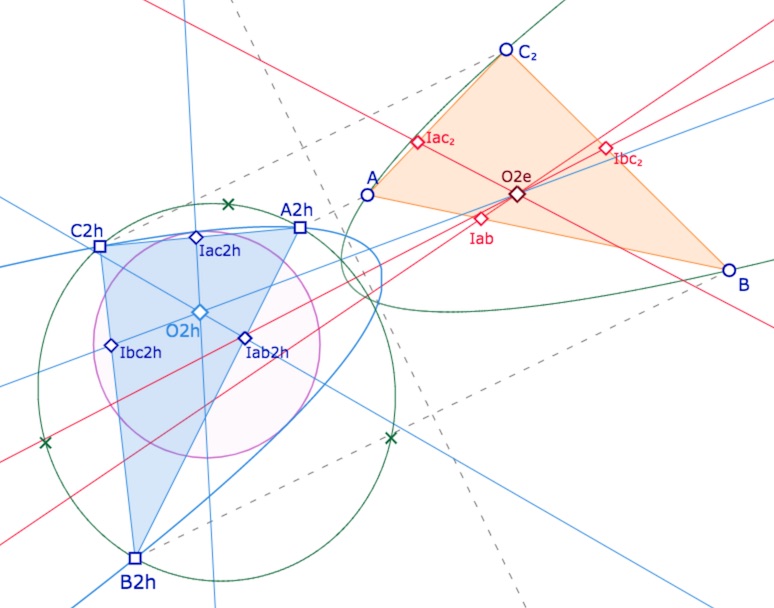
Ci-dessus \(O_{2h}\) avec le centre à l’intérieur du triangle, ci-dessous à l’extérieur.
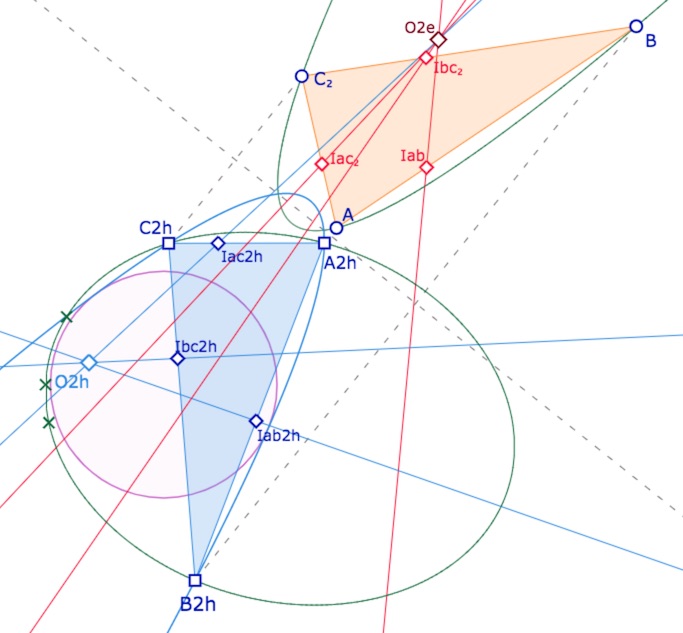
Clairement, comme ce cercle circonscrit peut aussi être représenté par une hyperbole, il existe des triangles pour lesquels c’est aussi une parabole. En attendant de chercher une construction qui permettrait d’obtenir cette troisième parabole, on peut facilement la simuler – mais ce n’est qu’une simulation. Ci-dessous, on a construit le KH-cercle de centre \(O_{2h}\) qui est une parabole (en rouge), puis on modifie \(B\) ou \(C_2\) pour que cette parabole coïncide avec le KH-cercle circonscrit au triangle \(A_{2h}B_{2h}C_{2h}\) (l’ellipse verte ci-dessus).
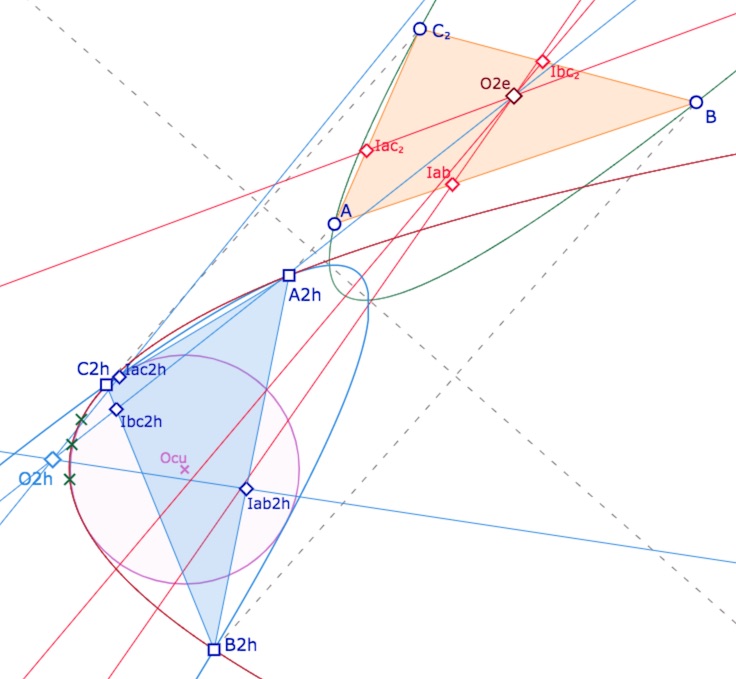
Ce serait intéressant de trouver une construction – par exemple de \(C_2\) – qui réaliserait cette troisième parabole comme cercle circonscrit. Cela demande d’en savoir plus sur des caractéristiques de ces cercles-parabole.
Autres approches dynamiques
envisagées pour la suite
Un des intérêts de la géométrie dynamique est d’aborder les configurations avec des approches très variées selon la façon dont sont construites les figures. On l’a déjà illustré dans plusieurs pages du menu Non Arg. Par exemple, dans de futurs articles, on envisage de construire des figures dont les paramètres importants de réalisation seront le centre du cercle unité et son rayon.
Même si la figure proposée est un peu caricaturale, voici un exemple simple toujours sur ce thème des KE-cercles-parabole. On cherche – sur un cas très particulier, d’où le côté caricatural – un triangle dont les trois cercles exinscrits sont des paraboles. Dans la figure suivante, on peut afficher ou cacher des cercles déjà construits, puis modifier le point \(A\) et surtout le rayon du cercle unité.
Les informations sont données dans la figure. On a vu dans l’article sur les droites que si une droite passe par le centre du cercles, les perpendiculaires euclidiennes sont aussi des perpendiculaires elliptiques, ce qui explique que la figure euclidienne est en grande partie aussi elliptique (dont même centres de cercles exinscrits)
Préférer lancer cette figure (sans les restrictions de l’iframe) dans un nouvel onglet
Dans cette figure (du nouvel onglet), les lecteurs habitués au logiciel peuvent modifier le rayon du cercle \(CU\) pour avoir les cercles-parabole effectivement tangents.
• Sélectionner la flèche de gauche (mode « création »), puis sur le cercle, activer l’icone « calculatrice », on entre alors en mode expression.
• Dans la partie expression en haut de la page, rentrer alors la valeur d(Ocu,A)*sqrt(2), comme exploré dans la figure ci-dessus.
• ne pas oublier de valider avec le bouton vert
• On peut alors déplacer \(A\), le rayon du cercle unité s’adapte pour que les cercles paraboles soient bien les cercles exinscrits.
Les modèles projectifs KE et KH – 1 – les droites | KE KH 2a Les cercles
KE KH – 3 – Longueur, distance et angles | KEKH – 4 – Spin d’un triangle