Réalisation des figures sur la pseudosphère (1/2 – Macros intrinsèques)

Dans le menu PS, nous avons vu deux approches pour réaliser des figures sur la pseudosphère :
• Des constructions par la géométrie intrinsèque de la surface (spécifique à la pseudosphère)
• Des constructions par conjugaison avec le modèle KB, du disque de Klein-Beltrami, comme on l’a déjà proposé pour la PSH.

Dans ce premier article, on s’intéresse aux constructions directement réalisées sur la pseudosphère.

Bien entendu, pour construire de telles figures, il faut avoir l’habitude d’utiliser les macros (rappel d’utilisation dans un contexte euclidien), et peut-être avoir déjà pratiqué avec des macros hyperboliques, par exemple dans KB (plus simple) comme proposé dans cet article ou celui sur les pavages dans KB.

Par ailleurs, même si on n’utilise que des expressions et des tracés automatiques, il est parfois préférable de renommer les noms des expressions (on va y revenir en détail) ou des points construits, donc avoir un peu l’habitude d’utiliser l’interface de DGPad.

Cet article est rédigé pour partager le plaisir de construire des figures sur la pseudosphère, sans technicité … et juste cela car toutes les figures proposées à la construction sont déjà téléchargeables dans le cours du menu PS. C’est donc essentiellement pour ouvrir un peu le capot de la pseudosphère et jouer avec le moteur.

Les sections de cette page

• La présentation des macros et de la figure initiale
• Utilisation des items de base (détails de la construction des médianes d’un triangle)
• Hauteurs et perpendiculaire commune
• Médiatrices et cercle circonscrit
• Médiatrices et équidistante (la figure la plus longue à réaliser)
• Illustration de la propriété « constante » de l’équidistante
• Horicycle par symétrie orthogonale (avec des illustrations originales)
• Présentation des macros disponibles mais non utilisées
• Une figure avec les points multifeuilles

Les macros de l’approche intrinsèque

Comme on l’a déjà mentionné dans le corps du menu PS, une partie importante des macro-constructions sont du calcul de coordonnées ou de constantes. Dans l’illustration ci-dessous, ce sont celles du dossier « Expressions« . Pour cet article, on a placé aussi placé plus de macros de « Dessin« , c’est à dire de tracés sur la pseudosphère qu’annoncé dans le menu PS. Le dossier « PS Base » ne sert qu’à ajouter des points sur la surface. A priori, il ne devrait pas être utilisé, sauf à vouloir réaliser des figures plus complexes.

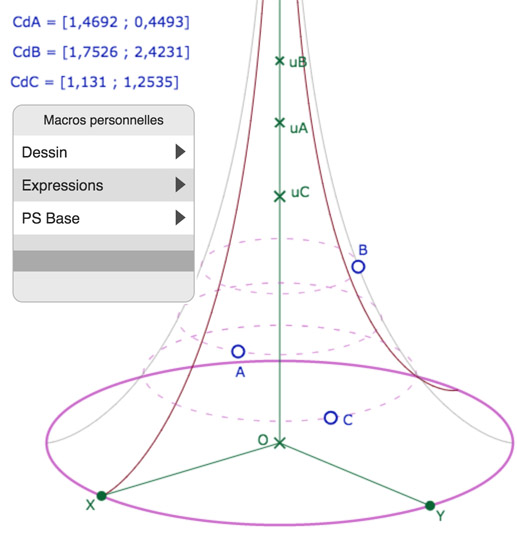
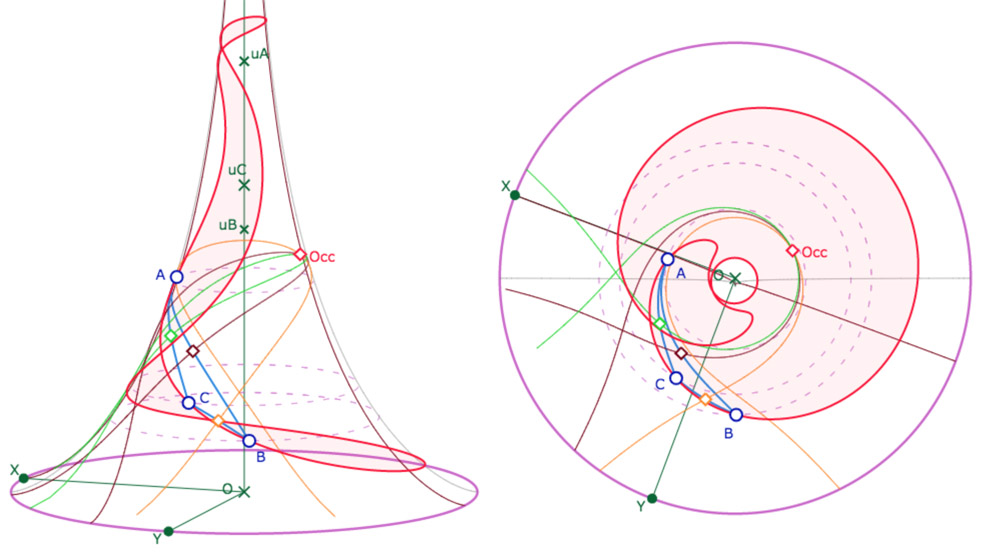
La figure de base, avec trois points sur la surface, et les coordonnées \([u, \theta]\) de ces trois points.
On y a ajouté le premier niveau des macros (qui n’apparaissent pas à cet endroit bien entendu).

Dans cette première figure initiale, les points sont sur la feuille principale. Celle-ci part du méridien passant par le point \(X\). En fin d’article on propose d’utiliser une figure avec les points de base pouvant être sur trois feuilles de la pseudosphère.

Vous pouvez lancer cette figure dans un nouvel onglet pour explorer les possibilités au fur et à mesure de leur description. Pour annuler une macro, on utilise la flèche retour à droite du tableau de bord, ou simplement relancer la figure en rafraichissant sa page. On peut lancer la figure plusieurs fois, dans plusieurs onglets pour garder les figures avant de les enregistrer.

Les macros des trois dossiers

En listant ces macros, on voit bien que l’on peut faire beaucoup de choses directement sur la pseudosphère. Il faut juste apprendre un peu à s’en servir.

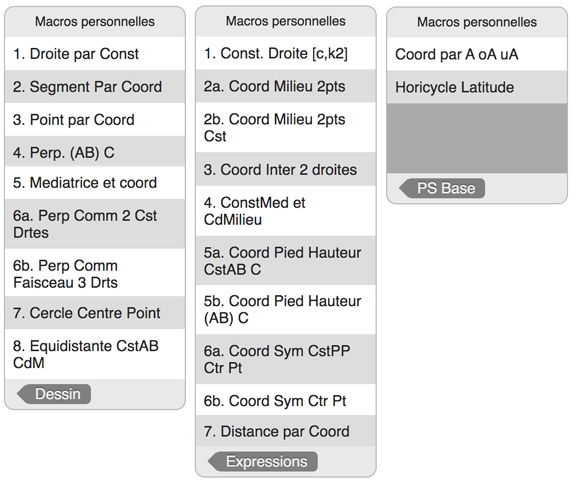
Sauf si on souhaite ajouter des points de base sur la pseudosphère (troisième dossier), pour toutes les autres macros les objets initiaux sont toujours des expressions, soit des coordonnées de points, soit des constantes de droites : on ne montre jamais de points pour ces constructions.

Enregistrement des figures

Cela se fait en deux clics. D’abord l’outil enregistrement (icone avant le nuage), puis cliquer sur le lien, et lui donner un nom. Il est conseillé d’y mettre tout de suite l’extension de DGPad, .dgp, même si cela reste un fichier texte.

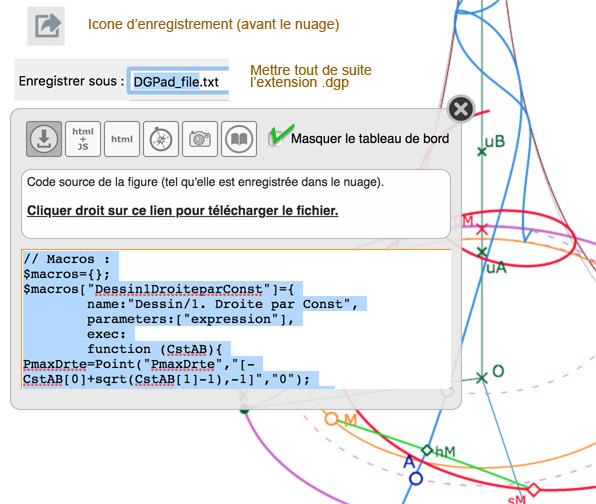
Pour lire à nouveau votre figure, il suffit de la glisser sur l’application en ligne de DGPad : https://www.dgpad.net/. On peut aussi télécharger une application de bureau dans l’un des trois principaux environnements (linux, windows, macOS).

Utilisation des items de base

Une première utilisation (segments, droites)

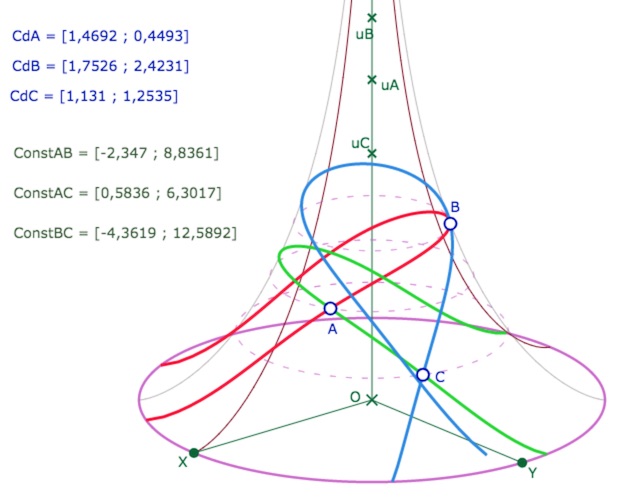
La seule construction que l’on puisse effectuer avec une seule macro est le tracé des côtés du triangle. En effet la macro Dessin 2 : Segment Par Coord ne demande que les deux expressions de coordonnées des points, déjà présentes dans la figure. Il est ainsi très simple de réaliser un triangle sur la pseudosphère, il suffit d’appliquer trois fois cette macro avec les coordonnées des points pris deux à deux.

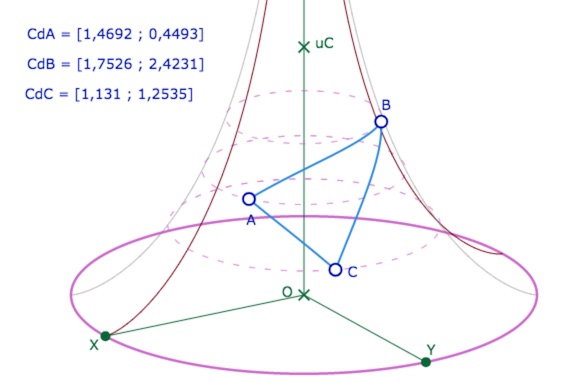
Pris de contact avec la pseudosphère. Désactiver les outils (mode consultation) pour pouvoir la tourner.
Explorer la vue de dessus en tirant la souris vers le bas.

Pour construire les droites supports des côtés du triangle, il faut d’abord « calculer » l’expression des constantes de la droite (Expression 1), puis ensuite construire la droite par ses constantes (Dessin 1). Les droites construites par les macros sont multifeuilles.

Gestion générale des expressions issues des macros

• Tout d’abord les expressions produites par une macro sont placées dans la page écran au même endroit. Si on utilise une macro plusieurs fois, Il faut donc déplacer les résultats pour qu’ils ne se superposent pas. Cela se fait directement dans le mode « macro » entre deux applications, simplement en tirant sur l’expression. Si on souhaite juste tracer les trois droites d’un triangle, il suffit de déplacer ces expressions à l’écran, et ensuite appliquer la macro Dessin 1 à chacune de ces trois expressions. On sera surpris que les constantes apparaissent avec le même « nom ». Mais en fait ce n ‘est pas leur nom, il s’agit de commentaires. On détaille cela au point suivant.
• En effet une expression, en dehors de sa valeur calculée, a deux paramètres, son nom de variable, utilisé dans l’enchainement des macros, géré automatiquement – même si on peut le modifier à tout moment – et le commentaire visible à l’écran. Ce commentaire est statique, c’est donc toujours le même dans une macro. Si on se lance dans une figure un peu chargée, il est utile de le modifier. Cela se fait ainsi, illustré sur le commentaire de la macro des constantes d’une droite :

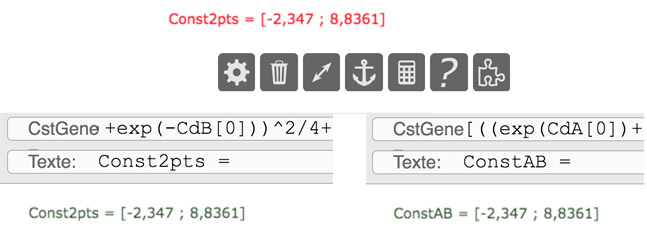
1. En mode standard (flèche gauche active), sélectionner l’expression, choisir le mode expression du logiciel par l’icone « calculatrice ».
2. L’expression s’ouvre (on voit son nom CstGene) et le commentaire texte. Placer la souris sur cette seconde ligne.
3. Et changer le nom par ConstAB par exemple. Ne pas oublier de valider par le bouton vert à droite.
4. Quitter le mode expression en repassant en mode standard et déplacer l’expression avant d’appliquer une nouvelle fois la macro.
   On peut aussi modifier toutes les expressions en même temps, on change d’expression après la validation de la modification.

Application de ce qui précède, en changeant la couleur des droites par l’inspecteur d’objets.
Rappel : il faut être en mode consultation (aucun outil sélectionné) pour tourner la pseudosphère.

Démarche pour la construction des médianes d’un triangle

Si on a réalisé la figure ci-dessus, il suffit de supprimer (icone corbeille et non pas gomme) les trois constantes des droites pour retrouver la figure initiale.

En étant un peu attentif, il suffit
• d’appliquer trois fois la macro Expression 2a des milieux par deux points – on montre les coordonnées des points. Déplacer le résultat à chaque fois,
• puis de construire les points sur la surface (facultatif) avec la macro Dessin 3, Point par coordonnées (les points sont nommés par cette macro, mais par défaut, le nom n’est pas affiché),
• et ensuite Dessin 2, Segment par Coordonnées en choisissant bien les points opposés aux milieux. Voici ce que cela donne, sans sophistication, avec le même commentaire pour les trois milieux :

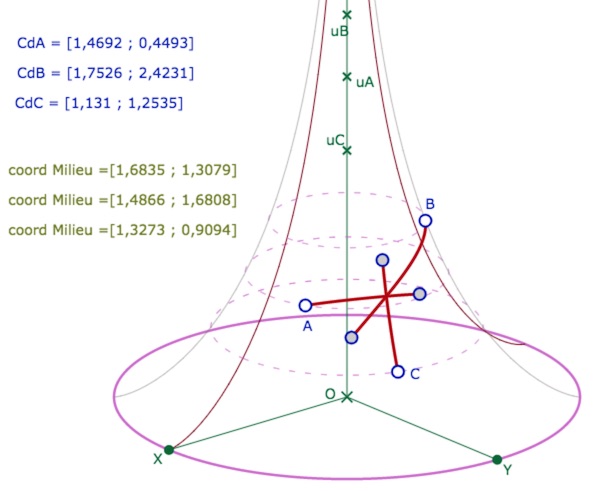
On voit bien que la première ligne « coord Milieu » correspond au milieu de \(A\) et [latex]B[/latex] car sa longitude (1,3) est un peut supérieure à celle de \(C\) (1,25). De même la deuxième ligne correspond au milieu de \(B\) et \(C\) car des trois c’est le point de plus grande longitude, et pour la troisième ligne, c’est au contraire celui de plus petite longitude, donc milieu de \(A\) et \(C\).

Bien entendu, on peut améliorer la réalisation comme ci-dessous. Cela demande juste une ou deux minutes.

Ajout du point de concours des médianes

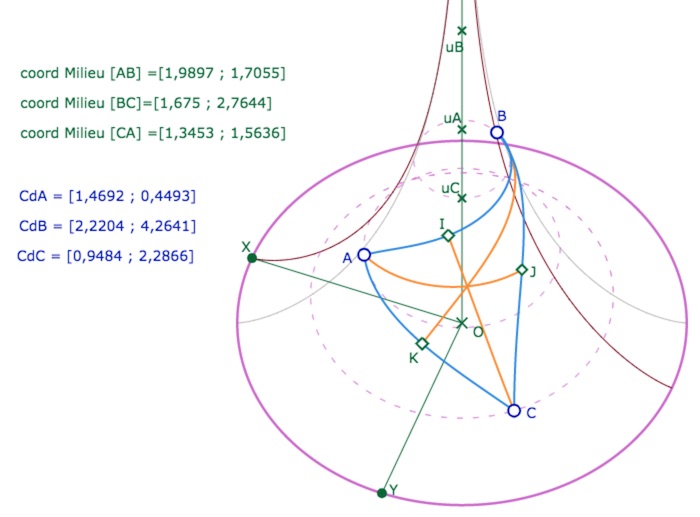
Il suffit de créer l’intersection de deux médianes. Pour cela il faut :
• Construire les constantes de deux médianes, en montrant les (coordonnées des) deux points par la macro Expressions 1.
• Construire ensuite les coordonnées de l’intersection des deux droites (macro Expressions 3)
• Tracer ce point sur la surface (macro Dessin 3) et éventuellement changer son aspect dans l’inspecteur d’objets.

Voici ce que cela donne, en version brute, sans modification des commentaires, en vue de dessus. On a renommé le point d’intersection.

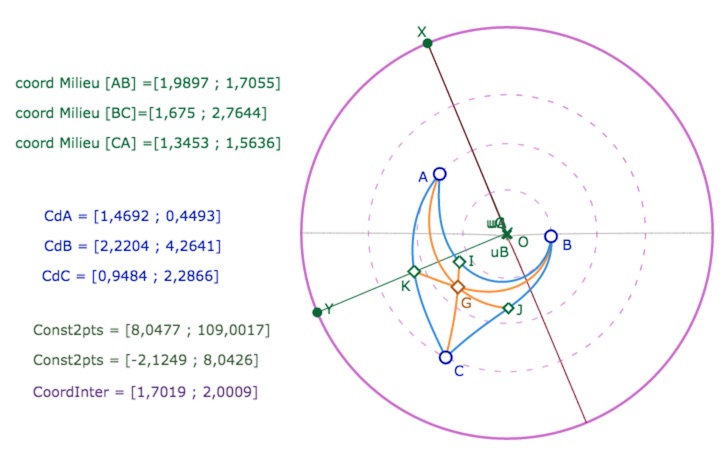
On remarque, dans cette illustration, que le milieu \(K\) est presque au dessus de \([OY]\),
ce qui est conforme à sa longitude (1,56 est proche de \(\pi/2\)).

Hauteurs et perpendiculaire commune

Si nécessaire relancer la figure de départ.

Pour les perpendiculaires, on dispose de plusieurs macros, selon la situation et ce que l’on veut en faire.
• Expressions 5a et 5b donnent les coordonnées du pied de la perpendiculaire sur une droite issue d’un point, selon que l’on ait les constantes de la droite ou (les coordonnées de) deux points de la droite. Cette macro sert plutôt pour construire des symétriques, quand on n’a pas besoin de construire la perpendiculaire elle-même.
• Dessin 4 : Perp (AB) C construit directement la perpendiculaire à une droite en donnant deux points \(A\) et \(B\) de la droites et le point \(C\) dont est issue la perpendiculaire. De plus cette macro construit le pied de la perpendiculaire et renvoie les constantes de cette droite, avec le commentaire – qu’il faut adapter comme décrit à la section précédente – Const Hauteur Hc. C’est avec cette macro que l’on trace les trois hauteurs. De plus ayant les constantes des hauteurs, avec deux d’entre elles, on construit l’orthocentre. En pratique, on applique la macro sur les trois coordonnées des sommets du triangle par permutation circulaire sur les trois points, C’est immédiat, il faut juste penser à déplacer l’expression produite entre chaque application.

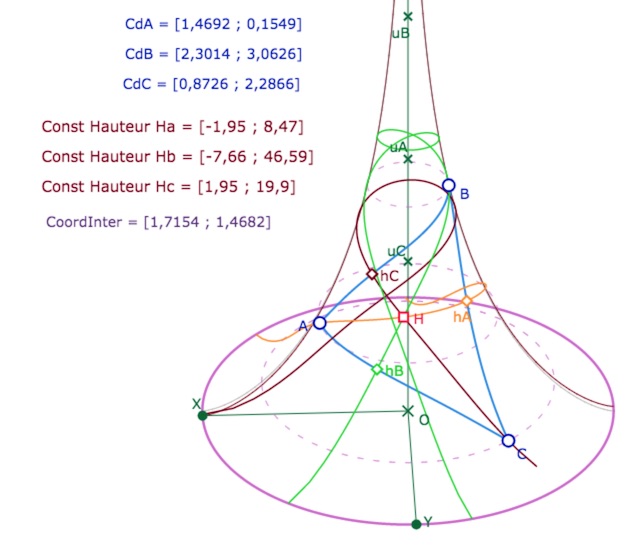
Dans cette illustration, la hauteur issue de \(B\) s’enroule sur plusieurs tours,
on a réglé sa densité à 500 au lieu de 200. Les segments, réglés à 100 peuvent être ramenés à 50.

La question de la perpendiculaire commune

On sait que la pseudosphère ne recouvre qu’une petite partie du plan hyperbolique, environ un quart. Avec les hauteurs, sans visualisation de la situation sur KB, le plus difficile est peut-être de trouver une configuration où la perpendiculaire commune à trois hauteurs est sur la pseudosphère. Car même si l’orthocentre n’est pas sur la pseudosphère, il peut exister dans le plan hyperbolique, et ensuite la perpendiculaire commune prend le relais mais n’est pas, elle non plus, sur la pseudosphère.

Pour les macros, on dispose de deux outils, directement de dessin :
• Dessin 6a : Perp Comm 2 droites qui construit la perpendiculaire commune à deux droite et renvoie ses constantes.
• Dessin 6b : Perp Comm Faisceau 3 droites qui construit la perpendiculaire commune à 3 droites, les intersections avec les droites, renvoie aussi les coordonnées de ces intersection et les constantes de la perpendiculaire commune. C’est cette macro que nous allons utiliser.

Dans a première illustration, on propose au lecteur une situation proche d’une solution. On utilise la macro Dessin 6b un peu à l’aveugle puisque l’on n’a pas la projection dans KB pour évaluer plus finement la configuration dans le plan hyperbolique complet. On voit que ni les coordonnées des points, ni bien entendu les constantes de la perpendiculaire commune ne peuvent être calculées Et donc que rien n’est construit.

Remarque pratique : pour l’illustration suivante, on a remis la hauteur issue de \(B\) à une densité de 200 et réglé celle issue de \(C\) à une densité de 500. Les pieds des hauteurs issues de \(B\) et de \(C\) sont bien entendu sur les droites support des côtés – non tracées pour plus de visibilité – mais pas sur les segments.

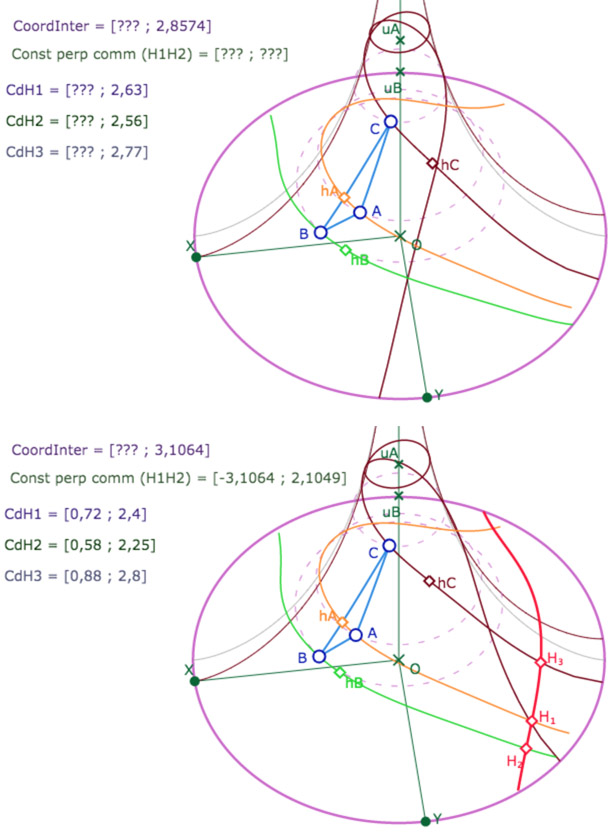
Dans la seconde illustration, on a déplacé le point \(A\) de quelques pixels seulement, et tout est calculé et tracé.

Médiatrices et cercle circonscrit

Éventuellement, ouvrir une nouvelle fois la figure de base (pour conserver la figure précédente par exemple).

Dans la page traitant de l’orthogonalité sur la pseudosphère, on a mentionné que les formules générales sur la perpendiculaire à une droite issue d’un point ne s’appliquent pas si le point est sur la droite. Il y a donc un traitement spécial pour ce cas, et en particulier pour les médiatrices avec, donc, des macros spécifiques.

• Expression 4 : ConstMed et CdMilieu qui, étant donnés deux points renvoie les constantes de la médiatrice et les coordonnées du milieu.
• Dessin 5 : Médiatrice et coord qui fait la même chose mais en traçant la médiatrice. C’est celle que nous allons utiliser. Il faut tout de même tracer le milieu depuis ses coordonnées (Dessin 3) – si on veut le tracer.

On arrive rapidement à cela

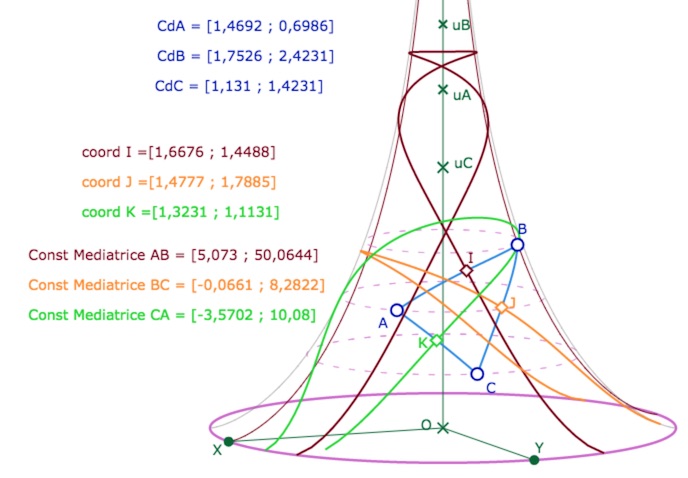
L’intérêt principal de cette activité est dans la construction de nos premiers cycles sur la pseudosphère. Tout d’abord le cercle circonscrit. On commence par construire le centre du cercle circonscrit comme intersection de deux médiatrices. Puis on applique
• Dessin 7 : Cercle par centre et point

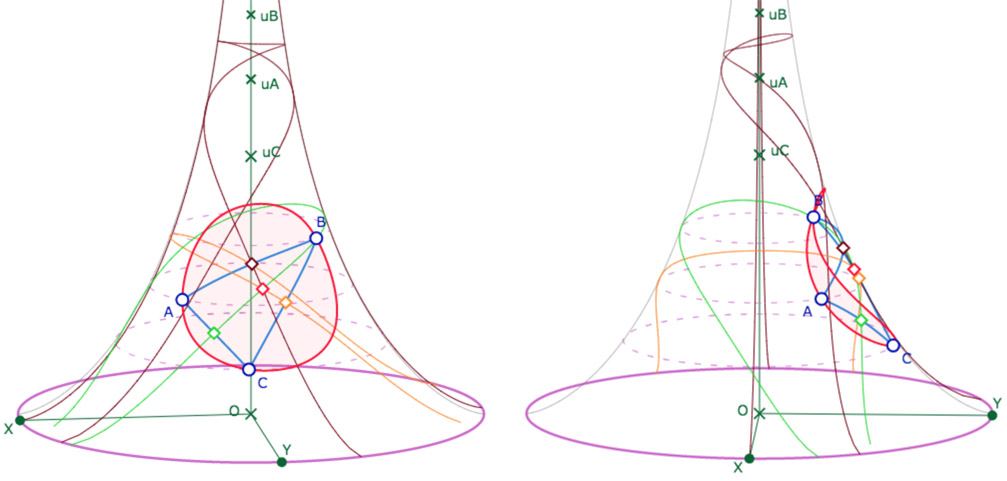
Vue de face et de profil. Le point rouge est bien-sûr le centre du cercle.
On rempli le cercle avec « opacité » (à 0,06) de l’inspecteur d’objets sur le cercle.

Utilisation de la macro Distance (Expression 7)

On a nommé le centre du cercle \(Occ\) le centre du cercle circonscrit. C’est l’occasion de « tester » la macro distance, ci-dessous juste entre le centre du cercle et les sommets. On pourrait aussi l’appliquer sur les milieux.

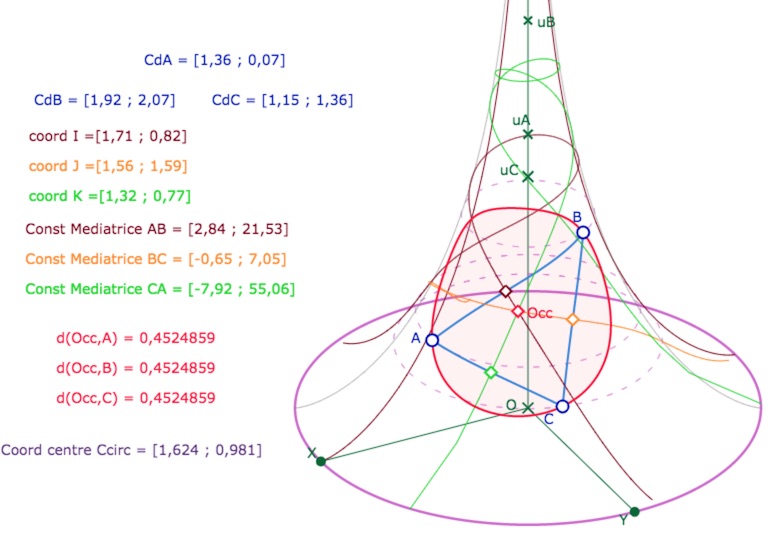
On peut ensuite agrandir le cercle, en déplaçant les points de base et leurs latitudes. Voici un cercle sur presque une feuille entière et sa vue de dessus

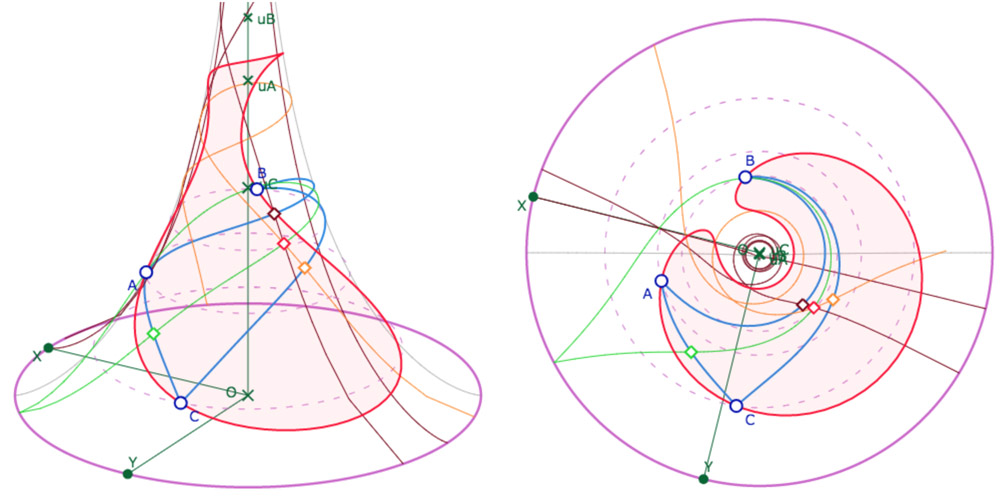
Et on peut aller un peu plus loin avec un cercle sur plusieurs feuilles et une médiatrice « très enroulée » .
Vue de face et de profil de la même configuration.

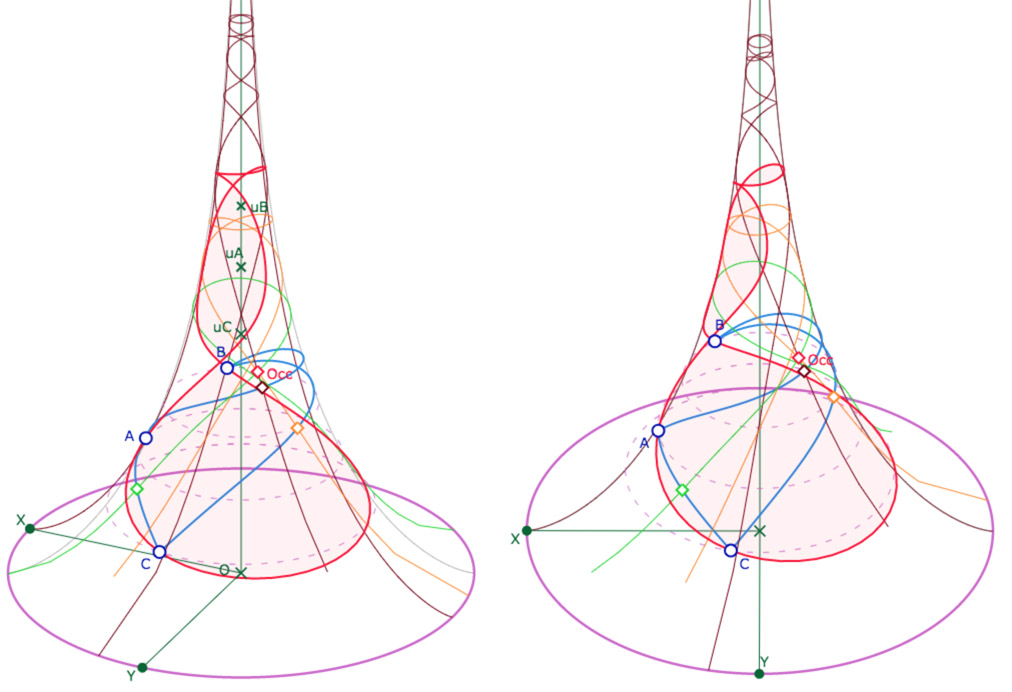
On peut obtenir un cercle circonscrit multifeuille avec des médiatrices se déployant sur juste un peu plus d’une feuille.

Dans la macro Cercle, on ne traite pas le cas où le cercle sort de la pseudosphère. On évitera donc ces configurations … il y a de quoi explorer sans cela.

Médiatrices et équidistante

Cette section est l’occasion d’entrer un peu plus en détail dans le fonctionnement du logiciel, dans le paragraphe « conseil technique préalable ».

On propose de poursuivre la figure pour ajouter l’équidistante quand les médiatrices sont en faisceau à axe. Avant cela, il faut d’abord se placer dans une configuration où les médiatrices ont une perpendiculaire commune … et qu’elle soit sur la pseudosphère.

Construire la perpendiculaire commune aux médiatrices

On a déjà vu, avec les hauteurs, la macro très complète que l’on va utiliser, Dessin 6b. Pour fluidifier la manipulation de la figure, on peut – éventuellement – supprimer le cercle circonscrit. Pour cela il suffit de supprimer les coordonnées du centre du cercle circonscrit.

• On rappelle que l’on applique toujours un peu à l’aveugle la macro Dessin 6b sans savoir si les trois pieds des perpendiculaires \(H_1, H_2, H_3\) sont bien sur la pseudosphère.

Un conseil technique préalable à l’utilisation de Dessin 6b sur cette figure :
On a vu que les expressions produites par les macros ont une position statique. Une conséquence est que si on a tourné la pseudosphère dans tous les sens dans les constructions précédente – comme c’est le cas de l’auteur de l’article – on peut ne pas voir à l’écran les constantes de la perpendiculaire commune, indispensable pour construire l’équidistante … et ne pas pouvoir les récupérer – sauf à modifier le fichier manuellement, ce qui n’est pas envisagé ici. Pour éviter cela trois options sont possibles :
• la plus simple est de replacer la figure déjà construite dans une position proche de la position initiale, par rapport au repère du logiciel s’entend. Pour cela, afficher les axes du repère en activant la dernière icone du tableau de bord (sous forme d’axes), et déplacer à l’écran la souris enfoncée, vers la gauche ou vers la droite – le repère défile alors – pour que les repères soient plus ou moins comme cela :

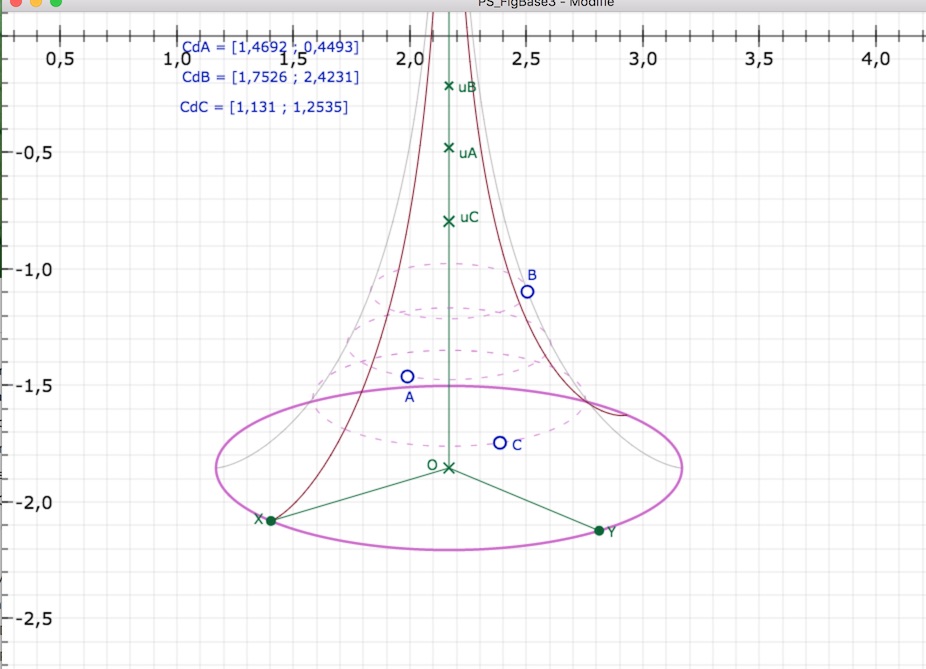
L’objectif est d’avoir à l’écran les abscisses entre 1 et 3, et les ordonnées entre 0 et -2,
car c’est dans cette partie que sont affichés les retours des macros. Désactiver ensuite l’icone des axes.

Cette option, a priori, ne prend que quelques secondes.
• L’autre option, plus radicale, est de relancer la figure initiale et de refaire rapidement la construction des médiatrices, sans par exemple reconstruire les milieux qui ne servent pas pour la suite.
• Une option intermédiaire entre les deux est de lancer la macro Dessin 6b et de voir si au moins deux des coordonnées des trois points \(H_1, H_2, H_3\) sont à l’écran. Dans ce cas, on peut retrouver les constantes de la perpendiculaire commune simplement en appliquant Expression 1 (Constantes d’une droite) à ces deux coordonnées. Et sinon, faire un retour arrière (icone de droite du tableau de bord) pour supprimer l’application de cette dernière macro.

On arrive donc à la construction de la perpendiculaire commune – ci-dessous un exemple de configuration où elle est bien sur la pseudosphère – avec, d’une façon ou d’une autre, les constantes de la perpendiculaire commune à l’écran.

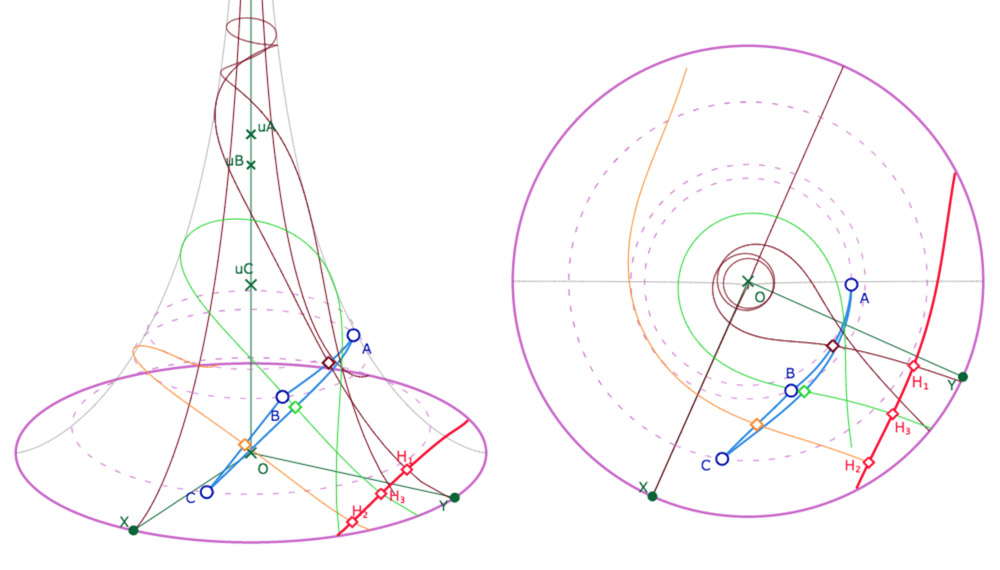
Exemple de configuration d’un triangle où la perpendiculaire commune des médiatrices est sur la pseudosphère.

L’équidistante passant par les trois sommet du triangle

Il suffit d’utiliser la macro Dessin 8 : Equidistante CstAB CdM appliquée
• aux constantes de la perpendiculaire commune aux médiatrices et
• aux coordonnées de l’un des trois sommets, par exemple \(B\).

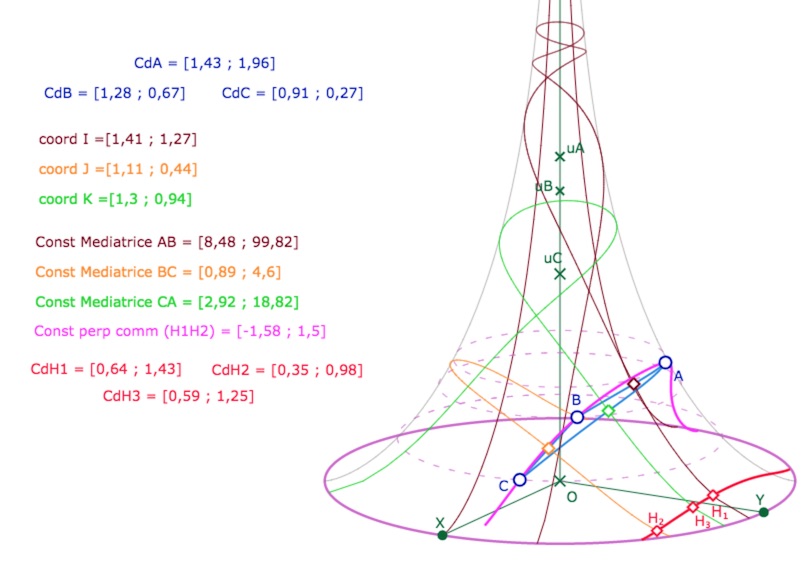
L’équidistante (rose) définie par la perpendiculaire commune (rouge) et un sommet passe bien par les deux autres sommets.

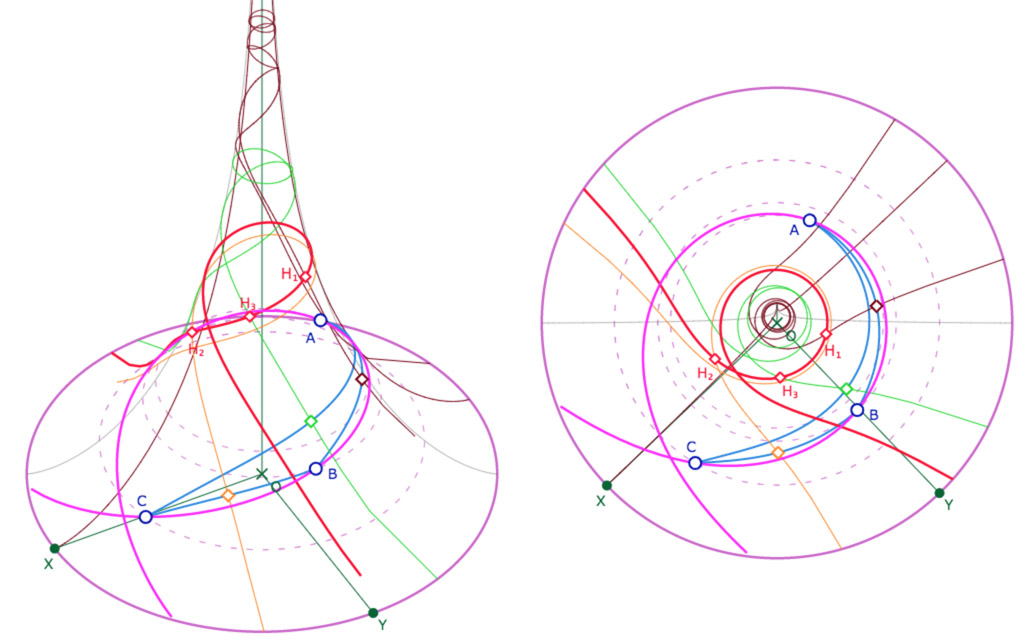
Exemple ou la perpendiculaire commune aux médiatrices est sur plus d’une feuille,
et de même pour l’équidistante (vue de face et de dessus de la même configuration)

Illustration de la propriété de l’équidistante

La figure précédente n’est pas nécessairement facilement maniable. En fait les densités des dernières constructions peuvent être élevées, on peut les remttre à 200/
On propose dans cette section :
• de réaliser une équidistante d’application immédiate pour voir la forme qu’elle peut prendre sur la surface. On rappelle que l’équiditsante à une droite n’est une droite qu’en géométrie euclidienne.
• d’illustrer sa propriété de distance constante à la droite.

Équidistante de base

• Relancer la figure de base
• Appliquer Expression 1 (constantes d’une droite) aux points \(A\) et \(B\). Il n’est pas nécessaire de renommer le commentaire.
Puis appliquer Dessin 8 : Equidistante CstAB CdM aux constantes de la droite \((AB)\) et aux coordonnées du point \(C\).

On obtient une figure un peu ordinaire dans la configuration initiale que l’on peut modifier en agissant sur les trois points ou leurs latitudes pour obtenir des équidistantes plus originales comme ci-dessous. Dans cette illustration, on a augmenté la latitude de \(C\) et, significativement, sa longitude.

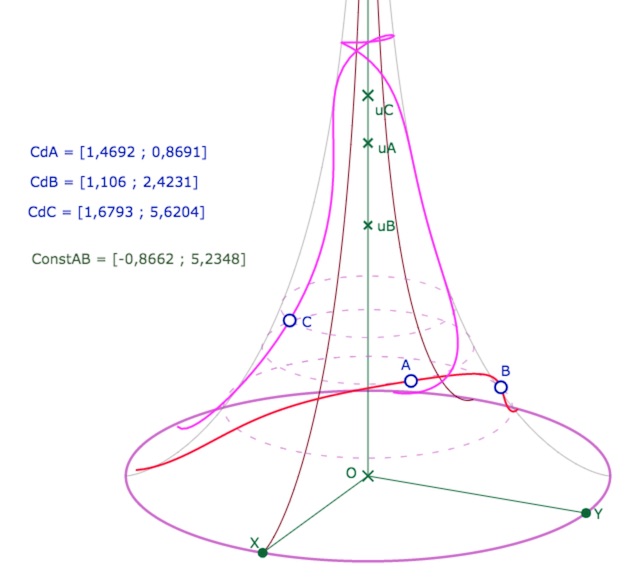
L’intérêt d’une telle figure serait de vérifier que l’on a vraiment construit une « équidistante » : le lieu des points à même distance de la droite \((AB)\) que le point \(C\). Mais cela n’est pas si simple depuis cette figure car si on prend un point \(M\) sur objet de la droite \((AB)\) ou sur l’équidistante, on n’a aucun moyen de récupérer ses coordonnées beltramiennes \([u_M, \theta_M]\). Il faut procéder autrement.

Illustration que l’équidistante est bien « à distance constante » de la droite.

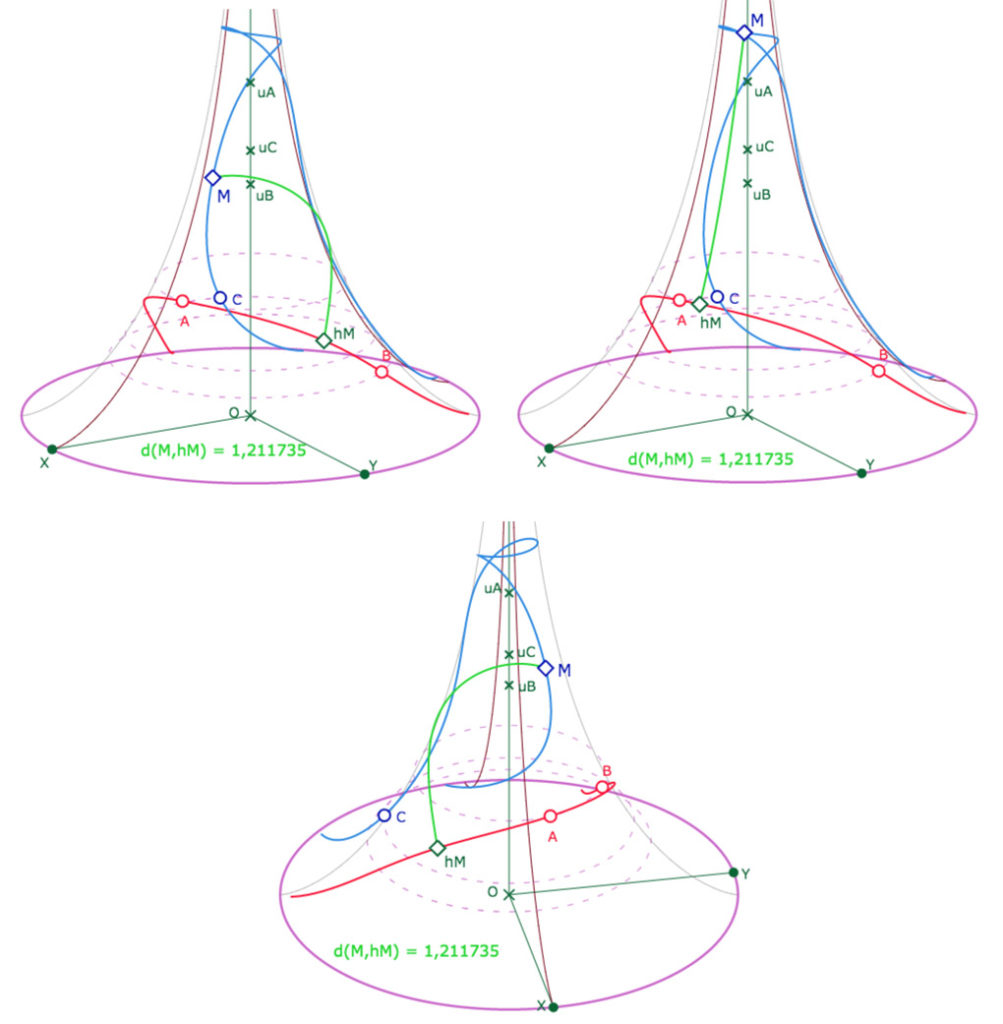
Une figure à finaliser est proposée aux lecteurs. On va pouvoir manipuler un point \(M\) sur l’équidistante (désormais en bleu clair), le projeter sur la droite \((AB)\) – désormais en rouge – en un point \(h_M\) et calculer \(d(M,h_M)\) pour illustrer que c’est une constante.

Pour cela on se donne un point d’un segment qui va représenter une longitude. A partir de cette longitude on a construit un point \(M\) sur l’équidistante depuis ses coordonnées calculées \(CdM\). Cet aspect sera détaillé à la figure suivante.

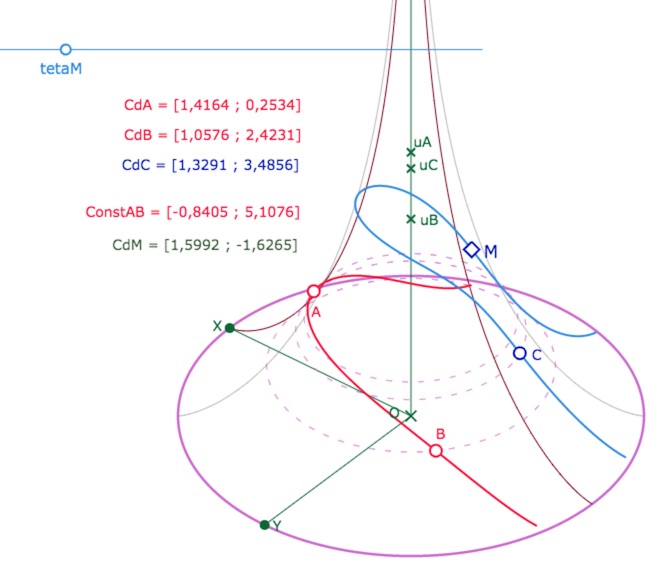
Dans cette figure, on déplace \(\theta_M\) sur le segment, \(M\) se déplace sur l’équidistante. Il faut tourner la pseudosphère pour accéder à toute l’amplitude de \(\theta_M\). Comme on l’a détaillé dans la section précédente, il est conseillé de le faire après la construction proposée.

Lancer cette figure spécifique dans un nouvel onglet.

Construction proposée

• Construire de projeté orthogonal \(h_M\) du point \(M\) sur la droite \((AB)\). Pour cela utiliser la macro Expressions 5a : Coord Pied Hauteur CstAB C puis Dessin 3 pour construire \(h_M\).
• Disposant des coordonnées de \(M\) et \(h_M\), on peut construire le segment, calculer la distance entre ces deux points et vérifier que cette distance est constante quand \(M\) se déplace sur l’équidistante.

Horicycle par symétrie orthogonale

En géométrie hyperbolique, l’horicycle de centre idéal \(O\) (un point à l’infini) passant par \(A\) est le lieu des symétriques de \(A\) par le faisceau des droites ayant \(O\) comme point à l’infini. Sur la pseudosphère, on a déjà vu que les cercles parallèles à l’équateur (comme les trois cercles en pointillé ci-dessus) sont des parties d’horicycles. Plus précisément l’horicycle associé à un cercle parallèle à l’équateur est l’enroulement infini – dans les deux sens – sur ce cercle.

Tous ces horicycles sont concentriques en le seul point idéal accessible à la pseudosphère. Pour construire d’autres (parties) d’horicycles sur la surface, il suffit de faire le symétrique d’un de ces cercles par rapport à une droite, on même un point, et donc cela peut se faire directement sur la pseudosphère avec les outils dont on dispose.

Dans cette section, on propose au lecteur de réaliser une telle construction depuis une figure adaptée à cela, en particulier avec une macro supplémentaire pour éviter quelques difficultés.

La construction proposée est très simple et se fait en une minute (deux si on veut « décorer » la construction). Le plus long est clairement de lire les justificatifs et commentaires de la procédure.

Présentation de la situation

On dispose d’un cercle (orange) support, de latitude \(u_M\). On se propose de faire le symétrique de ce cercle par rapport à la droite \((AB)\). On dispose d’un point \(M\) sur le cercle, il suffit de faire le symétrique de \(M\) et le lieu de ce symétrique. Mais cela ne fonctionne pas – avec ce logiciel – parce que ce cercle est un « cercle 3D » et le lieu lié à un point à un tel cercle n’a pas été implémenté dans DGPad. Il faut donc faire autrement.

On reprend donc une technique proche de celle pour l’équidistante, sauf qu’ici, le lecteur intéressé est invité à construire le lieu lui-même. On aurait pu le faire dans l’équidistante, c’est la même technique, mais on a voulu graduer, non pas les difficultés – il n’y en a pas – mais plutôt les engagements cognitifs associés.

Pour parcourir un point sur le cercle euclidien de latitude \(u_M\), on a fait parcourir à un point \(Pt_{FP}\) un segment de longueur \(\pi\) (pour que cela rentre à l’écran) et la longitude du point sur la feuille principale est donc \(2(x_{PtFP}-x(o_{FP})\), sa latitude est la côte du point \(u_M\) soit \(uM[2]\) dans la notation du logiciel. On a ainsi construit « manuellement » les coordonnées beltramiennes du point \(P_{hori}\).

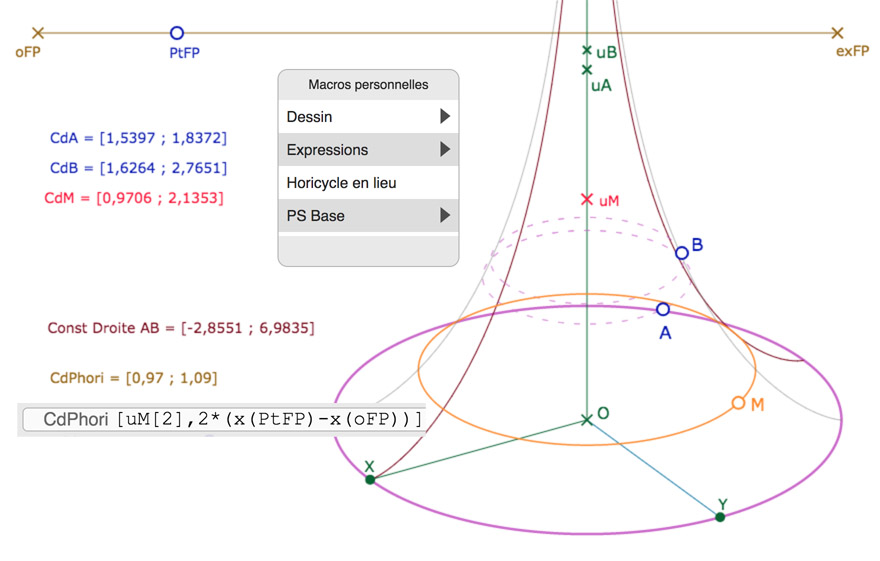
Tout le reste de la construction se fait par des macros. Vous aurez noté que l’on a ajouté une macro Horicycle par lieu, au premier niveau, pour finaliser la construction. C’est juste une application de lieu de point et donc, exceptionnellement, pour appliquer cette macro il faudra montrer des points à l’écran et non pas des coordonnées.

Réalisation de la figure

Commencer par ouvrir cette figure dans un nouvel onglet. Elle contient, comme le montre le montage ci-dessus, la même structure de macro-constructions. Nous allons faire une construction « minimaliste » pour montrer que peu d’objets sont nécessaires et en particulier nous n’allons pas tracer la droite \((AB)\). On garde ça pour « la minute décoration ». Il y a 5 macros à appliquer.
• Placer le point \(P_{hori}\) sur la pseudosphère en appliquant Dessin 3 (Point par Coord) à ses coordonnées \(CdP_{hori}\). Il n’est pas nécessaire de le nommer.
• Construire les coordonnées du projeté orthogonal de \(P_{hori}\) sur la droite \((AB)\) en appliquant Expressions 5a (Coord Pied Hauteur CstAB C) à Constante Droite AB et CdPhori. On obtient une expression dont le commentaire est Coord Hc.
• Construire le symétrique de \(P_{hori}\) par rapport à son projeté orthogonal sur \((AB)\) en appliquant Expressions 6b (Coord Sym Ctr Pt) à Coord Hc et CdPhori. On obtient une expression dont le commentaire est Coord Sym Ctr Pt.
• Appliquer Dessin 3 à cette dernière expression : on obtient un nouveau point sur la surface. Ce point est le symétrique orthogonal de \(P_{hori}\) par rapport la droite \((AB)\), et donc un point de l’horicycle que l’on veut construire.
• Enfin, appliquer la nouvelle macro du premier niveau, Horicycle par lieu, en montrant d’abord ce dernier point créé et ensuite le point \(Pt_{FP}\) du segment des longitudes. Le lieu est tracé.

On devrait avoir obtenu cela :

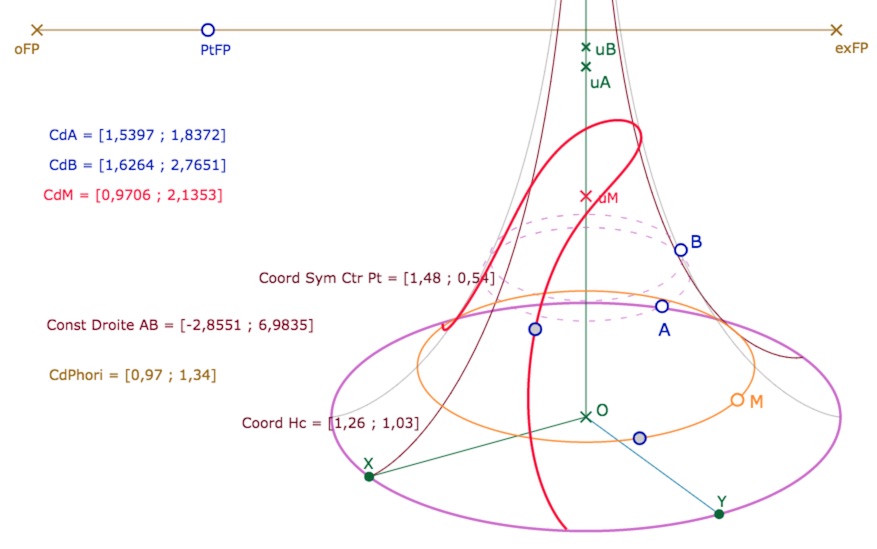
Pourquoi cette macro Horicycle par lieu ?

Il y a bien un outil lieu automatique dans la palette contextuelle des points, mais elle est plutôt pour une utilisation en 2D. L’algorithme prend en général le premier point significatif dont dépend le point final, et il est très efficace en 2D. Mais ici c’est plus complexe à choisir. En effet l’algorithme, a priori élimine les points \(A\) et \(B\) qui ne sont pas traités, mais hésite – ne choisit pas – entre les latitudes \(u_A, u_B, u_M\). D’où cette macro utile pour ce genre de situations.

Amélioration de la figure (la minute de plus)

On peut cacher (icone gomme et non pas corbeille)
• les deux points crées sur la pseudosphère,
• les trois expressions créées (conserver Const Droite AB), et
• tout ce qui concerne la variation de la longitude : le segment, ses extrémités et le point mobile sur le segment.

Puis, on peut reprendre la construction à partir du point \(M\). Pour cela on applique
• Expressions 5a à Const Droite AB et CdM. Cela produit une nouvelle expression Coord Hc.
• Expressions 6b à Coord Hc et CdM qui donne une nouvelle expression encore commentée Coord Sym Ctr Pt
• Dessin 3 aux deux dernière expressions pour placer les points sur la surface
• Dessin 2 (Segment) à CdM et l’expression Coord Sym Ctr Pt.
• Dessin 1 (le tracé de la droite) à Const Droite AB

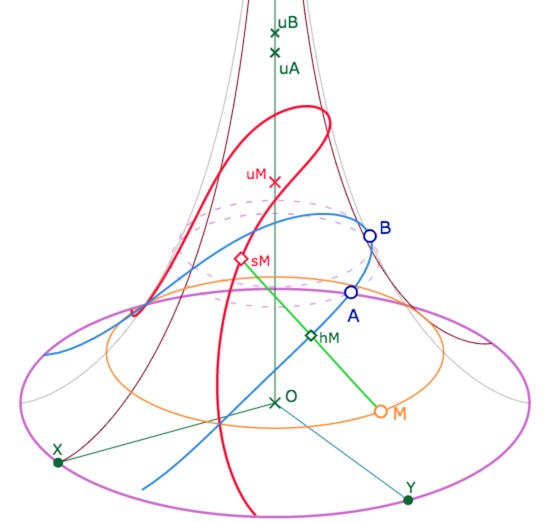
Sympathique, d’autant que l’on peut jouer sur les points \(A\) et \(B\) et leurs latitudes \(u_A, u_B\),
et obtenir des configurations un peu inattendues

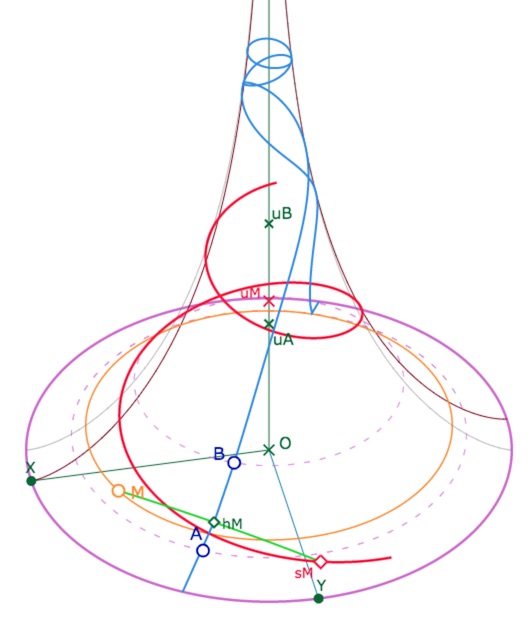
Avec une droite \((AB)\) proche d’un méridien, l’horicycle semble s’enrouler.
A-t-on une situation du type « rêve de Coxeter » ? Qu’en est-il ?

Complément (à faire éventuellement, se placer alors en mode « Calculatrice »)

Comme on a tracé une partie de l’horicycle sur la feuille principale, on peut tenter d’étendre un peu plus en modifiant l’extrémité du segment des longitudes (le point \(ex_{DP}\)). Ce qui donne :

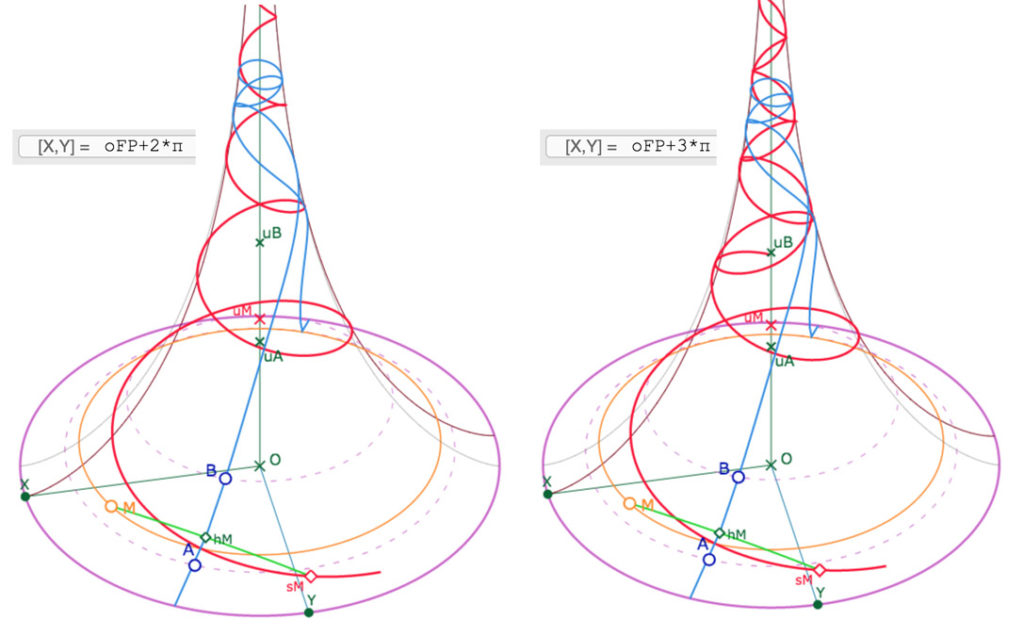
• à gauche : on trace l’horicycle sur deux feuilles : les latitudes de l’horicycle continuent de monter.
• à droite : on le trace sur trois feuilles : les latitudes redescendent.

Comme il n’y a qu’un seul point à l’infini, pour enrouler l’horicycle il faut que la droite \((AB)\) soit proche d’un méridien, sans être un méridien sinon l’horicycle est son propre symétrique. Comme le centre de l’horicycle est l’image par la symétrique d’axe \((AB)\) de \(I_{dl}\), soit un point qui n’est pas dans l’horicycle rose, image de la pseudosphère. Donc nécessairement, l’horicycle image ne peut pas s’enrouler à l’infini et doit nécessairement redescendre. Parce que c’est trop joli, une autre figure, à manipuler dans la page, est proposée sur ce thème en fin d’article.

Présentation des macros non utilisées

Les seules macros non encore utilisées sont

• Expressions 6a : Coord Sym CstPP Ctr Pt qui construit le symétrique d’un point (Pt) par rapport à un autre point (Ctr) – comme 6b déjà utilisée – mais en utilisant les constantes de la droite de ces deux points, si elle est connue, ce qui évite de la reconstruire. C’est une optimisation de 6b.

Et les deux macros du troisième dossier PS Base

Il s’agit de créer un point sur la surface et de calculer ses coordonnées. Pour cela on commence par construire un « cercle-horicycle ».

• PS Base 2 : Horicycle Latitude : Avec un point pris sur le segment vertical, la macro construit le cercle « horicycle ». Son centre est caché, il faut le montrer avec la gomme car il est indispensable pour calculer les coordonnées beltramiennes d’un point du cercle. Il s’appelle \(oH\) (comme préfixe, \(oH, oH_0, oH_1\)).

Une fois ce cercle construit, on place un point dessus avec l’interface usuelle du logiciel, par la palette contextuelle des points. On peut alors obtenir les coordonnées de ce point par :

• PSBase 1 : Coord par A oA uA : cette macro donne les coordonnées d’un point en montrant dans l’ordre, le point, le centre du cercle, la latitude du cercle.

Figure avec les trois points multifeuilles

On peut reprendre les premières constructions simples de cette page sur une figure où les trois points de base peuvent être sur la feuille principale mais aussi sur les deux feuilles adjacentes.

En pratique on utilise les mêmes macros, de la même façon. Seules les longitudes des trois points sont modifiées en fonction de la feuille à laquelle ils appartiennent.

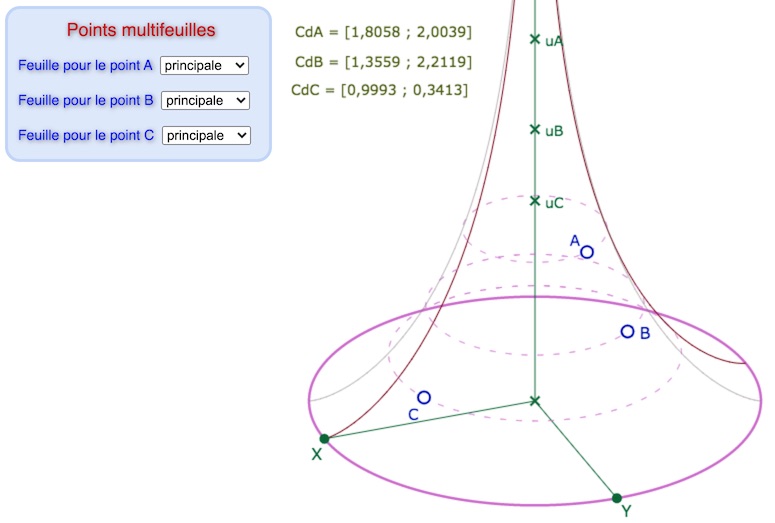
Ouvrir cette figure multifeuilles dans un nouvel onglet.

Il est conseillé de commencer par une figure simple comme les médianes d’un triangle : déjà les segments s’allongent, pour les droites on sera prudent.

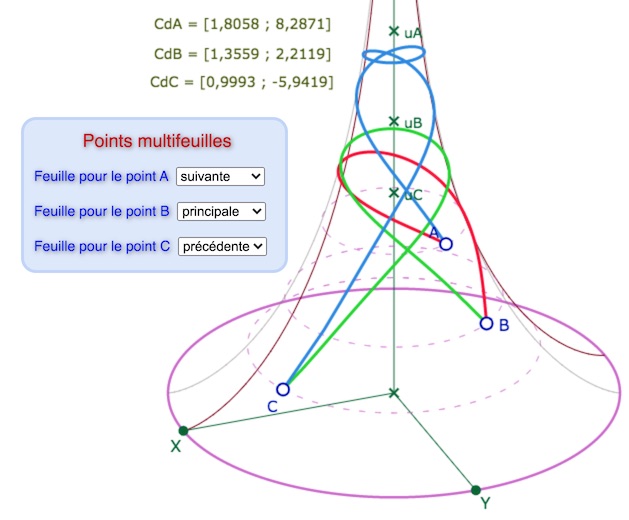
Le segment \([AC]\) est sur trois feuilles
ci dessous, médianes, sur deux feuilles seulement

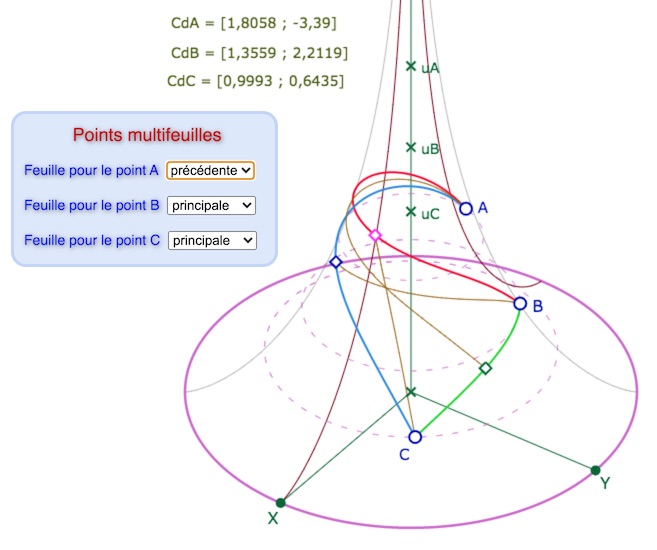
Remarque : il peut être nécessaire d’augmenter la densité non seulement des droites, mais même parfois des segments.

Retour sur l’enroulement de l’horicycle

Dans la figure suivante on a un peu systématisé la construction précédente avec un curseur (on enroule sur \(k\) tours (jusqu’à 12 tours) … hum ce curseur \(k\) n’a aucun rapport avec la constante nommée \(k^2\) des droites. On ne peut plus tracer la droite \((AB)\), trop proche d’un méridien, on a donc préparé une macro un peu spécifique pour tracer un « morceau de droite ».

Dans la figure suivante, on peut modifier le curseur \(k\) bien entendu, mais aussi les points \(A\) et \(B\) juste de quelques pixels, dans un sens ou l’autre, ajuster éventuellement leurs latitudes \(u_A\) et \(u_B\). On regardera aussi la seconde constante – dite \(k^2\) – de la droite \((AB)\). Voici ce que l’on peut obtenir :

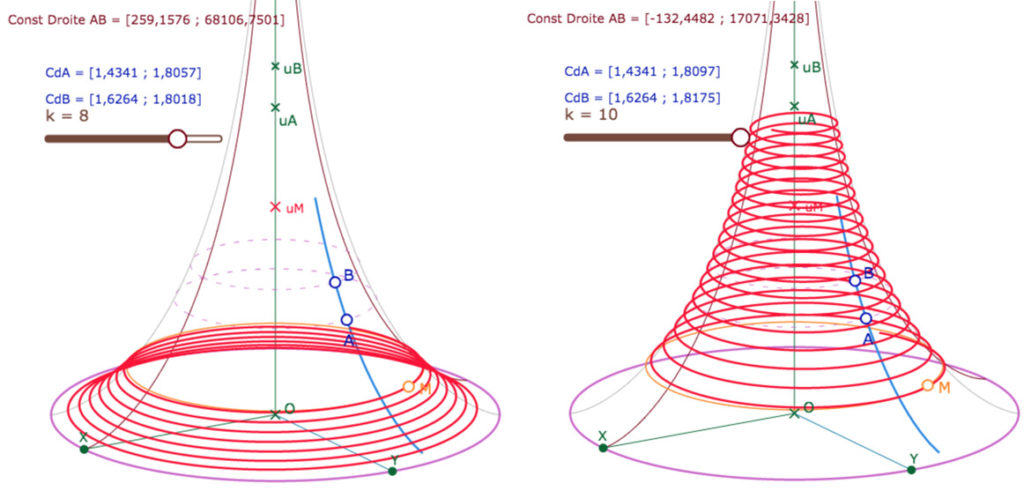
à gauche, enroulement vers l’équateur (\(k^2>68000\)), à droite, enroulement vers l’infini.

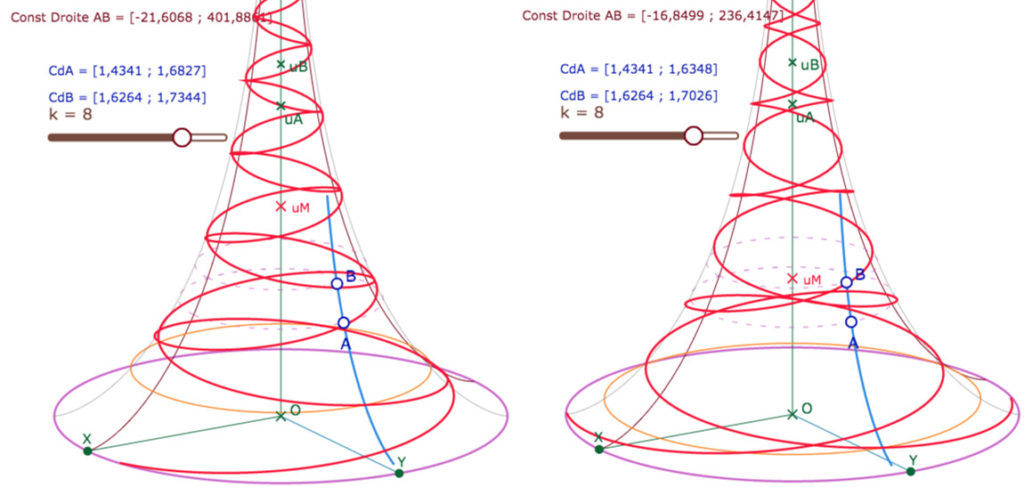
Deux exemples de départ de l’équateur avec retour à l’équateur. A droite on a diminué la latitude \(u_M\).

La figure manipulable

Préférer ouvrir cette figure hors iframe dans un nouvel onglet