Cet article est centré sur des calculs trigonométriques pour aboutir à la démonstration du théorème de Engel, celui-ci servant ensuite, dans un autre article, à la construction géométriques de triangles d’angles donnés.
Rappels sur la trigonométrie hyperbolique
Ces formules ont été présentées dans ce premier article sur le manuscrit de Bolyaï. On trouve une démonstration de ces résultats, avec nos outils et notations contemporaines, dans tout ouvrage consacré aux géométries non euclidiennes.
Ainsi, cet article reprend, pour la démonstration du théorème de Engel, la preuve de Martin Jay Greenberg dans son Euclidean and Non Euclidean Geometries (3° éditions p.411 et suivantes)
Autour de l’angle de parallélisme
On se souvient que Bolyaï avait des notations très personnelles que même son traducteur, Jules Houël, commentait comme ici :
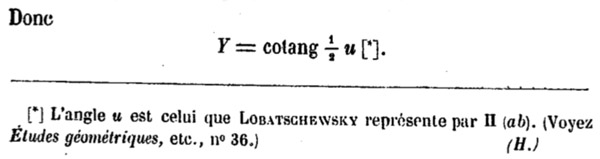
La formule montrée par Bolyaï s’écrit maintenant \(\displaystyle tan \left( \frac{\Pi(x)}{2} \right) = e^{-x}\).
Autres expressions équivalentes
\(\displaystyle sin \, \Pi(x)=\frac{1}{ch \, x} \quad tan \, \Pi(x)=\frac{1}{sh \, x} \quad cos \, \Pi(x)=th \, x\).
La fonction réciproque de \(\Pi\), notée \(\Delta\) depuis Lobatchevsky, qui donne la longueur d’un segment correspondant à l’angle de parallélisme \(\alpha\), vérifie \(\Delta(\alpha) = ch^{-1} \displaystyle \left( \frac{1}{sin \, \alpha} \right)\) (formule due à Lobatchevsky). Dans cet article, elle sera utilisé uniquement pour une vérification numérique dans une illustration u théorème de Engel, même si il y avait aussi un moyen de s’en passer.
Trigonométrie dans un triangle
La formule des sinus : \(\displaystyle \frac{sin \, A}{sh \, a} = \frac{sin \, B}{sh\, b} = \frac{sin \, C}{sh \, c}\).
Relations entre angles et côtés
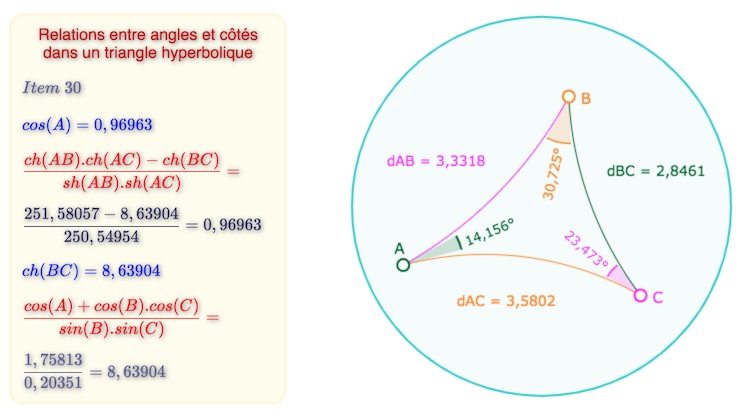
Ouvrir la figure associée à cette illustration, dans un nouvel onglet.
Cas du triangle rectangle
Relations qui dans le cas du triangle rectangle se simplifient et donnent :
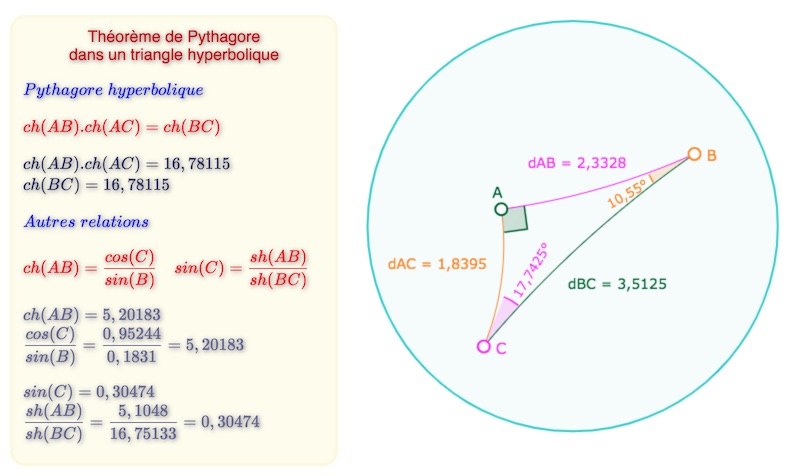
Ouvrir la figure associée à cette illustration, dans un nouvel onglet.
Dans un triangle \(ABC\), rectangle en \(A\), outre les trois relations présentées dans la figure précédente, on a aussi les relations :
\(\displaystyle cos \, \widehat{C} = \frac{th \, AC}{th\, BC} \quad et \quad tan \, \widehat{C} = \frac{th \, AB}{sh \, BC}\).
Ces formules dans le triangle rectangle seront systématiquement utilisées dans la suite de cet article.
Du quadrilatère de Saccheri
à celui de Lambert
Saccheri a trouvé de nombreux résultats hyperboliques, sur la base de l’étude du quadrilatère qui porte son nom. Résultats qu’il a fini par rejeter en fin d’ouvrage, ne pouvant accepter le concept que, si une telle géométrie (dite « de l’angle aigu ») avait du sens, elle devait être non connectable (la géométrie euclidienne vérifiant les axiomes du rectange et de connexion), puisqu’il avait conscience que certaines droites (les futures parallèles) devraient avoir alors leur unique perpendiculaire commune … rejetée à l’infini … « ce qui nuit à la nature de la droite » … selon sa formule restée célèbre.
On se propose ici de faire quelques calculs dans le quadrilatère de Saccheri, pour les appliquer dans celui de Lambert.
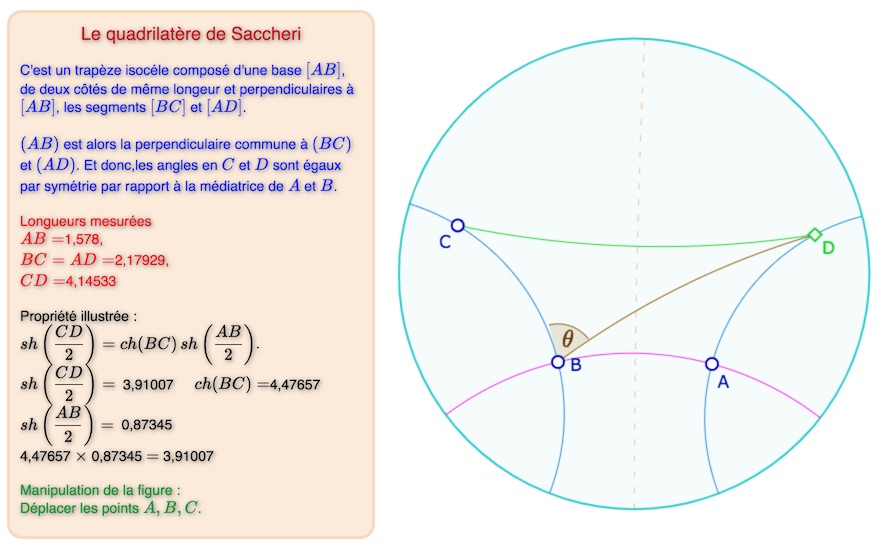
Lancer cette figure dans un nouvel onglet
Preuve du résultat
Notons \(m=AB, p=BC, k=CD\) et \(d=BD\). La formule « des cotés » dans le triangle \(BCD\), on a \(ch \,k = ch \,p \; ch \, d – sh \, p \; sh \, d \; cos \, \theta\).
Par ailleurs \( cos \, \theta = \displaystyle sin ( \frac{\pi}{2} – \theta) = \frac{sh \, k}{sh \, d} \) (formule dans le triangle rectangle \(BAD\)) et (Pythagore) \(ch \, d = ch \, p \; ch \,m\).
Ainsi \(ch \,k = ch^2 p \; ch \,m – sh^2 p = ch^2 p \left( ch \, m -1 \right)\), par \(ch^2-sh^2=1\).
Et en utilisant cette relation des angles moitiés \(\displaystyle 2 sh^2 \frac{x}{2} = ch \, x -1\), on a \(ch\, k = ch^2 p \times \displaystyle 2 sh^2 \left( \frac{m}{2} \right) +1\), soit \(ch \, k -1 = ch^2 p \times \displaystyle 2 sh^2 \left(\frac{m}{2} \right)\) et donc \(\displaystyle 2 sh^2 \left( \frac{k}{2} \right) = ch^2 p \times 2 sh^2 \left( \frac{m}{2} \right)\), soit, puisque tout est positif,
\(\displaystyle sh \left( \frac{k}{2} \right)= ch \, p \; sh \left( \frac{m}{2} \right)\)
De Saccheri à Lambert
Dans la figure précédente la médiatrice de \([AB]\), comme axe de symétrie de \(ABCD\) est aussi perpendiculaire commune à \((AB)\) et \((CD)\) et comme axe de symétrie coupe \([CD]\) en son milieu. Ainsi, en renommant les points – pour la suite – on a la situation suivante.
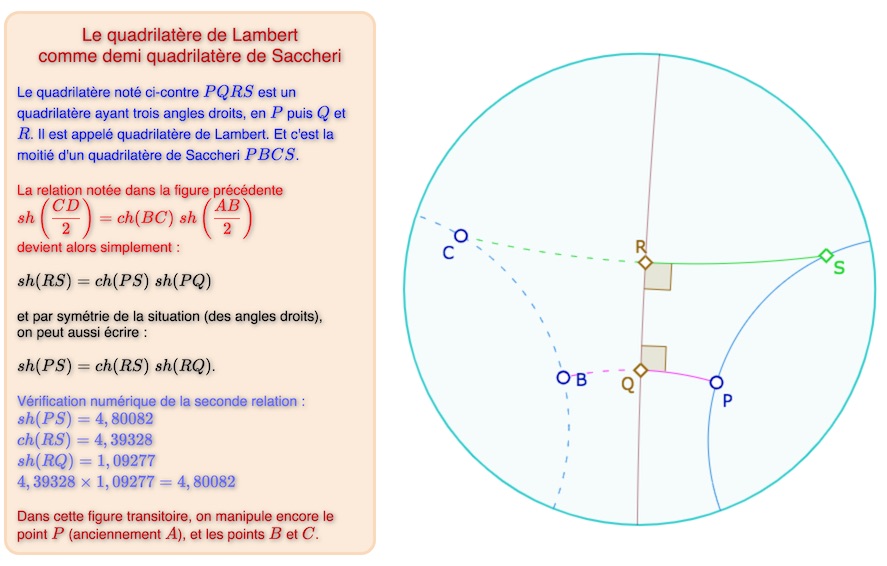
Lancer cette figure dans un nouvel onglet
Calculs dans le quadrilatère de Lambert
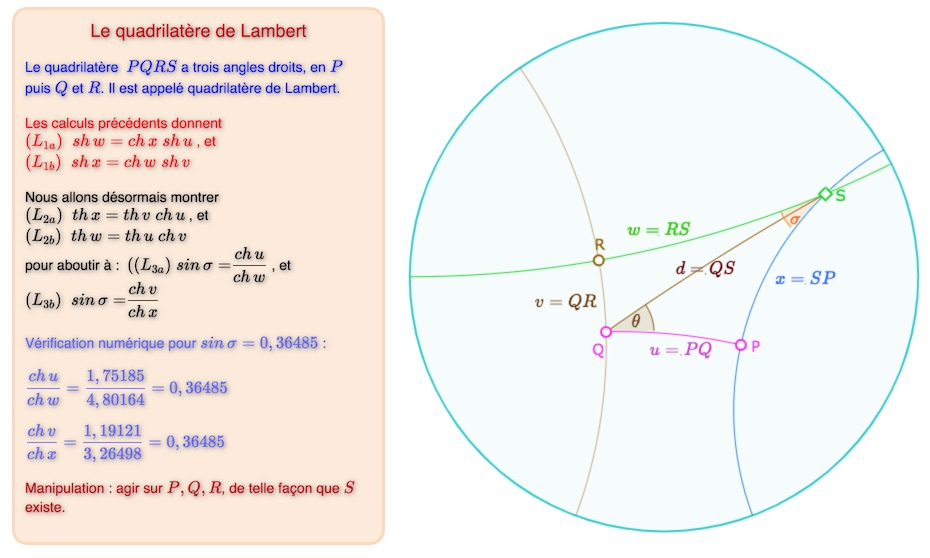
Lancer cette figure dans un nouvel onglet (plus grande, plus lisible)
Preuve de \(L_{2a}, L_{2b}\)
Les formules du triangle rectangle dans le triangle \(QPS\) permettent d’écrire \(sin \, \theta = \displaystyle \frac{sh \,x}{sh \, d}\), soit \(sh \, x = sin \, \theta \; sh \, d = \displaystyle \cos \left( \frac{\pi}{2} – \theta \right) \; sh \, d = \frac{th \, v}{th \, d} sh \, d = th \, v \; ch \, d\).
Pythagore dans le triangle \(QPS\) permet d’écrite \(ch \, d = ch \, u \; ch \, x\), soit, au final \((L_{2a}) \; \; th \, x = th \, v \; ch \, u\). De même, par symétrie structurelle de la figure, on a aussitôt \((L_{2b}) \; \; th \, w = th \, u \; ch \, v\).
Preuve de \(L_{3a}, L_{3b}\)
On se place dans le triangle \(SPR\). On note \(\sigma\) l’angle \(\widehat{RSP}\). On applique la formule des sinus dans \(SPR\) :
\(\displaystyle \frac{sin \, \sigma}{sh \, PR} = \frac{sin \, \widehat{SPR}}{sh \, w} = \frac{cos \, \widehat{QPR}}{sh \, w} = \frac{th \, u}{th \, PR \; sh \, w}\), toujours par la formule du cosinus d’un angle dans un triangle rectangle. Soit après simplification par \(sh \,PR\) il vient simplement \(sin \, \sigma = \displaystyle \frac{th \, u \; ch \, PR}{sh \, w}\). Pythagore dans \(PQR\) permet d’écrire \(ch \, PR = ch \, u \; ch \, v\), et en utilisant \(L_{1a}\) on peut écrite \(sin \, \sigma = \displaystyle \frac{th \, u \; ch \, u \; ch \, v}{sh \, u \; ch \, x}\), soit \((L_{3a}) \; \; sin \, \sigma = \displaystyle \frac{ch \, v}{ch \, x} \).
De même, par symétrie (« côté opposé sur côté adjacent »), et \(L_{1b}\), on a aussi \((L_{3b}) \; \; sin \, \sigma = \displaystyle \frac{ch \, u}{ch \, w} \).
Segments complémentaires
Un cas limite du quadrilatère de Lambert a historiquement longtemps été utilisé pour étudier la construction de triangles d’angles donnés. Ce cas limite est celui où le point \(S\) ci-dessus devient un point idéal, ou encore quand les segments notés \(x\) et \(w\) ci-dessus deviennent des droites parallèles. Dans ce cas les segments \(u\) et \(v\) sont tels que les angles \(\Pi(u)\) et \(\Pi(v)\) sont complémentaires.
Deux segments seront dits complémentaires si leurs angles de parallélisme le sont :
\(x^*\) est dit complémentaire de \(x\) si \(\Pi(x)+\Pi(x^*) = \displaystyle \frac{\pi}{2}\).
On peut alors écrire \(x^* = \Delta \left( \displaystyle \frac{\pi}{2}-\Pi(x) \right) = ch^{-1} \displaystyle \left( \frac{1}{sin \, \Pi(x^*)} \right)\). Et donc \(ch \, x^* = \displaystyle \frac{1}{sin (\displaystyle \frac{\pi}{2}-\Pi(x))} = \frac{1}{cos \, \Pi(x)}= \frac{1}{th \, x}\)
Avec les relations de trigonométrie hyperbolique \(ch^2-sh^2=1\) et \(1 – th^2 = \displaystyle \frac{1}{ch^2}\) on aboutit ensuite rapidement à \(sh x^* = \displaystyle \frac{1}{sh \, x}\). Et donc \(th x^* = \displaystyle \frac{1}{ch \, x}\)

Ouvrir la figure associée à cette illustration dans un nouvel onglet.
La figure ci-dessus est spécifique au modèle du disque de Poincaré car nous avons explicitement utilisé un point idéal pour construire le point \(C\). Mais une construction purement hyperbolique du segment complémentaire est possible car c’est le cas de l’angle de parallélisme comme détaillée dans ce même article sur Bolyaï.
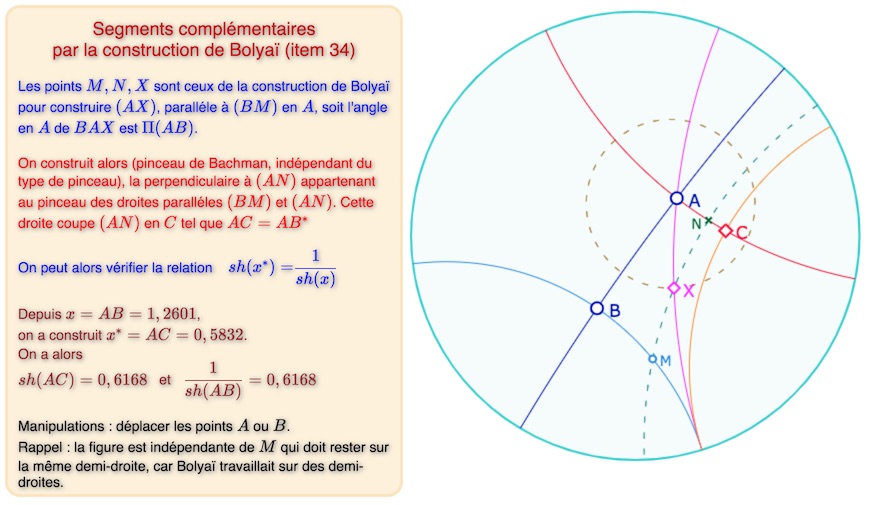
On a utilisé la notion de pinceau qui n’était bien entendu pas encore d’actualité – juste car on dispose de macros désormais usuelles – mais à l’époque de Engel, on savait construire la perpendiculaire à une droite issue d’une famille de droites parallèles, puisque c’est aussi une des définitions des horicycles.
Lancer cette figure dans un nouvel onglet
Le théorème de Engel
On se donne deux angles \(\alpha \) et \(\beta\), avec \(\displaystyle \alpha + \beta < \frac{\pi}{2}\). Si, certes, il existe toujours un triangle rectangle dont les angles aigus soient \(\alpha \) et \(\beta\), l’existence d’un tel triangle reste assujetti à des conditions de longueurs. Historiquement, on a commencé à étudier la correspondance entre les triangles rectangles et les quadrilatères de Lambert.
Un des premiers résultats associe l’existence d’un triangle rectangle ayant deux angles donnés à celle d’un quadrilatère de Lambert, de la façon suivante ;
Théorème de Engel (1867) : Il existe un triangle \(ABC\), rectangle en \(C\), d’angle en \(A, \; \alpha\) et d’angle en \(B, \; \beta\) si et seulement si il existe un quadrilatère de Lambert \(PQRS\), rectangle en \(P, Q, R\) tel que \(PQ=AC, \; RS=AB\) avec \(\alpha=\Pi(QR^*)\) et \(\beta=\Pi(SP)\), où \(QR^*\) est le complémentaire de \(QR\). Dans ce cas on a de plus \(\sigma = \Pi(BC)\)
Deux figures d’illustration sont proposées après la preuve
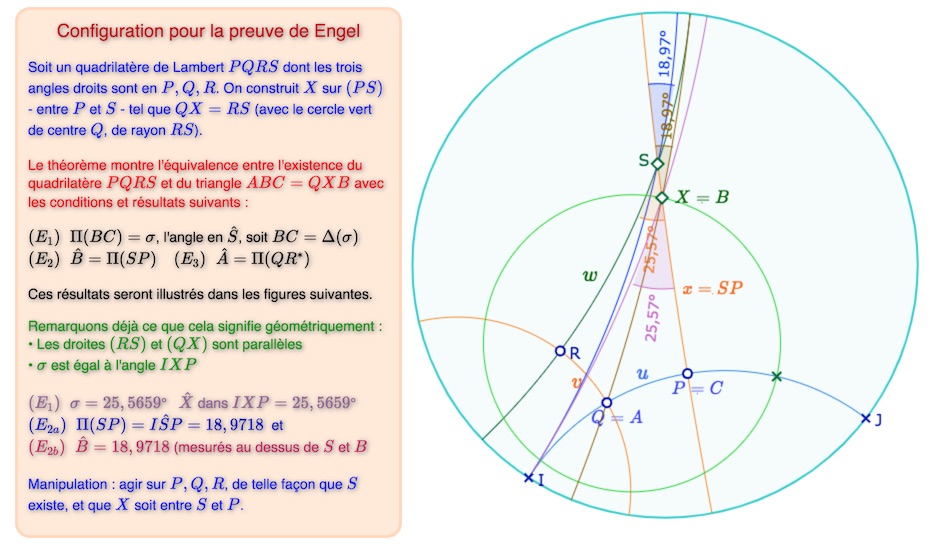
Simplicité et (grande) subtilité de la configuration étudiée par Engel, en particulier
le parallélisme des droites \((QX)\) et \((RS)\)
Lancer cette figure dans un nouvel onglet (plus lisible)
Preuve du théorème : les calculs
\(X\) est donc le point du segment \([PS]\) tel que \(QX=RS=w\). Le triangle \(ABC\), rectangle en \(C\) est le triangle \(QPX\), rectangle en \(P\).
• La formule du sinus d’un angle dans un triangle rectangle permet d’écrire \(sin \; \hat{B} = \displaystyle \frac {sh(PQ)}{sh(QX)}=\frac{sh \, u}{sh \, w}\). Par \((L_{1a}) \; \; sh \, w = ch \, x \; sh \, u\), il vient \(sin \; \hat{B} = \displaystyle \frac{1}{ch \, x}\),
ce qui donne la relation \((E_2) \; \; \hat{B}=\Pi(SP)\).
• La formule du cosinus dans un triangle rectangle donne \(cos \; \hat{A} = \displaystyle \frac {th(PQ)}{th(QX)}=\frac{th \, u}{th \, w}\). Par \((L_{2b}) \; \; th \, w = th \, u \; ch \, v\), on peut écrire \(cos \; \hat{A} = \displaystyle \frac{1}{ch \, v}\). Or \( \displaystyle \frac{1}{ch \, v} = th v^*\), en utilisant les deux relations déjà vues \( sh x^* =\displaystyle \frac{1}{sh \, x} \) et \( ch x^* =\displaystyle \frac{1}{th \, x} \).
On a donc \(cos \; \hat{A} = th v^*\), ce qui donne la relation \((E_3) \; \; \hat{A}=\Pi(QR^*)\).
• Enfin, Pythagore dans le triangle \(ABC\) s’écrit \(ch(BC) \; ch \, u = ch \, w\), soit \(ch(BC) = \displaystyle \frac{ch \, w}{ch \, u} = \displaystyle \frac{1}{sin \, \sigma}\) en utilisant \(L_{3b}\). Ce qui signifie \((E_1) \; \; \sigma=\Pi(BC)\).
L’équivalence d’existence du théorème
L’illustration de la figure précédente montre que du quadrilatère on passe au triangle trivialement. Dans l’autre sens, depuis le triangle \(ABC\), on construit construit les points \(P\) et \(Q\) tel que \(PQ=AC\). Alors la perpendiculaire à la perpendiculaire à \((PQ)\) en \(Q\) appartenant au pinceau des droites parallèles à \((AB)\). Cela donne les points \(R\) et \(S\) en même temps. Il a d’autres points de vue de constructions à partir de l’angle de parallélisme. Il serait intéressant de trouver un argument constructif depuis ce point de vue.
Illustrations du théorème
On propose deux illustrations, une où l’on part du quadrilatère, puis une où l’on part du triangle
Construction 1 (du quadrilatère au triangle)
On se donne deux points \(P\) et \(Q\), et on construit les perpendiculaires à la droite \((PQ)\) en \(P\) et \(Q\). On se donne un point \(R\) sur celle issue de \(Q\) et on termine … quand il existe, le quadrilatère de Lambert \(PQRS\).
Dans cette figure, on construit, à la règle et au compas, le triangle \(ABC\) à partir de ces trois conditions du théorème : triangle rectangle en \(C\), \(AC=PQ\) et \(AB=RS\) de la façon suivante : étant donné un point \(C\), on construit à l’aide d’une médiatrice et d’une symétrie orthogonale, le cercle (rouge) de centre \(C\) et de rayon \(PQ\). On prend alors un point \(A\) sur ce cercle. On construit de même le cercle (leu) de centre \(A\) de rayon \(RS\).
La perpendiculaire à \([AC]\) en \(C\) coupe ce cercle bleu en un point \(B\). Voyons que l’on illustre bien un sens du théorème de Engel.
Préférer lancer cette figure dans un nouvel onglet (plus grande, plus lisible).
Construction 2 (du triangle au quadrilatère)
Cette fois, on part d’un triangle \(ABC\) rectangle en \(C\). On veut construire le quadrilatère de Lambert \(PQRS\) associé. Par le même procédé que dans la construction 1, depuis un point \(P\) on construit \(Q\) tel que \(PQ=AC\) (cercle rouge ci-dessous), puis le point \(X\) sur la perpendiculaire à \((PQ)\) en \(P\) tel que \(QX=AB\) (cercle vert).
On sait alors que les droites \((RS)\) – à construire – et \((QX)\) sont parallèles. Comme \((RS)\) est perpendiculaire en \(R\) à la droite \(d\), perpendiculaire à \((PQ)\) en \(Q\), il suffit de prendre la perpendiculaire à \(d\) issue du point idéal \(J\) de la droite \((QX)\). Pour ne pas utiliser le point \(J\) (ici utilisé pour aller vite) on peut toujours construire une droite parallèle à \((QX)\) – par exemple celle issue de \(A\) – par le procédé de Bolyaï déjà mentionné, et utiliser la construction (macro-construction vue dans le menu Bachmann) de la perpendiculaire à une droite donnée issue d’un pinceau donné, construction indépendante du type de pinceau.
Dans la figure suivante, on illustre les vérifications numériques qui rendent compte des relations mises en évidence par Engel.
Utilisation du parallélisme de \((QX)\) et \((RS)\) pour construire \(R\) et \(S\).
Préférer lancer cette figure, plus grande, dans un nouvel onglet.
Cette première caractérisation d’un triangle rectangle par un quadrilatère de Lambert sera ensuite étendue et systématiquement étudiée par Liebmann, en 1901, pour aboutir à une construction des triangles rectangles d’angles donnés très opérationnelle. Ce sera l’objet d’un prochain article.