Cette page est un complément aux présentations des constructions sur la pseudosphère par conjugaison avec le modèle de Klein Beltrami (KB dans la suite), et suppose qu’on ait déjà pris connaissance de cette méthode dans la page dédiée.
Nous avons déjà présenté, dans la page d’exploration des pavages du disque de Poincaré, la première génération de pavage à partir du pentagone orthogonal, dans une figure où on peut échanger P(4,5) et P(5,4) puisque le disque de pavage du pentagone orthogonal est le même que celui du carré à 72°.
On se propose donc ici de détailler la construction de ce même pentagone orthogonal sur la pseudosphère, par conjugaison avec le modèle KB. On passe par la conjugaison car nous n’avons pas développé les calculs intrinsèques d’une rotation directement sur la pseudosphère. Il y a plusieurs variantes pour s’y prendre, nous en présenterons deux, une où l’on pilote le pentagone depuis la pseudosphère et l’autre depuis le disque KB.
Dans une première construction, on part d’un point de la pseudosphère qui sera le centre du pentagone, point que l’on envoie sur KB. Nous allons faire toute la construction dans KB, puis le pentagone et son cercle circonscrit seront renvoyés sur la pseudosphère. Ce qui donne ceci :
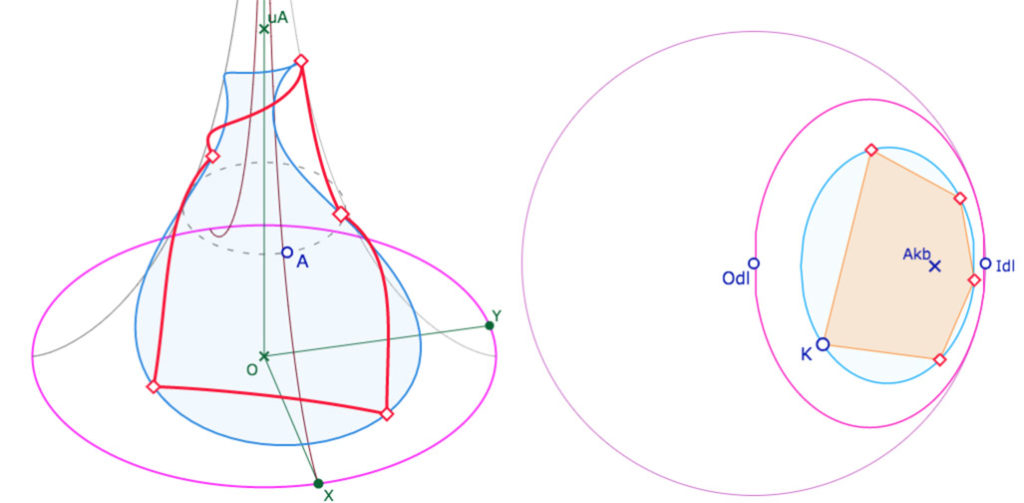
Dans cette construction, le point \(A\), sur la pseudosphère, pilote le centre du pentagone. On peut faire tourner le pentagone sur son cercle circonscrit depuis le point \(K\) du disque de Klein Beltrami.
Construction du pentagone
orthogonal dans KB
Le rayon \(r\) du cercle circonscrit, cercle de pavage de P(5,4) et de P(4,5), sur la pseudosphère, est le même que dans le disque de Poincaré. Il est donné par la relation \(ch(r_{45}) = \displaystyle \frac{1+\sqrt{5}}{\sqrt{10-2\sqrt{5}}}\), ce qui est repris, autrement, par l’expression \(ch45\). ci-dessous. On en déduit le rayon \(r_{45}=ch^{-1}(ch45)\). La distance dans KB étant le double que celle sur la pseudosphère, on sera donc amené à utiliser l’expression \(2r45\).
Le principe de construction est de réaliser le pentagone centré à l’origine \(Odl\) de KB puisque le centre du « disque-limite » de Beltrami est le seul point conforme de tout le modèle : les angles au centre du pentagone y sont les angles euclidiens. De plus un KB-cercle centré en \(Odl\) est un cercle euclidien. On place le projeté \(A_{kb}\)dans KB du point \(A\) de la pseudosphère.
Étape 1
Il faut construire le rayon du cercle centré en l’origine . Il est donné par l’expression nommée \(2r45enO\) qui va permettre de construire le point \(rKB_e\) qui donne un point « euclidien » du cercle circonscrit centré en \(Odl\) dont on sait qu’il est aussi le KB-cercle cherché en \(Odl\) .
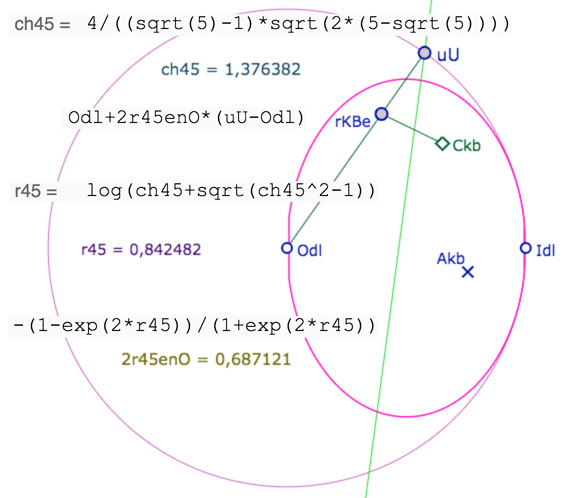
On a construit la KB-médiatrice entre le point \(A_{kb}\) et \(Odl\). Elle coupe le cercle en \(uU\), et c’est sur le segment \([Odl uU]\) que l’on place le point \(rKB_e\) (d’où le signe « – » dans l’expression \(2r45enO\). Le symétrique de \(rKB_e\) par rapport à la KB-médiatrice donne un premier point \(C_{kb}\) du cercle circonscrit cherché. Point que l’on envoie sur la pseudosphère pour construire le cercle associé au pentagone.
Étape 2
On peut donc construire le KB-cercle circonscrit au pentagone orthogonal. Sur ce cercle, on prend un point \(K\) que l’on renvoie en \(s_K\) sur le cercle centré en \(Odl\).
Depuis ce premier point \(s_K\) on construit d’abord, pour l’outil « report d’un angle » \(s_{K_1}\)puis le pentagone régulier par de simples symétries.
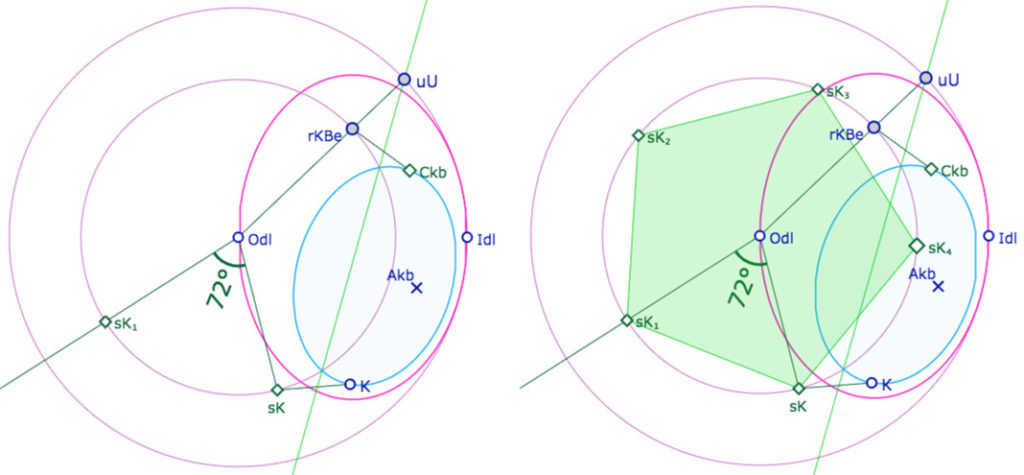
Étape 3
Puis, toujours par symétrie par rapport à la médiatrice, on termine le KB-pentagone régulier qui, par choix du rayon du cercle, circonscrit, est orthogonal.
Étape 4
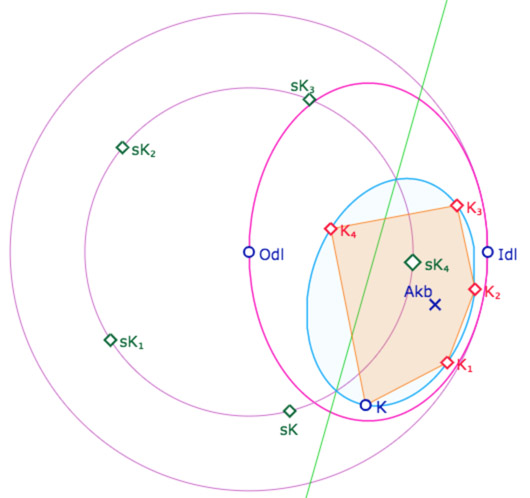
Enfin un première macro-construction transforme les sommets du pentagone en coordonnées \([u_{K_i}, \theta_{K_i}]\) pseudosphériques nommées \(CdK_i\) … que l’on transforme enfin en points pseudosphériques \(LePt_{i+1}\) (décalage de 1 entre les coordonnées et les points de la pseudosphère).
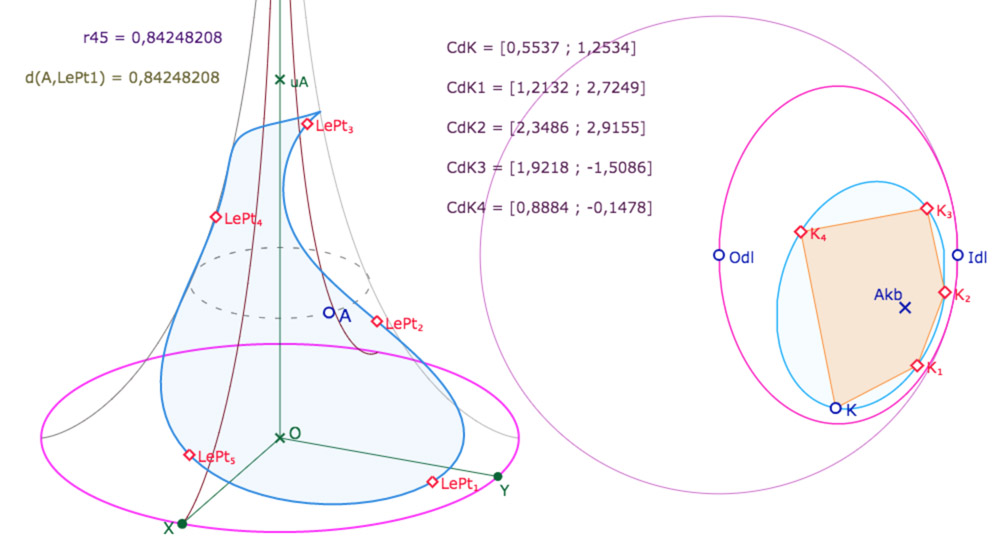
Étape 5
Pour la construction des segments entre ces points nous allons opter pour une méthode qui n’est pas la plus naturelle qui vient à l’esprit En effet, il serait naturel d’utiliser la macro « Segment par coordonnées » pour construire chaque segment depuis ses extrémités. Mais si on fait cela, la figure est très longue à s’ouvrir, au moins 10 min, et selon les ordinateurs jusqu’à 16 min. Alors que si l’on envoie sur la pseudosphère un point de chaque segment du KB-pentagone et qu’on l’on fasse les lieux de ces cinq points, la figure s’ouvre avec un temps d’attente ordinaire, et raisonnable pour ce type de construction. Le construction finale prend alors cette forme
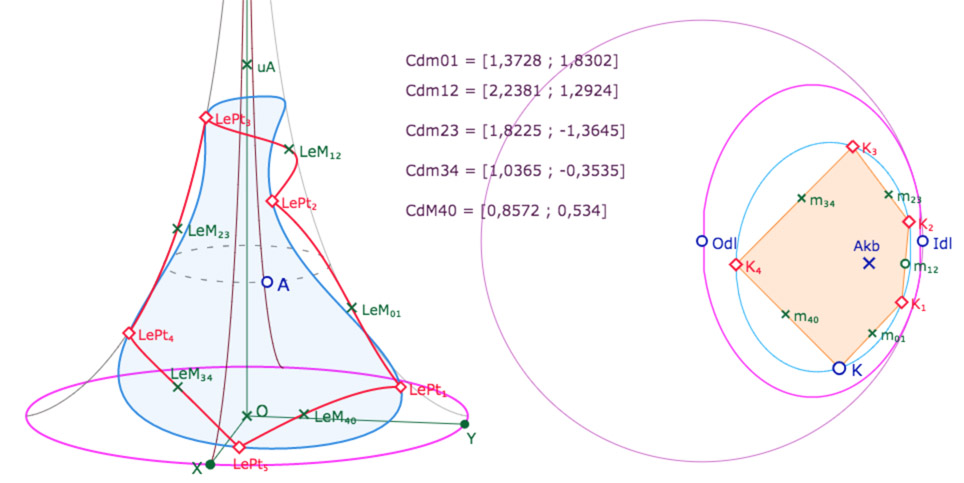
Les points \(m_{ij}\) sont des points « sur objet » des segments du KB-pentagone. On en déduit les coordonnées pseudosphériques \(Cdm_{ij}\) associées et enfin les points \(LeM_{ij}\) sur la pseudosphère … dont on prend les lieux en fonction de \(m_{ij}\).
La figure finale correspondante
On peut manipuler le pentagone orthogonal par son centre \(A\) (ou son altitude \(u_A\)). On peut faire tourner les points du pentagone en agissant sur le point \(K\) dans le disque de Klein Beltrami.
Préférer ouvrir la figure dans un nouvel onglet
Quelques vues sur le pentagone
orthogonal pseudosphérique
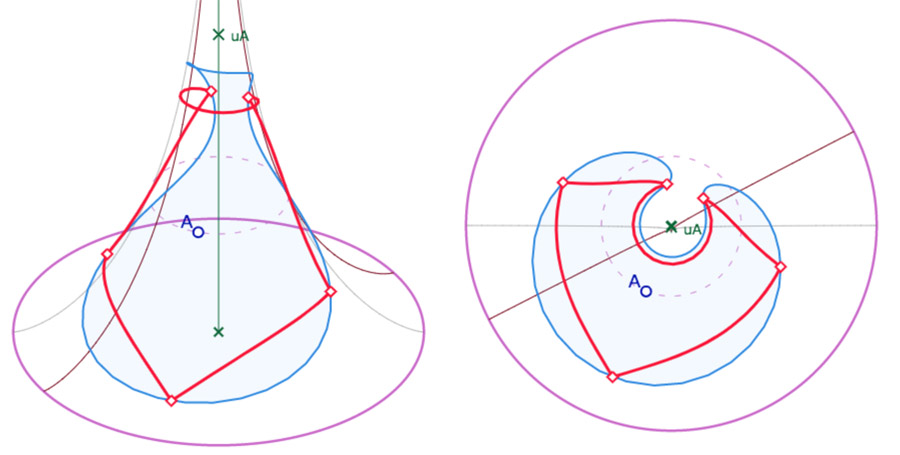
Forme classique du cercle circonscrit « monofeuille » (au sens de « ne dépasse pas l’amplitude d’une feuille ») avec sa vue de dessus
Faire rouler le pentagone orthogonal sur l’équateur frontière de la pseudosphère
On choisit l’altitude de \(A\) pour que le cercle touche l’équateur de la pseudosphère. Alors, en déplaçant \(A\) sur son horicycle, on fait rouler le pentagone sur l’équateur de la pseudosphère et, dans KB, sur l’horicycle limite de la pseudosphère.
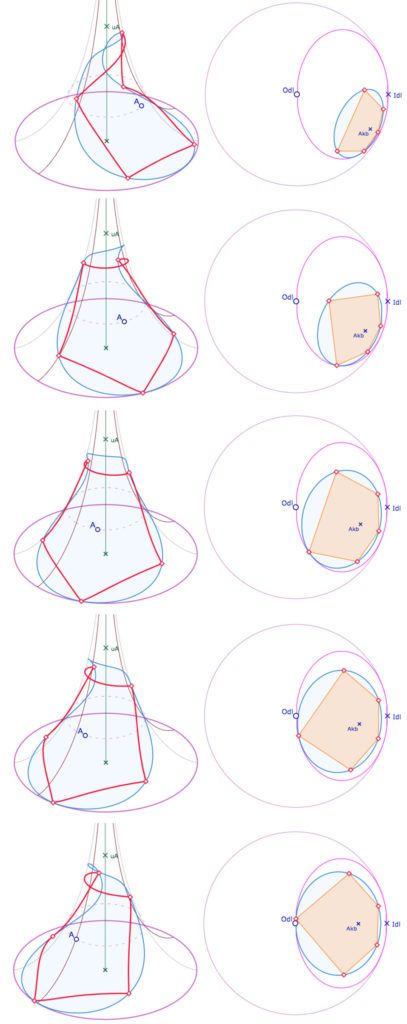
La dernière illustration est l’occasion de signaler que cette figure a été faite avec la feuille principale paramétrée de 0 à \(2\pi\). On a vu dans la page sur les paramètres de conjugaison que cela signifie que le point \(A_{kb}\) est toujours sous le segment \([Odl \, Idl]\). On voit d’ailleurs sur la pseudosphère que le point \(A\) est à la frontière de la feuille principale.
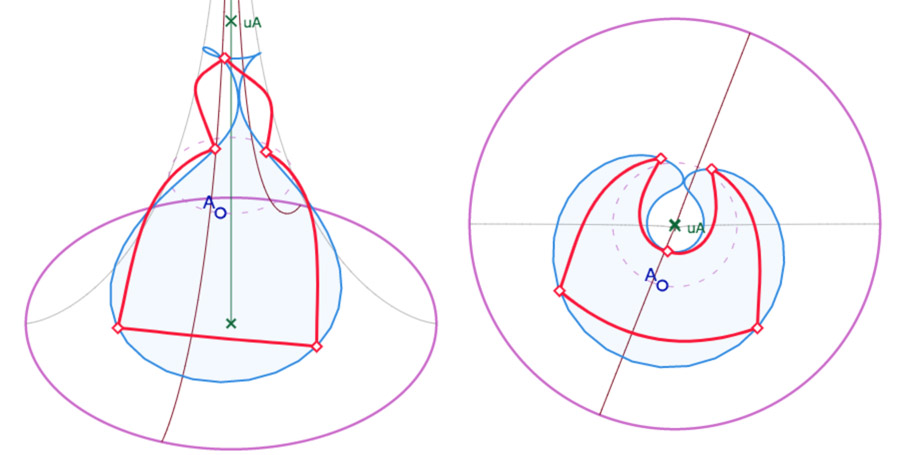
Position du centre du cercle tel que le cercle s’étend sur toute une feuille.
On voit bien le point de contact du cercle avec lui-même dans les deux vues.
Version multifeuille du cercle circonscrit du pentagone orthogonal : en montant l’altitude \(u_A\) le cercle s’enroule sur la pseudosphère, le pentagone orthogonal
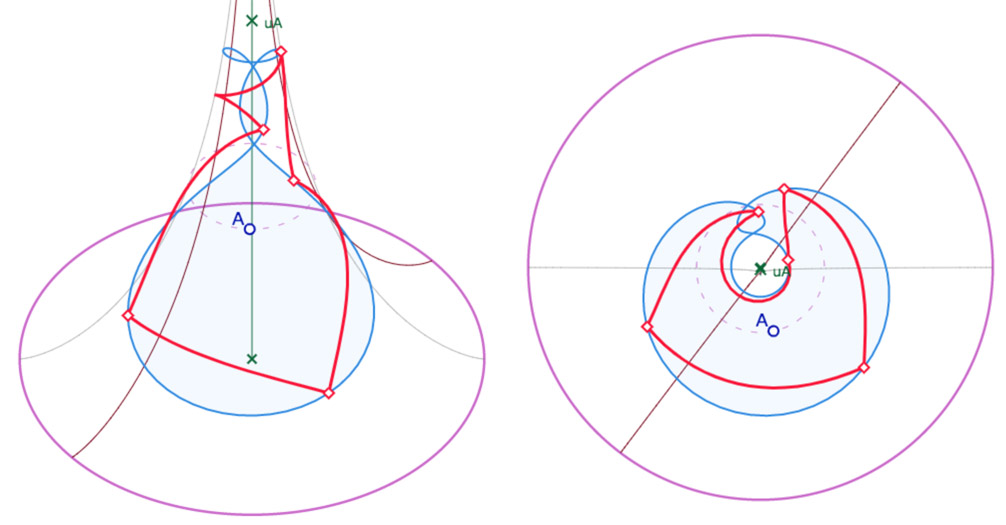
Version « Animation »
Dans cette autre version, on a choisi de construire le cercle circonscrit directement sur la pseudosphère – puisque l’on connait son rayon – ensuite prendre un point de départ sur le cercle (piloté par un curseur sinon on ne peut pas connaitre à la fois l’altitude et la longitude), envoyer le centre et ce point sur KB, faire la construction dans KB, et la renvoyer sur la pseudosphère comme les étapes 4 et 5 précédentes. Cela permet de faire une animation en animant le curseur
On peut déplacer le centre du cercle ou son altitude pendant l’animation mais aussi tourner la pseudosphère.
On peut arrêter l’animation et prendre la main sur le curseur.
On remarquera que la PS-vitesse d’animation augmente ver le milieu du curseur, quand le point d’animation s’approche (un peu plus) de l’infini.
Préférer ouvrir la figure dans un nouvel onglet
Version « pentagone étoilé »
Il est immédiat d’y ajouter la version étoilée
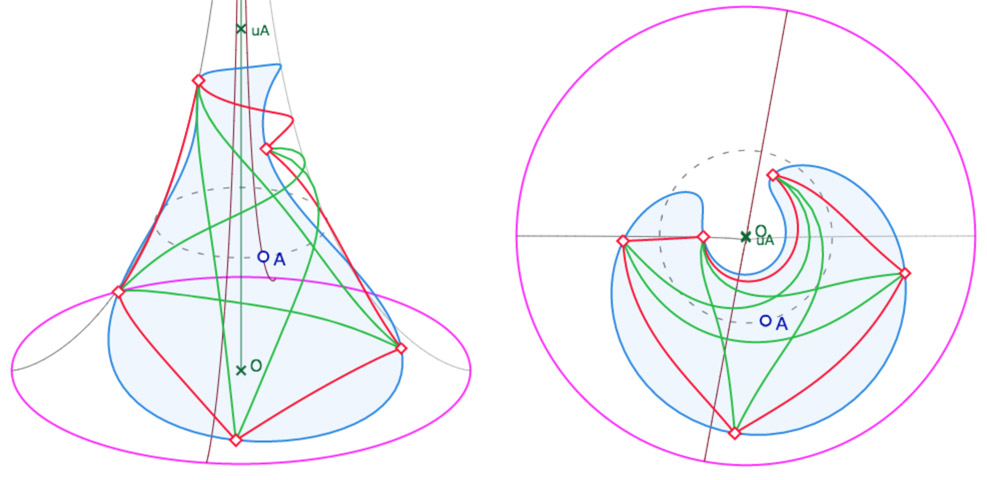
Lancer cette figure dans un nouvel onglet (pentagone piloté pat le point K)
Lancer cette autre version, animée par un curseur, dans un nouvel onglet