Rappel du contexte de la figure
A l’origine du « problème de Malfatti », il s’agit de construire trois cercles inscrits à un triangle (un en chaque sommet) chacun tangent à deux côtés du triangle et tous les trois tangents étant deux à deux.
On a déjà proposé une lecture absolue de la construction traditionnelle, pour l’appliquer d’abord aux modèles bornés de la géométrie euclidienne dont le modèle borné 3D, et ensuite aux géométries non euclidiennes
En particulier nous avons vu, dans le menu sur le disque de Poincaré, l’extension de la construction sur des trilatères : des droites non nécessairement sécantes, qui ne sont pas en faisceau. On a alors présenté une construction en 14 étapes. Pour l’anecdote, à l’étape 12, on avait remarqué que la construction proposée n’était pas fameuse car on a construit un cercle ou une équidistante, selon la configuration, en faisant les deux constructions. Ici, sur la pseudosphère, même si on est toujours en géométrie hyperbolique où les cercles et les équidistantes sont des objets différents, nous verrons qu’une seule construction pour les deux situation va suffire.
Cette page suppose qu’on ait parcouru quelques pages du menu PS en particulier la page d’interlude, sur le modèle KB et les pages suivantes sur la conjugaison
Les options possibles pour la construction sur la pseudosphère
Bien entendu la construction se fait en lien avec le modèle de Klein-Beltrami (KB dans la suite). Il y a alors deux figures générales possibles :
• Soit on part de points de la pseudosphère et on fait la figure par conjugaison. C’est plus dans l’esprit de ce que l’on a proposé dans le menu PS : pour réaliser une figure « en manipulation directe sur la pseudosphère », c’est la seule option possible.
• Soit on part de points de base de KB et on projette ensuite la figure sur la pseudosphère. Cette option est encore « en manipulation directe » mais sur KB plutôt que la la pseudosphère.
En pratique nous proposons les deux car elles vont être réalisées différemment et donc permettront d’explorer la situation de deux point de vue différents. La seconde option est plus manipulable, mais elle prend un peu de temps à charger en ligne.
Un autre choix adopté, pour les deux figures, est de prendre l’option de la plus grande représentation de la feuille principale – ci dessous depuis \(F-\pi\) à \(F+\pi\). Cette modification, précisée dans la page sur la conjugaison, permet une plus grande figure dans le disque-limite de Beltrami DL, mais modifie l’orientation entre la pseudosphère et le plan KB alors qu’elle était respectée avec les macros intrinsèque. Ainsi, quand on fait parcourir l’horicycle d’un point dans le sens trigonométrique par ce point, son image tourne dans l’autre sens sur son horicycle image. En particulier on voit ci-dessous que le trilatère sur DL est inversé : la droite \((A_1 A_2)\) est « à gauche » de la figure sur la pseudosphère, alors que la droite\((A_{1kb} A_{2kb})\) est à droite de la figure sur DL. C’est un point à intégrer pour manipuler rapidement la figure.
La construction par conjugaison
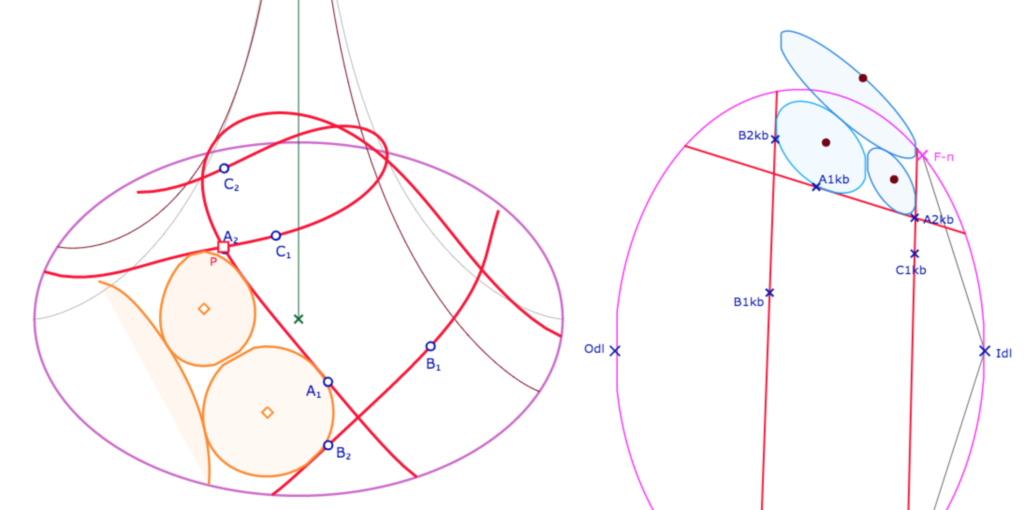
On veut donc construire la figure en partant de points de la pseudosphère. Pour y construire trois droites, on se donne 2 poignées par droites et donc 6 points : \(A_1, A_2, B_1, B_2, C_1, C_2\). Ces points sont envoyés sur le disque-limite de Beltrami en les mêmes points indexés en \(kb\).

Sur la figure, on n’affiche pas le disque limite (DL), trop grand, mais seulement l’horicycle rose dans lequel est contenu la pseudosphère. On prolonge les KB-droites dans le plan euclidien, on construit alors le triangle \(M_{kb}N_{kb}P_{kb}\) qui, avec le vocabulaire de Beltrami, est un triangle idéal. Pour le modèle KB c’est un triangle dans le plongement projectif du plan hyperbolique de KB. On fait alors la KB-construction de Malfatti sur ce triangle idéal, puis on renvoie les cercles sur la pseudosphère.
Sur l’illustration précédente, on voit que \(P_{kb}\) est rentré dans l’horicycle limite rose, et donc que son image \(P\) existe sur la pseudosphère. On parle de « point effectif » dans le menu PS.
Voici une autre illustration
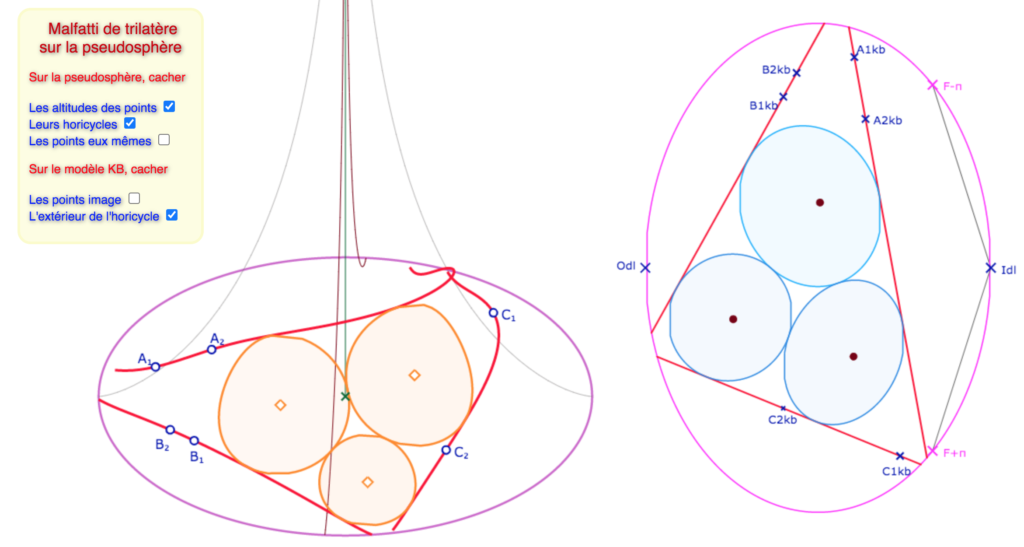
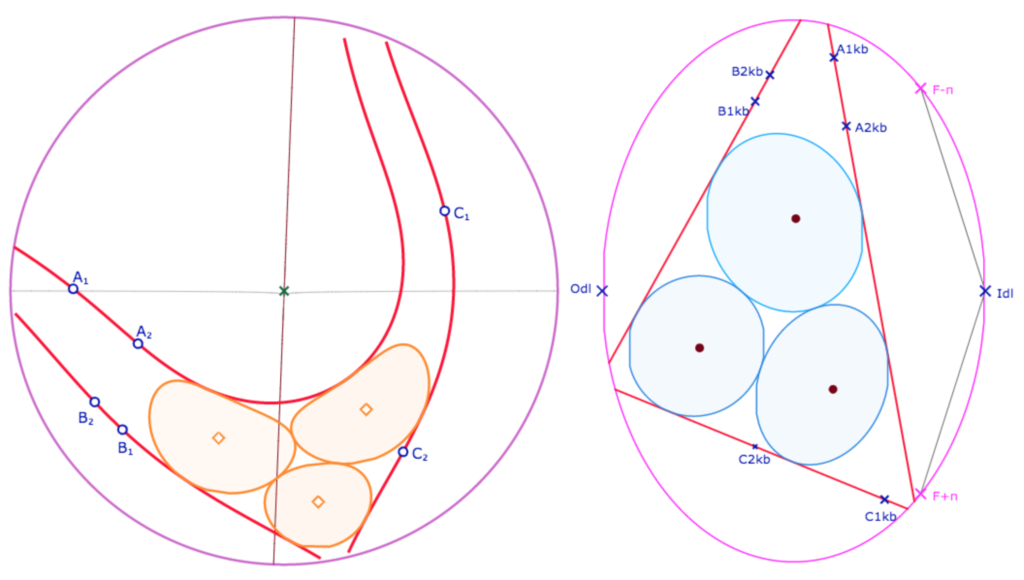
La figure de manipulation
Bien entendu, il faut afficher les altitudes pour modifier significativement la position des points. Pour les horicycles, quand on a l’habitude ce n’est pas utile de les afficher, mais pour une manipulation ponctuelle, cela peut être utile. On n’a pas affiché le repère, pour une question d’esthétique, donc il y a un moment où on franchit la feuille principale ; la longitude passe de \(2\pi\) à 0. Mais on le repère très vite.
La figure est assez grande. Utiliser plutôt le mode « plein écran » de l’iframe
On peut aussi préférer ouvrir pleinement la figure dans une nouvelle page, hors contraintes « responsive » et « figure restreinte »
Un défaut de la méthode utilisée
Dans DGPad, pour le moment, les ellipses ont un défaut de représentation autour d’une partie verticale. Or nous utilisons un point sur l’ellipse, et donc son image sur la PS présente le même défaut de représentation dans certains cas. Pour les illustrations de ces pages, on a évité ces défauts, mais en manipulant la figure on rencontrera ce petit défaut.
Bien entendu, on aurait pu faire autrement, de manière même plus naturelle, sans avoir à tracer les cycles dans KB. Mais bizarrement, la figure devient alors très lente (alors qu’il y a moins de lieu dans la figure) et en pratique inutilisable. D’où cet autre choix. Cela dit, ce choix a un avantage important qui est présenté au paragraphe suivant.
Quand les cercles de Malfatti deviennent des équidistantes
On a déjà utilisé cette figure de KB-construction de Malfatti pour illustrer la façon dont Beltrami met en évidence les équidistantes de son disque-limite : quand le centre d’un cercle devient un point idéal, le cercle devient une équidistante pour le modèle KB dont l’axe est la perpendiculaire commune des droites concernées.
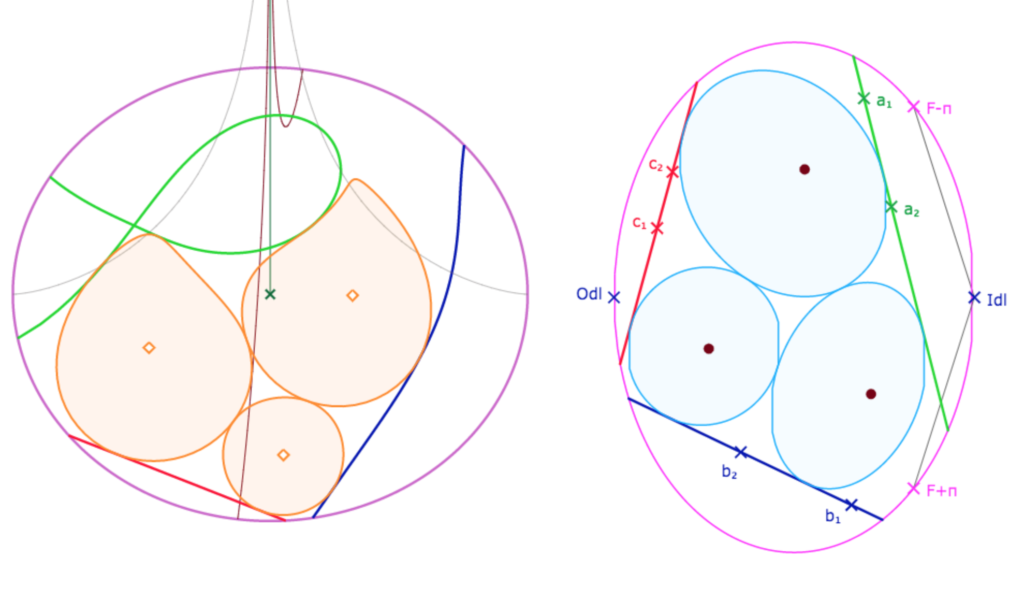
Dans le cas de la pseudosphère – qui n’a qu’un point à l’infini accessible – le point \(L_{dl}\) dans les illustrations, un centre de cercle ne peut sortir de DL que du côté de ce point, au delà des points limites de la feuille principale. Voici ce que cela peut donner :
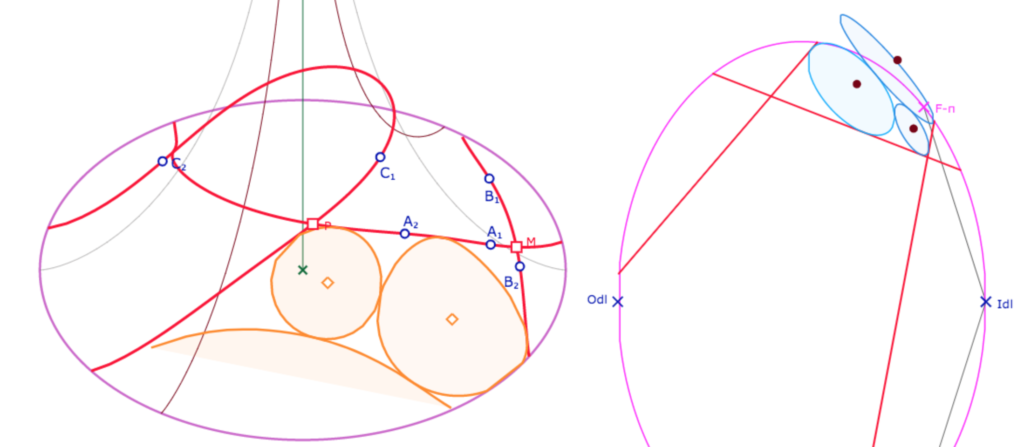
Dans cette illustration, on a donc trois cycles de Malfatti, sous la forme de deux cercles et la trace sur la pseudosphère d’une « équidistante de Malfatti » dont le centre est le point idéal qu’on « perçoit » hors du disque-limite DL sur la partie droite de l’illustration.
Contrairement à ce que l’on a fait dans le modèle du disque de Poincaré, parce que l’on passe par un plongement projectif du plan hyperbolique – et que dans le modèle KB, les trois cycles sont tous représentés par une ellipse – la même construction convient pour les cercles, les équidistantes et les horicycles.
Voici une autre configuration qu’on peut reproduire : dans la première illustration on a trois cercles d’un trilatère proche d’un triangle idéal avec un point idéal très éloigné
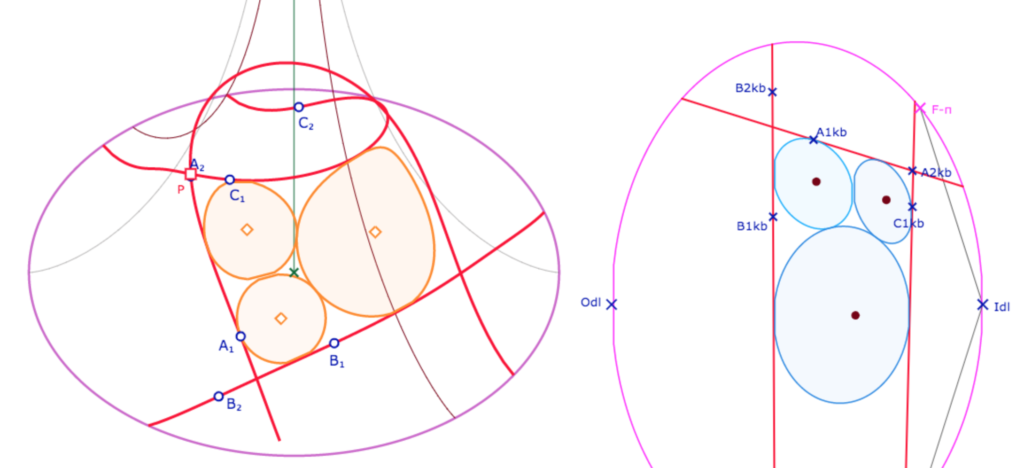
Puis on déplace le point \(B_1\) de quelques pixels sur son horicycle, et le point idéal change de demi-plan par rapport à la droite \((A_{1kb}A_{2kb})\) et un cercle devient une équidistante.
La construction depuis KB
Cette construction est finalement plus simple, et plus manipulable. Elle est un peu longue à charger (environ 15 s). Cela est probablement dû au fait qu’on a choisi cette fois de construire les trois cercles sur la pseudosphère avec la macro intrinsèque à la pseudosphère, depuis les coordonnées obtenues depuis la construction dans KB. L’intérêt est que le tracé va être plus fin et va permettre d’observer d’autres configurations. Par contre, comme on utilise l’existence effective des centres des cercle sur la pseudopshère, ce qui vient d’être fait ci-dessus sur l’équidistante ne peut pas, par construction, être reproduit.
Description succincte de la figure
On part donc de six points \(a_1, a_2, b_1, b_2, c_1, c_2\), à l’intérieur de l’horicycle délimitant la pseudosphère. Ce sont des poignées de trois droites \(a, b, c\) qui se coupent, dans le plan euclidien en trois points que l’on a encore nommé \(M_{kb}, N_{kb}, P_{kb}\) comme à la figure précédente. Une macro donne le centre et un point de chaque cercle de Malfatti du triangle \(M_{kb}N_{kb}P_{kb}\) rapporté au cercle limite DL non représenté ci-dessous car trop grand. Comme dans la figure précédente, la construction des « cercles de Malfatti de trialère » se fait par la construction des cercles de Malfatti d’un triangle « idéal » (en reprenant le vocabulaire propre à Beltrami) du plongement du plan hyperbolique (DL) dans un plan projectif général.
On construit les cercles par leurs centres et points de contact. Par contre on a choisit de construire les droites du triangle directement depuis les droites de KB, par lieu. L’option était de proposer plusieurs options de ces tracés quand une droite s’enroule trop sur la pseudosphère, mais cela n’a pas être retenu car pas encore tout à fait satisfaisant : limiter à la feuille principale peut faire perdre des contacts entre droite et cercle par exemple.
Voici une première illustration assez standard. Les couleurs permettent d’anticiper les manipulations que l’on peut choisir d’effecteur. Par exemple en remarquant que la droite rouge est proche du point \(O_{dl}\), on en déduit que le méridien coupé par la droite rouge sur la pseudosphère est opposé au méridien contenant le point \(X\) du repère (des figures générales du menu PS). En effet, dans ces figures \(X\) est de longitude \(-\pi\), car on est dans l’option où la feuille principale est sur l’intervalle \([-\pi,\pi]\).
Quelques configurations un peu spécifiques
Les configurations qu’on ne pouvait pas correctement illustrer dans la figure précédente sont par exemple celles où un cercle est trop proche du point idéal \(I_{dl}\), le seul point à l’infini accessible à la pseudosphère. Donc quand le cercle s’approche de ce point dans KB, cela signifie qu’il s’enroule plusieurs fois sur la pseudosphère, comme ici par exemple :
On voit bien que la droite verte a son contact avec le cercle enroulé qui reste sur la feuille principale, de même pour la droite bleue, ce qui se voit aussi sur la vue de dessus
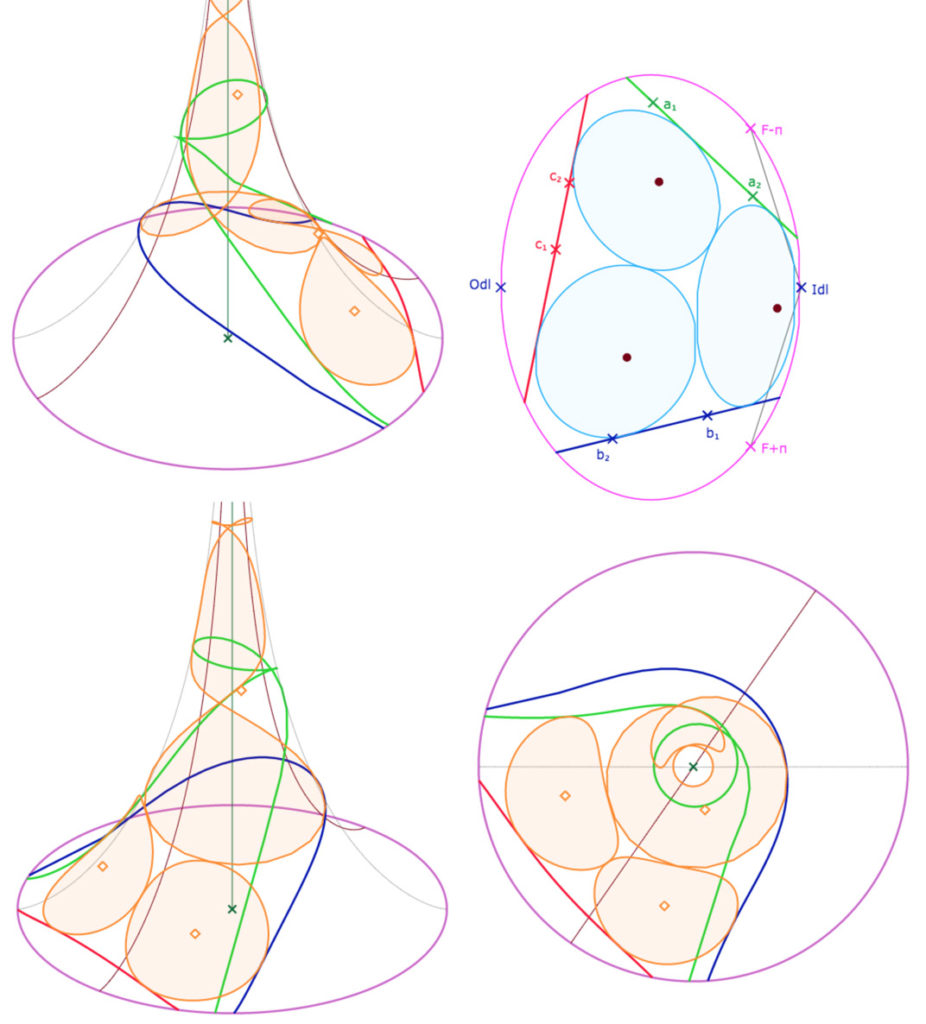
Et on peut aller un peu plus loin, avec un contact sur la feuille précédente à la feuille principale (toujours la droite verte) et donc un cercle encore plus enroulé sur lui-même. Là encore c’est plus clair sur la vue de dessus.

La figure à manipuler
La figure est proposée en mode responsive mais aussi en mode non restreint en plein écran dans une nouvelle page. Pour simplifier le chargement, on a enlevé les macros mais, dans tous les cas, le temps de chargement peut être de l’ordre de 15 s …
Sans entrer dans des détails trop technique, pour que les points « poignées » soient modifiables dans le plan sans être affectés par la rotation de la pseudosphère, ils sont dans un environnement particulier dit « flottant ». Le point repère du la partie plane, le point \(O_{dl}\) aussi. Cela signifie qu’ils sont indépendant. Il en résulte une règle : ne pas jouer à déplacer le point \(O_{dl}\) car cela modifierait toutes les coordonnées des poignées …
La figure est en « mode retreint » pour une utilisation plus naturelle. Utiliser l’icone plein écran de l’iframe
Préférer ouvrir la figure en mode « index » (pleine page) dans un nouvel onglet. Penser à être en « mode consultation » (sans outil) pour pouvoir changer l’orientation de la pseudosphère.
On peut aussi télécharger les deux figures pour une utilisation hors ligne