Dans cet article on poursuit l’exploration des modèle projectifs elliptiques (KE) et hyperbolique (KH) comme introduits dans ce premier article sur les droites. On rappelle qu’à partir du travail de Daniel Perrin (spécifiquement du fichier DPPartie4 qui nous sert de référence), on s’intéresse à des illustrations ou des explorations dynamiques autour de ses résultats.
Dans ce chapitre on aborde l’un des objets essentiels d’une géométrie métrique : les cercles. On verra qu’ils ont des aspects divers, tant en géométrie hyperbolique, où ils ont (au moins) trois apparences selon la position de leur centre : cercles, horicycles, équidistantes, qu’en géométrie elliptique où, selon les modèles, ils peuvent être en plusieurs morceaux. Cela ne manquera pas d’avoir des répercussions sur leurs intersections et donc sur les constructions “à la règle et au compas”.
Daniel Perrin – Partie 4 – Chapitre 7 – page 257
A propos de l’organisation de cet article
Dans cette partie 4 de son ouvrage, Daniel Perrin consacre deux chapitres aux invariants que sont les longueurs et les angles, chapitres qu’il a placé avant celui sur les cercles (ce sont les chapitres 4 et 5). Comme ils sont plus techniques, voire plus conceptuels, nous avons réservé ce thème plutôt à un troisième article. Il en résulte que certains points du chapitre 7 – quelques points sur les distances, mais aussi la puissance d’un point – ne seront abordés qu’ultérieurement.
Premières constructions
On retient de la présentation de Daniel Perrin que le cercle de centre \(O\) passant par \(A\) :
• est le lieu des images de \(A\) dans les symétries orthogonales des droites passant par \(O\) (page 257 avec un vocabulaire de groupe : orbite des stabilisateurs de \(O\)).
• en pratique, ce cercle est représenté par une conique.
• Dans KH, à cause de l’annulation de la forme quadratique sur le cercle unité, un KH-cercle est soit à l’intérieur du cercle unité, soit à l’extérieur, un KH-cercle ne coupe pas le cercle unité, alors que cette restriction ne s’applique pas à KE qui n’a aucun point isotrope.
On peut commencer par une construction naïve en prenant de nombreux symétriques par rapport à des droites passant par \(O\). Ci-dessous dans KE.
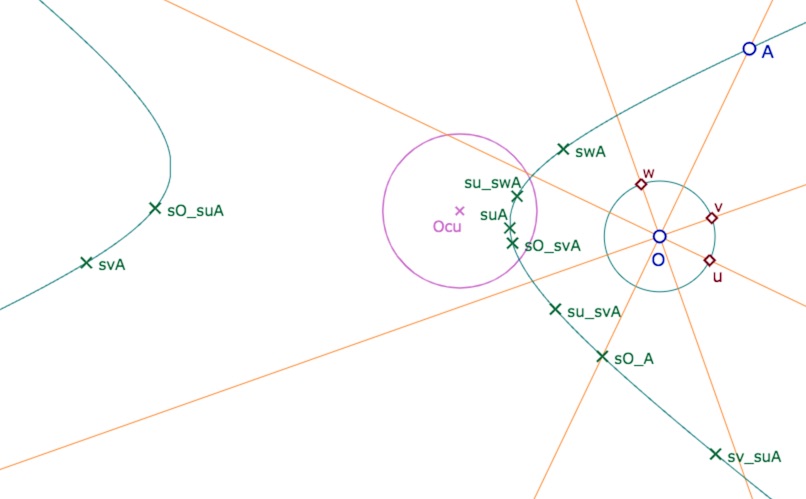
On rappelle que les modèles sont construits à partir d’un cercle dit ‘unité » (toutefois de rayon modifiable
à la souris dans toutes les figures de ces articles) et centre \(O_{cu}\).
\(sxA\) est le KE-symétrique orthogonal de \(A\) par rapport à la droite \((Ox)\)et \(sO_t\) est l’image du point \(t\) par la KE-symétrie centrale de centre \(O\). On construit la conique passant par 5 des 10 points construits. Pour construire une macro des KE et KH cercles, on peut faire bien plus simple car trivialement la droite \((O_{cu}O)\) est aussi un axe de symétrie et, cette droite passant par le centre du cercle unité, les KE et KH orthogonalités sont toutes les deux la symétrie orthogonale euclidienne ce qui va simplifier la construction.
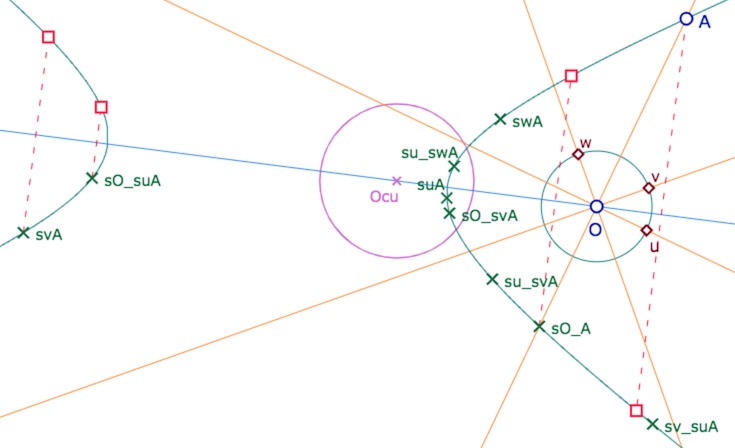
Ci-dessus 4 points (carrés rouges) sont des symétriques euclidiens de points de la coniques
par rapport à la droite des centres \((OO_{cu})\)).
On peut alors commencer à faire deux macros KE-cercle (vert) et KH-cercle (rouge).
Si \(O\) est extérieur au cercle unité, le KH-cercle (le rouge) est bitangent au cercle unité
en les deux points d’intersection de la polaire de \(O\) et du cercle unité.
A priori dans KH ces deux points n’appartiennent pas au KH-cercle. Daniel Perrin parle alors de « conique support » et, propose d’identifier quand même, par abus de langage, le cercle avec sa conique support, ce que nous ferons avec lui.
Préférer ouvrir cette figure dans un nouvel onglet.
Les cas dégénérés
• Il y a tout d’abord le cas où la droite \((OA)\) est tangente au cercle unité – le lieu cercle est réduit à deux droites confondues – privée du point de contact avec le cercle unité dans KH. A priori, dans KH, on ne peut pas dire que c’est une droite car les droites isotropes ne sont pas des droites de KH.
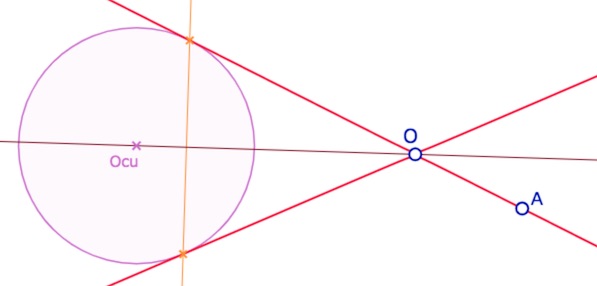
Illustration d’un premier cas dégénéré dans KH.
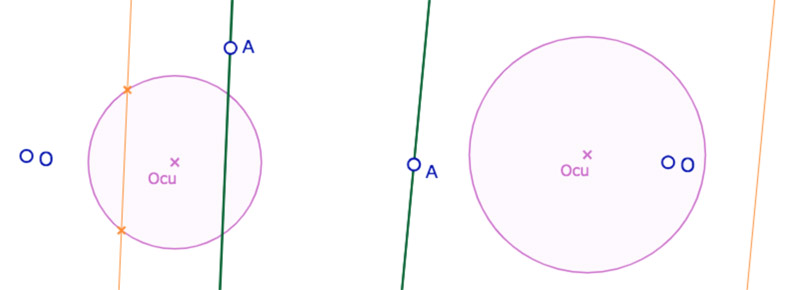
• Il y a ensuite le cas où \(A\) est sur la polaire de \(O\) dans KH, ou la KE-polaire dans KE. Dans ce cas le cercle est une droite, dans tous les cas dans KE, avec une restriction dans KH quand la polaire coupe le cercle unité :
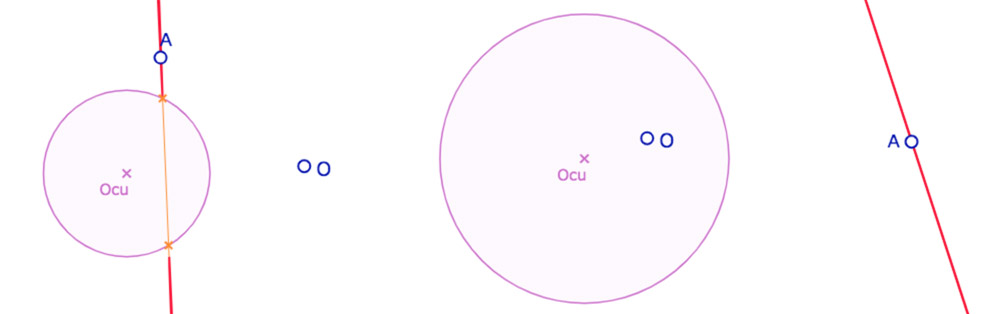
Ci dessus, dans KH, à gauche le cercle est réduit à deux demi-droites, à droite le cercle est toute la polaire de [latex]O[/latex].
Ci-dessous, dans KE, le cercle est toute la KE-polaire dans les deux cas (symétrique de la polaire orange).
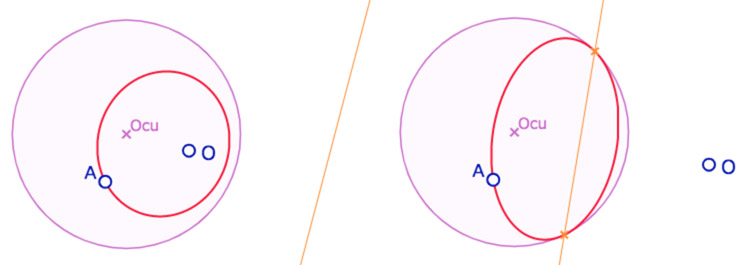
Le cas où A est à l’intérieur du cercle unité
Dans KH, on est sur un cycle hyperbolique. Si le centre \(O\) est lui aussi à l’intérieur du cercle unité, le KH-cercle est bien un KB-cercle c’est-à-dire un cercle hyperbolique du modèle de Klein-Beltrami (illustration de gauche). Si \(O\) est à l’extérieur du cercle unité, le KH-cercle est une ellipse intérieure bitangente au cercle unité : c’est alors une KB-équidistante (illustration de droite). Les points de contact avec le cercle unité sont l’intersection de la polaire du centre \(O\). Cette polaire étant alors l’axe de l’équidistante (au sens de cette présentation du modèle KB.
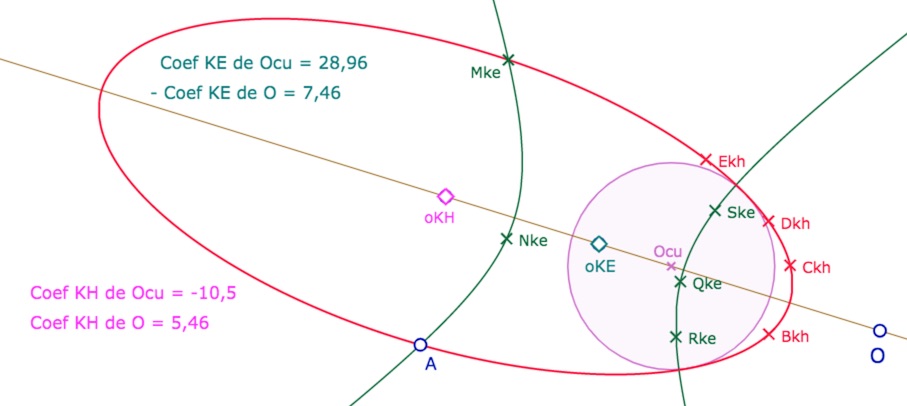
Le centre de la conique associée
Daniel Perrin propose (en exercice, p. 287) les caractéristiques et calculs suivants.
Les calculs sont présentés autrement, on consultera le paragraphe 1.2.4 page 20 pour faire la correspondance avec la version suivante, un peu moins conceptuelle.
Calcul du centre euclidien de la conique associée
Il est bien entendu sur la droite \((O_{cu}O)\) et c’est précisément le barycentre de
• dans KE : \(\left( O_{cu}, q_{KE}(O)q_{KE}(A)-\varphi^2_{KE}(O,A) \right)\) et \(\left( O, -q_{KE}(A) \right)\)
• dans KH : \(\left( O_{cu}, q_{KH}(O)q_{KH}(A)-\varphi^2_{KH}(O,A) \right)\) et \(\left( O, q_{KH}(A) \right)\)
Rappel : avec \(q_{KE}(M)=x_M^2+y_M^2+1\), pour KE, et \(q_{KH}(M)=x_M^2+y_M^2-1\), pour KH, et les formes polaires associées \(\varphi_{KE}\) et \(\varphi_{KH}\) respectivement.
Avec le centre de la conique et l’axe de symétrie (qui n’est pas toujours l’axe focal, ce n’est d’ailleurs jamais le cas dans KB), on pourrait reprendre les premières macros de construction « naïves » des cercles KEKH et les simplifier. Toutefois ces macros ne s’appliqueraient pas pour les cercles représentés par des paraboles.
Cas des coniques de même centre euclidien
La géométrie dynamique permet des explorations originales comme celle de ce paragraphe. Dans la figure suivante on explore les possibilités pour que les deux coniques représentant les KE et KH cercles de centre \(O\) passant par \(A\) aient même centre euclidien. Plus particulièrement, pour \(O\) donné, on cherche des positions de \(A\) pour que les deux coniques aient même centre.
• à l’ouverture, le point \(A\) est tel que les deux centres \(o_{KH}\) et \(o_{KE}\) soient, visuellement, confondus. On se propose de réaliser une construction ou les deux centres sont « réellement » (mathématiquement) confondus. On le fait sur un cas particulier, juste pour illustration.
• Pour cela, le point \(A\) est aimanté légèrement, à 10 pixels, au cercle vert, de rayon \(CU \sqrt{3}\) où \(CU\) est le rayon du cercle unité. En effet sur ce cercle, on a \(q_{KE}(A)=4\) et \(q_{KH}(A)=2\), soit le premier le double de l’autre.
• On cherche alors les conditions pour les deux autres coefficients soient eux aussi le double l’un de l’autre, au signe prés bien entendu.
• On trouve alors deux droites parallèles. Chacune de ces deux droites, pour \(O\) un peu éloigné du cercle vert, coupe ce cercle vert en deux points. Il y a donc 4 solutions \(a_1, a_2, a_3, a_4\) pour que les centres des coniques soient confondus. Et ceci uniquement pour ce cas particulier de la ligne de niveau \(q_{KH}(A)=2\) et \(q_{KE}(A)=2q_{KH}(A)\).
• Dans cette figure \(A\) est aimanté à 10 pixels par le cercle vert, et à 20 pixel pour les 4 points solution \(a_1, a_2, a_3, a_4\). Commencer par placer \(A\) sur les points solutions.
• On peut aussi déplacer \(O\) autour du cercle vert, à l’extérieur.
• Si on le place à l’intérieur, une droite peut disparaître. Relancer alors la figure par l’icone de rechargement dans l’iframe.
• On remarquera que les coefficients barycentriques de A sont les mêmes en \(a_1\) et \(a_2\). Idem pour les points \(a_3\) et \(a_4\)
Préférer lancer cette figure dans un nouvel onglet. Elle est plus grande, et on a laissé visibles tous les calculs intermédiaires (Manipuler la figure dans le mode consultation – aucun outil sélectionné – et explorer les données algébriques dans le mode expression – icone calculatrice activée).
On a développé cette figure essentiellement pour illustrer cette propriété : quand les cercles KE et KH – de centre O passant par A – sont représentées par deux coniques de même centre, elles ont aussi les mêmes foyers (ici seulement illustré, cela ne devrait pas être difficile à montrer).
Dans cette figure, placer \(A\) sur l’une des 4 solutions, et vérifier que les foyers sont confondus :
leur distance devient nulle. Penser à déplacer le point \(O\).
Le type de conique représentant le cercle
Dans le même exercice (p 287), il est proposé [toujours sous une autre forme] cette caractérisation :
La conique représentant le cercle de centre \(O\) passant par \(A\) est une ellipse, une parabole ou une hyperbole selon que l’expression
• pour KE : \(q_{KE}(O)q_{KE}(A)-\varphi^2_{KE}(O,A)-q_{KE}(A)\) et
• pour KH : \(q_{KH}(O)q_{KH}(A)-\varphi^2_{KH}(O,A)+q_{KH}(A)\)
• est, respectivement, négative, nulle ou positive.
Ce qui donne, par la même occasion, l’équation cartésienne de l’unique cercle de centre \(O\) représenté par une parabole. Voici par exemple les coordonnées du sommet et de deux autres points de l’unique parabole qui est un KE-cercle de centre \(O\) (deux points dont on prend ensuite les symétriques par rapport à la droite des centres).
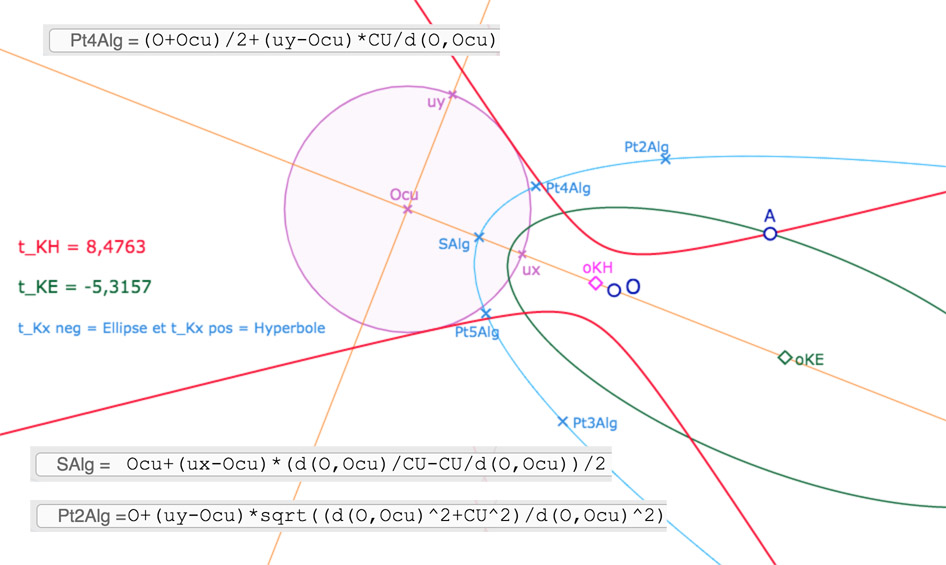
En dehors du sommet, on a choisi comme points de la parabole celui « au dessus » de \(O\), et « au dessus » du milieu de \(O\) et \(O_{cu}\). On en verra l’intérêt à la figure suivante.
Par ailleurs, l’unique parabole représentant un KH-cercle de centre \(O\) est le symétrique de la parabole pour le KE-cercle (bleue ci-dessus) par rapport à la médiatrice euclidienne de \([OO_{cu}]\), ci-dessous la parabole verte.
Manipulation de la figure
Le comportement des paraboles de DGPad ne permet pas une aimantation stable du point \(A\) par les deux paraboles. On a donc choisi une autre construction des paraboles, géométrique, et surtout sous forme de lieu. Cette construction est détaillée dans un autre article consacré aux « cercles-paraboles ». L’aimantation est bien plus précise. On a conservé les deux points \(Pt_4Alg\) et \(Pt_5Alg\), communs aux deux paraboles. \(A\) est aimanté par les deux parabole à 20 pixels. et par les points \(Pt_4Alg\) et \(Pt_5Alg\), à 5 pixels.
- Manipuler le point \(A\) pour voir le passage par la parabole entre un cercle « ellipse » et un cercle « hyperbole ».
- On peut approcher \(A\) d’une parabole pour voir (une fois aimanté) le coefficient associé devenir nul.
- Placer \(A\) sur l’un les deux points d’intersection des paraboles. Alors les deux coefficients \(t_{KE}\) et \(t_{KH}\) sont simultanément nuls.
- Penser à placer aussi \(O\) à l’intérieur du cercle unité.
Préférer ouvrir cette figure dans un nouvel onglet.
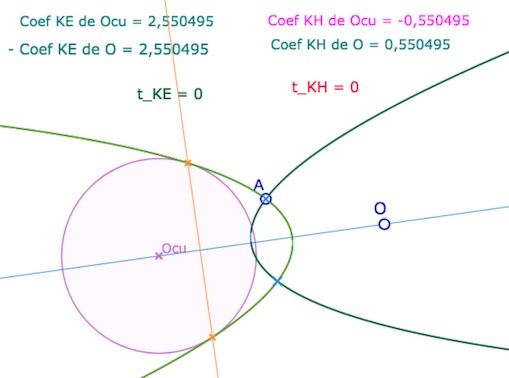
Le cas où \(A\) est sur une des intersections des deux paraboles.
Intersection de deux cercles
Dans KE comme dans KH, l’intersection d’un cercle et d’une droite ne présente aucune difficulté particulière : tout se passe comme on s’y attend. Pour les cercles, c’est plus intéressant, même si on ne sera pas surpris du résultat si on a déjà exploré le menu ELL et en particulier la page sur les cercles.
Dans cette section, on évacue les cas particuliers (voir le paragraphe 7.2.9. p 269) comme les cercles dégénérés en une droite tangente au cercle unité ou le point su la polaire du centre, pour ne traiter que le cas générique où les cercles sont représentés par des coniques propres.
Dans cette situation, l’intersection de deux cercles peut être de aucun à quatre points, en général, avec des situations générales spécifiques. Ainsi, dans KB, c’est-à-dire, à l’intérieur du cercle unité, on retrouve le contexte hyperbolique : les cercles n’ont – au plus – que deux points d’intersection. Voici quelques illustration du cas général, dans chaque modèle, des cercles sans intersection et d’autres avec 4 intersections.
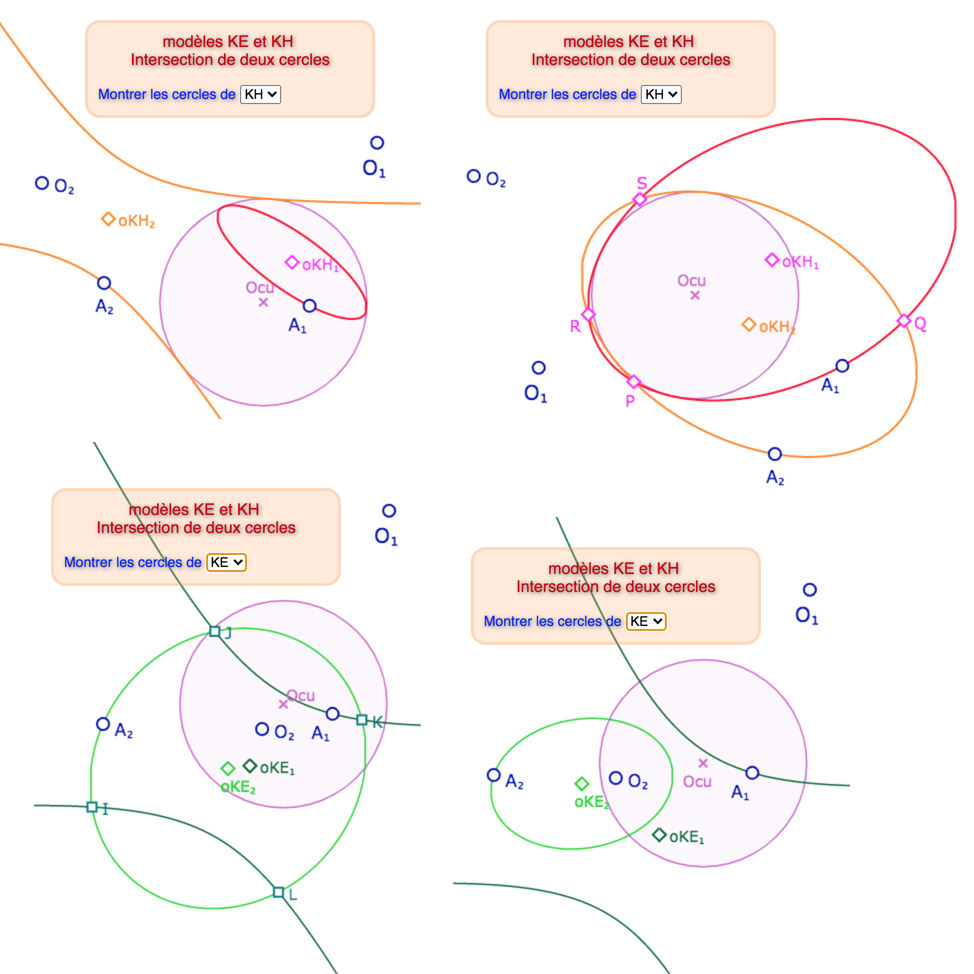
Manipulation de la figure
Préférer ouvrir cette figure dans un nouvel onglet.
Cas particulier de l’intersection des cercles C(O,A) et C(A,O)
La figure suivante illustre la partie elliptique de cette proposition de Daniel Perrin :

Copie d’écran d’un extrait de la page 271 du fichier DPPartie4
Dans la figure suivante, on anticipe un peu sur le prochain article (en utilisant l’invariant I, prélude à la longueur) pour illustrer, de manière « pré-métrique », que les quatre intersections produisent quatre triangle équilatéraux.
Déplacer les points \(O\), \(A\) mais aussi le centre du cercle unité \(O_{cu}\).
On rappelle que, dans un logiciel de géométrie dynamique respectant le déterminisme, la continuité des intersections de deux coniques ne peut pas être toujours respectée. Cela signifie que les intersections peuvent s’échanger entre elles et perturber la figure.
Préférer ouvrir cette figure dans un nouvel onglet (pour avoir une feuille plus grande).
Le cas des horicycles de KH
On a vu que dans KH les cycles peuvent être (aussi) des cercles ou des équidistantes pour le modèle KB, le modèle hyperbolique à l’intérieur du cercle unité. Un type de cycle hyperbolique n’est pas encore abordé, c’est celui des horicycles, c’est-à-dire le cas où le point \(O\), le centre du cercle étudié, est un point du cercle unité. Cette situation est en effet exclue a priori dans ce qui précède car les points du cercle unité ne sont pas des points du « plan hyperbolique étendu KH« . Il faut donc une définition étendue du cercle. Voici un résumé de l’étude Daniel Perrin sur le sujet. (\(\Gamma\) est le nom donné du cercle unité de référence)
Nous allons étendre la définition des cercles \(C(a,b)\) au cas où les points \(a, b\) peuvent être isotropes. L’exercice 4.7.4 montre qu’il faut adapter l’idée initiale dans ce cas. En effet, le groupe des isométries qui fixent un point isotrope est trop transitif. […]
L’ensemble des points \(m\) vérifiant les conditions précédentes est appelé horicycle de centre \(a\), passant par \(b\), et il est noté \(H(a,b)\). Il est égal à la conique \(V(P_{a,b})\) privée du point \(a\). […]
Remarques.
1) Dans le cas \(q(b)=0\), avec \(b=a\), \(V(P_{a,b})\) est égal à \(\Gamma\).
2) Dans le cas \(\varphi(a,b)=0\), avec \(b\) non isotrope, \(V(P_{a,b})\) est la polaire de \(a\), c’est-à-dire encore la tangente en \(a\) à \(\Gamma\) (définie par \(\varphi(a,m)^2=0\) donc une droite “double”). […]Soit \(a\) un point de \(\Gamma\) et b un point non isotrope et non orthogonal à \(a\). La conique \(V(P_{a,b})\) contenant \(H(a,b)\) est une conique propre, surosculatrice à \(\Gamma\) en \(a\). Toute conique surosculatrice à \(\Gamma\) en \(a\), privée de \(a\), est un horicycle de centre \(a\).
Daniel Perrin – Partie 4 – Chapitre 7 – page 272 à 274
En pratique, il n’y a pas de surprise par rapport à ce que l’on a pu voir dans les différents menus du site. La seule nouveauté est que, comme on travail dans le « plan hyperbolique étendu », l’horicycle peut être une conique extérieure au cercle unité alors que, dans les différentes présentations qu’on en a donné, l’horicycle était intérieur au « cercle horizon ».
Horicycles dynamiques
On a dû reprendre la construction des KH-cercles pour que la construction fonctionne quand le point \(O\) est sur le cercle unité. Les figures précédentes ne fonctionneraient pas.
• Le point O est seulement aimanté par le cercle unité (à 20 pixels), on peut l’en extraire.
• On a laissé le KE-cercle vert associé pour voir qu’il n’y a pas de problème particulier
• Remarque 1 : si on place \(A\) sur le cercle unité, la conique devient le cercle unité, on ne parle pas d’horicycle dans ce cas.
• Remarque 2 : Quand on place \(A\) (visuellement) sur la tangente au cercle unité en O, on voit l’horicycle devenir une droite double.
• De même, on peut placer (visuellement encore) \(A\) sur le KH-horicycle « parabole », la construction générique rouge recouvre bien la parabole.
Préférer ouvrir cette figure dans un nouvel onglet.
En utilisant cette figure, ne pas aimanter \(A\) par l’horicycle parabole vert. En effet, la conique du KH-cercle a été reconstruite en utilisant le cercle euclidien de la conique et donc ne fonctionnera pas sur le cas de la parabole.
Il y aurait encore quelques généralités à présenter sur les cercles de KE et KH. Cela est reporté à un prochain article. On termine celui-ci par la finalisation des cercles circonscrits et exinscrits, déjà bien préparés avec l’étude des médiatrices et des bissectrices dans l’article de présentation de KE et KH.
Les cercles circonscrits d’un triangle
Daniel Perrin rappelle très tôt dans sa partie 4, cette propriété aussi élémentaire que fondamentale de la géométrie projective munie d’une orthogonalité : trois points sont alignés si et seulement si leurs polaires sont concourantes. Il précise même :
Cette remarque utilise fondamentalement le fait que q est non dégénérée. Il n’y a rien de tel sinon (notamment en euclidien). C’est ce qui justifie que nous traitions séparément le cas euclidien d’une part et les cas elliptique et hyperbolique d’autre part.
Partie 4 – page 27
Il en résulte que les centres des cercles circonscrits, point de concours des médiatrices, sont tout simplement les polaires des droites des milieux. On reprend une figure du premier article sur KEKH, celle relative aux milieux des points. Et on poursuit. On peut même ne pas utiliser les macros de cercles. En effet, ayant les centres de cercles circonscrits, on peut utiliser seulement le fait que les cercles sont représentés par des coniques. Comme on dispose des trois sommets et du centre, on peut prendre les symétriques de ces points par rapports aux centres : on a 6 points du cercle. Avec macro « conique passant par 5 points », on peut tracer la conique et vérifier qu’elle passe par le sixième point.
Voici quelques illustrations
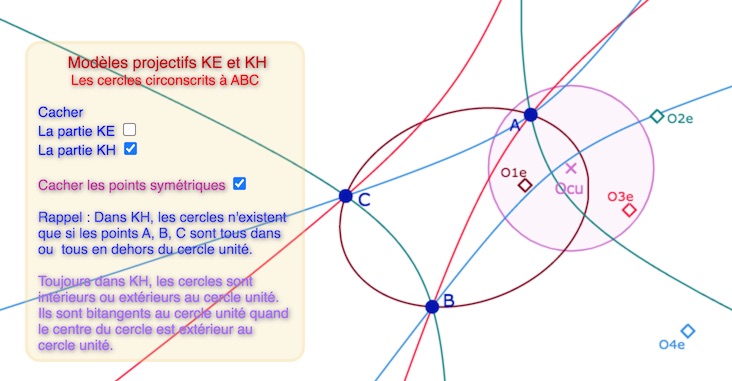
Cas KE (le plus simple) – Les 4 cercles circonscrits à \(ABC\) avec \(A\) à l’intérieur du cercle unité.
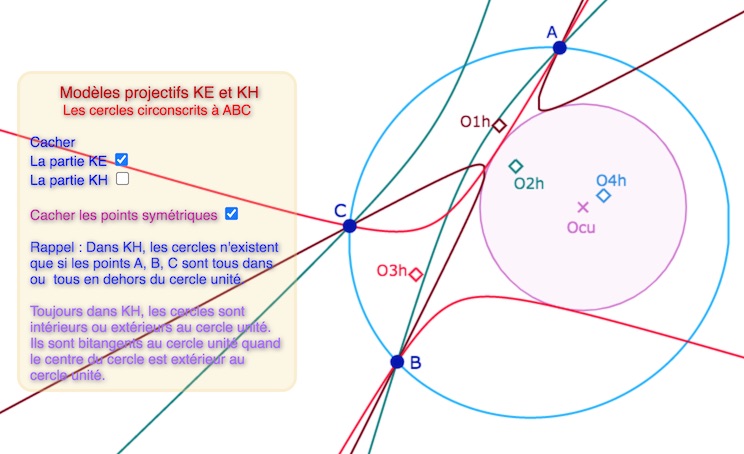
Cas KH – Avec 3 points extérieurs au cercle unité- Les 4 cercles circonscrits sont des hyperboles.
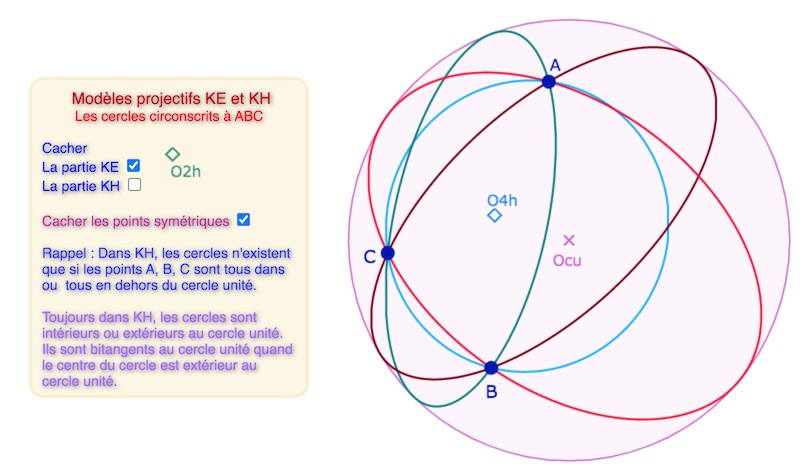
Cas KH – Avec le triangle intérieur au cercle unité – Les 4 cercles circonscrits dont un seul (de centre \(O4_h\)) est LE KB-cercle.
Les trois autres cercles bitangents sont, dans le vocabulaire de KB, des équidistantes. Le centre du cercle est alors le pôle de l’axe de l’équidistante, axe qui passe par les deux points de contact entre la conique et le cercle.
Lancer cette figure dans un nouvel onglet.
Dans cet autre article, on construit des triangles qui admettent un cercle circonscrit représenté par une parabole.
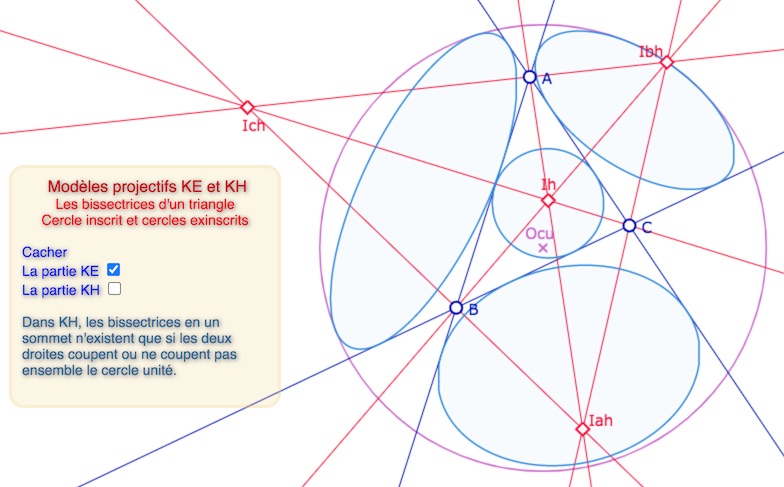
Cercles inscrit et exinscrits d’un triangle
Là encore, on reprend la partie de la présentation de l’article précédent sur les droites où l’on a tracé les bissectrices. Il est lors très simple de poursuivre avec les cercles associés.
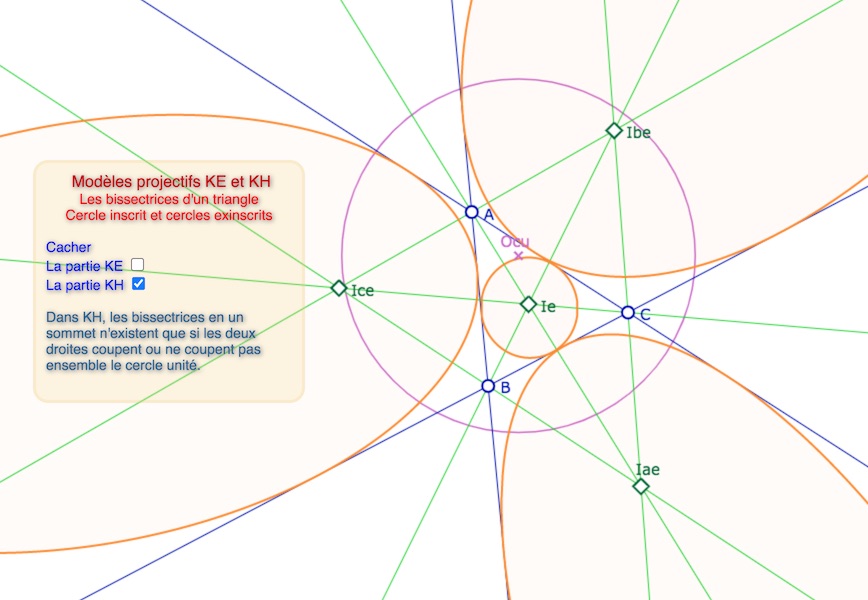
Cercles exinscrits dans KE – Ci dessus ce sont tous des ellipses – Ci dessous avec des hyperboles
Dans l’article 2b-« cercles-paraboles » on s’intéresse à la « frontière » entre ellipse et hyperbole. Par exemple, en fin d’article, étant donné un triangle \(ABC\), on construit un cercle unité pour que les cercles exinscrits soient trois paraboles. C’est actuellement rédigé pour un triangle particulier mais serait généralisable.
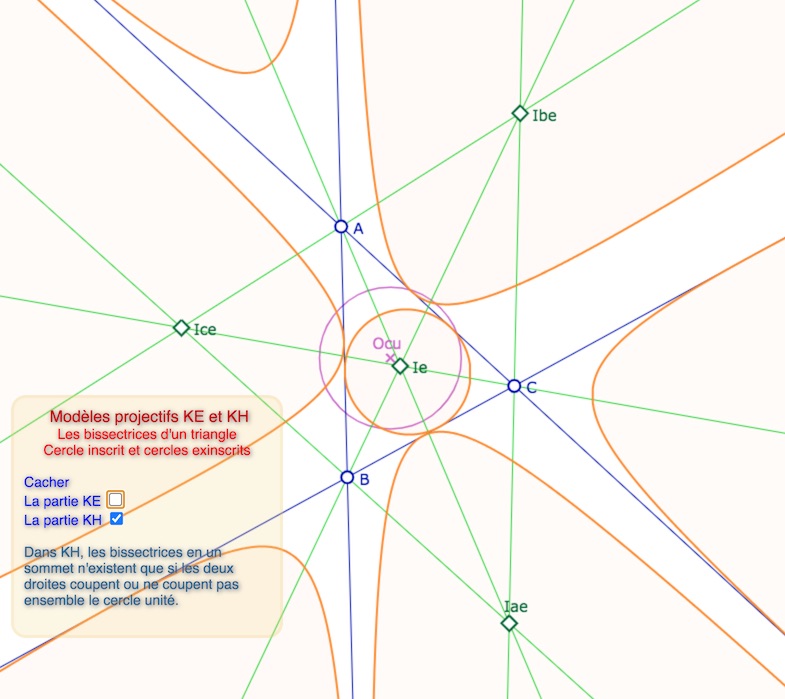
KH est un peu plus classique, mais offre tout de même des configurations intéressantes. On commence par retrouver la situation ordinaire de KB : un cercle inscrit et un exinscrit, une équidistante exinscrite, et (approximativement) un KB-horicycle sur lequel on reviendra car a priori \(Ib_h\) ici est un point isotrope donc pas un point de KH.
Cercles exinscrits dans KH – Ci dessus situation classique de KB, avec un cercle, un horicycle et une équidistante
Ci-dessous avec des exinscrits sous forme d’hyperbole
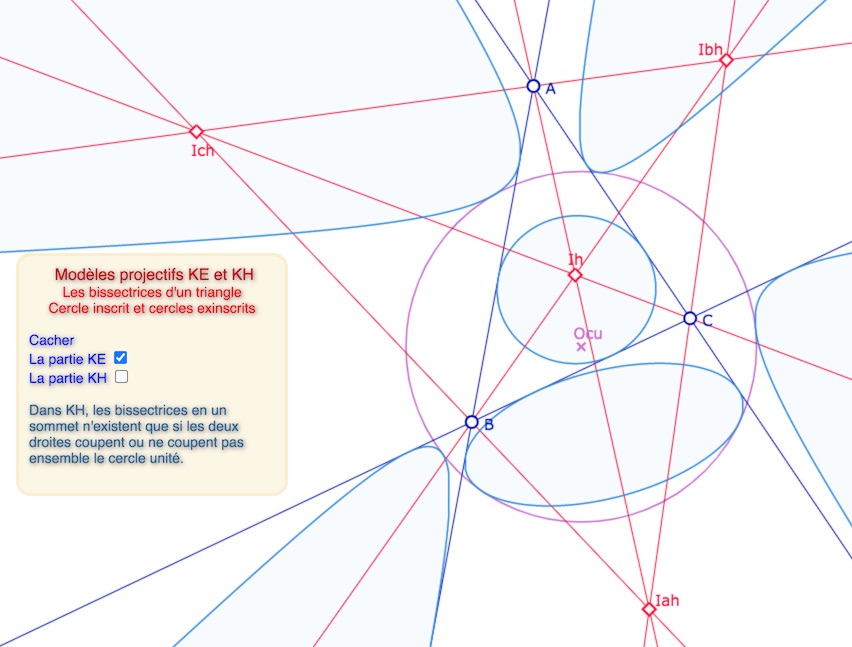
Ci-dessous, une situation un peu plus originale, puisque les contacts des cercles exinscrits
de centre Ibh et Ich ne sont pas sur les côtés du triangle
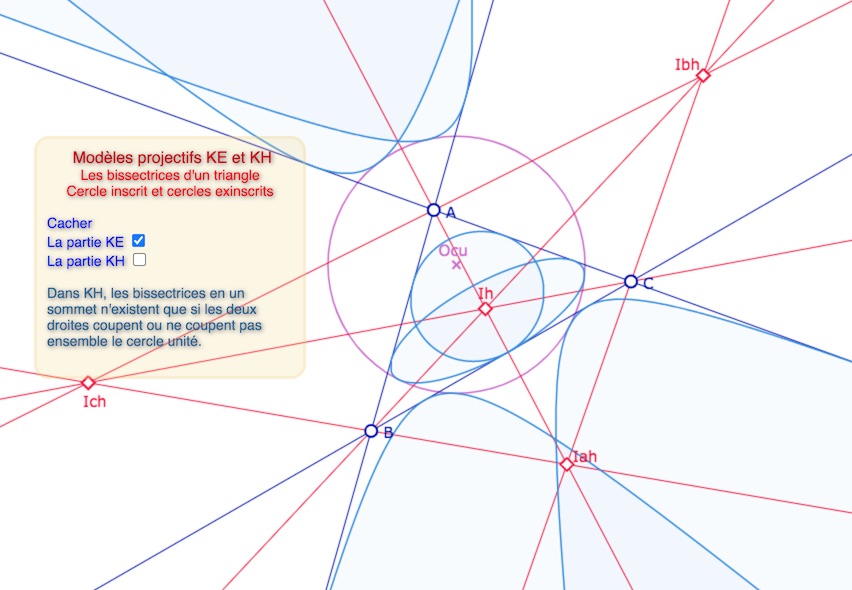
Lancer la figure associée dans un nouvel onglet
On observera l’inversion des noms des centres des cercles : cela signifie qu’il y a un travail à faire sur la notion de bissectrice intérieure ou extérieure, dont on propose un premier traitement dans la section suivante.
KE et KH constructions de Malfatti
et variantes
Jusqu’ici, la notion de triangle utilisée s’applique uniquement pour trois points ou trois droites (trilatères) mais pas trois segments, car nous n’avons défini la notion de segment (sera fait dans l’article 4 non encore rédigé).
Construction dans KE
Nous allons donc utiliser, dans un premier temps, la notion affine de segment pour préciser les bissectrices intérieures et extérieures, quitte à revenir dessus ultérieurement. Cela permet de préciser la notion de bissectrice intérieure comme dans cette figure :
La notion de bissectrice intérieure issue de \(A\) utilise le segment affine \([BC]\)
pour rendre compte du « entre les droites ».
La construction est finalisée, comme souvent dans ce site, par une simple utilisation de isNaN.
Préférer ouvrir cette figure dans un nouvel onglet
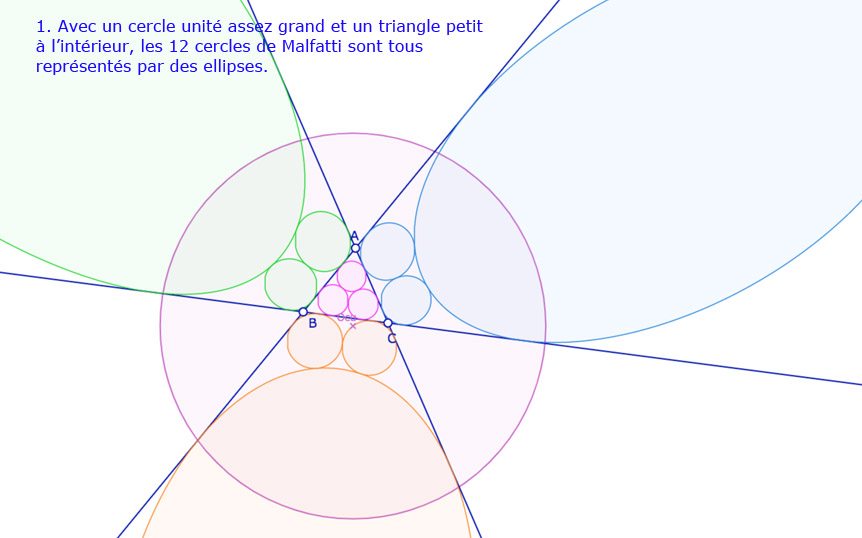
Cette construction étant transformée en macro, en l’utilisant à chaque étape comme décrit plusieurs fois dans ce site, dont ici on arrive à cette première version de la construction de Malfatti dans KE, qui sans être totalement elliptique , est déjà bien sympathique.
Dans cette figure, faire tourner le centre du cercle unité \(O_{cu}\) autour du triangle, modifier son rayon,
et bien entendu déplacer les sommets du triangle.
Cette figure n’est pas « totalement » elliptique car il faudrait aussi construire les cercles de Malfatti « extérieurs » au triangle. C’est ce que l’on se propose d’aborder au prochain paragraphe.
Préférer ouvrir cette figure dans un nouvel onglet.
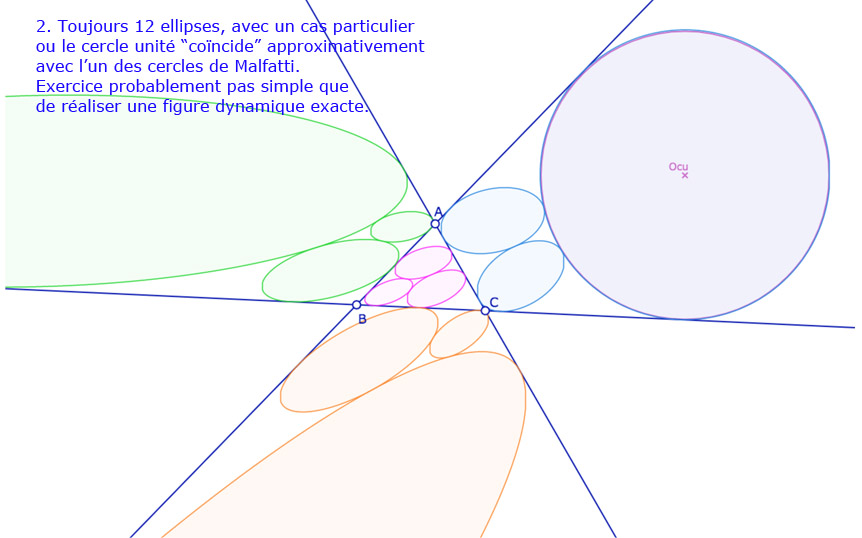
Une construction réellement elliptique de Malfatti
En effet, la géométrie elliptique étant bornée, il est naturel de construire les cercles de Malfatti dans les 3 autres régions (regroupées par deux) définies par les trois droites. Voici un aperçu que ce que l’on peut obtenir avec la prochaine figure.
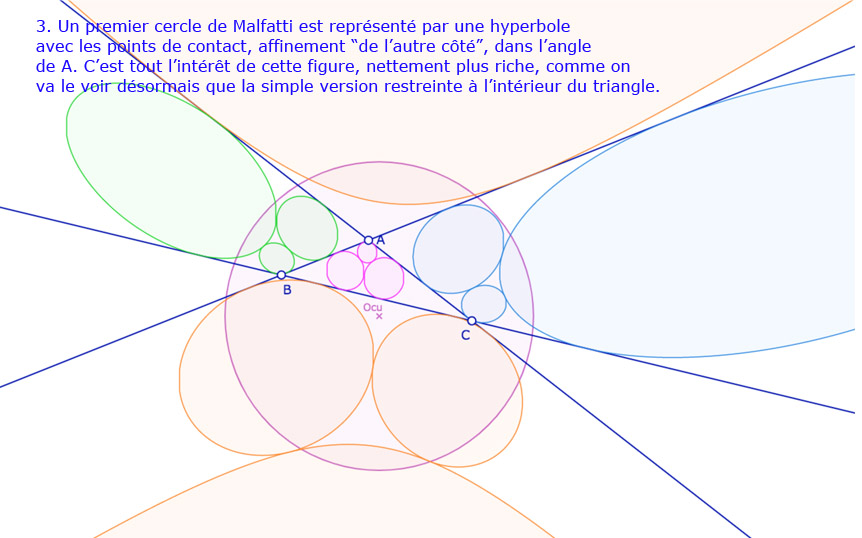
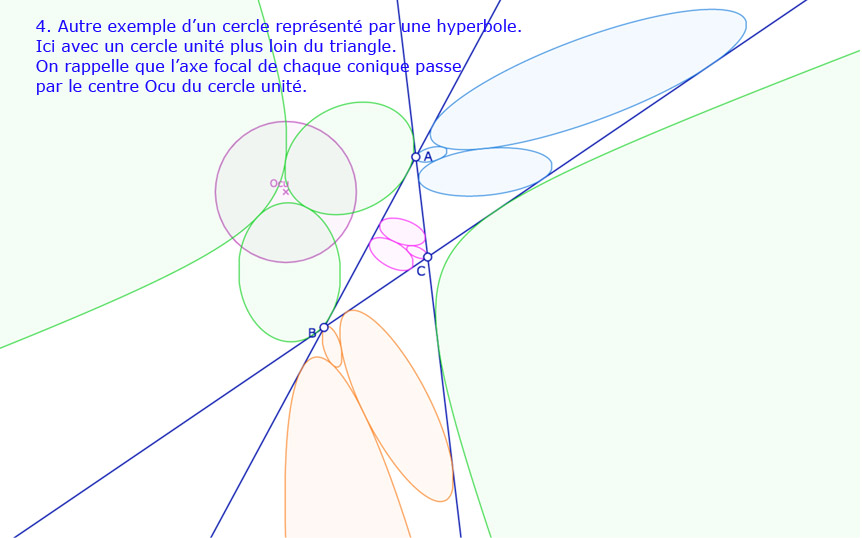
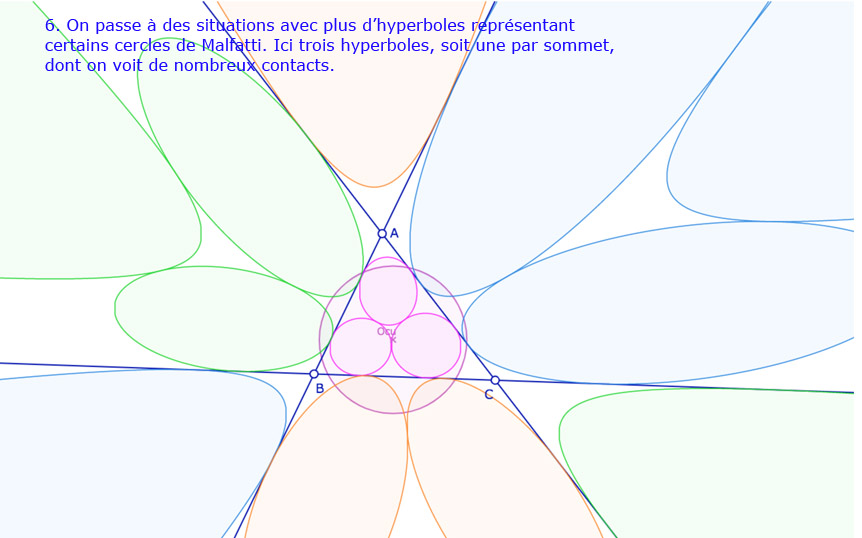
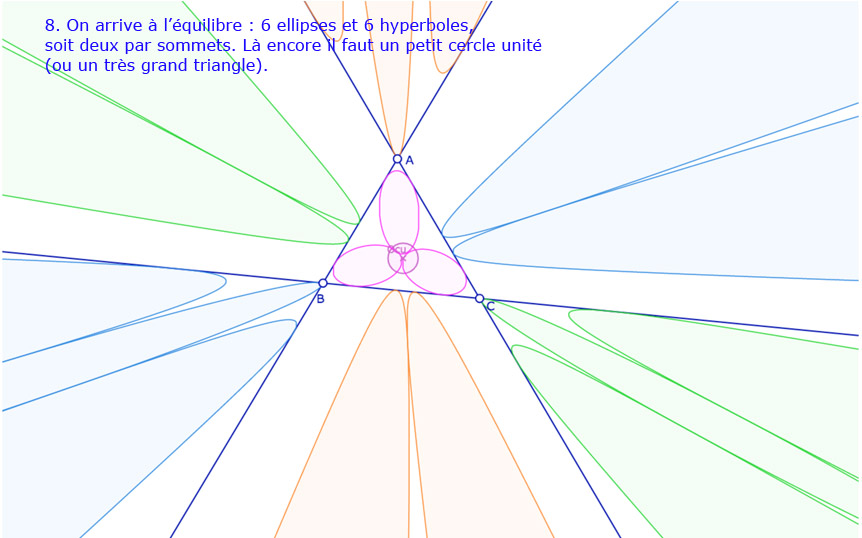
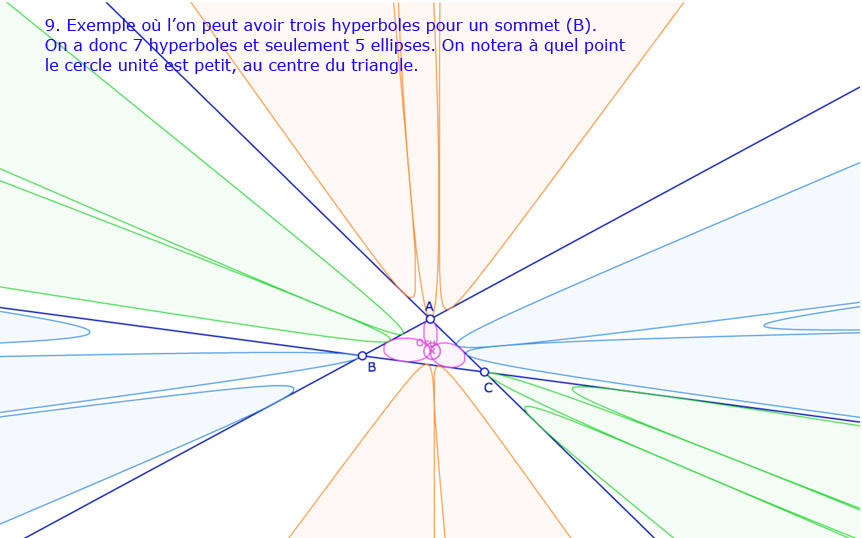
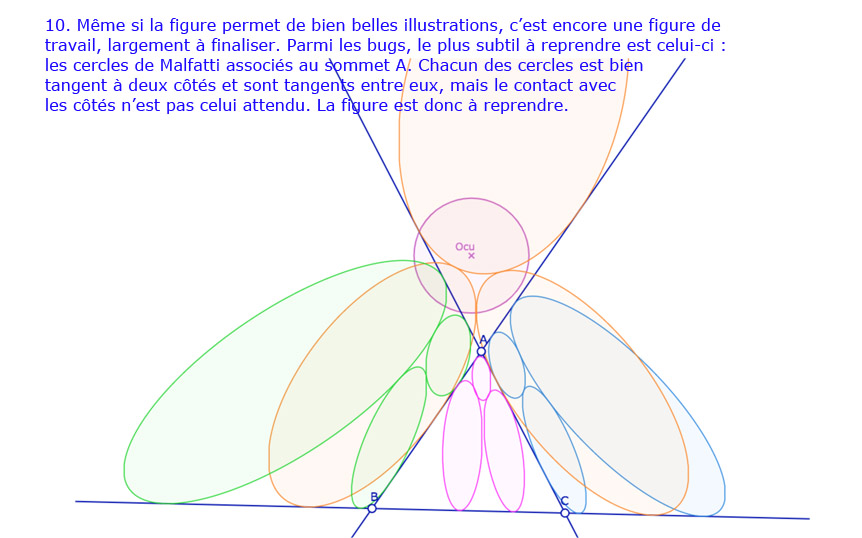
Galerie de 10 situations pour les 12 cercles de Malfatti
Comme on le dit dans la dernière illustration, il reste de nombreuses situations où la construction n’est pas correcte. En fait je pense avoir donné un peu trop de marge à un point. En voyant – un peu vite – que la dernière option n’était pas prise, je l’ai laissée.
Ouvrir cette figure de travail, temporaire, dans un nouvel onglet.
(Cette figure sera reprise ultérieurement, même s’ily a d’autres priorités pour améliorer ce site)
Dans cette figure, on agira surtout sur le centre du cercle unité \(O_{cu}\), sur le rayon du cercle, en tirant dessus, et bien entendu sur les trois points \(A, B, C\).
Construction dans KH
Comme rappelé dans les illustrations de la section précédente, pour qu’une bissectrice de deux droites existe, il faut que, soit les deux droites coupent, soit aucune ne coupent, le cercle unité. Or il y a 3 bissectrices, 6 quadrisectrices dans toutes les directions et dans la dernière étape, 3 nouvelles bissectrices (seulement car les centres de Malfatti sont sur les bissectrices de départ). Voici les droites dans un contexte classique, avec un cercle unité qui coupe toutes les droites
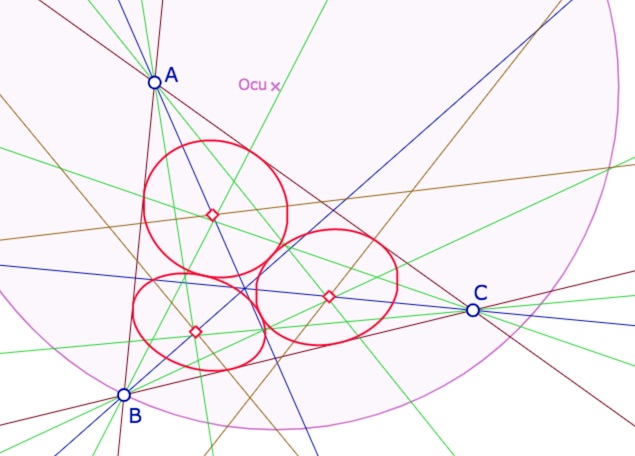
En bleu les trois bissectrices initiales, en vert les six quadrissectrices, en marron les trois dernières bissectrices.
Les limites de la situation KH
On pourrait penser qu’en diminuant le rayon du cercle unité, il y a matière à trouver une région où il n’y a pas de droites, mais en réalité, une bissectrice initiale suit toujours de près le cercle unité, et a priori il semble impossible de trouver une solution dans ce cas. En effet, on n’arrive pas a quelque chose de mieux que cela :
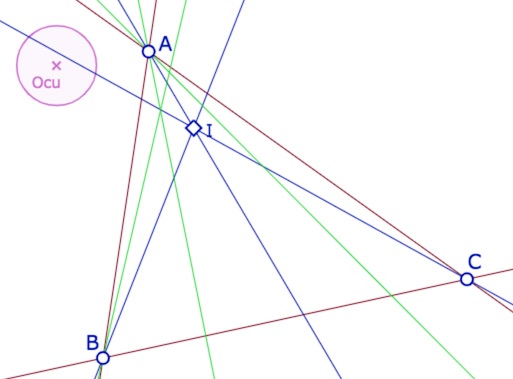
Ci-dessus, la bissectrice issue de \(C\) coupe le cercle unité. Et comme ce n’est pas le cas de la droite \((CA)\), la bissectrice de l’angle \(\widehat{ACI}\) (quadrisectrice en \(C\)) ne peut exister. Et si le cercle coupe aussi la droite \((CA)\) mais pas \((CB)\) c’est alors la bissectrice initiale qui n’existe plus.
On retrouve donc essentiellement la construction dans KB avec des point idéaux, comme déjà utilisée dans les conjugaisons sur la PS, la PSH ou la PSE, mais avec des variantes sinon originales, en tout cas plus faciles à observer, il suffit de déplacer le centre du cercle unité comme ci-dessous :
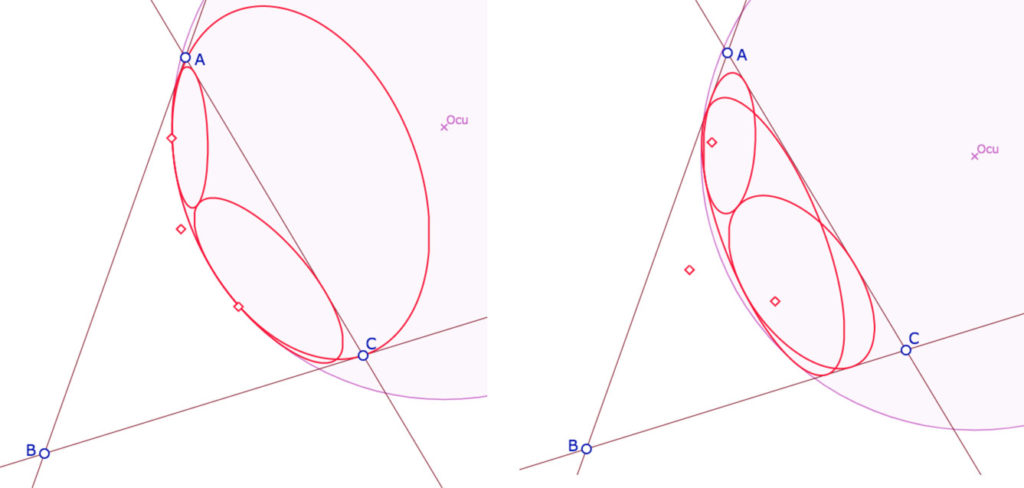
A gauche, une équidistante et (presque) deux horicycles. A droite, l’équidistante est même tritangente au triangle.
La figure de KH
Explorer la figure avec un cercle unité assez grand, puis diminuer le cercle unité
Préférer ouvrir cette figure dans un nouvel onglet
Ouvrir la figure avec les 12 bissectrices visibles dans un nouvel onglet, ce qui permet d’explorer la situation avec les droites et un petit cercle unité comme ci-dessus.
Questionnement divers
La géométrie dynamique ouvre aussi à de nouvelles questions, comme par exemple celles-ci :
Étant donné un triangle \(ABC\), peut-on construire le cercle unité pour que les 3 cycles de Malfatti soient des horicycles, au sens donné dans une section précédente ?
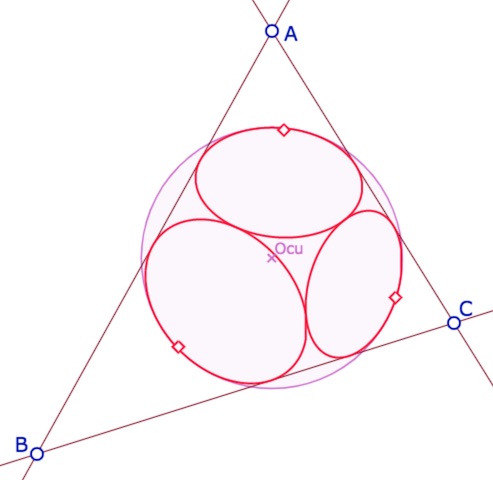
Illustration approximative de la configuration recherchée
Ou au contraire, peut-on construire trois horicycles tangents deux à deux qui soient les cercles de Malfatti d’un triangle, lui aussi à construire ? Ce second questionnement paraît nettement plus abordable. Il y a deux points de vue pour la rédaction d’un compte rendu.
• Dire tout simplement : on construit les trois horicycles deux à deux tangents et il suffit de prendre leurs tangentes communes, c’est finalement assez simple.
• Ou bien on explique aussi la gestion dynamique de la situation dont on a déjà déjà dit ailleurs qu’elle n’est pas « continue ».
On a choisi la seconde option. Les personnes non concernées par les aspects techniques iront à l’essentiel, la figure finale.
Trois horicycles tangents deux à deux
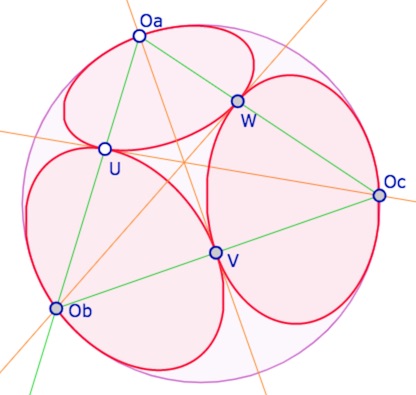
Soit un point \(O_a\) du cercle unité et un point \(U\) à l’intérieur, on construit un premier horicycle avec une macro KB car à l’intérieur du cercle unité, le modèle KH est simplement la géométrie de KB. La demi-droite \([O_aU)\) coupe le cercle unité en \(O_b\). On construit le second horicycle, naturellement tangent au premier puisque \(U\) est sur la droite des centres. Reste à construite l’horicycle tangente aux deux autres. En fait il suffit de prendre la KH-perpendiculaire à \((O_aO_b)\) passant par \(U\). Elle coupe le cercle unité en \(O_c\).
La KH-symérie orthogonale d’axe \((O_cU)\) transforme \(O_a\) en \(O_c\), l’horicycle \(H(O_a, U)\) en \(H(O_b, U)\), et l’intersection \(\{W\} = H(O_a, U) \cap [O_a O_c]\) en \(\{V\} = H(O_b,U) \cap [O_b O_c]\). Et donc l’horicycle \(H(O_c, W)\) est bien tangent aux deux autres en \(W\) et \(V\).
Construction d’un premier sommet
La première illustration de la construction KH, celle avec les droites, montre que nécessairement, le point \(A\) est sur la droite \((O_aV)\). Mais d’un autre côté si on veut que les trois horicycles soient des cycles de Malfatti d’un triangle, il suffit de construire les tangentes communes (extérieures) aux coniques prises deux à deux, et cela suffit.
Nous avons déjà fait cela, pour les envoyer sur la pseudosphère. C’est la troisième section de cette page d’applications de la conjugaison. On y montre aussi – dans une galerie d’illustrations – que si on sait construire les tangentes communes, elles s’échangent facilement entre elles. On note \(A_1, A_2, A_3\) et \(A_4\) les intersections de chacune des tangentes communes aux horicycles de centres \(O_a\) et \(O_c\) avec la droite \((O_a V)\) et on appelle ensuite \(A\) le seul de ces points qui est extérieur au cercle unité, tout en gérant aussi l’instabilité des tangentes communes intérieures car, les coniques étant tangentes, la construction par polaire réciproque peut ne pas toujours fonctionner.
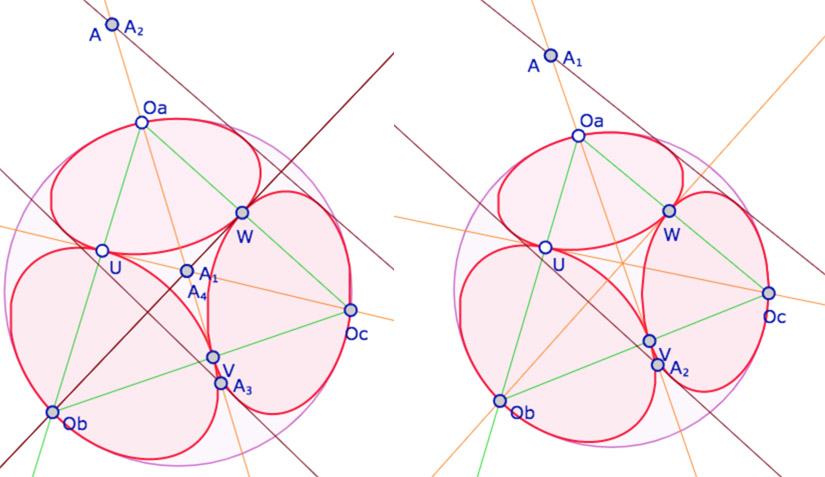
Exemple d’échanges des points \(A_i\) entre eux … à gauche les 4 tangentes existent
à droite les tangentes intérieures n’existent pas donc deux points n’existent pas.
Code utilisé ici
var result=Ocu; if (isNaN(A1.getX())==0 && d(A1,Ocu)>CU){result=A1} else {if (isNaN(A2.getX())==0 && d(A2,Ocu)>CU){result=A2} else {if (isNaN(A3.getX())==0 && d(A3,Ocu)>CU){result=A3} else {result=A4}}};result
Construction finale
On pourrait construire les autres tangentes communes, mais compte tenu de la lourdeur de la construction (la polaire réciproque) et du traitement logique final à effectuer, il est bien plus simple, à partir du point \(A\), de construire les tangentes à la première conique issues de \(A\) (construction qui n’est que du premier degré) et finaliser ainsi la figure. La construction affine de la tangente est réalisée à partir des points constituants de la conique, et il y a donc aussi, dans la manipulation dynamique, un échange possible entre les deux tangentes, comme on le voit ici avec l’inversion des points de contact \(R_a\) et \(S_a\).
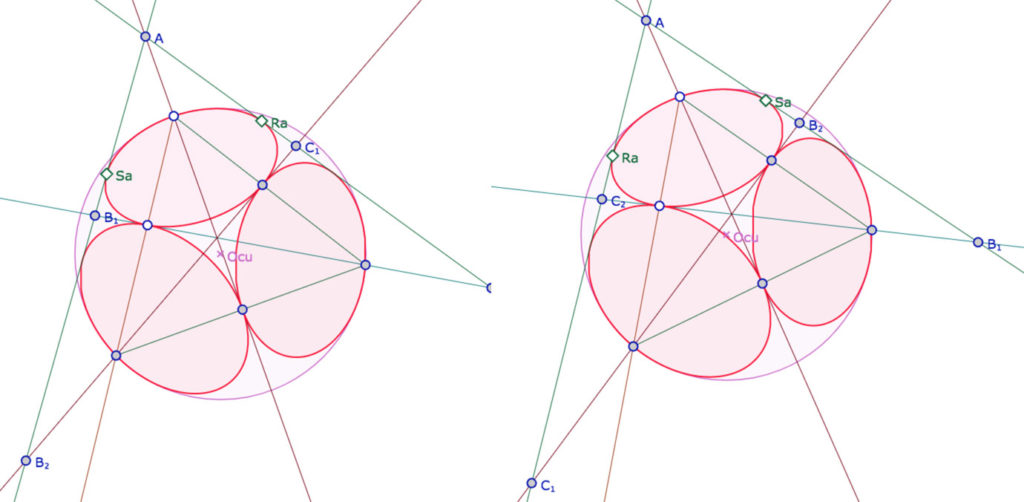
Il en résulte un nouveau traitement logique nécessaire pour définir les sommets du triangle : choix entre \(B_1\) et \(B_2\) pour \(B\) et entre \(C_1\) et \(C_2\) pour \(C\) .
Figure dynamique
Dans cette figure, on peut déplacer le centre \(O_a\) et le point de l’horicycle \(U\).
On aurait pu compléter avec un dernier traitement logique pour que \(B\) soit
toujours le point à gauche et \(C\) celui de droite.
On a ajouté le calcul de l’invariant I, présenté à l’article 3. On constate que non seulement le triangle obtenu est équilatéral mais que la longueur du côté est une constante qu’il serait intéressant de calculer.
Préférer ouvrir cette figure dans un nouvel onglet.
Reste l’autre questionnement : depuis un triangle donné, peut-on construire un cercle unité pour que les cycles de Malfatti de ce triangle soient trois horicycles ?
Liens sur les autres articles sur KE-KH
Les modèles projectifs KE et KH – 1- les droites
KEKH – 2b – Les cercles « paraboles »
KEKH – 3 – Longueur, distance et angles
KEKH – 4 – Spin d’un triangle