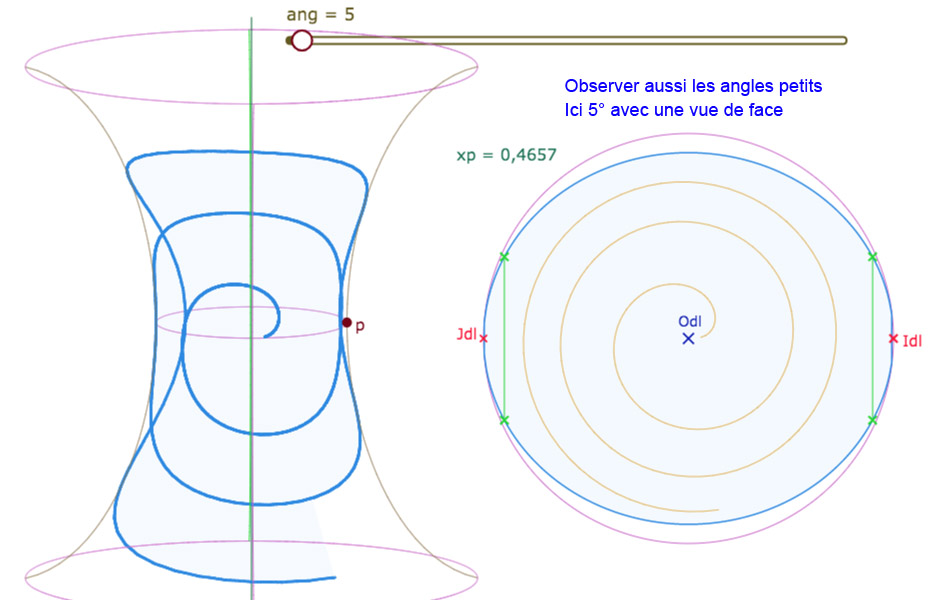
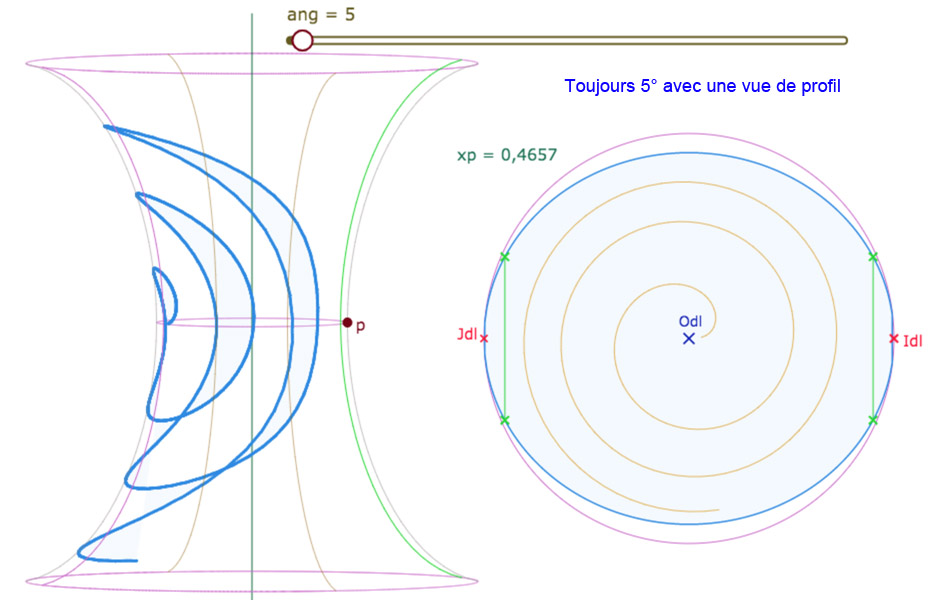
Cet article est un premier exemple d’articles plus techniques qui vont détailler les méthodes de réalisation de certaines figures. Pour faire simple, c’est le premier article dans lequel « on soulève le capot » de certaines figures. Toutefois, pour rester intéressant au plus grand nombre, on proposera aussi quelques « divertissements » sur ces techniques certes un peu éloignés d’un intérêt mathématique mais toujours visuellement parlant.
Dans cet article nous présentant deux façons de programmer le remplissage des polygones sur la pseudosphère et la pseudosphère hyperbolique : une programmation en Blockly et une programmation directement en JavaScript. La première est un peu plus longue, mais facile d’accès, et sûre (pas d’erreur de syntaxe). La seconde est plus concise, mais peut-être un peu plus ésotérique. Elle a surtout l’intérêt de pouvoir être transformée en macro-construction. C’est aussi surtout l’occasion de parler de l’utilisation de l’outil expression (icone calculatrice).
L’outil « liste de segments »
On peut créer une liste de segment par un clic long sur la page de DGPad (menu de l’illustration de gauche), mais aussi simplement en créant une liste – un seul point suffit – et en la transformant ensuite par programmation.
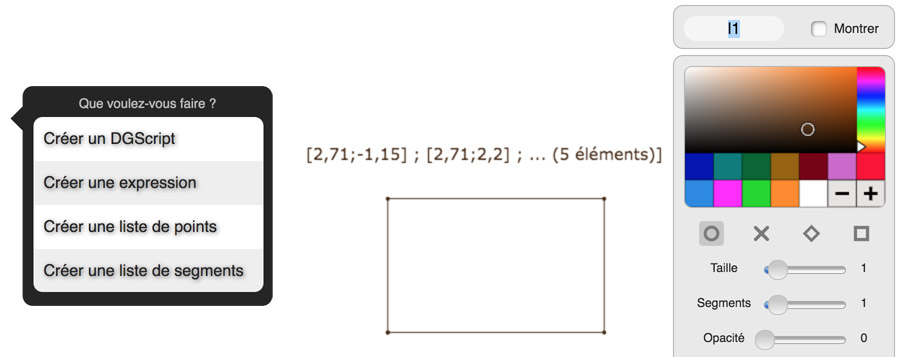
Quand on crée une liste de segments, le logiciel crée, par défaut, une expression sur la forme d’une liste de 5 points (ci-dessus au gauche dont on ne voit qu’un extrait) et affiche la représentation graphique de cette expression qui a le statut interne de List, ci-dessus, le tracé du rectangle, dont le nom – dans l’inspecteur d’objets – est l1.
Si on part d’une simple expression (d’une liste) de points , il n’y a pas de tracé graphique par défaut. On fait apparaître le tracé en cliquant sur l’icone segment (ci-dessous). Dans les deux cas l’expression et sa représentation graphique (List) existent toutes les deux, et ont des réglages spécifiques.

Dans la suite on se propose d’utiliser les listes de segments pour remplir – par opacité – les polygones construits sur les deux surfaces pseudosphériques étudiées dans ce site.
Pourquoi les listes de segments ?
Et en particulier pourquoi pas tout simplement le lieu de l’image d’un point sur polygone ? En effet, on a vu, par exemple sur la page traitant des cercles sur la pseudosphère, que le cercle-lieu peut être rempli par opacité. Or on peut prendre un point sur polygone et construire le lieu de son image. Mais il semble que le type soit prédominant : le lieu image d’un polygone se comporte comme un polygone (côtés affines) donc inutilisable ici.
Mais surtout, l’usage des listes de segments a un avantage, intrinsèque à l’objet, déterminant : les extrémités des segments, même s’ils sont accessibles à l’inspecteur d’objets comme des points, ne sont pas des points construits. Il en résulte une plus grande fluidité de cet objet bien spécifique car si la représentation graphique (la liste associée à l’expression) est dessinée, dynamiquement bien entendu, elle n’est pas composée d’objets construits comme dans d’autres logiciels. Cette fluidité et le remplissage par l’opacité sont les deux raisons de ce choix.
Diviser les KB-segments en 20
dans le passage à la pseudosphère.
Le principe retenu est de partir de segments du disque limite de Beltrami (modèle KB) et de construire des listes de segments à partir des images sur la surface pseudosphérique des extrémités des segments de KB. On choisit de recouvrir le segment image – qui est toujours un lieu – par une liste de 20 segments, ce qui suffit pour le remplissage. Voyons ce qu’il en est sur l’exemple du remplissage du polygone étoilé associé au pentagone orthogonal comme on l’a déjà présenté à la fin de cet article.
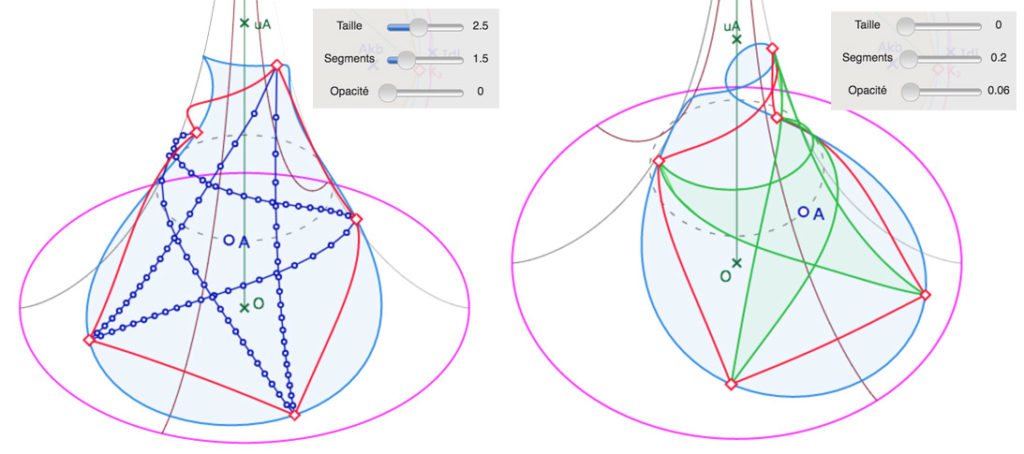
à gauche : la représentation graphique de la liste de segments, avec le réglage associé : gros points et segments épais.
à droite : on a remis les côtés du polygone étoilés (lieux verts) et on rempli le polygone par opacité en cachant les points et en minimisant les segments, cachés par les segments lieux (on ne peut pas mettre les deux réglages à 0).
On retient que les côtés sont tracés par les lieux et le remplissage par les listes de segments, en pratique cachés par les segments-lieux.
Rappel des calculs du passage de KB à PS
Les coordonnées \((x, y)\) sont rapportées à l’origine \(Odl\). On a alors déjà vu que la longitude est donnée par \(\displaystyle \theta=\frac{y}{x-1}\) et la latitude \(u=ch^{-1}\displaystyle \left(\frac{\sqrt{1-x^2-y^2}}{1-x}\right)\) (car \(x<1\)).
Par ailleurs \(ch^{-1}(u)=ln(u+\sqrt{u^2-1})\).
Et le point de la pseudosphère a pour coordonnées \(\displaystyle \left( \frac{1}{ch \; u}cos \theta, \; \frac{1}{ch \; u}sin \theta, \; u -th \; u \right)\).
La construction de la liste
de segments par Blockly
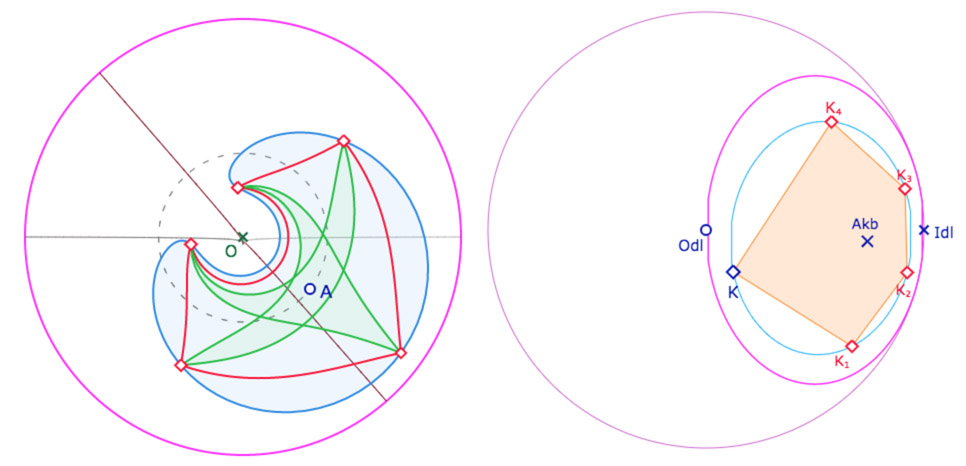
à gauche : vue de dessus du pentagone orthogonal rt
à droite : pour les noms des sommets du pentagone dans KB (pour le programme suivant)
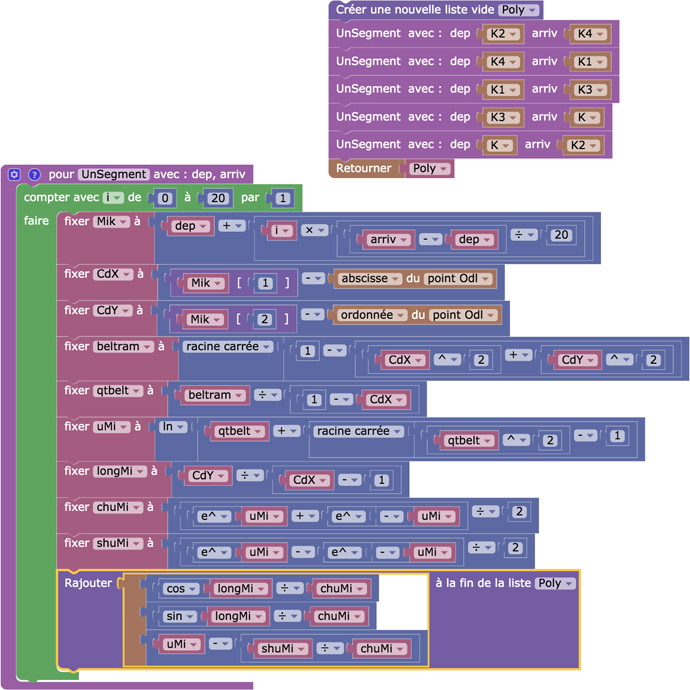
Ce code est associé à une expression qui prend, au final, la valeur de l’expression Poly construite par le programme. L’essentiel du code est dans une procédure qui construit la liste de segments sur l’image d’un segment. On commence par la définition des 21 points intermédiaires \(M_{ik}\) (k car encore dans KB). La seule chose à noter dans cette procédure est que, dans DGPad, la première coordonnée d’un point \(M\) est \(M[0]\) – qui s’écrit aussi \(x(M)\) mais seulement « dans DGPad » – et la seconde \(M[1]\) (mais aussi \(y(M)\) dans DGPad), alors que, dans Blockly, la première coordonnée est \(M[1]\) et la seconde \(M[2]\), d’où les écritures – un peu surprenantes – de \(CdX\) et \(CdY\) qui mélangent les deux. Ensuite \(uM_i\) est l’ordonnée du point en cours sur la PS et \(LongM_i\) est sa longitude. Cette procédure UnSegment est réutilisable dans toute figure. On peut facilement la copier. Seul le programme principal est à adapter en fonction du contexte.
Attention : la figure étant placée dans l’iframe en mode restriction, on ne peut pas animer le point \(M\), mais on peut le déplacer. On peut aussi agir sur le point \(A\) ou la latitude \(u_A\). Penser à tourner la pseudosphère.
Pour lancer une animation sur M et surtout voir le code Blockly, utiliser cette autre figure. Pour le code Blockly cliquer sur l’une des deux listes PentaOrtho ou PentaEtoile en bas de la figure. Il faut être en mode standard, flèche à gauche activée, et choisir l’icone Blockly, la dernière à droite, en ayant cliqué sur une liste, comme ceci. :
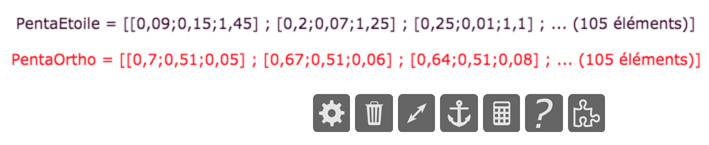
Avant d’aborder l’écriture équivalente en JavaScript – on le fera sur la PSH – commençons par une présentation de l’outil « expression-programme », dans des cas euclidiens élémentaires.
Présentation générale de l’utilisation du JavaScript dans une expression-programme
Règles des « expressions-programme »
1. Le dernier point virgule est une séparation :
• ce qu’il y a avant est du JavaScript « pur », avec quelques simplifications (pas de Math.cos mais juste cos par exemple, de même pour π au lieu de Math.PI etc – utilisation des fonctions du clavier math de DGPad.
• la liste créée en interne est renvoyée à DGPad par la variable placée après le dernier point-virgule.
2. Il en résulte qu’il n’y a pas d’extension géométrique du JavaScript (pas de Point, Line Circle, etc)
3. On ne peut pas écrire la construction d’un point directement comme le point \(M_{ik}\) dans le code Blockly ci-dessus. Il faut passer par leurs coordonnées (sera plus clair sur les exemples).
Exemple 1 – Tournesol dynamique
Une modélisation du cœur du tournesol, proposée, entre autre, par Aristid Lindenmayer dans « The Algorithmic Beauty of Plants » (Springer p. 100) est basée sur les points \(P_k\) d’affixes \(C \sqrt{k} e^{ik\theta}\) où \(\theta\) est lié au nombre d’or \(\Phi\) par \(\displaystyle \theta=\frac{2\pi}{1+\Phi}\) soit environ 137,5°.
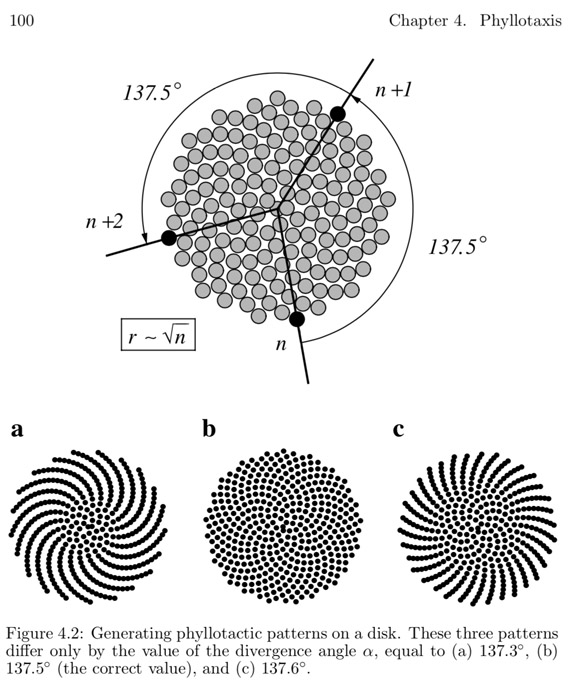
On se propose de mettre en œuvre cette modélisation par une liste de points, en ajoutant un curseur d’angle (nommé ang ci-dessous) à la place de la valeur fixe de 137,5°. Le code est alors simplement le suivant (copie d’écran)

Dont voici la figure associée
a – Commencer par agir sur le curseur (incrément réglé à 0,5°).
b – Sélectionner l’inspecteur d’objet (icone roue), cliquer la représentation graphique (ci-dessous au centre), puis modifier l’aspect en mettant les points à 0 et les segments à 0.4. Enlever l’opacité (ci-dessous à droite).
On passe ainsi, avec la même expression E1, d’une liste de points à une liste de segments et réciproquement.
c – Pour retrouver la figure initiale, relancer la figure avec la première icone en haut de l’iframe.

Dans ce premier exemple, on ne voit pas l’obligation d’utiliser les points par leurs coordonnées car le point que l’on construit l’est fait naturellement de cette façon. Voici un second exemple où c’est nettement plus parlant.
Exemple 2 – Sierpiński
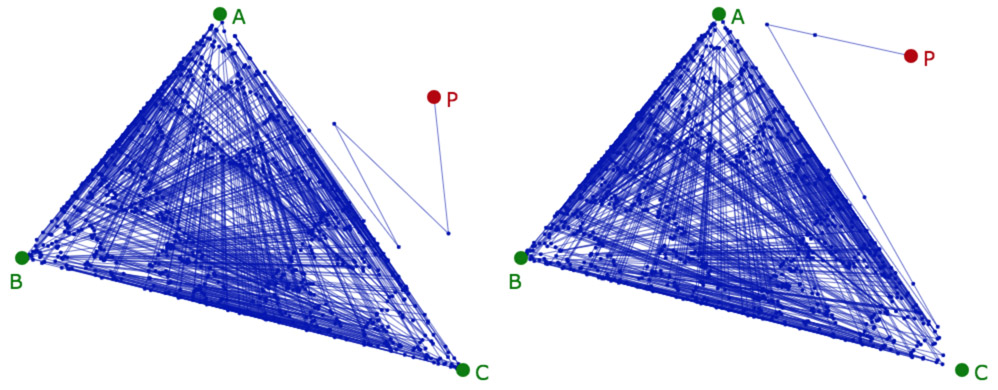
On construit le nuage de Sierpiński d’un triangle \(ABC\) par approche probabiliste depuis un point \(P\). L’algorithme est très classique. On se donne une variable ch qui prend aléatoirement les valeurs 0, 1 ou 2, ce qui permet de sélectionner le « sommet suivant » A, B ou C pour prendre le milieu du point courant et du point suivant. On a surtout choisi cet algorithme pour montrer qu’il faut utiliser ou définir les points par leurs coordonnées comme \(A[0]\) et \(A[1]\), alors que ce serait plus simple en Blockly.

a – Déplacer les points \(P, A, B\), ou \(C\).
b – Transformer, comme dans l’exemple précédent, la liste de points en liste de segments. Cela permet de mieux voir le début du trajet et même lire les premières valeurs de ch, comme illustré ci-dessous
Exemple 3 – Rupture d’une liste de segments
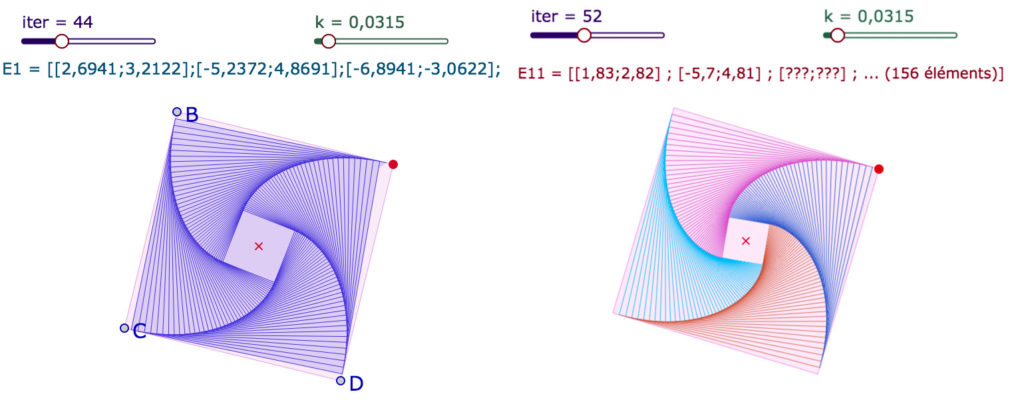
Avec les listes de segments, on peut avoir besoin de couper une liste pour que les segments ne s’enchainent pas systématiquement. Voici un exemple, là encore archétypique : on part d’une courbe de poursuite sur 4 sommets d’un carré, et on se propose de séparer la liste en 4 pour y mettre 4 couleurs différentes. Pour cela il suffit de prendre un extrait de la liste principale, exactement comme une suite extraite, et ajouter un point de coordonnées [NaN, NaN].
L’intérêt – et même le principal intérêt – d’utiliser des expressions-programme (au lieu de Blockly) pour construire des listes de segments est qu’on peut les placer dans des macro-constructions, et faire tout simplement des figures comme celle-ci.
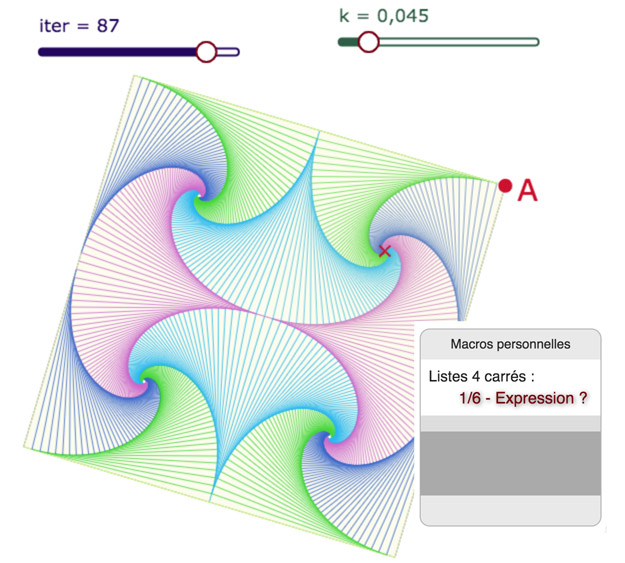
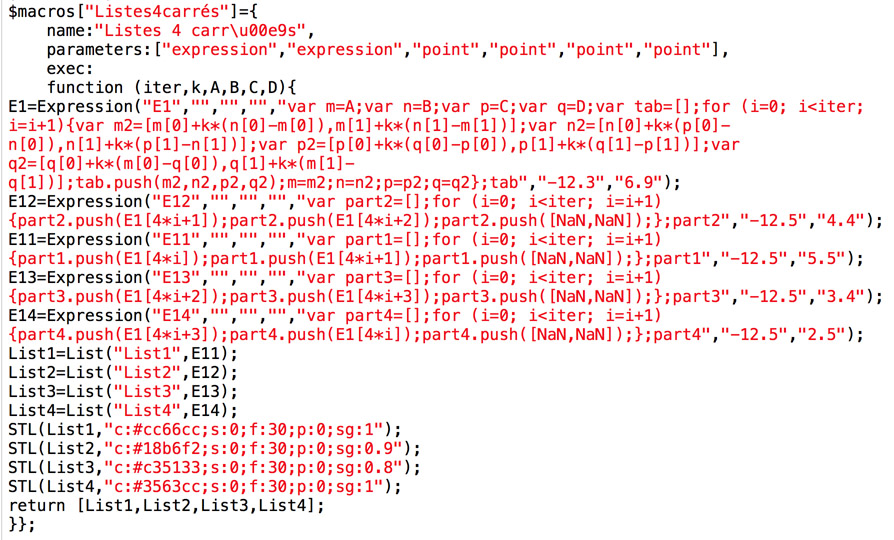
Voici le code de la macro, qui reprend la principale expression-programme et en déduit les 4 expressions extraites. C’est l’occasion de bien voir la différence entre l’expression E11 et la liste associée List1 à l’expression. Le code STL est celui du style, qui donne en particulier la couleur. C’est géré automatiquement quand on fait la macro. On remarquera que la macro ne renvoie que les 4 listes extraites (l’aspect graphique) mais aucune des 5 expressions nécessaires à cette production graphique. Ayant fait la figure du premier carré, transformée en macro, on applique cette macro à trois autres carrés pour produire la figure de l’illustration.
Lancer cette figure (finalisée) dans un nouvel onglet.
Préférer terminer la figure par l’application de la macro précédente. Il faut d’abord montrer les curseurs iter et k, Commencer par l’appliquer aux points \(A, B, C, D\). Ensuite – c’est l’intérêt de cette figure – réfléchir à l’ordre des points d’application pour qu’il y ait continuité des couleurs.
Pour annuler une application erronée de la macro (cela arrive !), il suffit de cliquer sur le bouton retour en bas à droite de l’écran : cela supprime tout ce que l’on vient de faire, y compris ce qui n’apparaît pas à l’écran.
Ensuite, on peut s’amuser à toutes sortes de variantes, comme celle-ci.
Lancer cette figure dans un nouvel onglet.
Application au remplissage de polygones sur la PSH
Comme dans le cas de PS, on part des segments d’un polygone dans KB. On part d’un point \(M_{kb}\) dans le disque limite KB, On rappelle que l’abscisse \(x_{M_{kb}}\) détermine la longitude du point sur la PSH par \(\theta_{M_{PSH}} = \displaystyle \frac{1}{p}th^{-1}(x_{M_{kb}})\) et son ordonnée \(y_{M_{kb}}\) permet d’écrire \(u_{M_{PSH}} =th^{-1} \left(y_{M_{kb}}ch(p \theta_{M_{PSH}})\right)\). Ensuite le point \(M_{PSH}\) a pour coordonnées \(\displaystyle \left( p \, ch (u_{M_{PSH}}) \, cos(\theta_{M_{PSH}}), \, p \, ch(u_{M_{PSH}}) \, sin(\theta_{M_{PSH}}), \, g(u_{M_{PSH}})\right)\) où \(g\) est l’approximation de la génératrice et \(p\) le paramètre de la surface.
Juste pour le fun on va utiliser un curseur pour faire tourner, sur les 5 côtés d’un pentagone orthogonal, une liste segment qui va recouvrir le côté désigné par le curseur. Ce curseur s’appelle curs, et les sommets du pentagone dans KB sont placés dans la liste LesPts. Dans le code suivant, le paramètre \(p\) se note \(xp\) et la longitude est décalée de \(\pi\) pour que la feuille principale soit sur l’intervalle \(]-\pi, \pi]\). Ce qui s’écrit :
var dep=LesPts[curs];var arr=LesPts[curs+1]; var nmax=20;var tab=[];for (var i=0;i<=nmax;i++){var Mikb=[dep[0]+i(arr[0]-dep[0])/nmax,dep[1]+i(arr[1]-dep[1])/nmax];var longMik=log((1+Mikb[0]-Odl[0])/(1-Mikb[0]+Odl[0]))/(2xp);var uMik=log((1+(Mikb[1]-Odl[1])(exp(xplongMik)+exp(-xplongMik))/2)/(1-(Mikb[1]-Odl[1])(exp(xplongMik)+exp(-xplongMik))/2))/2;var Mik=[xp(exp(uMik)+exp(-uMik))cos(longMik-π)/2,xp(exp(uMik)+exp(-uMik))*sin(longMik-π)/2,g(uMik)];tab.push(Mik);};tab
Figure associée
Agir sur le curseur curs pour voir tourner la liste de segments. Modifier également le point \(K\).
Transformation en macro pour remplir des pentagones
Il suffit de répéter 5 fois ce qui précède et le placer dans une macro. Pour la démonstration de son utilisation, on aurait pu faire une macro minimaliste, mais on a voulu présenter ici quelque chose de plus réaliste en terme d’optimisation, c’est la raison pour laquelle cette macro est une « vrai macro », comme celles utilisées dans ce site.
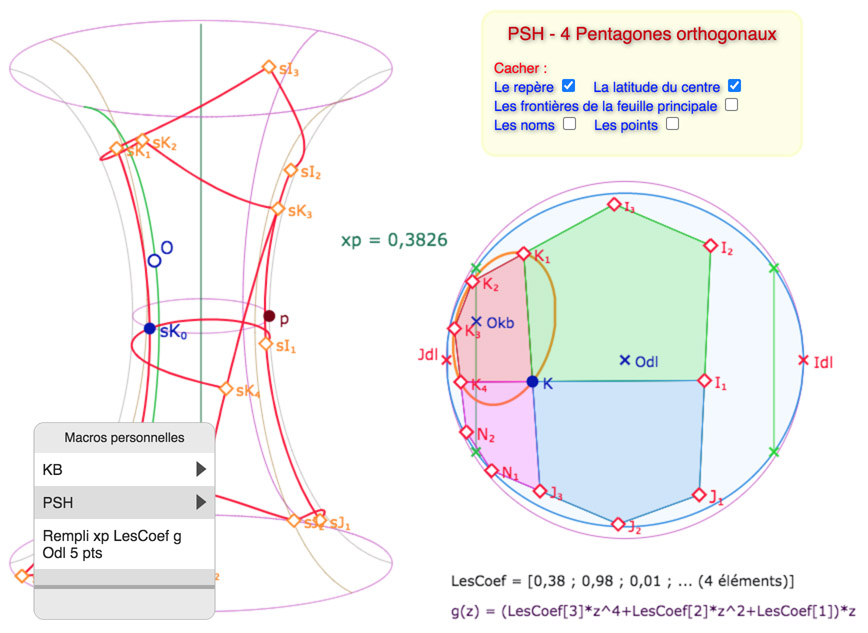
Cette macro (Rempli …) demande en effet, avant les 5 points d’un pentagone de KB, les 3 expressions \(xp\), \(LesCoef\), et \(g\), puis le point \(Odl\) et ensuite \(K, K_1, K_2, K_3, K_4\) pour le pentagone rouge. Une version simplifiée aurait pu enlever les deux expressions \(LesCoef\), et \(g\), mais elles seraient reconstruites, avec un autre nom et utilisées à la place des expressions originales. Cela complexifie inutilement la figure. surtout dans des figures déjà assez complexes.
Vous pouvez utiliser cette macro dans cette figure (s’ouvre dans un nouvel onglet), et l’appliquer aux 4 pentagones orthogonaux autour de \(K\). Le remplissage est déjà travaillé – on ne voit pas les points comme à la figure précédente – mais il sera toujours rouge. Il faut le sélectionner pour en changer la couleur. Pour cela il sera peut-être nécessaire de cacher un côté du pentagone sur la PSH pour « attraper » le remplissage, et non pas le segment. Cela dépend du contexte de la figure et de l’habitude à utiliser le logiciel.
Rappel sur l’utilisation de cette figure : éviter de déplacer le point \(O\), bien optimisé, mais par contre on peut déplacer (un peu) sa latitude \(u_O\) – la rendre visible – et bien entendu le point \(K\). Être en mode consultation pour cela (aucun outil du tableau de bord sélectionné).
… et divertissements associés
On se propose de terminer cet article par deux applications certes, peu mathématique, mais qui illustre l’efficacité de la notion d’expression-programmes. Nous allons plaquer les deux exercices d’appropriation de ces expressions-programme – tournesol dynamique et carré de poursuite – sur la surface de la PSH.
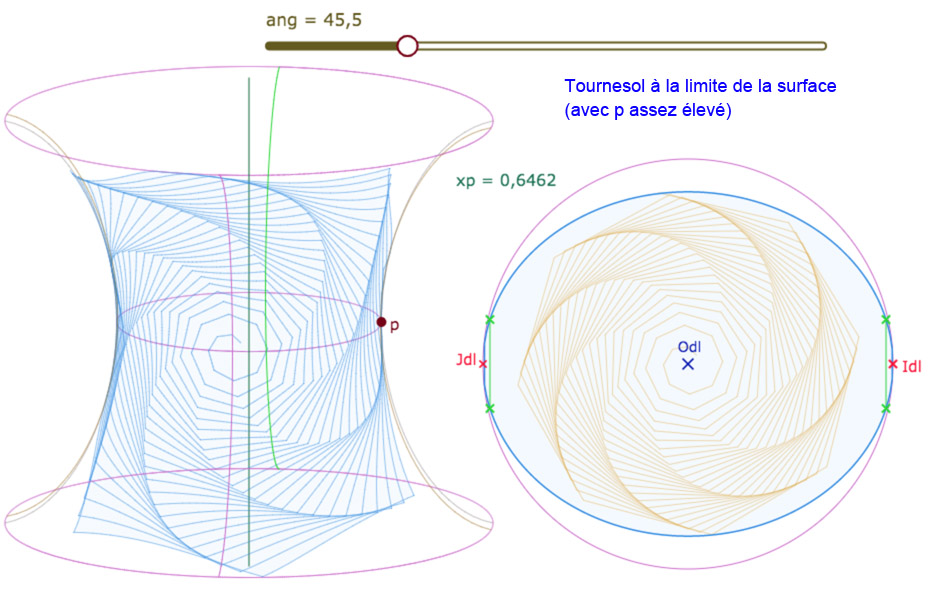
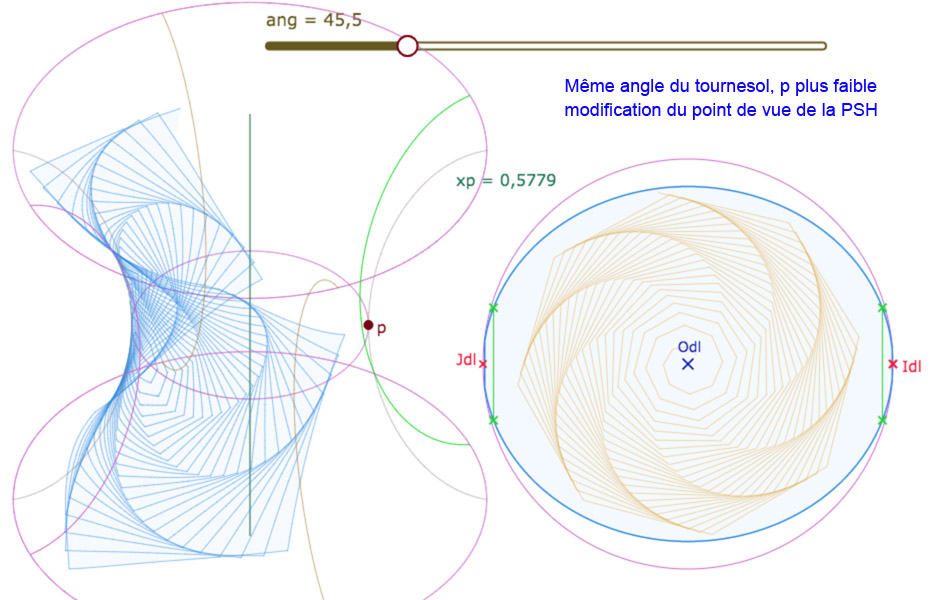
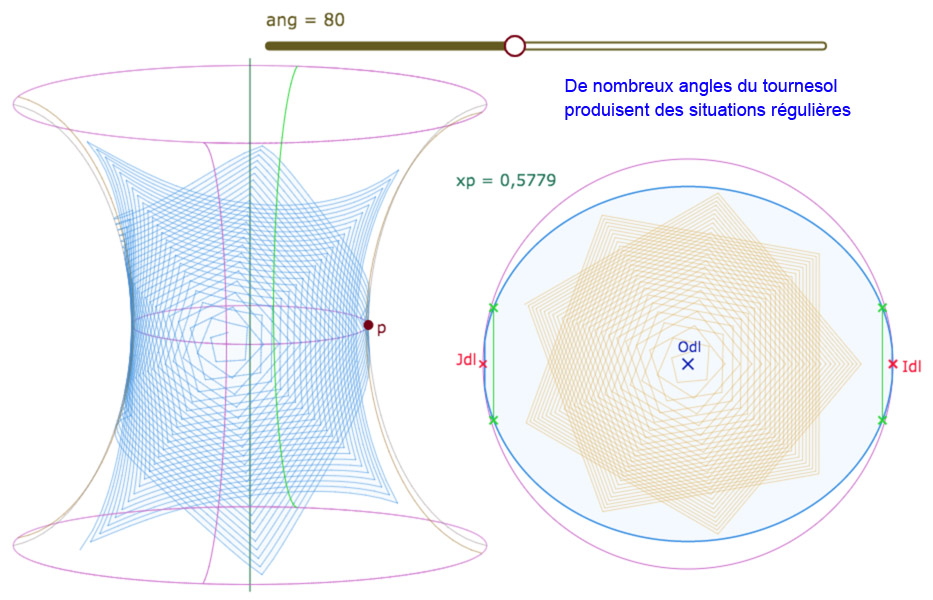
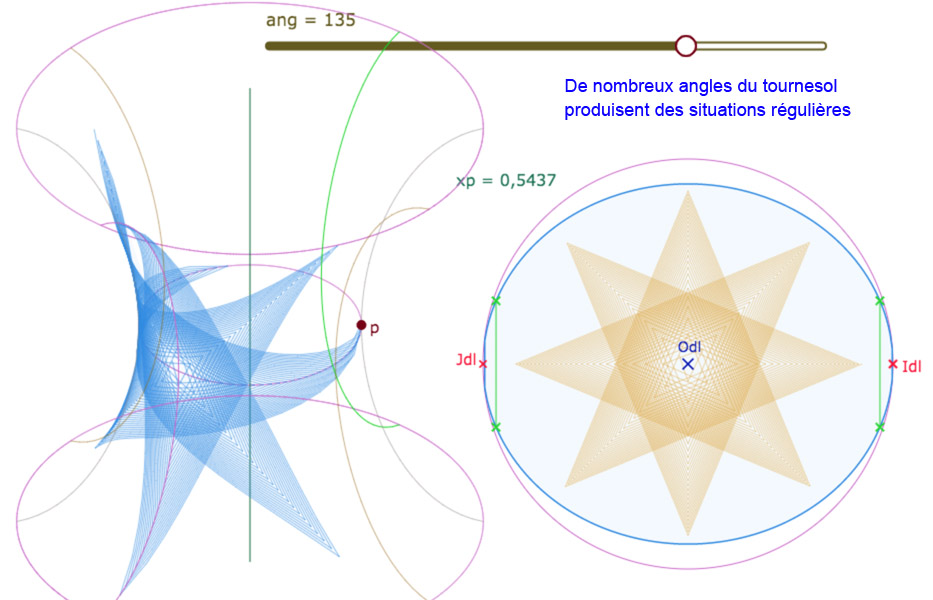
Tournesol sur la PSH
En réalité, l’activité n’est pas vraiment mathématique en ce sens que l’angle euclidien constant utilisé ne correspond pas à un angle hyperbolique constant. Et pourtant, une certaine régularité est reproduite, en particulier pour des angles spécifiques (diviseurs de 360 en particulier). Voici le code utilisé pour cette figure
var tab=[];for (var i=1;i<=200;i++){var u1=0.06sqrt(i); var k1=iangπ/180; var v1=[Odl[0]+u1cos(k1),Odl[1]+u1sin(k1)];var u2=0.06sqrt(i+1); var k2=(i+1)angπ/180; var v2=[Odl[0]+u2cos(k2),Odl[1]+u2sin(k2)]; for (var ug=0;ug<=20;ug++){var vk=[v1[0]+ug(v2[0]-v1[0])/20,v1[1]+ug(v2[1]-v1[1])/20];var longMv=log((1+vk[0]-Odl[0])/(1-vk[0]+Odl[0]))/(2xp);var uMv=log((1+(vk[1]-Odl[1])(exp(xplongMv)+exp(-xplongMv))/2)/(1-(vk[1]-Odl[1])(exp(xplongMv)+exp(-xplongMv))/2))/2;var Mv=[xp(exp(uMv)+exp(-uMv))cos(longMv-π)/2,xp(exp(uMv)+exp(-uMv))*sin(longMv-π)/2,g(uMv)];tab.push(Mv);};};tab
Ce qui donne une liste finale assez conséquente, conjuguée en deux versions selon l’étendue de la boucle interne de la variable \(ug\).

Galerie de 6 illustrations de la figure suivante
Lancer la figure dans la version standard max20 ou dans la version max25.
Carré de poursuite sur la PSH
Dans KB, le carré étant centré au centre du cercle, qui est le seul point où les angles sont conformes, le carré euclidien initial dans KB est bien un KB-carré, mais bien entendu avec un angle au sommet qui n’est pas de 90°
Là encore, les listes en jeu pour la PSH sont assez lourdes, comme on le voit dans cette illustration
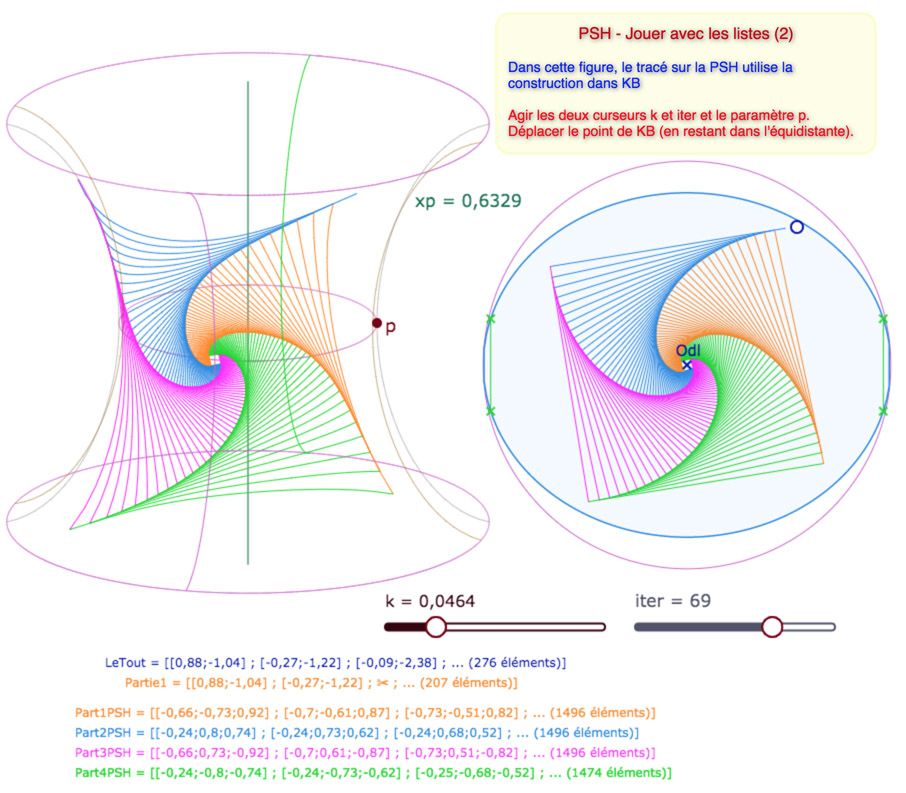
Le code dans KB est réalisé en Blockly, celui sur la PSH en JavaScript
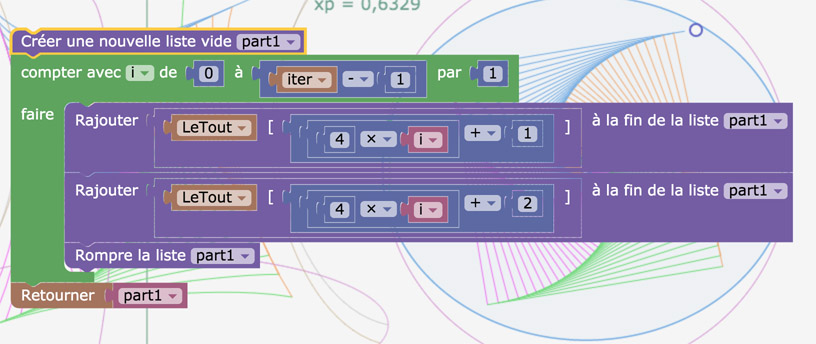
Et le code sur la PSH, désormais très classique maintenant …
var tab=[];for (var i=0;i<(iter-1);i++){ var v1=Partie1[3i]; var v2=Partie1[3i+1]; for (var ug=0;ug<=20;ug++){var vk=[v1[0]+ug(v2[0]-v1[0])/20,v1[1]+ug(v2[1]-v1[1])/20];var longMv=log((1+vk[0]-Odl[0])/(1-vk[0]+Odl[0]))/(2xp);var uMv=log((1+(vk[1]-Odl[1])(exp(xplongMv)+exp(-xplongMv))/2)/(1-(vk[1]-Odl[1])(exp(xplongMv)+exp(-xplongMv))/2))/2;var Mv=[xp(exp(uMv)+exp(-uMv))cos(longMv-π)/2,xp(exp(uMv)+exp(-uMv))*sin(longMv-π)/2,g(uMv)];tab.push(Mv);};tab.push([NaN,NaN,NaN]);};tab
Lancer la figure CourbePoursuite sur PSH dans un nouvel onglet.