On se propose de montrer – de manière absolue, c’est-à-dire pour les géométries hyperbolique, euclidienne et elliptique – une propriété des milieux des sommets d’un triangle vis à vis des points de contact du cercle inscrit et des cycles exinscrits avec les droites du triangle, dont voici une illustration hyperbolique.
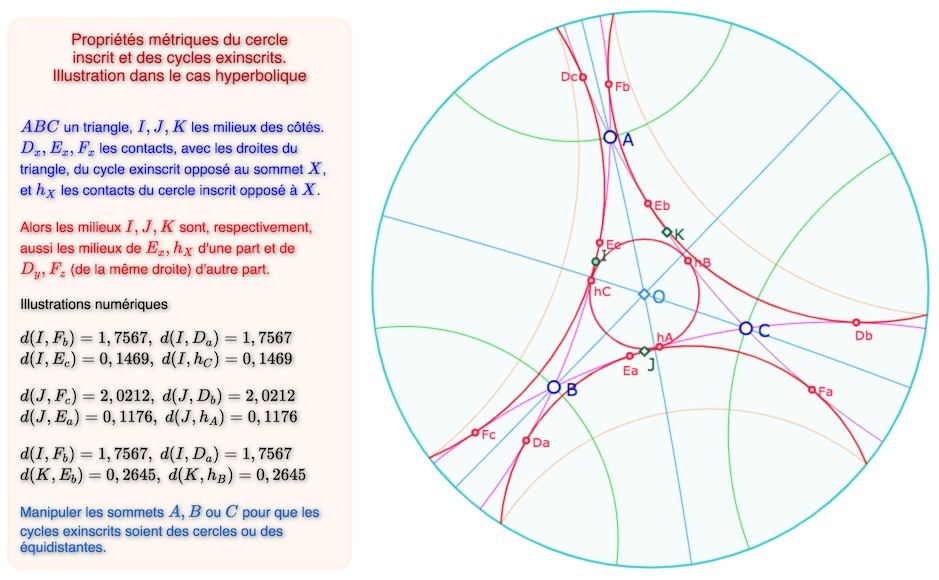
On notera que les points de contact \(D_x, E_x, F_x\) sont construits indépendamment du type de cycle (cercle ou équidistante) par une conséquence du Th21b de cette page.
Ouvrir cette figure dans un nouvel onglet.
Lecture absolue de la projection
orthogonale d’un milieu – Application
On sait que la projection orthogonale d’un milieu est le milieu des projetés seulement dans le cas de la géométrie euclidienne. Commençons par reprendre (rapidement) l’argumentaire euclidien dans le contexte qui nous intéresse :
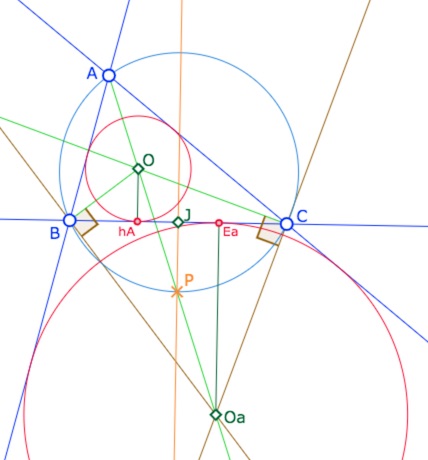
Ci-contre \(O\) est le centre du cercle inscrit de \(ABC\), \(O_a\) le centre du cercle exinscrit opposé au sommet \(A\). Dans le cas euclidien, on montre que le milieu \(J\) de \(B\) et \(C\) est aussi le milieu des contacts \(h_A\) et \(E_a\) du cercle inscrit et du cercle exinscrit avec \((BC)\) généralement avec deux propriétés spécifiquement euclidiennes : la cocyclicité et le conservation du milieu par projection orthogonale. En effet, en appelant \(P\) l’intersection de la bissectrice \([OO_a]\) et du cercle circonscrit à \(ABC\), par des considérations d’angles, on voit qu’il est aussi sur la médiatrice de \([BC]\). Par ailleurs les points \(O, B, O_a, C\) sont cocycliques sur le cercle de diamètre \(OO_a\). Son centre est à la fois sur la bissectrice et la médiatrice. C’est donc le point \(P\) (sauf si le triangle est isocèle en \(A\) car la médiatrice et la bissectrice sont confondues, mais on arrive au même résultat par un autre argument). Il en résulte le milieu \(J\) de \([BC]\), comme projeté orthogonal de \(P\), est aussi le milieu de \(h_A\) et \(E_a\) comme projetés orthogonaux de \(O\) et \(O_a\).
Mias les deux principaux arguments sont uniquement euclidiens. Pour obtenir un théorème absolu, il faut un regard différent sur la situation. Pour cela, on va essentiellement utiliser le théorème de Hjelmslev. En effet, on dispose de deux pinceaux \(\mathscr{P}_{(OB)(OC)}\) et \(\mathscr{P}_{(O_aB)(O_aC)}\) avec les angles droits en \(B\) et \(C\), et la droite \((OO_a)\) qui appartient aux deux pinceaux. Or le théorème de Hjelmslev dit que la droite \((OO_a)\) appartient aux deux pinceaux (quand on sait qu’elle appartient à l’un deux) si le produit des trois droites \((OB), (OO_a), (OC)\) est orthogonal à \((BC)\). Donc ce produit est la droite \((Oh_A)\). De même le produit des droites \((O_aB), (O_aO), (O_aC)\) va être la droite \((O_aE_a)\).
Une version absolue de la propriété des milieux
Par ailleurs, on n’a pas besoin que les pinceaux soient à centre comme dans le cas euclidien (même si on sait que c’est le cas des bissectrices « intérieures » au triangle). Voyons donc une configuration un peu plus générale, par application du théorème de Hjelmselv.
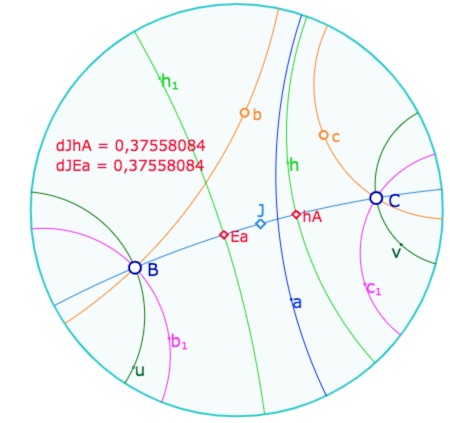
Une version absolue du résultat précédent : le milieu de \(B\) et \(C\) est aussi milieu
des intersections de \((BC)\) avec les produits \(bac\) et \(b_1ac_1\) qui sont les
perpendiculaires à \((BC)\) issues des deux pinceaux \(\mathscr{P}_{bc}\) et \(\mathscr{P}_{b_1c_1}\).
Dans la figure ci-dessus, on se donne deux points \(B\) et \(C\) définissant chacun les droites \((Bb)\) et \(Cc)\), les points \(b, \,c\) servant de poignées pour les droites du même nom. Par \(B\) et \(C\) on construit les perpendiculaires \(b_1\) et \(c_1\). On a donc \(B=bb_1=b_1b\) et \(C=cc_1=c_1c\). On se place dans la situation où les deux pinceaux \(\mathscr{P}_{bc}\) et \(\mathscr{P}_{b_1c_1}\) ont une droite commune, la droite \(a\) (ci-dessus en bleu). Par le théorème de Hjelmslev, on sait que \(h=bac\) et \(h_1=b_1ac_1\) sont toutes les deux orthogonales à la droite \((BC)\). On note \(h_A, E_a\) les pieds de perpendiculaire sur \((BC)\). En utilisant les définitions de \(B\) et \(C\), on peut écrire \(Bh=Bbac=b_1ac=b_1ac_1C =h_1C\). En notant \(u\) et \(v\) les perpendiculaires à \((BC)\) en \(B\) et \(C\) (en vert foncé ci-dessus), de \((BC)=uB=vC=Cv\), on tire \(uh=h_1v\).
Soit alors \(J\) un point tel que \(B^J=C\) (\(J\) un milieu de \(B,C\)), par conservation de l’orthogonalité des symétries centrales, on a \(Ju=vJ\). Le produit des deux égalités donne \(Jh=vJh_1v\). Mais comme \((BC) \mid v, v1, J\) (th 11 préliminaire au théorème de Hjelmslev), on sait que \(vJh_1\) est un point que l’on peut remplacer par son inverse \(h_1Jv\) dans l’égalité, et ainsi \(Jh=h_1J\). En particulier, en se limitant à la droite \((BC)\), avec les pieds des perpendiculaires, il vient \(Jh_A= E_aJ\), soit \(h_A^J= E_a\), autrement dit \(J\) est milieu des points \(h_A, E_a\) … ce qui est illustré avec la distance dans le disque de Poincaré.
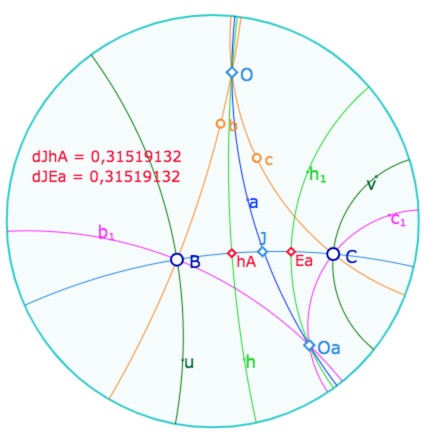
Même configuration avec les deux pinceaux \(\mathscr{P}_{bc}\) et \(\mathscr{P}_{b_1c_1}\) à centre.
Pour cela déplacer les points \(b, \,c\) ou les points \(B, \,C\).
Ouvrir cette figure dans un nouvel onglet
Preuve du théorème pour les points de
contact des cercles exinscrits
Propriété générique et preuve spécifique à la version euclidienne
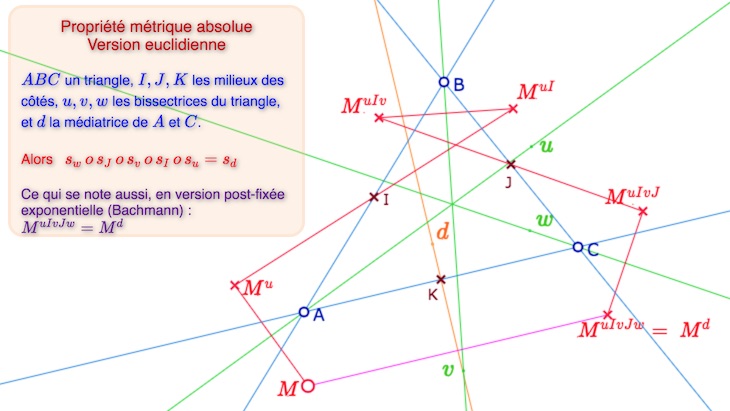
Lancer cette figure dans un nouvel onglet
Preuve euclidienne
D’une manière générale, la droite \((AC)\) est globalement invariante par la composée des 5 isométries. et cette composée transforme \(A\) en \(C\). Cela ne peut être que la symétrie centrale de centre \(K\) ou la symétrie orthogonale d’axe la médiatrice de \(A\) et \(C\). Mais comme il y a trois symétries orthogonales et deux symétries centrales, en passant au vectorialisé (la spécificité euclidienne), la symétrie centrale est exclue, c’est donc la symétrie orthogonale en \(s_d\).
Version absolue de cette propriété
Lancer cette figure dans un nouvel onglet
Preuve de la version absolue
On a ajouté les droites médiatrices du triangle passant par le (un) milieu de chaque côté. En notant en \(a, b, c\) les droites du triangle, opposées à en \(A, B, C\). On a donc en \(I=\Delta_I c= c \Delta_I\), puis \(J=\Delta_J b= b \Delta_J\) et \(K=\Delta_K a= a \Delta_K\). La définition des bissectrices s’exprime aussi sous la forme \(au=uc, cv=vb\) et , \(bw=wa\).
On s’intéresse donc à l’isométrie \(\alpha = uIvJw\). On peut écrire \(\alpha = u\Delta_Iv\Delta_Jw\). On a ainsi \(a \alpha a = uc\Delta_Iv\Delta_Jbw = uIvJw = \alpha\), soit encore \(\alpha^a=\alpha\). On pourrait facilement conclure (avec \(B^\alpha = C\)) si on savait que \(\alpha\) est une droite. Pour montrer que \(\alpha\) est une droite, nous allons montrer qu’elle appartient au pinceau \(\mathscr{P}_{\Delta_I\Delta_J}\) en cherchant à calculer le produit \(\Delta_I \alpha \Delta_J\). Pour le moment, on n’a utilisé des médiatrices que leur orthogonalité avec les côtés du triangle mais par leur définition d’axe de symétrie des sommets, en particulier \(B^{\Delta_I}=A\) et \(A^{\Delta_I}=C\).
Or \(\Delta_I \alpha \Delta_J= \Delta_I u \Delta_I v \Delta_J w \Delta_J = u^{\Delta_I} v w^{\Delta_J}\). Ainsi, par \(B^{\Delta_I}=A\) et \(A^{\Delta_I}=C\), il vient \(A \mid u^{\Delta_I}, v, w^{\Delta_J}\), et donc le produit des trois est une droite (axiome A3) et même une droite du pinceau \(\mathscr{P}_{\Delta_I\Delta_J}\) par les théorèmes de transitivité.
Ainsi \(\alpha\) est une droite. Elle est orthogonale à \(a\) (une autre lecture de \(\alpha^a=\alpha\)) et appartient au pinceau des médiatrices c’est donc la (une) médiatrice de \(A\) et \(C\).
Conséquence sur les contacts des cercles exinscrits
On reprend les notations de la première figure : La propriété précédente permet alors d’écrire \(F_c=D_b^{\Delta_K}\), d’où il vient \(F_c=D_b^K\).
Les points de contact des cercles exinscrits d’un triangle sont symétriques par rapport au(x) milieu(x) des sommets du triangle associés.
Illustrations elliptiques
Dans la figure suivante, on s’intéresse aux points sur la droite \((AC)\). On a noté \(I\) et \(I_2\) les deux milieux des points \(A\) et \(C\). Ces deux points, \(I\) et \(I_2\), sont tous les deux milieux de \(E_c\) et \(h_C\) d’une part, et de \(F_c\) et \(D_c\) d’autre part.
Illustrations statiques
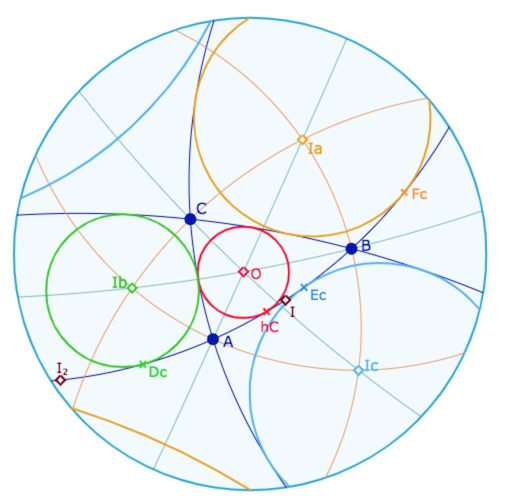
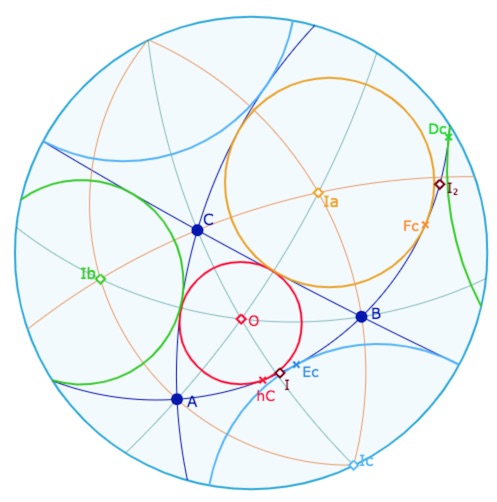
La figure elliptique dynamique
Déplacer les sommets \(A, B, C\).
Lancer cette figure dans un nouvel onglet.