On s’est déjà intéressé aux triangles hyperboliques ayant trois horicycles exinscrits. On se propose ici de calculer les différentes longueurs intervenant dans cette figure. On va effectuer ce calcul dans le modèle du disque de Klein-Beltrami. Comme les distances des différents modèles sont proportionnelles, le calcul est, finalement, générique.
Le contexte est donc celui-ci : on trace les hauteurs d’un triangle dont les sommets sont trois points idéaux \(M, N, P\), et on s’intéresse à son triangle podaire \(ABC\). On se propose de montrer ces différents résultats numériques :
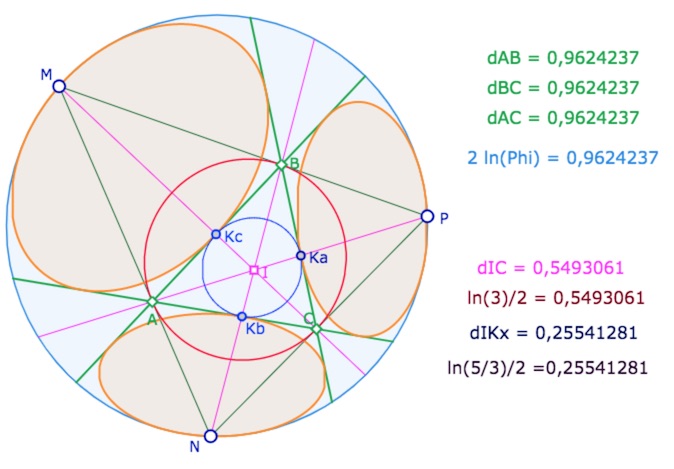
Ouvrir cette figure dans un nouvel onglet.
On sait, d’une manière générale (Th 25 de cette page), que l’orthocentre \(I\) de \(MNP\) est aussi le centre du cercle inscrit du triangle podaire \(ABC\) associé. Mais dans cette figure spécifique, le cercle inscrit à \(MNP\) est aussi cercle circonscrit à \(ABC\). En effet la perpendiculaire à un côté de \(MNP\) issu du sommet idéal opposé est à la fois hauteur du triangle idéal, mais aussi axe de symétrie des deux côtés du triangle et donc bissectrice du triangle idéal. Il en résulte que \(I\) est non seulement centre du cercle inscrit à \(ABC\) mais aussi centre du cercle inscrit à \(MNP\) et donc centre du cercle circonscrit à \(ABC\). Autrement dit le triangle \(ABC\) est équilatéral. Une autre façon présenter ce résultat aurait été de dire que les droites de \(MNP\) et \(ABC\) ont les hauteurs de \(MNP\) comme perpendiculaires communes.
Longueur des côtés du triangle podaire
Pour ce qui est des calculs on envoie le centre \(I\) du cercle en le centre \(O_{hz}\) du disque de Poincaré par une symétrie orthogonale hyperbolique (droite orange ci-dessous), ce qui transforme le triangle \(ABC\) en un triangle \(A_1B_1C_ 1\). On se propose de calculer les longueurs des côtés de ce triangle. Bien entendu le triangle \(A_1B_1C_ 1\) est aussi équilatéral, et donc sa hauteur \((A_1K)\) est aussi médiane, médiatrice, bissectrice.
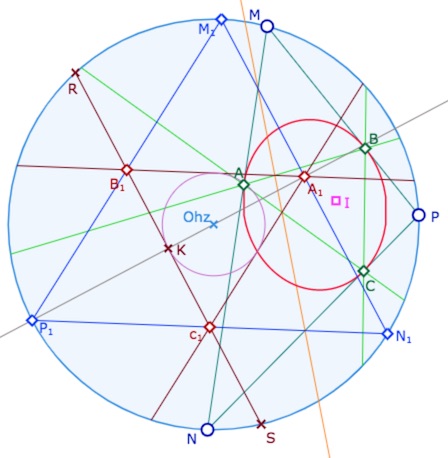
On peut supposer le cercle horizon de rayon 1. Pour calculer les longueurs hyperboliques, on travaille dans le contexte euclidien. Ainsi le triangle \(M_1N_1P_ 1\), image par la même symétrie orthogonale hyperbolique que ci-dessus, de \(MNP\) est équilatéral et donc ses côtés mesurent \(\sqrt{3}\). Il en résulte que les côtés du triangle des milieux \(A_1B_1C_ 1\) mesurent la moitié. Un calcul rapide montre aussi que \(\displaystyle O_{hz}A_1=\frac{1}{2}\) et donc \(\displaystyle O_{hz}K=\frac{1}{4}\).
Pour rappel, dans ce modèle, la distance hyperbolique des deux points \(B_1\) et \(C_1\) est donnée par \(d(B_1,C_1) = \displaystyle \frac{1}{2} \left\vert ln \left(\frac{B_1R}{B_1S} : \frac{C_1R}{C_1S}\right) \right \vert\).
On commence par calculer \(\displaystyle KR=KS=\frac{\sqrt{15}}{4}\). Il en résulte que \(\displaystyle B_1S=\frac{\sqrt{15}+\sqrt{3}}{4}\) et \(\displaystyle B_1R=\frac{\sqrt{15}-\sqrt{3}}{4}\). Comme, par symétrie, \(\displaystyle \frac{C_1R}{C_1S} = \frac{B_1S}{B_1R}\), on peut écrire \(d(B_1,C_1) = \displaystyle \frac{1}{2} . 2 \, ln \left(\frac{\sqrt{15}+\sqrt{3}}{\sqrt{15}-\sqrt{3}} \right)\), soit, après simplification \(d(B_1,C_1) = \displaystyle ln \, \varphi^2 = 2 \, ln \, \varphi\), où \(\varphi\) est le nombre d’or \(\displaystyle \varphi=\frac{1+\sqrt{5}}{2}\).
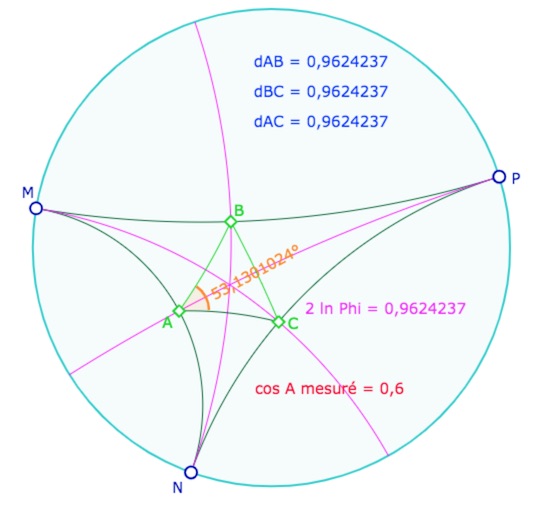
Ainsi le triangle original \(ABC\) est équilatéral, de côté de longueur \(2 \, ln \, \varphi\), indépendamment de la position des points \(M, N, P\).
Enfin, de par \(\displaystyle O_{hz}A_1=\frac{1}{2}\) et donc \(\displaystyle O_{hz}K=\frac{1}{4}\), il vient, de la même façon \(\displaystyle IA=IB=IC = \frac{ln \, 3}{2}\) et \(IK_a=IK_b=IK_c =\displaystyle \frac{1}{2} ln \left( \frac{5}{3} \right)\).
Angle du triangle équilatéral
Calcul numérique
On connait les formules de trigonométrie hyperbolique – présentées par exemple à la fin du premier article sur le mémoire de Bolyaï – et donc, appliquées au triangle équilatéral \(ABC\), il vient :
\(cos \, A : \displaystyle \frac{ch^2 \, a-ch\, a}{sh^2\, a} = \frac{ch \, a}{sh \, a}.\frac{ch \, a -1}{sh \, a} =\displaystyle \frac{th \displaystyle \frac{a}{2}}{th \, a}\).
Ici \(a=ln \, \varphi^2\), d’où \(ch \, a = \displaystyle \frac{\varphi^2+\varphi^{-2}}{2}= \displaystyle\frac{3}{2}\) et \(sh \, a = \displaystyle \frac{\varphi^2-\varphi^{-2}}{2}=\varphi-\displaystyle \frac{1}{2}\).
\(cos A= \displaystyle \frac{3}{2}. \frac{1}{2(\varphi- \displaystyle \frac{1}{2})^2}=\frac{3}{5}\) car \(\varphi^2-\varphi =1\)
Mesure de l’angle sur la figure
On sait que seuls les angles dont le sommet est le centre du disque de Klein-Beltrami sont conformes. Donc pour mesurer l’angle en \(A\), on transporte le triangle \(ABC\) en un triangle isométrique de sommet \(O_{Hz}\) par la symétrie orthogonale d’axe la médiatrice de \(O_{Hz}\) et \(A\). On mesure ainsi l’angle \(im_BO_{Hz}im_C\) et son cosinus … coïncide bien avec la valeur calculée ci-dessus.
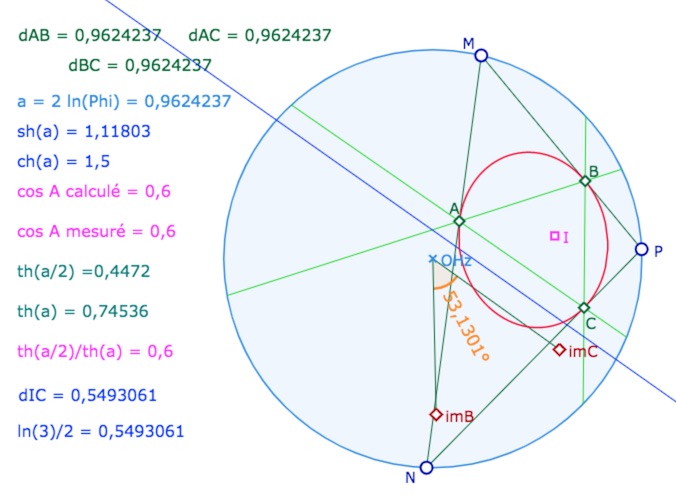
Le cosinus de l’angle du triangle podaire \(ABC\) d’un triangle idéal \(MNP\) mesure 0,6.
Ouvrir cette figure dans un nouvel onglet.
La figure dans d’autres modèles
Construite dans KB, la figure s’envoie naturellement sur la pseudosphère par les macros de conjugaison déjà détaillées ici. On obtient rapidement ce type de figure, dans laquelle on a choisi de prendre un des points idéaux fixe : le seul point accessible par la pseudosphère, le point \(I_{dl}, \; dl\) pour disque limite :
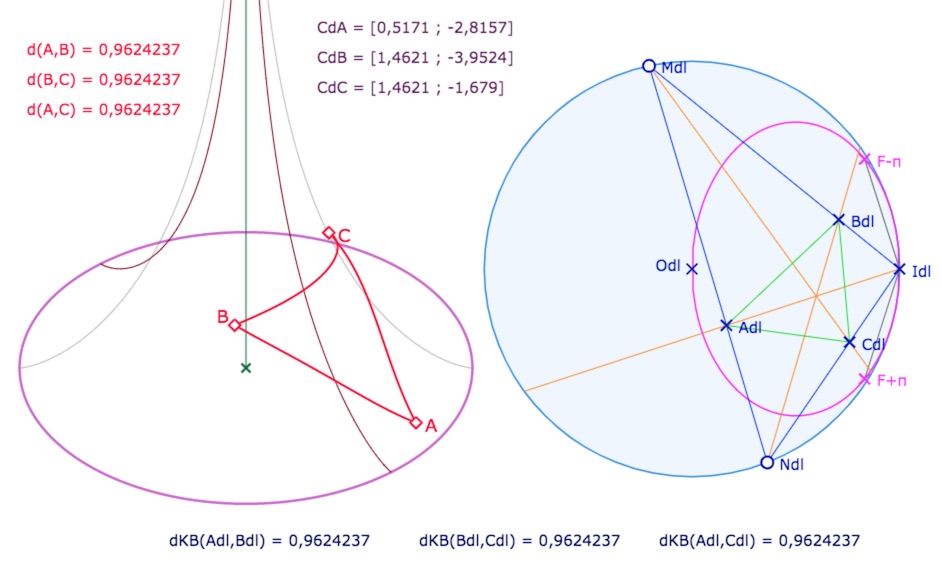
En pratique, dans la figure, on peut déplacer les points idéaux \(M_{dl}\) et \(N_{dl}\) ce qui éloigne les points \(A, B, C\) de l’équateur, et peut même faire enrouler le triangle \(ABC\) autour de la pseudosphère vu qu’il garde les mêmes dimensions.

Ouvrir cette figure (assez grande) dans un nouvel onglet
Bien entendu, on peut faire la même figure dans le disque de Poincaré. On rappelle que la distance est alors (avec les notations usuelles, les points mentionnés sont les points idéaux de la droite hyperbolique) : \(d(A,B) = \displaystyle \left\vert ln \left(\frac{AR}{AS} : \frac{BR}{BS}\right) \right \vert\), sans le facteur \( \displaystyle \frac{1}{2}\) de la distance dans KB.
Ouvrir cette figure dans un nouvel onglet.