La différence entre KH et le plongement de DP (disque de Poincaré) au sens de Bachmann est seulement à l’intérieur du cercle horizon. On peut en particulier appliquer des macros de KH sur les droites idéales de Bachmann. C’est ce que l’on se propose de faire ici.
Cet article comprend plusieurs parties différentes. La première est assez technique et peut être zappée si on ne se sent pas concerné. Les suivantes correspondent bien à ce que l’on attend du titre.
Construction dynamique d’une droite idéale
propre dans le plongement de DP
Tout d’abord, commençons par la construction d’une droite idéale dynamique, essentiellement « propre ». Comme cela est arrivé à différents endroits de ce site – en particulier pour le modèle non arguésien de Hilbert – nous allons à nouveau être confronté à cette différence qu’il y a entre parler, d’un point de vue théorique, d’une droite en général, et aborder la construction de cette droite quand elle est définie par deux points.
Dans cette section, il s’agit de construire une droite idéale – du plongement au sens de Bachmann – pour le disque de Poincaré. Concrètement, cette droite est, en général une droite affine, sauf quand elle rencontre le cercle horizon du modèle, c’est alors la droite idéale propre associée. Voici les différentes situations que l’on veut aborder de manière dynamique. C’est bien entendu le point 4 qui va focaliser notre attention.
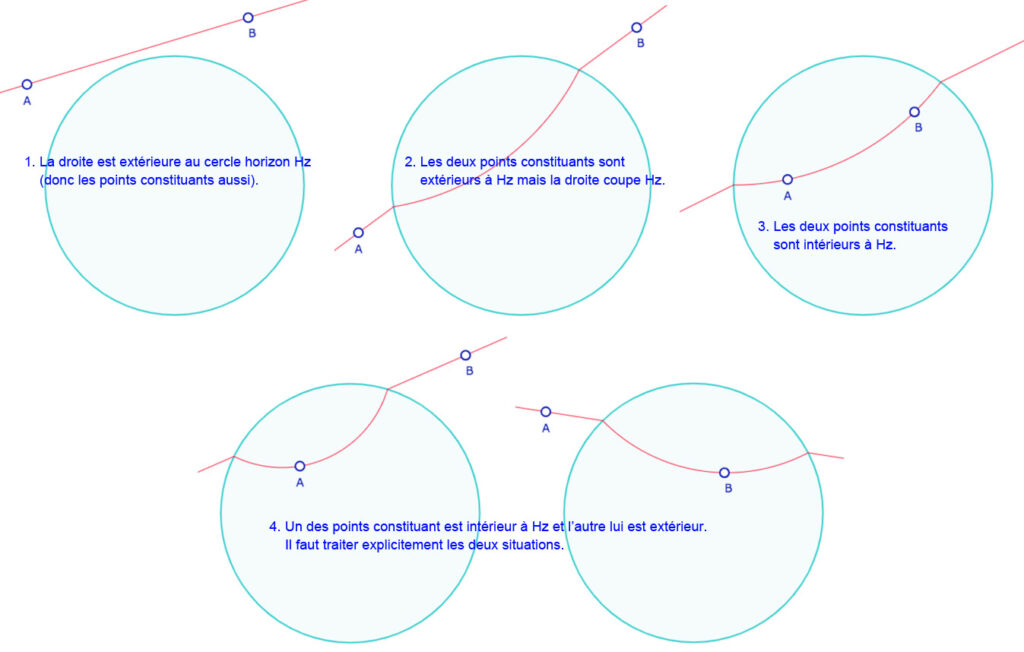
Avant de poursuivre voici une figure manipulable d’un triangle du plongement
Déplacer les trois sommets \(A, B, C\) pour rencontrer les différents cas illustrés ci-dessus.
Comme ce fut le cas pour les perpendiculaires du modèle de Moulton, cette première section est aussi une mémorisation personnelle, sauvegardée ainsi en ligne, des démarches utilisées pour réaliser cette droite idéale générale. Mais cela peut intéresser quelques lecteurs, soit autour de la pratique du logiciel, soit plus généralement, sur la problématique de traiter dans une même procédure (une macro-construction), tous les cas pour rendre compte d’un objet dynamique un peu complexe.
Les lecteurs moins concernés par ces aspects techniques iront directement à la section suivante.
Le cas 1
La droite affine \((AB)\) est toujours construite, mais elle n’est affichée qui si elle ne coupe pas le cercle horizon, ce qui peut se traduire (illustration ci-dessous) par le fait qu’elle est cachée si et seulement si le point \(P_{ee}\) existe, ce qui donne l’expression suivante :

Pour que ce cas 1 soit traité, il suffit que cette expression soit dans la macro-construction.
Les cas 2 et 3
Ce sont encore des cas triviaux déjà rencontrés dans les constructions précédentes.
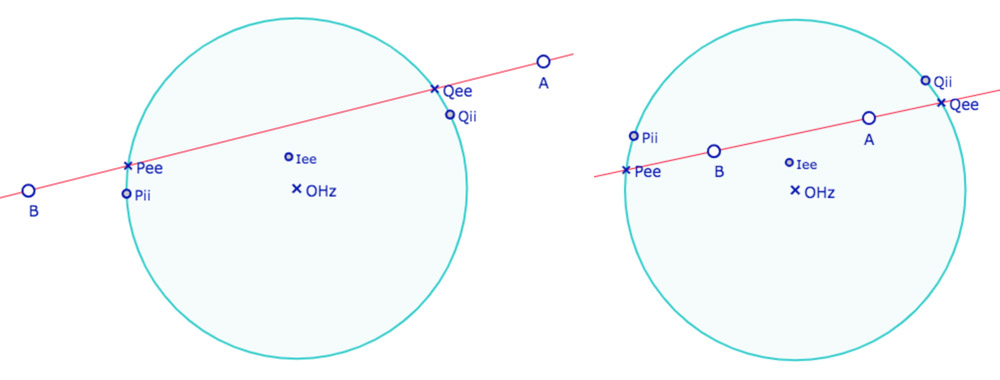
Dans le cas 2, la droite affine \((AB)\) coupe l’horizon en \(P_{ee}\) et \(Q_{ee}\). On construit aussi le point \(I_{ee}\) par lequel passe la droite idéale propre : l’arc de cercle \(P_{ee}I_{ee}Q_{ee}\) est une droite hyperbolique du modèle DP.
Dans le cas 3, \(A\) et \(B\) sont à l’intérieur du cercle horizon \(Hz\), la droite hyperbolique associée passe par les point idéaux du modèle \(P_{ii}\) et \(Q_{ii}\). Il n’y a pas de point \(I_{ii}\) car on prendra (plus loin) le point \(A\).
Le cas 4 – principe de construction
Commençons par voir le principe de construction quand \(B\) est à l’extérieur du cercle et \(A\) à l’intérieur. On veut construire le cercle de centre \(Ctr_{AB}\) passant par \(A\). La droite \((AB)\) est l’axe radical de ce cercle et du cercle horizon. Et la puissance de \(B\) pour ces deux cercles est \(d(B,OHz)^2-Hz^2\).
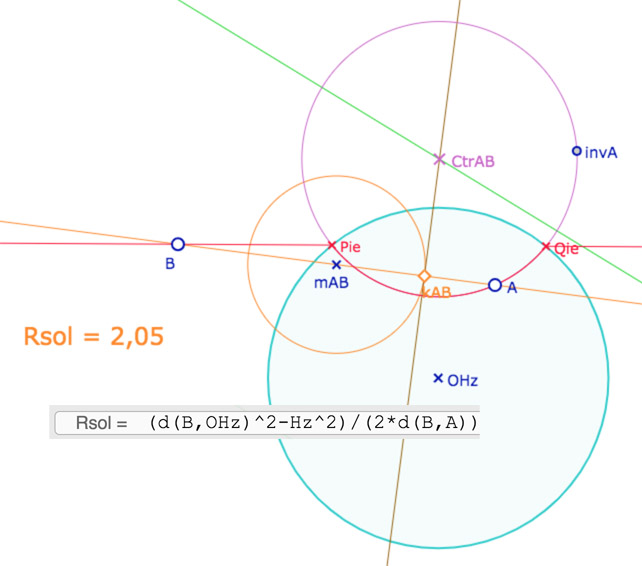
Principe (statique) de la construction
Or on a la formule de la médiane : \(MA^2-MB^2=2\overrightarrow{AB}.\overrightarrow{IM}\) où \(I\) est le milieu de \(A\) et \(B\).
La ligne de niveau associée est la perpendiculaire à \((AB)\) passant par le point \(k_{AB}\) défini par la formule de la médiane. Le centre \(Ctr_{AB}\) du cercle cherché est à la fois sur cette ligne de niveau (marron ci-dessus) et sur la médiatrice (verte) de \(A\) et de son inverse \(invA\) par rapport au cercle horizon – pour être le centre d’une droite hyperbolique de DP.
Sur l’illustration ci-dessus \(k_{AB}\) est une intersection (celle du côté de \(A\)) de la droite \((AB)\) et du cercle de centre \(m_{AB}\), milieu de \(A\) et \(B\), et de rayon \(R_{sol}\) donné par la formule de la médiane. C’est en ce sens que cette construction est statique car elle ne convient que si \(B\) est le point extérieur au cercle et \(A\) intérieur. On construit ensuite le point \(I_{ie}\) comme intersection du cercle et de la demi-droite \([Ctr_{AB}k_{AB})\), troisième point de définition de l’arc cherché.
Le cas 4 – version dynamique
Il faut donc rendre cela dynamique. On remplace le point \(k_{AB}\) par une combinaison linéaire logique entre les deux points, intersections du cercle de centre \(m_{AB}\) et de rayon \(R_{sol}\) adapté (voir plus bas) avec \((AB)\). Ce sont les points \(Kaext\) et \(Kbext\).
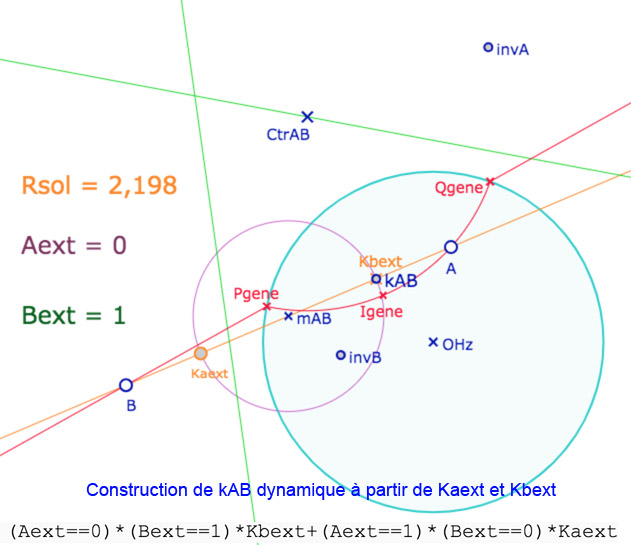
Le centre \(Ctr_{AB}\) est sur la perpendiculaire à \((AB)\) en ce point booléen \(k_{AB}\) et sur une des deux médiatrices, soit de \([A \; invA]\) (ci-dessus), soit de \([B \; invB]\), comme ci-dessous :
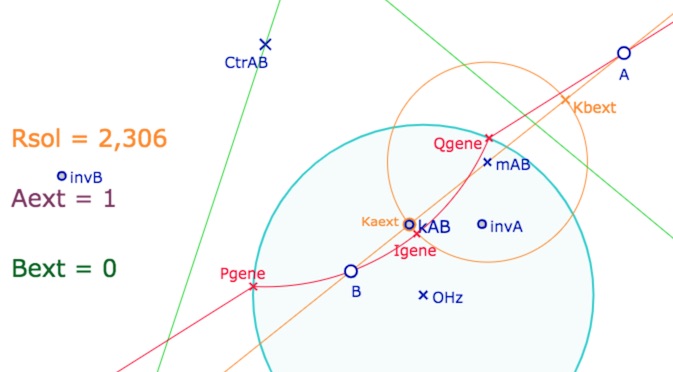
Les points \(Ctr_{AB}\) , mais aussi \(Pgene, Qgene, Igene\) sont des points booléens. La construction n’est pas toujours une combinaison linéaire des différents cas, car quand \(Aext=Bext=1\), les points \(I_{ie}\) ou \(P_{ie}, Q_{ie}\) peuvent ne pas exister. On modifie alors la combinaison linéaire comme ceci :

Cela achève la construction, qu’il suffit de transformer en macro (en n’oubliant pas le cas 1, quand la droite idéale impropre \((AB)\) est la droite affine \((AB)\).
Nouvelle application à Pappus
On a déjà illustré plusieurs fois le théorème de Pappus, y compris dans une version absolue sur les pinceaux comme application de l’antiappariement. On revient sur une version du plongement projectif du disque de Poincaré plus générale que celle proposée antérieurement, en fin de cette page.
Dans cette figure les droites de base sont les droites \((A_1A_2)\) et \((B_1B_2)\). Cela signifie que les points \(A_3\) et \(B_3\) sont des points soit sur la droite affine associée soit sur la demi-droite (de droite) de la droite idéale propre associée.
On peut avoir les trois points d’intersection – alignés – du théorème de Pappus, \(I_1, I_2, I_3\), à l’intérieur ou à l’extérieur du cercle horizon comme ceci :
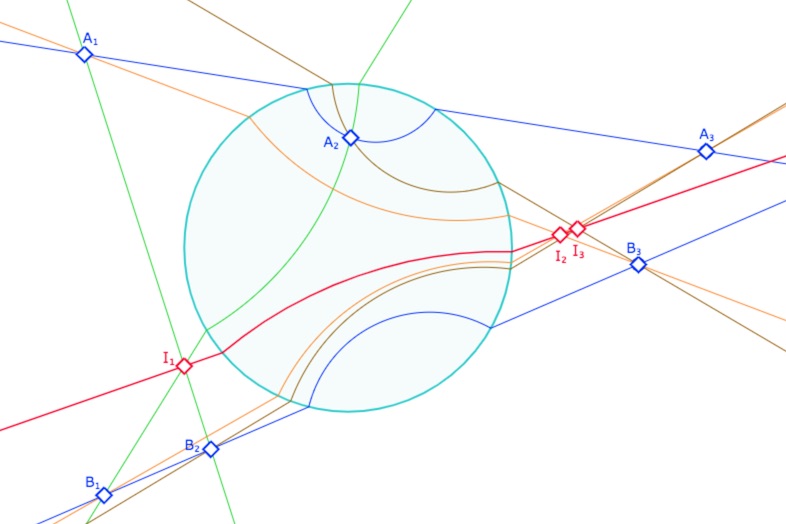
On peut aussi avoir \(I_3\) entre \(I_1\) et \(I_2\).
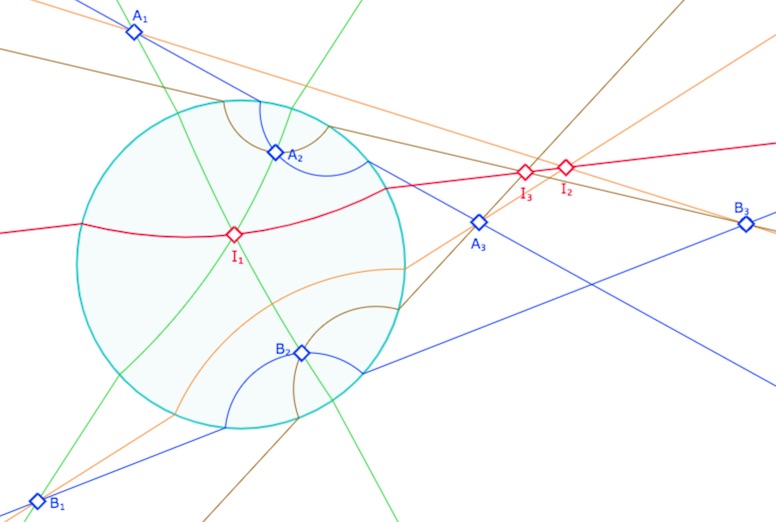
Manipulation de la figure
Même si beaucoup de situations sont traitées, elles ne le sont pas toutes, en particulier quand \(A_1\) et \(A_2\) sont extérieurs au cercle horizon mais que la droite est une droite idéale propre (ie coupe le cercle). D’autres situations ne sont pas traitées (explosion du nombre de cas par inversion des demi-droites constitutives des droites propres).
Agir sur les 6 points bleus, en laissant \(A_1\) à gauche, \(A_3\) à droite et \(A_2\) entre les deux. De même pour les points \(B_1, \, B_2, \, B_3\).
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Les médiatrices d’un triangle
de points impropres dans ce plongement
On aborde désormais la construction de figures usuelles dans le plongement projectif de DP. Cela n’apporte aucune information nouvelle, c’est juste l’occasion de quelques belles illustrations.
On a vu dans la page sur la polarité que dans le cas du disque de Poincaré, l’orthogonalité correspond à la polarité par rapport au cercle horizon : c’est donc la même que dans KH comme présenté dans cette page. On peut alors utiliser certaines macros de KH de cette même page (en particulier la construction des milieux) pour les points que Bachmann a appelé « idéaux impropres » c’est-à-dire extérieurs au cercle horizon. On rappelle – revoir la page d’intro à KH – que deux points ont un milieu (et donc deux) que s’ils sont tous les deux à l’intérieur du cercle horizon (qui sert de cercle unité dans KH) ou tous les deux à l’extérieur. Bien entendu ce qui suit n’a de sens que pour des points idéaux impropres (extérieurs).
En fait la seule différence entre les figures de KH et celles-ci résident dans le fait que le modèle hyperbolique à l’intérieur du cercle est celui du disque de Poincaré et non pas celui du disque de Klein Beltrami. Donc ces figures n’ont rien d’essentiel, elles sont juste un divertissement.
Équivalence entre droites concourantes dans KH et dans DP
On a déjà cité, dans la section « cercles circonscrits » de l’article sur les cercles, cette propriété aussi élémentaire que fondamentale de la géométrie projective munie d’une orthogonalité : trois points sont alignés si et seulement si leurs polaires sont concourantes. Et donc par dualité : trois droites sont concourantes ssi leurs pôles sont alignés (et ils le sont sur la polaire de leur intersection). Daniel Perrin précise même, au tout début de sa partie sur les GNE :
Cette remarque utilise fondamentalement le fait que q est non dégénérée. Il n’y a rien de tel sinon (notamment en euclidien). C’est ce qui justifie que nous traitions séparément le cas euclidien d’une part et les cas elliptique et hyperbolique d’autre part.
Partie 4 – page 27
Dans l’illustration suivante, les deux droites \((AB)\) et \((CD)\)sont sécantes en \(I\). On construit une troisième droite \((EI)\) : on a donc trois droites concourantes en \(I\). On note \(p_{XY}\) le pôle de la droite \((XY)\). Ainsi les trois pôles \(p_{AB}, \; p_{CD}, \; p_{EI}\) sont alignés sur la polaire de \(I\).
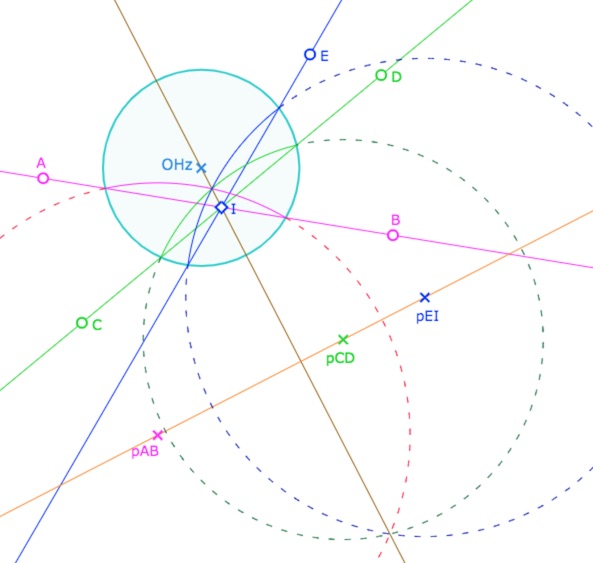
Mais ces pôles sont aussi les centres euclidiens des droites hyperbolique de DP associées – ie ayant comme points idéaux (de DP) les intersections des droites projectives avec le cercle horizon. Or, dans le modèle DP, le concourt de trois droites est équivalent à l’alignement des centres euclidiens associés.
Il n’y a donc aucune surprise à ce que si trois droites de KH sont concourantes, les droites idéales propres « de Bachmann » associées ont leurs parties hyperboliques, (celles du cercle horizon) elles aussi concourantes.
Construction des médiatrices
Pour construire les médiatrices, on utilise la même démarche que l’on a utilisé pour les hauteurs du plongement, présentée aussi à cette page sur la polarité du plongement. On verra une conséquence au paragraphe suivant.
Dans les illustrations suivantes les droites du triangle sont en rouge, les médiatrices passant par les premiers milieux, ceux « euclidiennement entre les sommets » sont en vert, les médiatrices passant par les seconds milieux (indicés 2) sont en bleu.
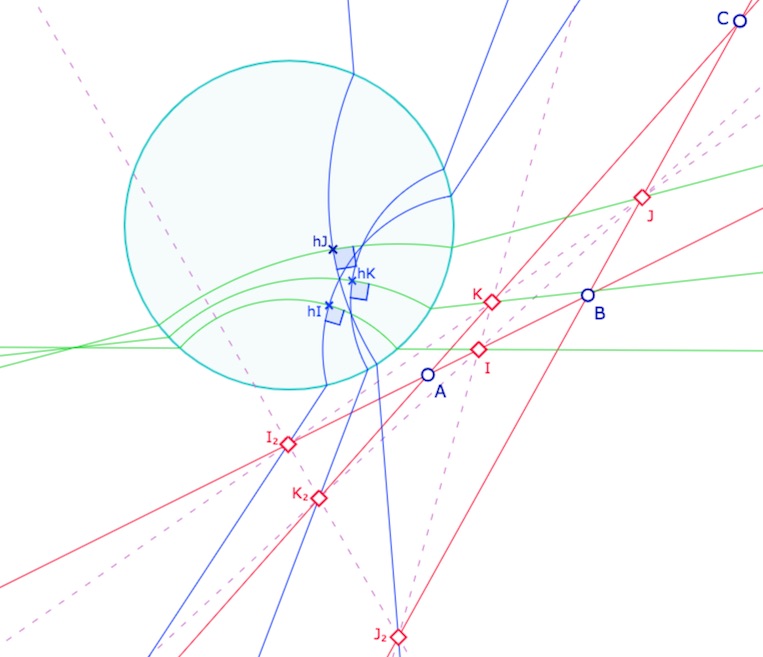
On vérifie que les médiatrices sont concourantes par groupe de trois, les trois vertes ou deux bleues et une verte ( ce qui est trivial car elles le sont dans KH) et que dans DP elles sont bien deux à deux orthogonales en leurs intersections … ce qui est aussi trivial car les milieux sont les centres euclidiens des droites hyperboliques associées : rien de nouveau juste une belle illustration donc.
Voici deux autres illustrations
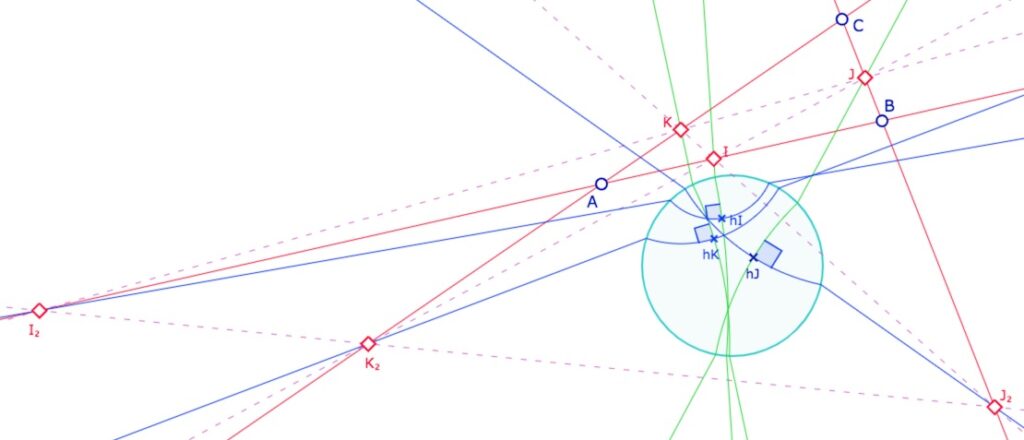
Cas où les trois médiatrices vertes se coupent à l’intérieur du cercle horizon …
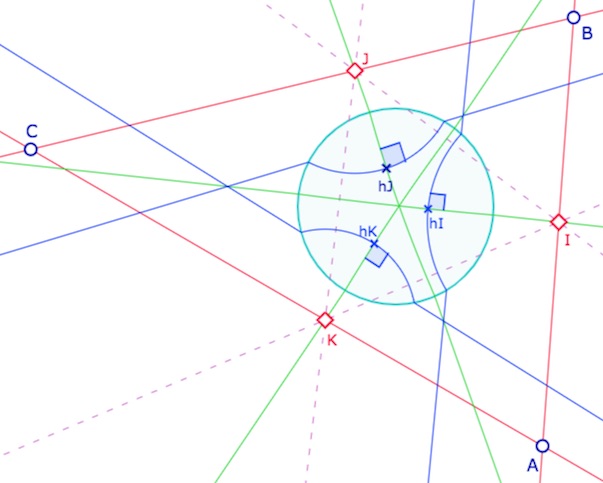
… et ici les trois autres points de concours sont des points idéaux impropres.
Mais bien entendu …
Si l’un des KH-points \(I, J\) ou \(K\) sont dans DP, ils restent des KH-milieux, mais ne sont pas des DP-milieux, en particulier si deux sommets dans dans le cercle horizon. On a bien le concourt des DP-droites, par construction même des perpendiculaires, mais ce ne sont plus des médiatrices … au sens où elles ne passent plus par les milieux.
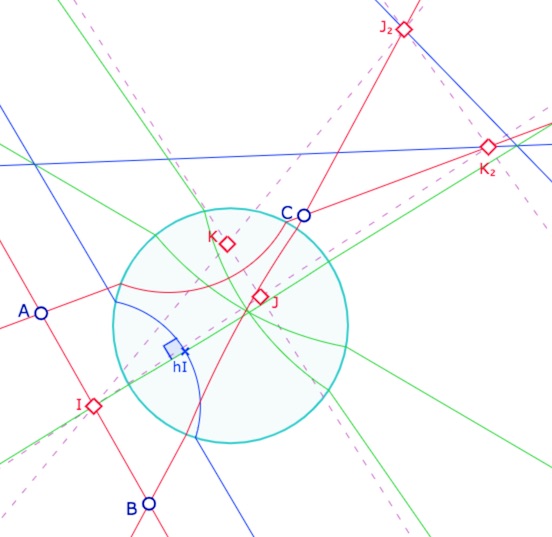
Les limites de la figure : elle n’a de sens que pour les milieux à l’extérieur de l’horizon
Manipulation de la figure
On peut déplacer la figure en translation par un simple clic-glisser
et faire un zoom si nécessaire par deux doigts sur le trackpad (ou sur l’écran d’une tablette).
Agir sur le centre du cercle son rayon et le sommets du triangle.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Cas des médianes
On adapte la figure précédente aux médianes, avec les mêmes contraintes de sens de la figure.
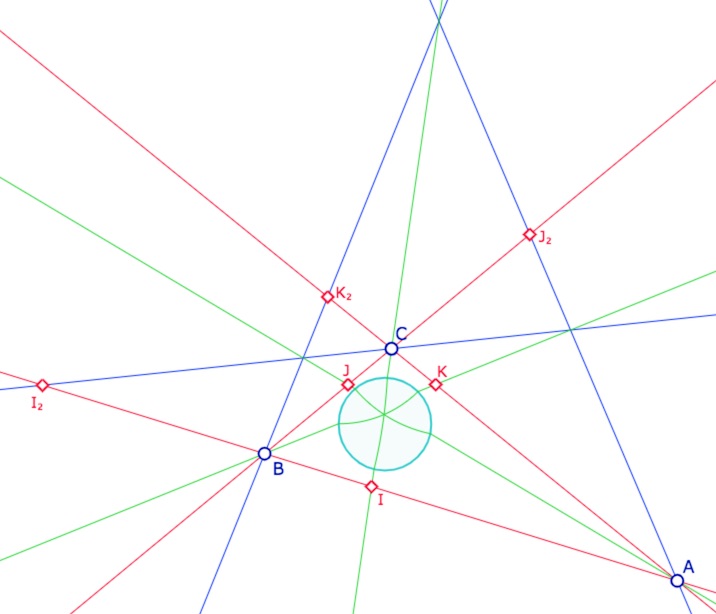
Il faut un petit cercle horizon pour voir les 6 milieux des trois points et voir les 4 intersections de médianes
(ici trois KH-intersections et une DP-intersection)
Ouvrir cette figure dans un nouvel onglet (avec les même consignes que ci-dessus)
Cas des bissectrices
On rappelle que les bissectrices d’un couple de droite n’existent dans KH que si les deux droites coupent, ou ne coupent pas, simultanément, le cercle horizon. Ainsi on a souvent cette situation à une seule bissectrice (on ne construit ici que les bissectrices « intérieures ») :
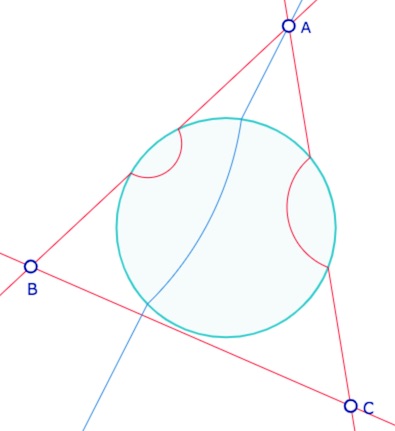
Bissectrice de deux droite idéales propres.
Pas de bissectrice en une droite idéale (générale) et une droite idéale propre
Dans le cas de trois droites idéales propres, on a les trois bissectrices et leur DP-intersection est bien le centre du cercle inscrit aux droites idéales propres comme ci-dessous … quand les trois sommets sont des points idéaux impropres (extérieurs au cercle horizon). C’est, en fait, une autre lecture des DP-bissectrices \((b_1, b_2, b_3)\) d’un DP-trilatère \((a, b, c)\) et de leurs plongements, notés dans la page sur les droites idéales \(g(b_1), g(b_2), g(b_3)\) et \(g(a), g(b), g(c)\).
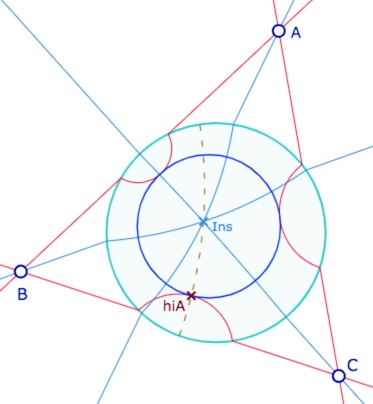
Cette figure n’a de sens que pour les trois sommets extérieurs au cercles, sinon,
par construction la droite issue d’un sommet n’est plus la bissectrice comme ci-dessous en \(C\).
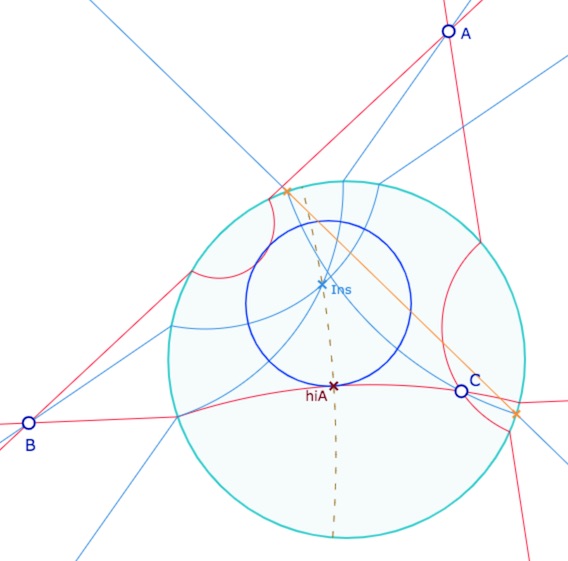
En effet, les bissectrices de deux droites sont les médiatrices de leurs pôles (dernière section de cette page) et par construction de cette droite, passant par \(C\) dans DP, elle n’est plus la KH-bissectrice : cette figure n’a de sens que pour les trois sommets \(A, B, C\) points idéaux impropres du plongement de Bachmann.
Ouvrir cette figure dans un nouvel onglet (sans l’ajout du segment explicatif orange ci-dessus)