Cet article est peut-être plus une mémoire personnelle des méthodes utilisées – pour éventuellement en améliorer certaines – qu’un véritable article de blog. Mais ces méthodes peuvent intéresser quelques personnes. C’est aussi l’occasion de présenter certaines spécificités et/ou fonctionnements internes du logiciel. En terme de mémoire déposée dans le cloud, il s’agit surtout de la construction des perpendiculaires (dernière section) … qui pourrait peut-être être retravaillée.
M-Segment
Le M-segment \([AB]\) a bien entendu pour extrémités \(A\) et \(B\). Mais si les abscisses de \(A\) et \(B\) sont de signes contraires et si la pente de la droite euclidienne est négative, le M-segment n’est plus euclidien, il passe doit passer par le point intermédiaire \(o_{AB}\). On aurait pu construire le M-segment comme réunion de deux segments euclidiens. Comme il existe dans DGPad la notion de liste de segments, on a choisi ce type pour le M-segment. Il faut définir un autre point intermédiaire dans le cas d’un segment euclidien, on a choisi tout simplement le milieu euclidien du segment dans ce cas.
Finalement, on peut simplifier un peu en choisissant comme point intermédiaire \(o_{AB}\) si \(A\) et \(B\) sont de signe contraire (même si la pente est positive) et le milieu des deux points sinon : cela évite de rajouter des tests inutiles. Cela fonctionne aussi même si le segment est vertical dans le repère de base, car la construction du point \(o_{AB}\) a déjà traité cette situation. Le M-segment est donc une liste de trois points, dans le format «liste de de segments», ce qui donne :
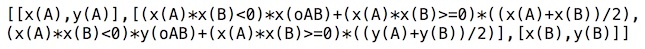
Intersection de deux M-droites
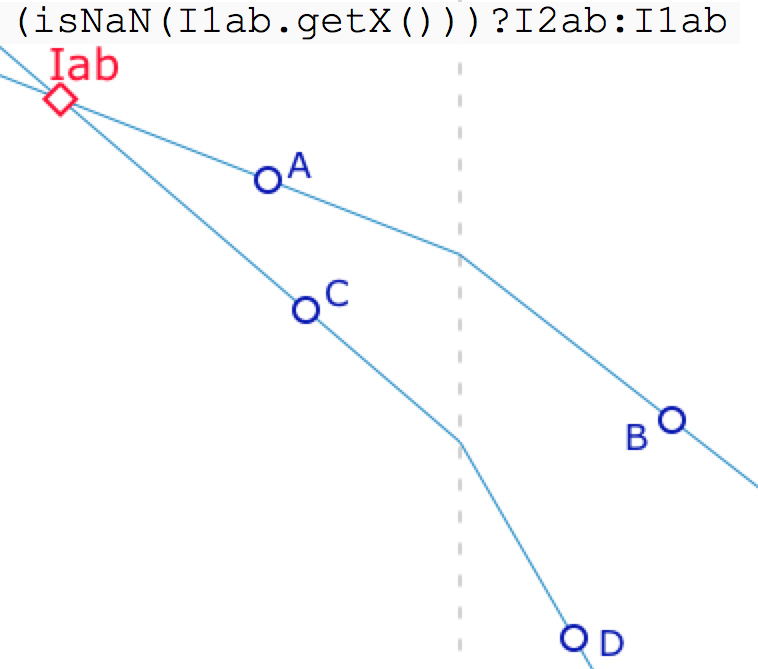
On note \(I_{1ab}\) l’intersection des demi droites d’abscisses négatives et \(I_{2ab}\) celle des demi-droites d’abscisses positives.
Puis on appelle \(I_{ab}\) l’intersection effective des deux M-droites. C’est celui de ces deux points qui existe réellement, son existence étant traitée par gestion d’erreur JavaScript :
si \(I_{1ab}\) n’existe pas, c’est \(I_{2ab}\) sinon c’est \(I_{1ab}\).
Le milieu de deux points A et B
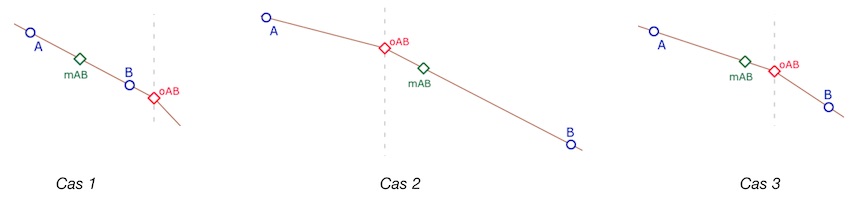
Si les abscisses des points \(A\) et \(B\) ont même signe alors le M-milieu est le milieu euclidien standard \(\displaystyle \frac{A+B}{2}\)
sinon
• si l’origine \(o_{AB}\) est plus près de \(B\) que de \(A\) , le M-milieu est \(o_{AB}+(B-o_{AB})\displaystyle \frac{d(B,o_{AB}-d(A,o_{AB}}{2d(B,o_{AB}}\).
• sinon (si \(o_{AB}\) est plus près de \(A\) que de \(B\)), le M-milieu est \(o_{AB}+(A-o_{AB})\displaystyle \frac{d(A,o_{AB}-d(B,o_{AB}}{2d(A,o_{AB}}\)
ce qui s’écrit tout simplement, en JavaScript :
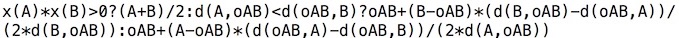
Construction de la parallèle à (AB)
ou [AB] passant par M
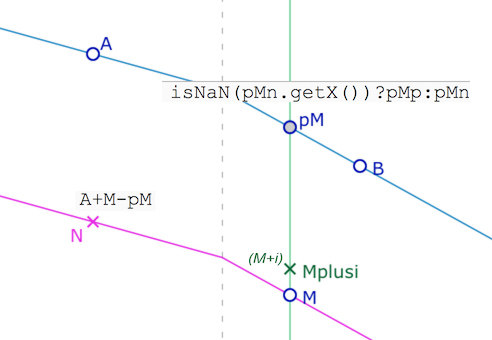
La droite verticale passant par les points \(M\) et \(M+i\) coupe l’une des deux demi-droites euclidiennes constitutives de la droite de Moulton, en \(pM_n\) (d’abscisse négative) ou en \(pM_p\), d’abscisse positive, points non visibles sur l’illustration.
Le point d’intersection dynamique \(pM\) de la droite verticale avec la droite \((AB)\) est construite classiquement à partir du traitement d’erreur de l’inexistence d’un de ces deux points : si \(pM_n\) n’existe pas, c’est \(pM_p\), sinon c’est \(pM_n\).
Le point \(pM\) étant construit, on en déduit le point \(M\) par un calcul barycentrique affine usuel \(N=A+M-p_M\), et la droite cherchée est la droite de Moulton \((MN)\).
Comme le segment est construit autrement, la macro a pour objets initiaux les points \(A\) et \(B\). Cela signifie qu’en interne, même si elle existe déjà, la macro reconstruit la droite de Moulton \((AB)\).
Autre option possible non retenue
L’option de fonction affine par morceaux pour représenter une droite de Moulton a été testée. La construction de la parallèle à une droite est plus pertinente (pas de construction par gestion d’erreur), mais on se heurte à des problèmes avec la transformation en macro-construction de l’intersection de deux droites. Voici une illustration dynamique de cette exploration.
On peut déplacer \(A, B\) et \(M\). Contrairement à la version «deux demi-droites», ici, \(N\) est un point sur toute la parallèle à \((AB)\) passant par \(M\). C’est donc un fonctionnement plus dans l’esprit de la géométrie dynamique que le cas général retenu.
Préférer lancer cette figure dans un nouvel onglet.
L’expression E1 décrit la fonction affine par morceau passant par \(A\) et \(B\) qui représente la droite de Moulton. Sa représentation graphique s’appelle f1. E2 est l’expression de la parallèle à \((AB)\) passant par \(M\). On notera qu’elle utilise f1 et non pas E1. Le point \(pM\) est la projection (verticale) de \(M\) sur la droite \((AB)\). C’est simplement le point de coordonnées \((x(M), E1(x(M))\). De même pour \(pN\).
Remplissage d’un triangle
ou d’un quadrilatère
La démarche consiste à utiliser effectivement un point de plus sur le segment reliant deux points d’un polygone. Il faut que ce point existe dans tous les cas et qu’il soit réellement entre les deux extrémités du segment. En pratique, on utilise la même démarche que pour la construction du segment, en prenant le point \(o_{AB}\) si \(A\) et \(B\) sont d’abscisse de signe contraire, le milieu de \(A\) et \(B\) sinon, soit :
\(\left(x(A)x(B)<0\right)o_{AB}+\left(x(A)x(B) \ge 0 \right)\displaystyle \frac{A+B}{2}\)ce qui donne, en JavaScript :
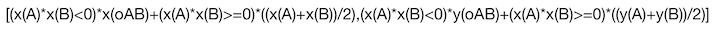
Illustration avec les points intermédiaires
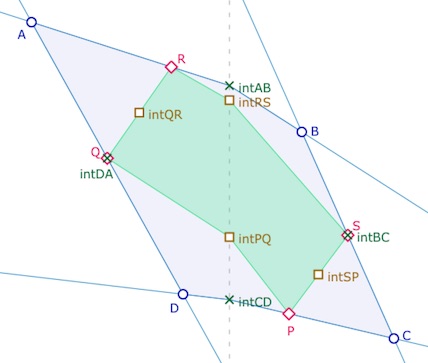
A priori les points intermédiaires des macros sont invisibles (statut interne «totalement caché»). L’illustration ci-contre n’est donc pas reproductible en l’état avec les macros de la page d’utilisation des macros .du plan de Moulton
Ci contre un quadrilatère quelconque \(ABCD\), son quadrilatère des milieux \(PQRS\) et les points intérieurs \(intXY\) de chaque segment, qui sont soit les milieux euclidiens des segments quand les M-segments sont euclidiens, soit les points d’abscisse nulle de ces segments, sinon.
Construction des perpendiculaires
Il y a plusieurs façons de réaliser ces perpendiculaires, depuis une approche totalement algébrique à une approche géométrique. Voici quelques éléments de la méthode retenue pour ces constructions. On s’intéresse donc à la mise en œuvre dynamique de la ou des deux perpendiculaires à la droite de Moulton \((AB)\) issue d’un point \(M\).
Cas des droites à pentes positives. (pABneg>0)
C’est le cas le plus délicat car les perpendiculaires sont des droites de Moulton à pentes négatives donc constituées dans tous les cas de deux demi-droites. Nous présentons en détail le cas de la première perpendiculaire (rose ci-dessous).
La droite \((AB)\) étant constituée de deux demi-droites issues de \(o_{AB}\), on nomme \(H_n\) (\(n\) pour \(x<0\)) et \(H_p\) (\(p\) pour \(x>0\)) les pieds de la perpendiculaire euclidienne à \((AB)\) issue de \(M\) du côté des abscisses négatives et positives respectivement.
La droite \((MH_n)\) coupe la demi droite des ordonnées (\(y<0\)) en \(o_1H_n\) : ce point est le point pour la hauteur issue de \(M\) pour \(x_M<0\).
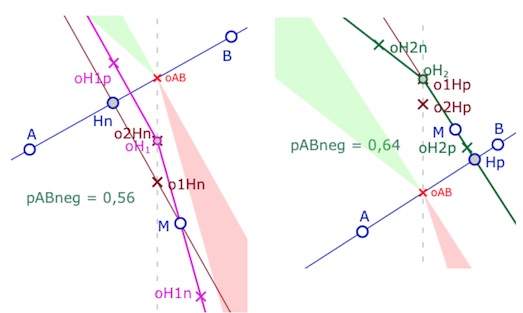
La parallèle à la direction de pente double passant par \(M\) coupe le demi-axe des ordonnées (\(y<0\)) en \(o_2H_n\) : c’est le point de l’axe des ordonnées pour la hauteur issue de \(M\) pour \(x_M>0\). De même, la droite \((MH_p)\) coupe la demi droite des ordonnées (\(y>0\)) en \(o_1H_p\) : le point (\(x=0\)) pour la hauteur pour \(M\) d’abscisse positive. La parallèle à la direction de pente double coupe le demi axe (\(y>0\)) en \(o_2H_p\) : point d’origine de la hauteur si [\(M\) est d’abscisse négative.
La première hauteur (d’origine \(oH_1\)) passe par \(oH_{1p}\) et \(oH_{1n}\), tous trois ainsi définis :
Si \(o_1H_n\) existe et \(x_M<0\) alors \(oH_1=o_1H_n\)
Si \(o_1H_n\) existe et \(x_M>0\) alors \(oH_1=o_2H_n\)
ce qui est résumé (ci-dessous à gauche) dans le test \(\left( y(o_1H_n)>y(o_2H_n) \right)?o1H_n:o_2H_n\)
Dans les deux cas \(oH_{1n}=\displaystyle \left( 1, y(oH_1)- \frac{2}{pABneg} \right) \)
et \(oH_{1p}=\displaystyle \left( -1, y(oH_1)+ \frac{1}{pABneg} \right) \)
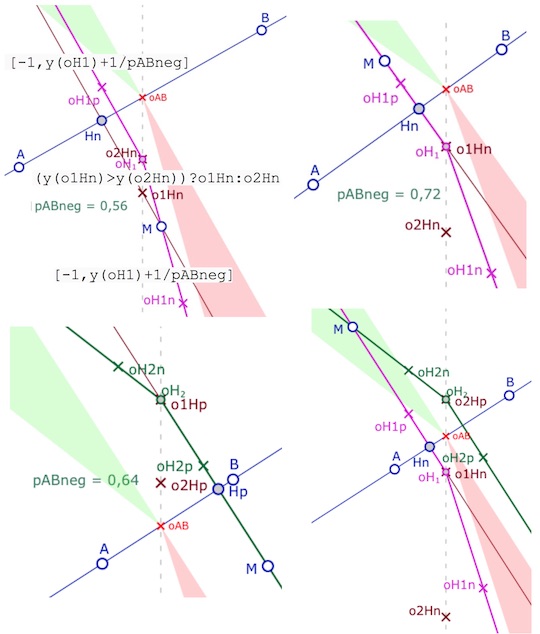
Si \(o_1H_n\) n’existe pas, c’est que \(o_1H_p\) existe. On a envie d’écrire, pour \(o_1H\) la même chose avec, respectivement, \(o_1H_p\) et \(o_2H_p\). Mais les choses ne sont pas aussi simples …
En effet, cette autre perpendiculaire, peut aussi exister avec la précédente, il faut donc avoir une autre origine pour cette autre perpendiculaire, ce sera \(oH_2\) dont la définition est nécessairement plus complexe que celle de \(oH_1\), car \(oH_2\) est à la fois l’origine de la première perpendiculaire quand elle est unique (ci-contre à gauche) et en même temps l’origine de la seconde perpendiculaire (ci-contre à droite) quand les deux existent.
Sa définition est donnée ci-dessous (et les deux dernières illustrations en rendent compte).
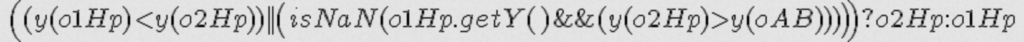
Dans ce cas on a \(oH_{2p}=\displaystyle \left( 1, y(oH_2)- \frac{1}{pABneg} \right) \) et \(oH_{2n}=\displaystyle \left( -1, y(oH_2)+ \frac{2}{pABneg} \right) \), avec une notation plus cohérente que pour \(oH_{1p}\) et \(oH_{1n}\) (sur le signe de l’abscisse).
Cas des droites à pentes négatives. (pABneg<0)
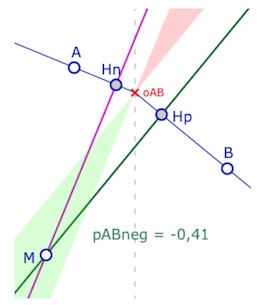
Les perpendiculaires, sont des droites euclidiennes, et donc la situation est très simple, comme ci-contre. Ce sont des droites qui sont nommées \(L_2\) et \(L_4\). La gestion de l’apparition des hauteurs.
En pratique les hauteurs sont toutes toujours construites, et elles sont cachées ou montrées selon le contexte. Dans le cas des perpendiculaires à pente négatives, celle d’origine \(oH_1\) est composée des demi-droites \(R_2\) et \(R_8\). Elles sont toujours affichées quand elles existent. Par contre celle d’origine \(oH_2\), composée des deux demi-droites \(R_9\) et \(R_{10}\) doit être gérée. Cela se fait dans une expression dont le contenu est :
R9.setHidden(pABneg<0);R10.setHidden(pABneg<0);
L2.setHidden(pABneg>0);L4.setHidden(pABneg>0);
Les couleurs des parties «sans/avec 2» perpendiculaires \(psp_{AB}\) et \(pdp_{AB}\)
La couleur ne dépend que du signe de pABneg, ce qui donne, par exemple
(pABneg<0)?Poly1.setRGBColor(255,0,0):Poly1.setRGBColor(50,250,25);
Manipulation de la figure avec tous les points de construction apparents
Figure permettant d’explorer les différentes situations présentées dans cette section
Préférer lancer cette figure dans un nouvel onglet.