Après les pavages réguliers constructibles, puis les pavages orthogonaux non réguliers, cette page s’intéresse à des pavages réguliers \(P(\infty,k)\) qui n’ont plus des cercles comme support, mais des horicyles.
Le principe de la construction
La construction est élémentaire, totalement géométrique et sans calculs. C’est surtout pour une certaine esthétique propre à ces figures que l’on se propose de les présenter dans ce petit article. Comme pour les pavages précédents, on travaille dans le disque de Poincaré.
On se donne un point \(A\) du plan hyperbolique et un point idéal \(I\), soit un point du cercle horizon dans le modèle du disque de Poincaré. On va donc construire des horicycles d’axe \((AI)\). Ainsi, pour le pavage \(P(\infty,k)\) de centre \(I\) de sommet \(A\), on construit l’horicycle tel que le premier arc d’horicycle de sommet \(A\) fasse un angle de \(\displaystyle \frac{\pi}{k}\) avec la droite \((AI)\) de telle sorte que \((AI)\) soit axe de symétrie du polygone infini à construire. Ce qui donne, pour les premières constructions :
Pour \(k=3\)
\(u_A\) est le projeté orthogonal de \(I\) sur la tangente à \((AI)\) en \(A\), ce qui permet de construire l’angle \(\displaystyle \frac{\pi}{3}\) et ainsi construire le premier horicycle de ce pavage, celui de centre \(I\) passant par \(A\). On construit ainsi les deux premiers sommets du polygone autour de \(A\), puis les deux autres horicycles de ce pavage \(P(\infty,3)\), celui de centre \(J\) et celui de centre \(K\).
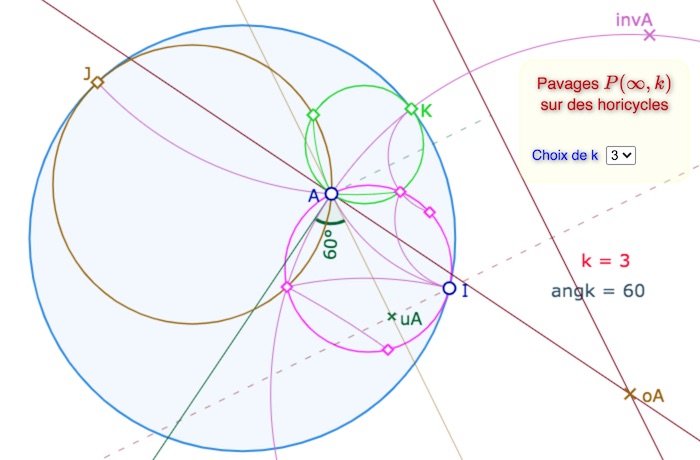
Début de la construction de \(P(\infty,3)\).
On notera que les axes de horicycles se prolongent par des arcs de polygones d’un autre horicycle.
Pour \(k=4\)
Dans ce cas, les pavages sont composés de polygones orthogonaux. Ils ont alors des propriétés plus spécifiques. Par exemple, dans ce cas, les centres d’horicycles \(J\) et \(K\) sont alignés avec \(A\), de même pour les centres \(I\) et \(L\) et les deux droites sont orthogonales. En pratique, \(L\) est l’inverse de \(I\) par rapport à l’arc de cercle \((JK)\).
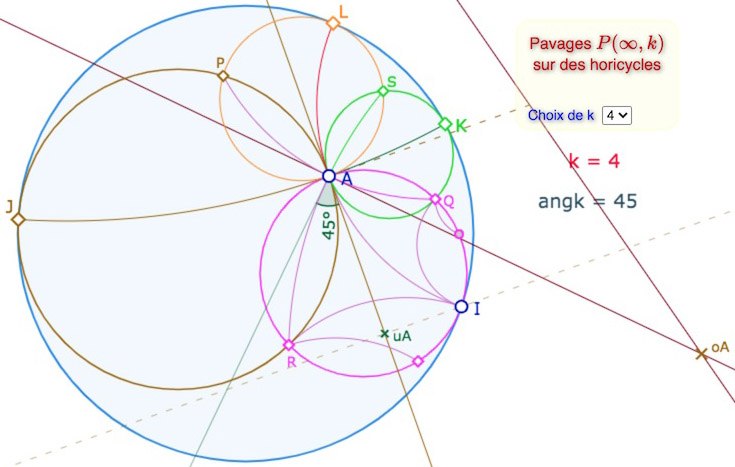
Début de la construction de \(P(\infty,4)\).
De même, les points \(P, A, Q\) sont alignés, ainsi que \(R, A, S\) et les deux droites associées sont orthogonales. Ces droites seront aussi, bien entend, des « droites des centres » dans le cas d’une figure plus aboutie.
Pour \(k=5\)
Il y a donc un horicycle de plus passant par \(A\). Selon la construction, il est avant ou après celui de centre \(L\). Ici on a conservé la construction antérieure de \(L\) (inverse de \(I\) selon \((JA)\)), ce qui fait que le nouvel horicycle, de centre \(M\), est avant celui de centre \(L\) (depuis le point \(I\).
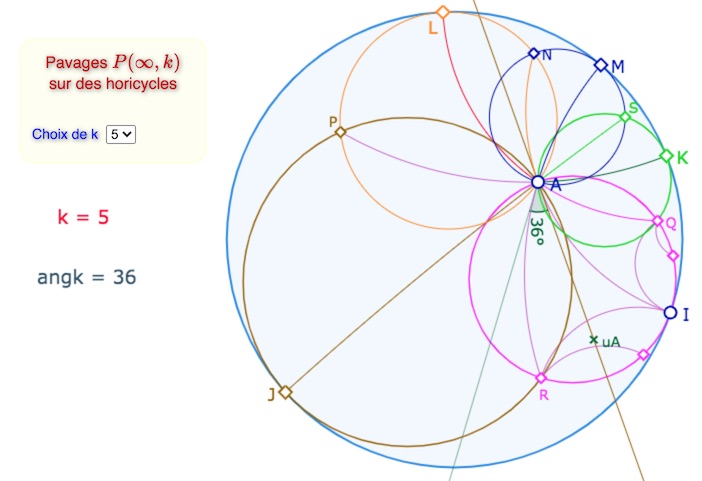
Comme dans le cas impair précédent, les axes des horicycles sont alignés avec les arcs du pavage d’autres horicycles passant par \(A\). Ainsi \(R, A, M\) sont alignés. De même, \(I, A, N\) ou encore \(Q, A, L\) sont alignés ainsi que \(P, A, K\) et \(J, A, S\).
Figure de synthèse
La figure est réglée sur \(k=5\). Pour les autres valeurs, on a laissé volontairement apparaitre les points qui ont été construits postérieurement : tous les points de \(k=5\) ne sont pas cachés pour \(k=4\) ou \(k=3\).
On peut déplacer les points \(A\) et \(I\), ou changer le paramètre \(k\).
Cette première étape étant effectuée, nous allons poursuivre les trois cas dans trois figures différentes, pour aller plus loin dans chaque cas. Bien entendu, les polygones étant sur un horicycle, on ne construit que quelques uns des côtés de chaque polygone, et seulement que quelques sommets de chaque polygone pour la génération 1 du pavage.
Figure de \(P(\infty,3)\)
Dans cette première figure, on a choisi de remplir les triangles idéaux, chaque triangle ayant un point à l’infini et deux points sur un horicycle. L’angle au sommet idéal est nul (indépendamment du modèle, mais, dans ce modèle, les deux arcs de cercles étant orthogonaux au cercle horizon, c’est évident). Les deux autres angles sont de \(\displaystyle \frac{\pi}{5}\).
Préférer ouvrir cette figure (alors bien plus grande) dans un nouvel onglet.
Figure de \(P(\infty,4)\)
Version « horicycles »
On commence par une version où on met en évidence les horicycles avec des débuts de polygones orthogonaux (car \(k=4\)) à un nombre indéfini de côtés, et donc avec quatre angles droits en chaque sommet où les horicycles se rencontrent.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Dans cette figure, comme dans les suivantes, les polygones sont partiels, et en particulier, les deux rayons allant d’un point de l’horicycle à son centre ne sont pas des arcs du polygone.
Version avec des triangles
On peut reprendre, comme pour \(k=3\), une version avec des triangles. Les triangles, ayant un sommet idéal, ont un angle nul et deux angles de \(\displaystyle \frac{\pi}{4}\).
Chaque triangle a donc une aire de \(\displaystyle \frac{\pi}{2}\).
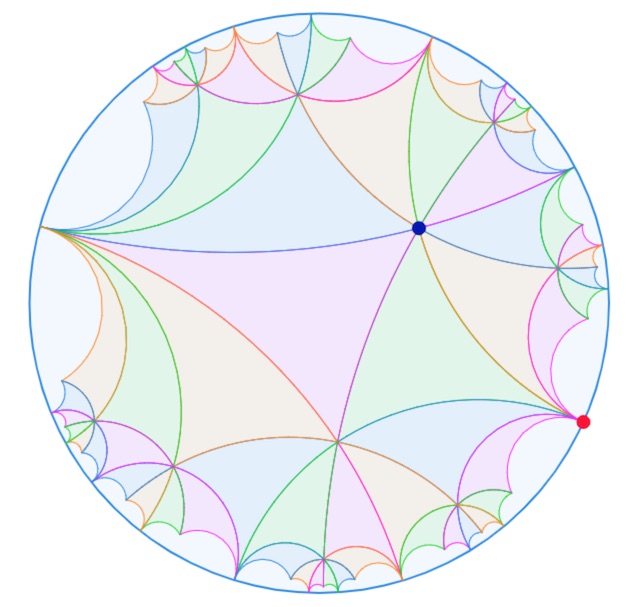
Lancer la figure associée dans un nouvel onglet
Si on associe les triangles par deux, les quadrilatères ont alors une aire de \(\pi\).
Version avec des quadrilatères
On se propose maintenant de construire une figure composée de quadrilatères ayant un point idéal. Ils ont alors tous un angle nul, un angle droit et deux angles de \(\displaystyle \frac{\pi}{4}\). Ne construisant que des quadrilatères, seuls quelques sommets n’auront que 4 angle droits. La plupart auront deux angles droits et quatre angles de \(\displaystyle \frac{\pi}{4}\), parfois trois angles droits et deux de \(\displaystyle \frac{\pi}{4}\).
En déplaçant le point \(A\), repérer les sommets où il y a 4 ou 5 quadrilatères et celui où il y en a 7.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Figure de \(P(\infty,5)\)
On termine ce petit article par une figure du cas de 5 horicycles autour d’un point. On n’a construit que 14 horicycles, soit 5 horicycles autour de 4 points de l’horicycle principal.
Comme dans les autres figures, déplacer les deux points disponibles.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.