Dans la figure de cet article, on vous propose de construire une suite de triangles équilatéraux pour illustrer une approche heuristique de P(3, 7), P(3, 8) et P(3,9), c’est-à-dire de pavages construits à partir de triangles équilatéraux.

Pour cela un plan de construction est proposé dans la galerie suivante. Des points sont nommés pour détailler les actions à effectuer, mais il n’est pas nécessaire de les nommer dans votre construction.
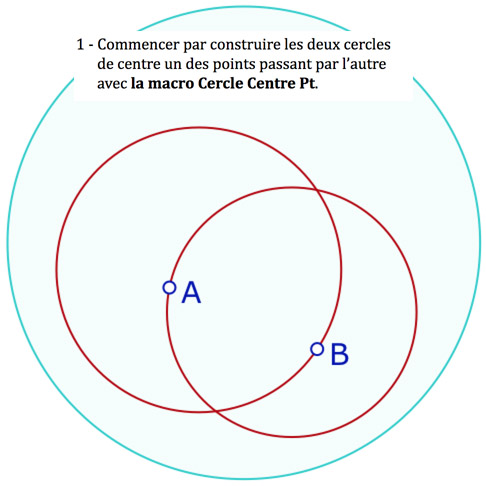
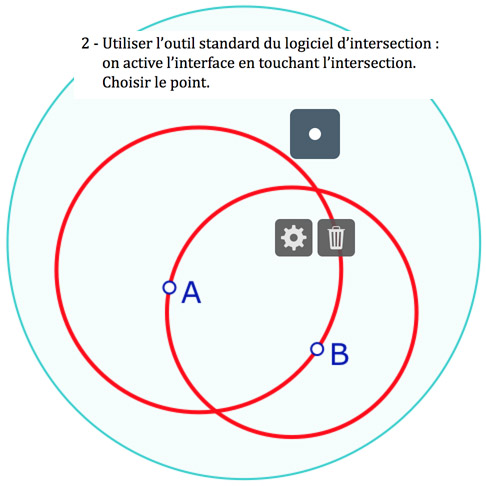
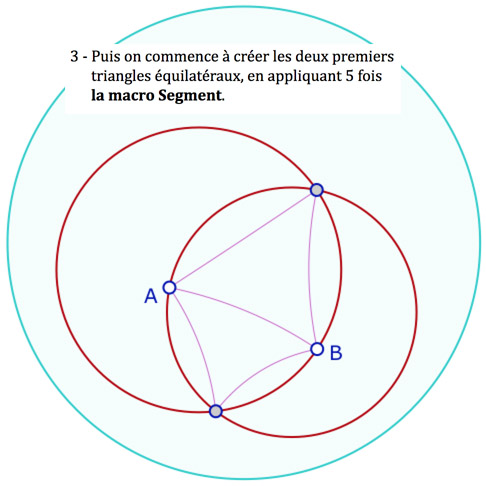
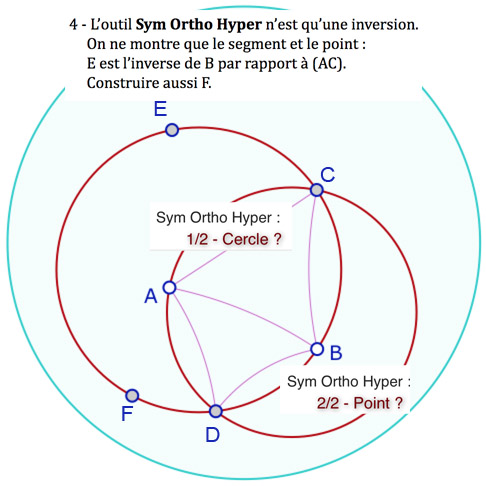
En général on utilise seulement les macro-constructions ci-contre, mais à l’étape 2, il faut utiliser les outils euclidiens : on construit la figure dans un modèle d’où le mélange des deux environnements. Dans l’étape 4, on a renommé Sym Ortho Hyper une macro d’inversion. Elle ne demande pas le cercle horizon, seulement le segment axe de symétrie et le point dont on veut le symétrique. Les trois autres macros nécessitent de montrer d’abord le cercle horizon.
On peut revoir la présentation de l’utilisation des macros à cette page.
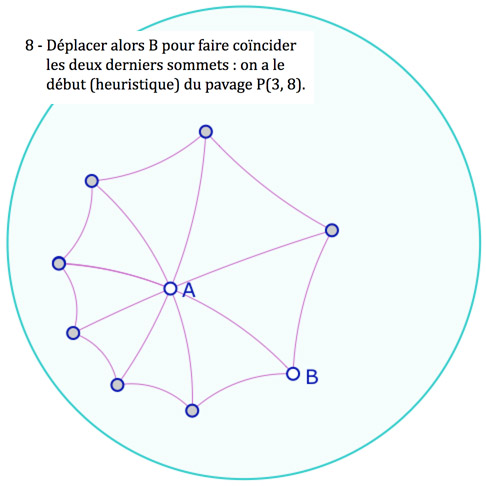
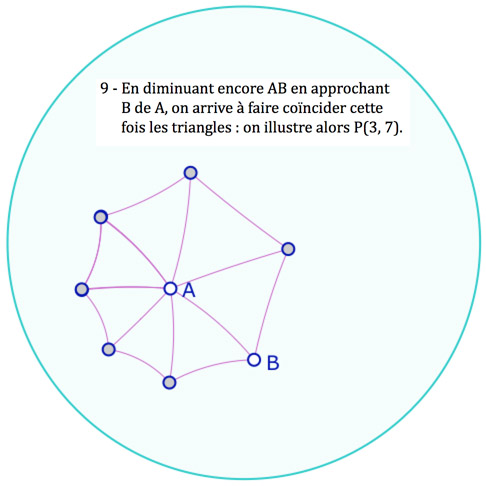
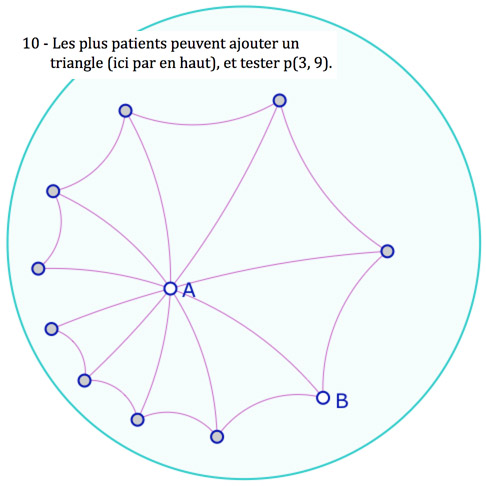
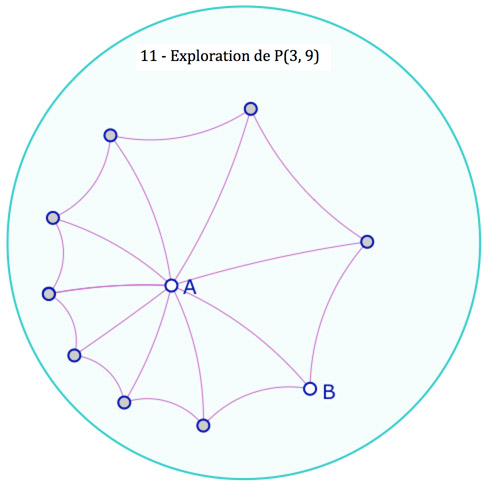
On pourra remarquer que pour P(3, 8) les points opposés sont alignés car on reporte 4 fois 45°. Le pavage P(3, 7) n’est pas constructible à la règle et au compas. Plus généralement, pour ce qui est des angles constructibles, il y a équivalence entre la géométrie hyperbolique et euclidienne .
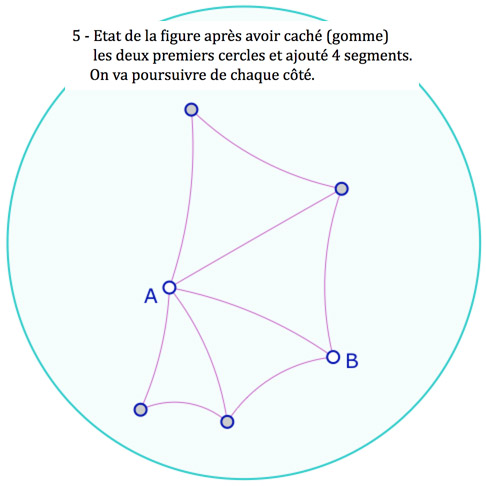
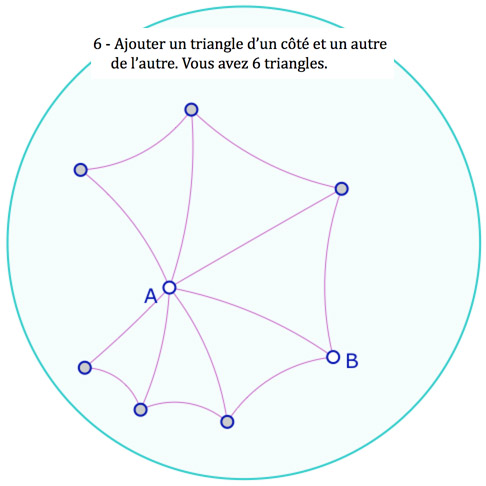
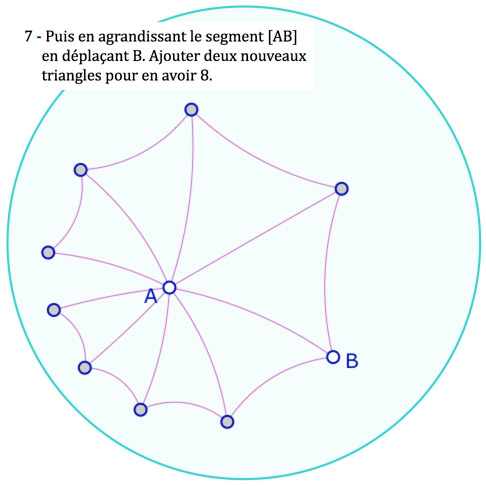
Explorer la galerie de présentation de la construction (11 images) …
… et suivre simplement la procédure proposée dans la galerie
Préférer ouvrir cette figure dans un nouvel onglet.
Réalisation de la génération 2 du vrai pavage hyperbolique P(3,8), à partir de son cercle de pavage. Vous pouvez déplacer le centre O pendant l’animation.
0 commentaire