Dans le menu PSH, on a vu dans les pages sur les pavages que, dans le modèle KB, il était impossible de faire entrer un « vrai pavage » (au moins de génération 1) dans l’équidistante qui représente la PSH. En effet dans le modèle KB, même la génération 1 d’un pavage rempli une grande partie du plan hyperbolique.
Les pavages de KB sont moins esthétiques que ceux du disque de Poincaré. C’est la raison pour laquelle nous allons proposer aux lecteurs, de rentrer dans un autre jeu avec quelques uns de ces pavages, et les construire simplement en quelques clics. Dans un premier temps, regardons le principe de construction. Cette partie technique n’est pas nécessaire pour jouer avec les figures suivantes, c’est juste informatif, pour montrer aussi que c’est assez simple de réaliser ces pavages.
Rappel du principe de construction
des cercles de pavages …
On reprend ce qui avait été expliqué déjà dans cet article sur la construction d’un pentagone orthogonal sur la pseudosphère. Ici on se donne un point centre du cercle, au lieu du point \(A_{kb}\). On reprend les valeurs numériques nécessaires – dont le rayon du cercle de pavage \(r_{45}\) sur la pseudosphère, mais \(2r_{45}\) dans KB car la distance est double dans KB- à la construction d’un point du cercle. Le principe est de construire le pentagone régulier centré en le centre du cercle \(Odl\) car c’est le seul point en lequel les angles sont conformes. On construit donc la médiatrice entre le centre du cercle de pavage et le centre du cercle \(Odl\). On place le point \(r_{KBe}=Odl+2r_{45}enO(uU-Odl)\) qui détermine le rayon de pavage centré en \(Odl\). On termine par le KB-symétrique de \(r_{KBe}\) par rapport à la médiatrice, qui donne le point \(C_{kb}\). Le cercle de pavage – dans l’illustration ci-dessous – est de centre \(A_{kb}\) passant par \(C_{kb}\).
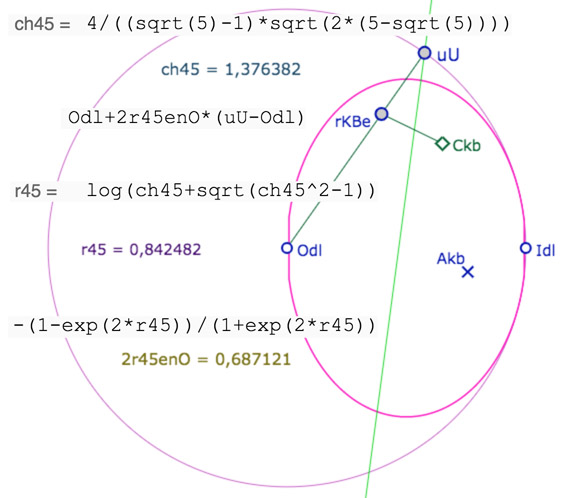
Dans cette illustration, l’ellipse rose est la limite de la pseudopshère dans le « disque limite » de Beltrami.
Le cercle est tracé dans les illustrations suivantes
Un point \(K\) sur ce cercle est envoyé en \(s_K\), à partir duquel on fait un pentagone que l’on renvoie sur le cercle de pavage.
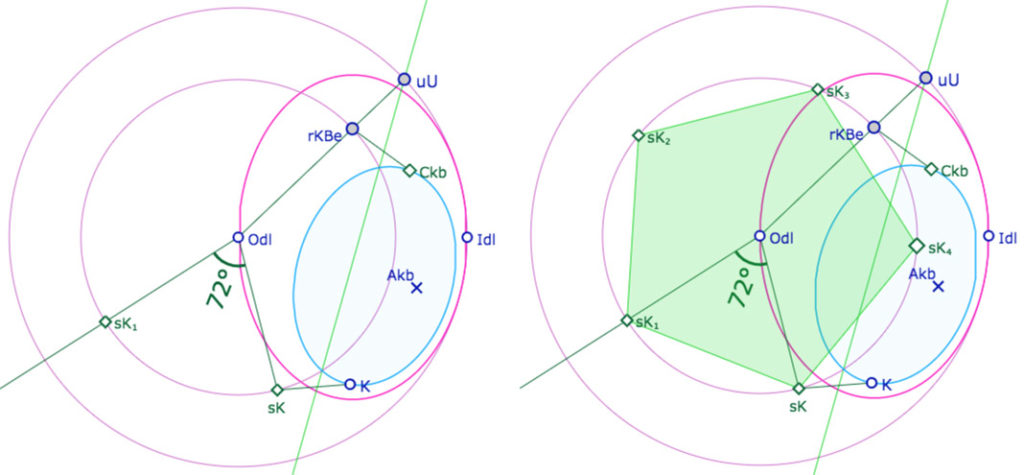
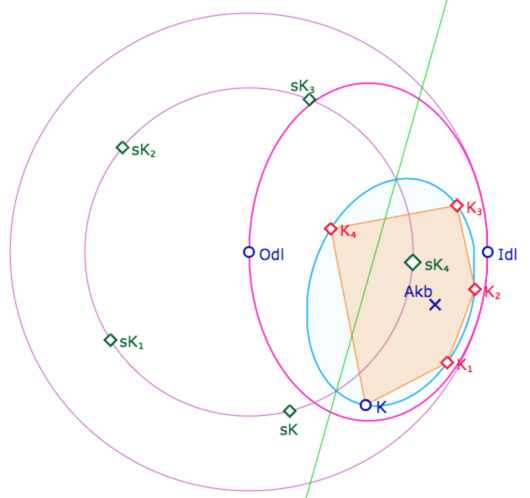
On a donc un pentagone orthogonal modifiable par le point \(K\). Tout ceci est transformé en macro avec comme objets initiaux d’une part la principale valeur numérique nécessaire \(2r_{45}enO\), mais aussi l’angle de 72°, utilisé pour le pentagone, mais qui sera modifié (en 90°) pour que la même macro construise un carré de base de P(4,5) puisque c’est le même cercle de pavage.
Construction des pavages eux mêmes
Là encore on utilise l’idée d’une utilisation optimisée des macro-constructions. Le choix effectué est le suivant, ici illustré sur P(6,4) : pavage d’hexagones orthogonaux. Il s’agit d’utiliser que la symétrie orthogonale est une homologie harmonique : la symétrie orthogonale par rapport à la droite \((K_1K_2)\) est l’homologie harmonique d’axe la droite et de pôle le pôle de la droite par rapport au cercle, soit le point \(Pole_{(K_1K_2)}\). Et on utilise que alors que l’image d’un point est le 4° point de la division harmonique, qui se construit en une ligne algébrique sans plusieurs constructions intermédiaires comme produirait la répétition de nombreuses KB-symétries orthogonales.
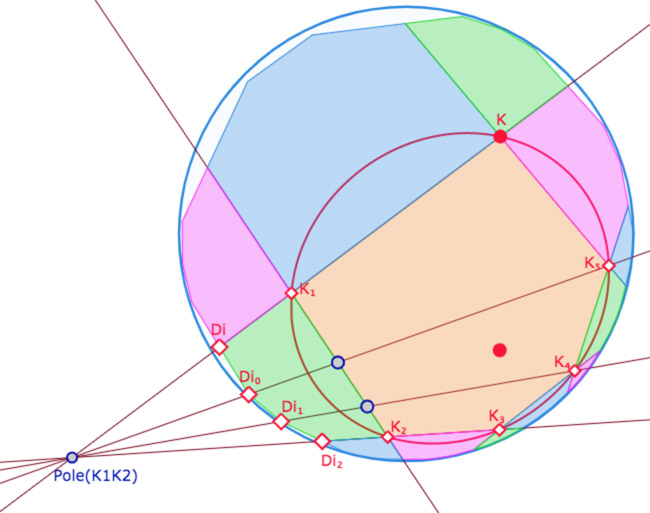
On construit ainsi les 4 points \(D_i, D_{I_0},D_{I_1},D_{I_2}\) images de \(K, K_1, K_2, K_3\). On fait alors une macro qui à partir du cercle horizon et de 6 points d’un hexagone construit l’hexagone symétrique par rapport à la droite passant par les deux premiers points.
La génération 1 des pavages
P54, P45, P64, P46
Dans les quatre cas, on peut agir sur le centre du cercle pendant l’animation sur le point \(K\) (le point bleu). On remarquera l’accélération de l’animation quand \(K\) s’approche de l’horizon (car la distance hyperbolique, à variation euclidienne constante, est plus grande proche de l’horizon.
Génération 1 du pavage P(5, 4) de pentagones orthogonaux
Génération 1 du pavage P(4,5) de carrés à 72°
Génération 1 du pavage P(6, 4) d’hexagones orthogonaux
Génération 1 du pavage P(4,6) de carrés à 60°
Pavages – Jouer avec les macros
C’est essentiellement pour cette partie que cet article a été mis en ligne … juste pour le plaisir de l’immédiateté de ces macros de pavages. On se propose de construire les deux pavages P54 et P45 successivement, dans la même figure … en quelques secondes, puis ensuite sur P64 et P46.
Pour cela , on va donc utiliser les macro-construction du logiciel, comme cela a été présenté dans cette page, mais aussi à nouveau détaillé plus bas, dans le contexte de ces pavages.
Le principe – détaillé sur P54 et P45
Dans la figure suivante, on a le cercle de pavage de P54, rouge, et un pentagone piloté par le point \(M\). On voit aussi les macros disponibles : les macros de division harmonique et de pôle d’une droite, utilisées dans la section précédente, et, pour ce qui nous concerne maintenant, deux macros de pavage.
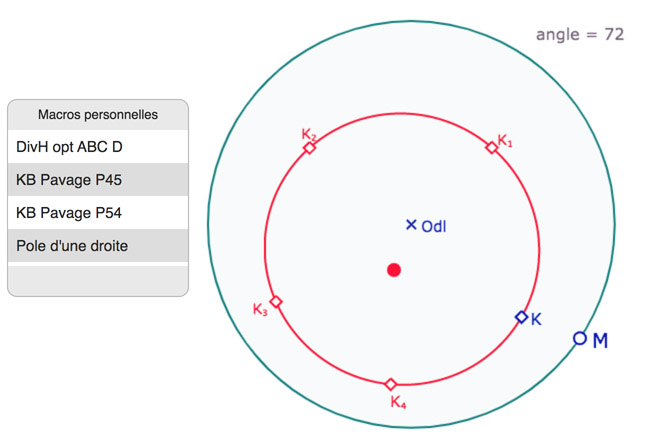
Première utilisation de la figure
• Commencer par déplacer \(M\) sur le cercle horizon pour vérifier que le pentagone de base est piloté par \(M\).
• Puis en sélectionnant l’environnement des macros (icone marteau-clé à molette), lancer la macro KB Pavage P54. Il suffit de montrer le cercle horizon (en cyan) et les 5 points du pentagone \(K, K_1, K_2, K_3, K_4\). La macro construit directement le pavage.
• Vous pouvez déplacer le centre du cercle de pavage et le point \(M\), ou lancer une animation sur \(M\) (30 degrés/s est correct). On peut continuer à déplacer le centre pendant l’animation.
Pour lancer l’animation, il faut revenir en mode standard (la flèche de gauche sélectionnée), puis cliquer sur le point \(M\) et choisir l’outil ressort en bas à droite :
Seconde utilisation de la figure
Il s’agit désormais de montrer pourquoi la réalisation de ces pavages est encore plus simplifiée avec des macros bien choisies. Là, l’idée est de voir pourquoi, dans la macro de disque de pavage, on a choisit d’ajouter l’angle au centre du polygone utilisé alors que c’est a priori inutile. Mais nous allons le modifier pour utiliser le cercle de pavage pour deux pavages.
• Supprimer ce qui vient d’être fait en rechargeant la figure initiale par la première icone de l’iframe.
• Supprimer le dernier point – \( K_4\) – icone corbeille. Quitter aussitôt le mode « suppression » en sélectionnant le mode standard (flèche gauche).
• En mode standard, descendre l’expression angle pour la placer un peu au dessus de \( K_1\).
• Toujours en mode standard, sélectionner – cliquer sur – l’expression angle et choisir l’icone calculatrice.
• Mettre alors l’angle à 90° pour construire des carrés. Ne pas oublier de valider par le bouton vert, puis revenir en mode standard. Remarquer que l’on a bien un carré sur le cercle de pavage.

• Revenir en mode macro, et lancer cette fois la macro KB Pavage P45. Elle demande le cercle horizon et les 4 points \(K, K_1, K_2, K_3\). La macro construit la génération 1 de ce nouveau pavage.
• Vous pouvez à nouveau animer \(M\), et même, en stoppant l’animation, cacher \(M\) (icone gomme) avant de relancer l’animation. Trop fun !
Préférer réaliser ces activités dans une figure en plein écran, (s’ouvre dans un nouvel onglet).
La même activité sur P64 et P46
On peut faire la même chose avec l’autre cercle de pavage, celui de P64 et P46
• Appliquer directement la macro KB Pavage P64 dans la figure ci-dessous.
• Attention : il n’y a pas d’erreur de Promp : pour des raisons de symétrie, après le cercle, il n’y a besoin que des 4 premiers sommets de l’hexagone pour l’application de la macro.
• Éventuellement, animer le point \(M\).
Changement de pavage
• Supprimer ce qui vient d’être fait en rechargeant la figure initiale par la première icone de l’iframe.
• Supprimer les deux derniers points – \( K_4, K_5\) – avec l’icone corbeille. Quitter aussitôt ce mode « suppression » en sélectionnant le mode standard.
• En mode standard, descendre à nouveau l’expression angle (plus pratique pour accéder au mode « expression »).
• Toujours en mode standard, sélectionner – cliquer sur – l’expression angle et choisir l’icone calculatrice (mode « expression ») pour mettre l’angle à 90°. Ne pas oublier de valider avec le bouton vert.
• Puis appliquer la macro KB Pavage P46.
• Éventuellement, animer \(M\) et même cacher le point.
Préférer réaliser ces activités dans une figure en plein écran, (s’ouvre dans un nouvel onglet).
Vous pouvez aussi télécharger les six figures de cet article (sans le mode « restriction ») et les lire en les glissant sur la fenêtre de DGPad en ligne.
Cet article est (aussi) une préparation aux figures de troncatures de pavages dans KB.