Des deux modèles, celui de Hilbert et celui de Moulton, il est bien plus simple de réaliser des figures non arguésiennes dans le plan de Moulton. On peut néanmoins (re)-voir la page sur les macros pour le modèle Hilbert.
Présentation des macros
du plan de Moulton
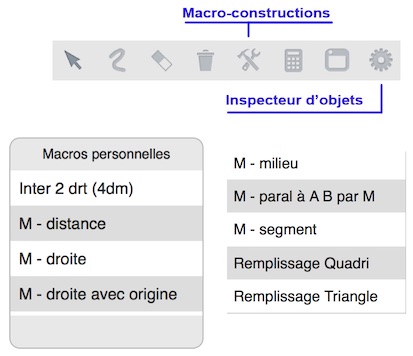
On active les macros par la cinquième icone du tableau de bord. Rappel : présentation de l’utilisation des macros.
Pour le plan de Moulton, on dispose alors de 9 outils que l‘on découvre ci-contre.
L’intersection de deux M-droites
Le premier outil, est la seule macro qui demande comme objets les demi-droites. On montre les deux demi-droites d’une première M-droite, puis les deux de la seconde, dans le même ordre : si on montre d’abord la partie des abscisses positives de la première droite, en troisième objet il faut montrer aussi la partie des abscisses positives de la seconde droite. L’intersection est nommée par défaut Iab. Il faut le renommer dans l’inspecteur d’objet (outil «roue»).
Lancer la figure de base contenant ces macros (dans un nouvel onglet) pour tester les macros.
M-droite, M-droite avec origine, M-segment et M-distance
Ces quatre macros demandent seulement deux points en objets initiaux. Techniquement, les droites et les segments ne sont pas construits de la même façon : une M-droite est la réunion de deux demi-droites depuis le point de l’axe des ordonnées, alors qu’un M-segment est un objet « liste de segments ». La version avec origine rend visible le point sur l’axe des ordonnées. Cela peut servir pour simplifier certaines constructions ou visualiser des alignements. On peut s’amuser à rendre une droite verticale pour voir où est le point d’origine oAB.
Colorisation des droites et des segments : quand on change la couleur d’un M-segment avec l’inspecteur d’objet, le changement n’est pas immédiat, il faut déplacer ensuite un point ou même seulement la figure (dans les deux cas, en mode consultation). Les M-droites étant composées de deux demi-droites, pour changer sa couleur, il faut changer la couleur de chacune de ses demi-droites. C’est instantané.
La macro M-distance donne la longueur du segment entre deux points. On a gardé le terme de distance alors que ce n’est qu’une longueur. On peut facilement refaire cette figure (hors widget s’entend)
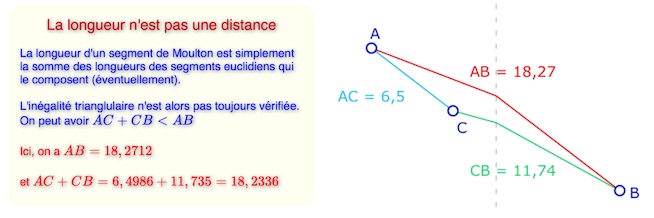
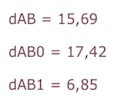
Cette macro renvoie une donnée numérique. Par construction, elle est toujours au même endroit. Il faut donc la déplacer avant de prendre une nouvelle distance. Cela se fait naturellement, à la souris ou au doigt, directement dans le mode macro. Les noms des expressions sont donnés par défaut, comme ci-contre (suffixe numérique incrémenté). Si on souhaite les modifier, il suffit de passer en mode Inspecteur d’objet, puis sélectionner les expressions et changer leurs noms successivement comme ci-dessus.
La parallèle à une droite ou un segment passant par un point
Comme une M-droite et un M-segment sont de nature interne différente, pour que l’on puisse prendre une parallèle indifféremment d’une droite ou d’un segment, on a choisir de devoir montrer d’abord deux points – de la droite ou du segment – puis le point par lequel doit passer la parallèle. Le résultat est une M-droite, composée de deux demi-droites euclidiennes.
Remplissage Triangle – Remplissage Quadrilatère
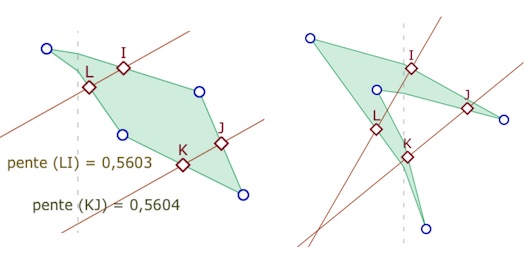
On montre simplement trois ou quatre points. Les M-quadrilatères peuvent être non convexes – d’un point de vue affine – comme illustré ci-contre.
On voit aussi que le théorème de Varignon n’est bien entendu pas vrai mais que l’on pourrait chercher des cas particuliers de configurations où il pourrait être vérifié.
Lancer la figure de base contenant ces macros pour faire vos premières figures
Premières figures simples :
Pappus et Desargues
Exemple 1 – Configuration de Pappus
Les points \(A, B, C\) sont sur une droite, les points \(A_1, B_1, C_1\) sur une autre droite. On nomme \(M\) l’intersection des droites \((AB_1)\) et \((BA_1)\), puis \(N\) celle des droites \((AC_1)\) et \((CA_1)\), et \(P\) l’intersection de \((BC_1)\) et \((CB_1)\). Alors, dans le cas affine, les trois points \(M, N\) et \(P\) sont alignés.
C’est la propriété de Pappus qui aboutit à la commutatvité du corps des coordonnées (quand il existe bien entendu).
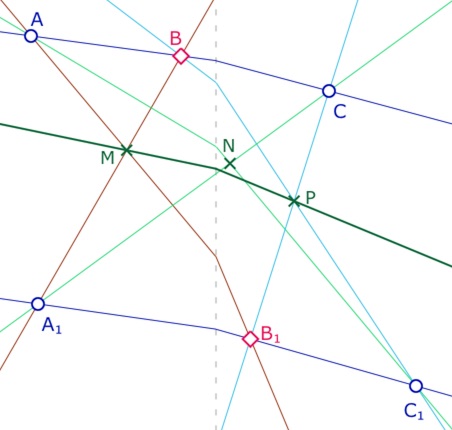
Dans le plan de Moulton, ce n’est, en général, pas le cas.
Ci-contre : cas de non alignement avec des droites \((AB)\) et \((A_1B_1)\) à pentes négatives.
Détail de construction :
\(B\) et \(B_1\) sont des points des droites \((AC)\) et \((A_1C_1)\) et donc nécessairement pris sur une des demi-droites qui composent les droites de Moulton.
Dans une figure plus aboutie, on pourrait, comme dans les figures du modèle de Hilbert, utiliser une poignée sur la droite euclidienne \((AC)\) pour guider un point \(B\) qui pourrait changer de demi-droite.
Exemple 2 – Réalisation de la configuration affine de Desargues
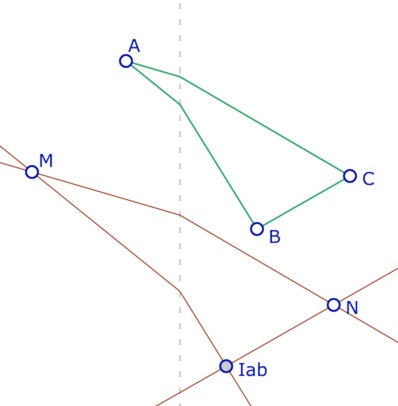
Étape 1 : on construit un triangle \(ABC\) (macro M-Segment) avec deux segments spécifiquement moultoniens.
Étape 2 : par un point \(M\) on prend les parallèles à \([AB]\) et \([AC]\). Prenant un point \(N\) sur la parallèle à \([AC]\) en le choisissant d’abscisse positive, on termine par la parallèle à \([BC]\) passant par \(N\).
Étape 3 : on prend alors l’intersection des deux parallèles. Bien entendu, même si la droite est à pente positive il faut montrer ses deux demi-droites. Cette macro produit le point d’intersection Iab que l’on renomme en \(P\).
Étape 4 : on termine la figure en traçant les trois M-droites \((AM), (BN)\) et \((CP)\). On illustre, ci-dessous à gauche, qu’en général ces trois droites ne sont pas concourantes : la configuration de Desargues n’est pas vérifiée, mais qu’il existe aussi beaucoup de situation où la propriété est vérifiées (à droite) – quand les trois droites issues de \(M\) sont à pentes négatives – comme conséquence du cas affine usuel.
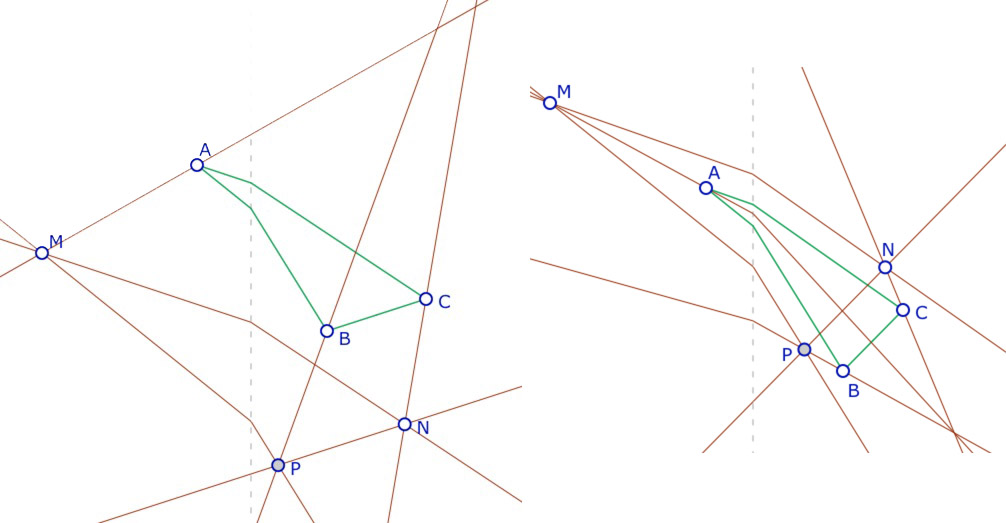
Dans ces deux figures, on a utilisé les macros M-droite ou M-segments, intersection de deux M-droites, ainsi que la construction de la M-parallèle à une droite. Nous allons maintenant utilisé le M-milieu
Constructions de figures
autour du concours des médianes
La macro M-Milieu
Elle doit fonctionner dans tous les cas, ce qui nécessite quelques précautions. Elle est ainsi rédigée, avec un double test. Les calculs sont élémentaires, il suffit de faire un dessin.

Version 1 : construction géométrique exacte
Tout d’abord on peut légèrement modifier la situation euclidienne pour construire un M-triangle avec un côté non euclidien et trois médianes euclidiennes classiques. On arrive alors facilement à une construction géométrique exacte qui montre clairement qu’un M-triangle peut avoir ses médianes concourantes. Voici une figure que l’on peut facilement reproduire.
Lancer la figure de base pour réaliser cette figure ou les suivantes
On peut aussi chercher, de manière plus heuristique – et donc, ici, de manière approchée – à illustrer la possibilité de M-triangles plus éloignés de la situation euclidienne, en particulier avec des M-médianes non euclidiennes.
Version 2 : les points A, B, C sont des points de base
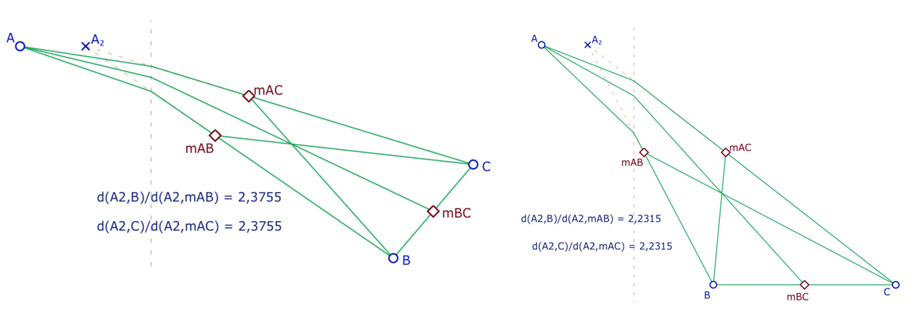
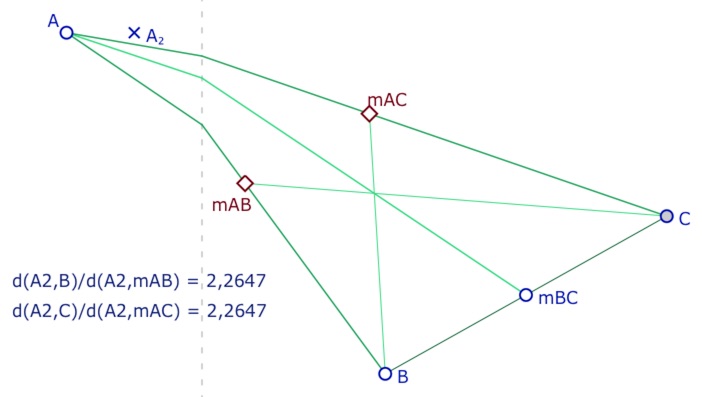
On construit un triangle \(ABC\) avec \(A\) d’abscisse négative et les deux côtés issus de \(A\) à pente négative. Alors la médiane issue de \(A\) est à pente négative. On note \(A_2\) le point de coordonnées \(\displaystyle \left( \frac{x_A}{2}, y_A \right)\). Dans le triangle \(A_2BC\), le milieu \(m_{BC}\) de \(B\) et \(C\) s’obtient par exemple avec le théorème du quadrilatère complet : si la droite des M-milieux \((m_{AB}m_{AC})\) est parallèle à \((BC)\), la droite passant par \(A_2\) et l’intersection des segments \([Bm_{AC}]\) et \([Cm_{AB}]\) coupe \((BC)\) en son milieu \(m_{BC}\). et donc les trois M-médianes de \(ABC\)sont concourantes.
Dans les deux illustrations ci-dessous, on illustre (à 4 décimales) le parallélisme de \((m_{AB}m_{AC})\) et de \((BC)\) par le rapport de Thalès dans le triangle \(A_2BC\). Pour cela on agit sur les trois sommets du triangle.
Remarque : l’argument ne tient que si les milieux \(m_{AB}\) et \(m_{AC}\) sont tous les deux d’abscisse positive.
Le commentaire du calcul des expressions
On rappelle que le texte avant la valeur numérique peut ne pas être le nom de la variable, mais un commentaire rédigé en deuxième ligne comme ci-dessous (ici recopie de l’expression elle-même).

Version 3 : avec comme points de base A, B, mBC
Ci-contre la même configuration que la précédente.
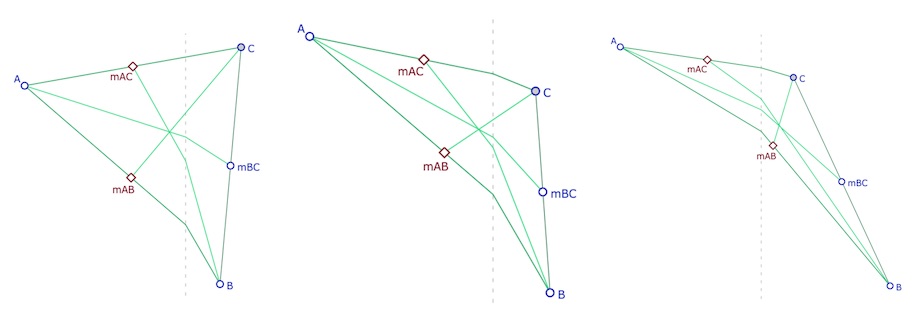
Ci dessous on peut explorer d’autres réalisations comme :
a – un coté et deux médianes à pentes négatives
b – deux côtés et deux médianes à pentes négatives (les deux milieux \(m_{AB}\) et \(m_{AC}\) sont à abscisses négatives)
c – idem que b mais avec un milieu à abscisse négative (\(m_{AC}\)) et l’autre à abscisse positive (\(m_{AC}\)).
Version 4 : avec trois médianes à pentes négatives
On peut aller un peu plus loin dans des triangles de Moulton plus éloignés de l’aspect euclidien, avec les trois médianes à pentes négatives.
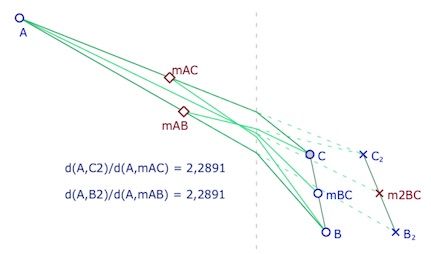
On retrouve l’argument du quadrilatère complet avec le triangle \(AB_2C_2\)où cette fois, \(B_2\) et \(C_2\) sont à abscisses double de celles de \(B\) et \(C\) respectivement, et non pas de moitié comme quand le cas où l’abscisse du point est négative comme précédemment.
Le parallélisme est à nouveau illustré (à 4 décimales) par les rapports de Thalès dans \(AB_2C_2\).
Version 5 : sans rapport avec le parallélisme d’une droite des milieux
Pour cette figure on utilisera la macro «M-droite avec origine» pour vérifier les alignements.\(A_2\) est aligné avec \(o_{AJ}\) et \(J\) par construction, mais ce n’est pas le cas de \(K_2\) avec \(o_{BK}\) et \(B\). Ici \(K_2\) est à la fois milieu de \(A_2\) et \(C_2\) et aussi le point \(\displaystyle \left( \frac{x_K}{2}, y_K \right)\).
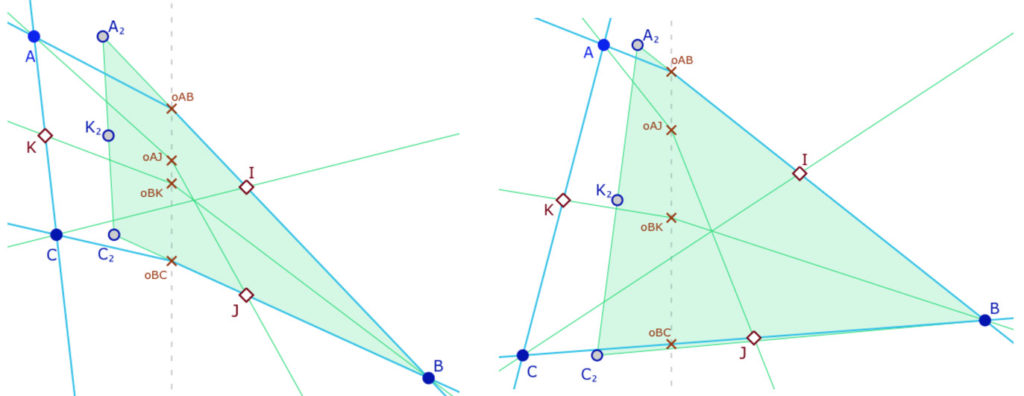
On voit bien que dans cette configuration, l’intersection des M-médianes ne peut être déduit d’aucune construction de médianes affines classiques comme déjà rencontré dans les exemples précédents. En particulier on peut avoir les médianes concourantes (ici de manière heuristique) sans que la droite des M-milieux \((IJ)\) ne soit parallèle, ni à \((A_2C_2)\) ni à \((AC)\).
Lancer la figure de base pour réaliser quelques unes ces figures.
Bien entendu, comme on a mené un calcul formel systématique sur les orthocentres des triangles de Moulton, on pourrait entreprendre le même travail pour les médianes , et construire des figures exactes. Ici, l’objectif était juste de proposer des variantes autour d’un thème pour réaliser des figures très rapidement.
Complément :
amélioration par programmation
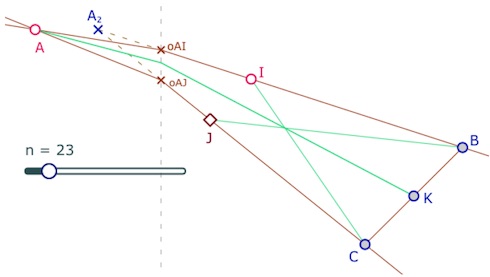
Dans la figure suivante, les points de base sont les points \(A, I\) et \(J\). \(B\) et \(C\) sont construits pour que \(I\) et \(J\) soient les milieux de \([AB]\) et \([AC]\). Comme dans les exemples précédents, les trois médianes sont concourantes si les droites \((IJ)\) et \((BC)\) sont parallèles. Mais au lieu de régler la figure à la souris, qui ne permet pas d’obtenir une précision au delà de \(10^{-4}\), on le fait par programme. On ajuste l’ordonnée de \(J\) pour que les rapports \(\displaystyle \frac{A_2C}{A_2J}\) et \(\displaystyle \frac{A_2B}{A_2I}\) soient égaux.
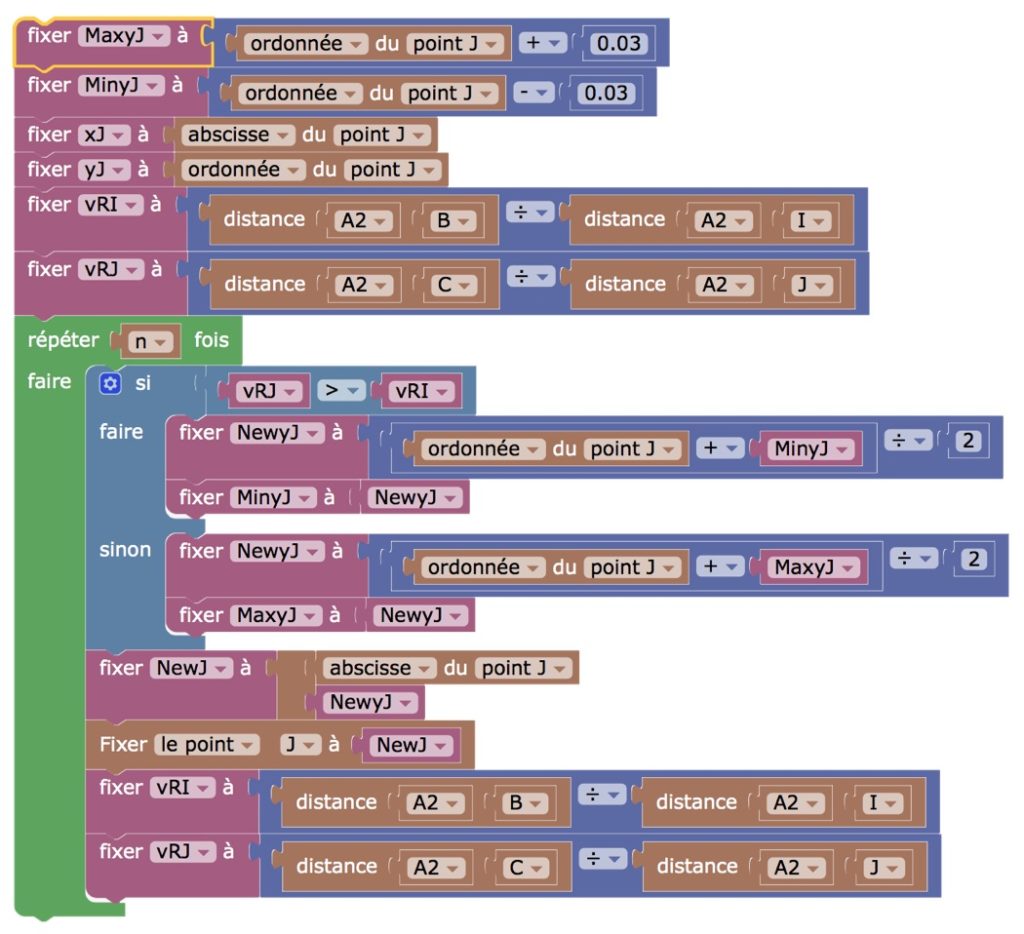
En pratique, dans la figure suivante, on vérifie que le programme égalise les rapports à 7 décimales, en agissant sur le curseur \(n\).
On peut aussi déplacer \(J\) en ajustant manuellement l’égalité des rapport à 3 décimales avant d’agir sur \(n\) pour activer le programme.
La figure est un peu grande, on propose de l’ouvrir dans un nouvel onglet.
Petit bonus : construire
les hauteurs d’un triangle
Parce que c’est trop sympa de construire soi-même les hauteurs d’un triangle, la figure suivante contient la macro des perpendiculaires. (Re)-voir la page dédiée dans le menu sur Moulton pour se remémorer le sens des parties rouge et verte. Il s’agit d’obtenir cela en quelques clics.
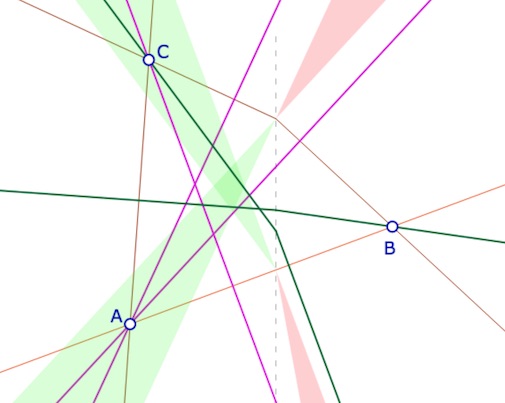
La macro M perp AB et M
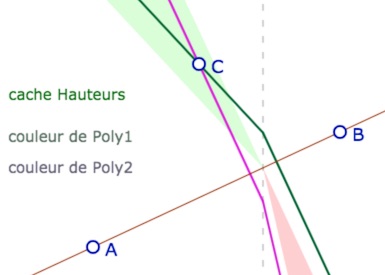
On montre simplement les points \(A\) et \(B\) de la droite dont on veut une perpendiculaire, et un point \(M\) d’où est issue cette perpendiculaire. La macro renvoie non seulement la – ou les deux – perpendiculaire(s) , les parties où il y a deux perpendiculaires (partie verte) et celle sans perpendiculaire (partie rouge), mais aussi trois expressions qui gèrent le tout et qui apparaissent sous les macros personnelles : il faut fermer les macros pour les voir. Il est conseillé, d’abord de les déplacer avant d’appliquer à nouveau la macro, et ensuite de les cacher avec la gomme.
Détail de comment sont construites ces perpendiculaires (dernière section de la page – assez technique … pas indispensale)
• Prendre 3 points et tracer les droites de Moulton, puis construire les trois hauteurs.
• Vérifier qu’u triangle peut avoir de 1 (minimum) à 5 (maximum) hauteurs.
• Retrouver des situations génériques où le triangle est « géométriquement » orthocentrique.
Préférer ouvrir cette nouvelle figure avec la macro M perp dans un nouvel onglet.